高炮弱相关射击误差的毁歼概率计算模型

姚志军， 谢杰涛， 赵志明， 郭治， 王军

(1.中国白城兵器试验中心, 吉林 白城 137001; 2.南京理工大学 自动化学院, 江苏 南京 210094)

0 引言

毁歼概率反映了高炮武器系统的整体性能，是最重要的战术技术指标之一。计算高炮毁歼概率的方法有实测统计法、模拟统计法和数学描述法。在武器系统定型试验中，出于安全性和费效比等因素考虑，不可能获得大量对真实目标的毁歼数据，实测统计法的应用从而失去了统计意义。模拟统计法也称Monte Carlo方法，其本质是用计算机模拟打靶，通过延长模拟时间和增加计算资源来获得足够多的数据，但是其正确性依赖于数据生成模型的正确性，主要用于模型验证和数据探索，业界尚不能接受用其计算结果作为定型依据。数学描述法通过对射击误差和毁歼机理进行分析，试图推导出毁歼概率的计算表达式，已成为学者们研究重点。

文献[1-4]和国家军用标准GJBZ 20499—98“高炮武器系统射击效率评定”[5]按时间相关性将高炮武器系统的随机误差分为强相关误差、弱相关误差和不相关误差3类，并认为这3类误差是彼此无关的正态过程。用d表示射击误差随机变量的维数(d=2为着发弹药，d=3为空炸弹药)，用n表示点射长度，则精确计算高炮点射的毁歼概率需要进行n×d重积分。若只考虑强相关误差和不相关误差，则只需要进行2d重积分，由此可见毁歼概率计算的复杂性主要是由弱相关误差引起的。如何处理弱相关误差，在保证计算准确性的同时降低计算复杂度，是数学描述法建模的关键问题。文献[1-4]中的误差平均法、相关系数最小二乘法和经验公式等误差模型转换法均试图将弱相关误差分解为强相关部分和不相关部分，并将前者与强相关误差合并为重复误差，将后者与不相关误差合并为不重复误差，进而给出毁歼概率计算的4重积分表达式。自从误差模型转换法中的误差平均法写入国家军用标准GJBZ 20499—98[5]后，这种分解方法几成定势，此后相关文献在涉及此内容时主要沿用结论，但这些方法均无法保持分解前后毁歼概率不变性，也不能给出结果的近似程度，因此长期以来靶场并不直接回答毁歼概率指标。文献[6]将平稳正态的射击误差序列分解为共有分量和非共有分量，将共有分量进一步分解为预测值和预测误差，虽然仍沿用弱相关分解的思路，但是已经试图引入现代控制理论的思想解决问题，不过文献[6]进行公式推导时只考虑了弱相关误差与初值的相关性，与弱相关误差状态方差不符。

本文从射击学基本假定出发，建立了弱相关误差序列的状态方程，采用严格的数学演绎，利用递推关系推导出命中概率的精确计算模型。给出了0-1毁伤定律毁歼概率计算模型，以方便与现有算法的比较。

1 弱相关误差序列状态方程

射击误差对着发弹药而言是迎弹面上的二维随机序列，对空炸弹药而言是空间三维随机序列，二者没有本质区别。本文采用一维形式进行分析，以方便地扩展到二维和三维形式。

记射击误差序列为{x(k)∈R;k=1,2,…,n}. 弱相关误差序列采用平稳正态过程模型进行描述，模型阶次由实际数据确定。为了与现行国家军用标准[5]体制保持一致，本文采用1阶平稳正态过程模型，状态方程如(1)式所示：

(1)

2 命中概率计算

记Ω为命中区域，则高炮n发点射的命中概率为

H(n)=1-P{x(1)∉Ω,x(2)∉Ω,…,x(n)∉Ω}.

(2)

由于各发炮弹之间具有相关性，(2)式对应的计算复杂度为n重积分运算。若要得到满足精度要求的结果，有必要进一步降低计算复杂度。

2.1 递推计算模型的推导

用g[x(1)]表示第1发弹目偏差的概率密度函数，则有

(3)

用g[x(k+1)]表示前k发炮弹均脱靶条件下，第k+1发弹目偏差的概率密度函数，f[x(k+1)|x(k)]表示已知第k发弹目偏差条件下第k+1发弹目偏差的概率密度函数，则有

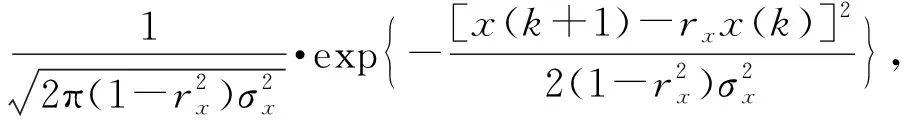
(4)

(5)

(6)

如图1所示，将脱靶区域沿坐标轴方向分成l个区域，{i}表示第i个区域。

用Pi(k)表示前k-1发炮弹均脱靶条件下第k发炮弹落在区域{i}的概率，则有

(7)

(8)

(9)

根据积分中值定理，有

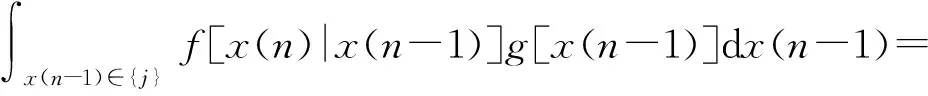
(10)

(11)

当‖i‖趋于0时，有

(12)

联立(8)式～(12)式，有

(13)

联立(2)式、(6)式、(13)式，有

(14)

分析(14)式可知，这是一个隐含的递推计算式，且系数与射击弹药序号无关。下面将进一步阐述这一结果。

2.2 计算模型的矩阵表示

用Pji(k+1)表示前k-1发炮弹均脱靶情况下第k发炮弹落在区间{j}、第k+1发炮弹落在区间{i}的转移概率，则有

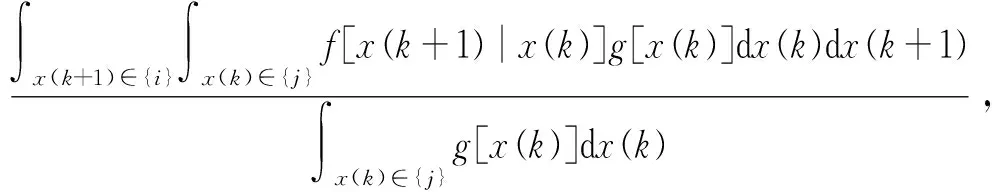
(15)

(16)

当‖i‖、‖j‖均趋于0时，联立(10)式～(12)式、(15)式，有

(17)

由(17)式可知，Pji(k+1)值与k无关，即Pji(k+1)=Pji，则有

(18)

令

(19)

P(k)=[P1(k),P2(k),…,Pl(k)]T，

(20)

则有

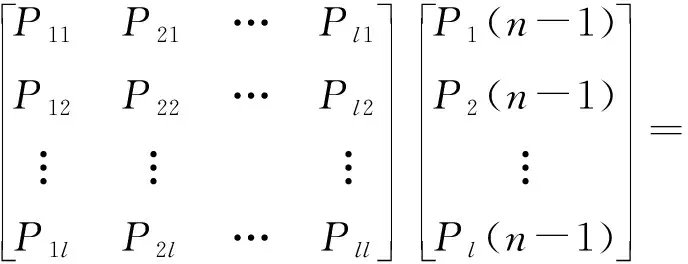
(21)

记l维单位向量e=[1,1,…,1]，有

H(n)=1-eAn-1P(1).

(22)

实际计算时，l只能取有限值。使用(22)式计算命中概率时，计算精度随着l的增大而提高。因此，可以通过比较增大l前后H(n)的值，确定H(n)的计算误差。用Hl(n)表示l为有限值时求得的毁歼概率，则H2l(n)对应的计算误差ΔH2l(n)满足：

ΔH2l(n)≤|H2l(n)-Hl(n)|.

(23)

(22)式只需要计算l+l2次一维积分，不需要进行n重积分运算。同时可以根据(23)式确定计算精度，满足了高精度计算的需要。

3 毁歼概率计算

从命中概率到毁歼概率，主要变化是引入了弹药对目标的毁伤能力，通常用毁伤定律来表征。对着发弹药而言，使用最广的是0-1毁伤定律和指数毁伤定律[2]。

0-1毁伤定律代表命中即毁歼，表示为

(24)

指数毁伤定律通常表示为

(25)

式中：ω表示毁歼目标所需的平均命中弹数，它反映了弹药威力和目标易损性。

指数毁伤定律的基本假定是：各发命中弹对目标毁伤是独立的，命中弹对目标毁伤没有累计效应[2]。在此假定下，确定威力的弹药对确定目标，其毁伤结果是确定且无后效的。如果将目标按易损性划分，则给定弹药对具体部位而言，要么能够毁伤，要么不能毁伤。即只要对目标划分足够细致，对具体某个划分的部位而言ω只有0和1两种取值，ω>1的部位均可以进行进一步划分，直至每部分ω的取值非0即1. 因此指数毁伤定律的本质仍旧是0-1毁伤定律。由于本文核心在于阐明毁歼概率递推模型的数学演绎过程，为了论述的简洁性，后续均采用0-1毁伤定律。

用Hk+1表示前k发炮弹均不毁歼条件下第k+1发炮弹毁歼概率，则

(26)

H1=1-eP(1)，

(27)

从而有n发炮弹点射的毁歼概率为

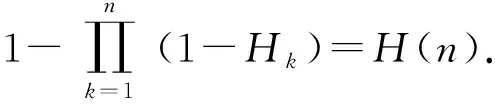
(28)

(28)式表明，对于0-1毁伤定律而言，点射的首次命中概率和毁歼概率是相等的。

4 与现有算法的比较

本文采用1阶平稳序列模型作为弱相关误差随机状态方程的基础，与包含国家军用标准在内的现有文献一致[2-5]，也可以采用高阶模型。采用0-1毁伤定律是为了比较方便，亦可以扩展到指数毁伤定律和坐标毁伤定律。下面通过计算示例，比较本文递推法、Monte Carlo法、误差平均法和相关系数最小二乘法。

Monte Carlo法的计算流程如下：对于每一次模拟实验，生成n个方差等于弱相关误差方差的白噪声；按照(1)式得出弱相关误差序列，逐发判断单发炮弹是否命中目标，统计命中弹数；按照(24)式或(25)式计算毁歼概率；重复这种模拟实验10万次，取毁歼概率平均值作为Monte Carlo法的计算结果。为了提高计算效率，可以一次生成n×106个方差等于弱相关误差方差的白噪声，每次模拟从中选取n个。

算例1在初始配置基础上改变rx，得到毁歼概率与相关系数的关系如图2所示。

从图2中可以看出，本文递推法与Monte Carlo法所得曲线几乎已经重合，从仿真角度佐证了递推法的正确性。可见误差平均法、相关系数最小二乘法计算结果偏大。4种算法在rx=1(相当于强相关误差)时结果一致；在rx=0(相当于不相关误差)时相差最大，本算例中毁歼概率结果差超过20%.

算例2设置身管数量p=1，重复算例1，得到结果如图3所示。

综合算例1和算例2可以看出，误差平均法和相关系数最小二乘法对于单身管高炮计算结果较为准确，但是仍与递推法有差距。分析原因可以发现，误差平均法和相关系数最小二乘法的计算结果有两部分误差：一是对弱相关误差进行近似分解产生的误差；二是将分解后的误差分量分别与不相关误差、强相关误差合并产生的误差。对于单身管武器系统而言，这两种方法都只有近似分解的误差，在合并部分不产生新的误差。但是对于多身管高炮而言，这两部分计算误差是同时存在的，弱相关误差近似分解后的不相关部分在同一时刻对于不同身管仍是相同的，而不相关误差在同一时刻对不同身管是独立的，相加合并的处理方式增加了不相关误差的比重，使毁歼概率结果偏大。

算例3在初始配置基础上设置p×n=24，改变p和n的值，得到毁歼概率与身管数量的关系如图4所示。

从图4中可以看出，误差平均法、相关系数最小二乘法和递推法的计算结果存在差异，且这种差异随着身管数量的增加而扩大。在用弹量一定情况下，高炮武器系统的毁歼概率随着身管数量的增加而下降，由于单身管射击频率一定，完成相同用弹量的用时减少，对特定的作战任务而言，通常要求在保证毁歼概率的前提下用时越短越好，因此武器系统身管数量的确定是毁歼概率和完成任务时间的综合权衡。

为了突出弱相关误差这一影响计算复杂度的主要因素，本文算例均忽略了系统均值、强相关误差和不相关误差。从计算结果可以看到，现有计算模型进行弱相关误差分解是有明显近似的，且这种近似是不可忽略的。

5 结论

本文建立了弱相关射击误差的随机状态方程，为利用现代控制理论解决射击学问题创造了条件；构造了连续脱靶条件下弱相关误差的概率密度函数，推导了命中概率的递推计算模型；采用0-1毁伤定律推导了毁歼概率的计算模型，其结果是精确的，可以作为现有计算模型的评价基准，亦可以扩展到指数毁伤定律和坐标毁伤定律；通过算例和现有毁伤概率计算方法进行了比较，说明包括国家军用标准在内的误差模型转换法均有明显偏差。

需要特别指出的是，本文给出的递推法正确性是在射击学基本假定前提下用严格的数学演绎所保证的，而非与Monte Carlo法一致性证明的，算例中本文方法与Monte Carlo法的高度一致只是本文方法正确性的一个佐证。事实上，在缺乏具有统计意义的实际射击结果的大前提下，由数学演绎保证正确性的本文方法是评价其他方法的基准。

参考文献(References)

[1] 潘承泮. 武器系统射击效力分析[M]. 北京: 国防工业出版社, 1985.

PAN Cheng-pan. Firing efficiency analysis of weapon system[M]. Beijing: National Defense Industry Press, 1985. (in Chinese)

[2] 潘承泮. 武器系统射击效力[M]. 北京: 兵器工业出版社, 1994.

PAN Cheng-pan. Firing efficiency of weapon system[M]. Beijing: Publishing House of Ordnance Industry, 1994. (in Chinese)

[3] 田棣华, 肖元星, 王向威, 等. 高射武器系统效能分析[M]. 北京: 国防工业出版社, 1991.

TIAN Di-hua, XIAO Yuan-xing, WANG Xiang-wei, et al. Efficiency analysis of anti-aircraft weapon system[M]. Beijing: National Defense Industry Press, 1991. (in Chinese)

[4] 罗兴柏, 刘国庆. 陆军武器系统作战效能分析[M]. 北京: 国防工业出版社, 2007.

LUO Xing-bai, LIU Guo-qing. Efficiency analysis of land force weapon system[M]. Beijing: National Defense Industry Press, 2007. (in Chinese)

[5] 中国人民解放军总参谋部炮兵装备技术研究所. GJBZ 20499—98 高炮武器系统射击效率评定[S]. 北京: 中国人民解放军总参谋部, 1998.

Institute of Artillery Equipment Technology, General Staff Department of the Chinese People’s Liberation Army. GJBZ 20499—98 Efficiency assessment of anti-aircraft weapon system[S]. Beijing: General Staff Department of the Chinese People’s Liberation Army, 1998. (in Chinese)

[6] 陶德进, 史慧敏, 王军, 等. 基于共有分量分解的速射火炮毁伤概率计算模型[J]. 兵工学报, 2012, 33(11) : 1358-1363.

TAO De-jin, SHI Hui-min, WANG Jun, et al. Damage probability calculation model of rapid-fire gun based on common component decomposition[J]. Acta Armamentarii, 2012, 33(11): 1358-1363.(in Chinese)