基于数值仿真的四种类型身管强度比较

杜中华

（军械工程学院，石家庄050003）

0 引言

枪炮身管在发射弹丸时要承受火药气体的高压，其所能承受的最高膛压即身管的强度。强度是身管的核心指标，枪炮的威力越大，要求身管的强度越高。目前身管已发展出了多种类型：最基础的是单筒身管；为了提高强度，发展出了筒紧、丝紧和自紧身管等增强身管；为了节约材料，发展出了可更换内衬的活动身管、活动衬管和短衬管等衬管身管[1-6]。各种身管结构上的差异导致其使用时在应力分布上存在不同，从而构成了不同的强度机理。

为了更好地理解不同类型身管的强度机理，这里选择有代表性的单筒、筒紧、衬管和自紧四种类型身管，借助数值仿真方法来比较分析它们的应力分布规律和强度机理，为枪炮身管设计提供参考。

1 四种类型身管强度理论[1-4]

为便于分析比较，四种类型身管采用同样的截面结构尺寸，如图1所示，内半径为a，外半径为b，筒紧和衬管身管的内外管分界半径、自紧身管的自紧半径为ρ，身管截面承受内压p1。材料采用理性弹塑性模型，如图2所示，忽略材料的应变强化和鲍辛格效应，内管和外管采用同样的材料，比例极限σp和屈服极限σs一致，材料的弹性模量为E。强度分析均采用第二强度理论，即最大应变理论：Eε≤σp。忽略较小的身管轴向应力σz。应力分布着重考察p和相当应力Eε，Eε最大值等于σp时身管内壁的p（p1）即身管强度P1。

图1 身管截面尺寸

图2 理想弹塑性模型

1.1 单筒身管

单筒身管结构简单，没有内外管之分。承受内压时身管发生弹性变形，相当应力中切向相当应力Eεt最大，依照厚壁圆筒理论有：

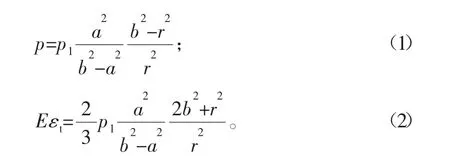
身管内壁处Eεt最大，令此处相当应力为σp，即得到单筒身管强度表达式

1.2 筒紧身管

筒紧身管是利用材料的热胀冷缩原理将外管热套在内管上，给内管一个径向压强p′2。内管和外管紧缩量之和与ρ的比值为相对紧缩量γ。

射击前，内管承受外压，外管承受内压，大小均为p2′；射击时，内外管作为整体承受内压p1，身管的应力分布就是这两种情况下的叠加。

筒紧身管的强度情况较为复杂，对于外管，Eεt最大；但是对于内管，可能Eεt最大，也可能最大，这和γ、p1以及结构尺寸有关。令各处最大的Eε均不超过σp的p1才是筒紧身管的强度。

1.3 衬管身管

衬管身管平时内管和外管之间有间隙e，射击时，首先内管承受压强并发生弹性变形，刚好能使间隙消失时承受的内压为间隙消失后，内管和外管作为整体承受内压身管应力分布为这两种情况下的叠加。

内筒内壁切向相当应力最大，据此得到身管强度

1.4 自紧身管

自紧身管承受内部高压，管壁部分发生塑性变形，在弹塑性交界处的压强

弹性区（ρ～b）：

塑性区（a～ρ），取泊松比为1/3：

自紧身管的强度即自紧压力，令式（14）中r=a，得

2 基于数值仿真的身管强度比较分析

以某型身管典型截面为对象，借助数值仿真方法对四种类型身管应力分布和强度进行比较分析。该截面a=50 mm，b=125 mm，ρ=75 mm，σp=σs=750 MPa，E=2.1×105MPa。

2.1 各型身管应力分布及强度分析

单筒身管切向相当应力Eεt分布如图3所示，为保证身管不致损坏，要求管壁内各处Eεt都不超过σp。由于内壁处Eεt最大，令该处Eεt与σp相等，此时对应的身管压力曲线如图4所示，内壁处的压力就是单筒身管的强度P1，此时身管强度为437.5 MPa。

图3 单筒身管切向相当应力

图4 单筒身管压力

取γ为0.001，筒紧身管相当应力分布如图5所示，可以看出，在内管，Eεt大于强度判定以Eεt为依据，当内管内壁Eεt刚好等于σp时，身管压力分布如图6所示，身管强度为531 MPa；取γ为0.002，筒紧身管相当应力分布如图7所示，可以看出，在内管，大于Eεt，强度判定以为依据，此时身管强度为587 MPa；γ为0.0025时，筒紧身管相当应力分布如图8所示，强度判定以外管Eεt为依据，此时身管强度为573 MPa。这里可以看出筒紧身管强度确定的复杂性。

图5 筒紧身管相当应力（γ=0.001）

图6 筒紧身管压力（γ=0.001）

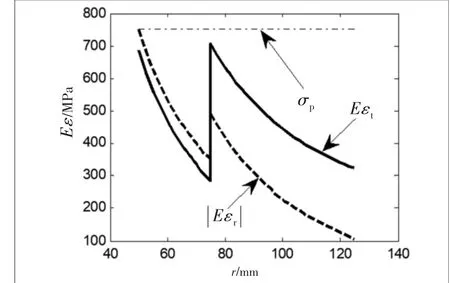
图7 筒紧身管相当应力（γ=0.002）

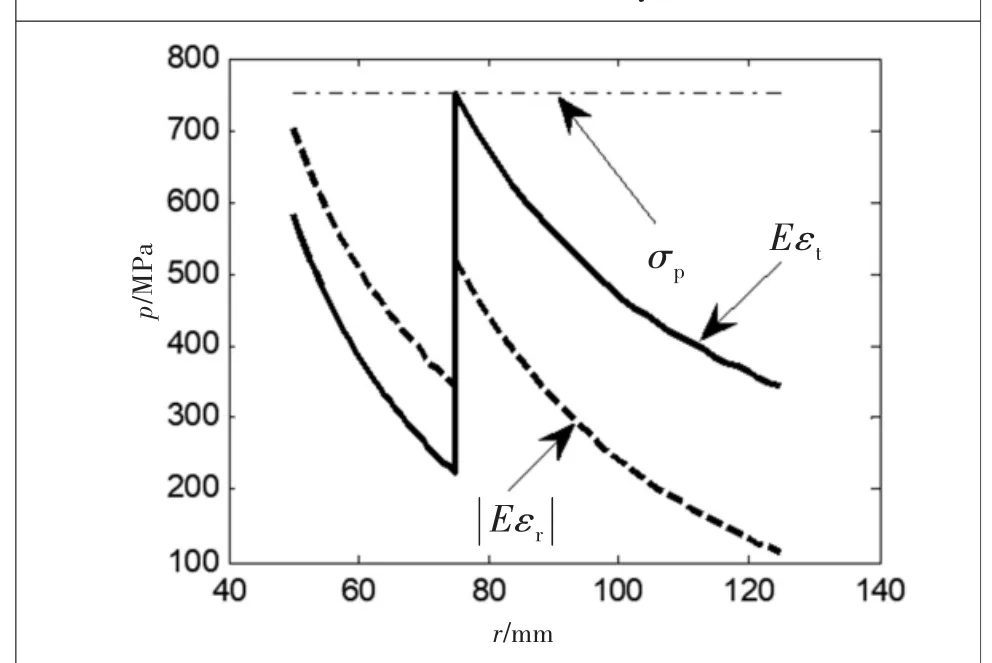
图8 筒紧身管相当应力（γ=0.0025）

取衬管身管内外管间隙e为0.075 mm，计算出衬管身管切向相当应力Eεt分布如图9所示。以Eεt为强度判据，当内管内壁Eεt等于σp时，得到身管强度P1为344MPa，如图10所示。

图9 衬管身管切向相当应力

图10 衬管身管压力

图11 自紧身管切向相当应力

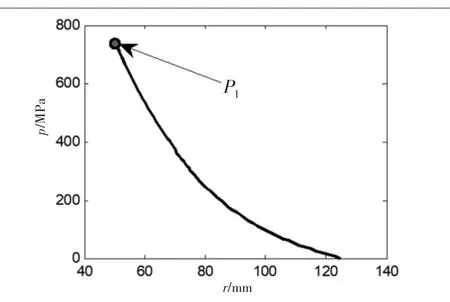
图12 自紧身管压力

当ρ=75 mm时（自紧身管自紧度为0.33），自紧时切向相当应力Eεt分布如图11所示，塑性区发生屈服，此时管壁内压力分布如图12所示，内壁处的压强即自紧压力，也是自紧身管的强度P1，这里为749 MPa。

由于采用第二强度理论，上面应力分析主要分析相当应力Eε和压力p，当Eε的最大值等于材料比例极限σp（或者σs）时，身管内壁处的压力即身管的强度P1。对于单筒、衬管和自紧身管来说，Eεt大于或者等于均以Eεt作为强度判据；筒紧身管情况较为复杂，强度判据可能是Eεt，也可能是

2.2 各型身管应力及强度比较分析

上面计算出衬管、单筒、筒紧、自紧身管的强度依次为344 MPa（e=0.075mm）、437.5 MPa、531 MPa（γ=0.001）、749 MPa，可知同样结构参数和材料参数情况下，身管强度依照上述身管类型顺序依次增大。

结构尺寸不变，筒紧身管γ取0.001（Eεt为强度判据），衬管身管间隙取0.075 mm，内压取300 MPa（四种类型身管强度足够，均不致破坏），四种类型身管的Eεt分布如图13所示。可以看出，Eεt的最大值，按照衬管、单筒、筒紧、自紧的顺序依次减小，以Eεt的最大值不大于σp（或者σs）为判据，也可以看出，身管强度按照上面顺序依次提高。

图13 身管切向相当应力比较

图14 身管强度随相对紧缩量变化曲线比较

取筒紧身管相对紧缩量γ从-0.002到0.0025变化，计算出身管强度如图14所示。当γ取负值、零和正值时，身管分别相当于衬管、单筒和筒紧身管。在γ小于0.00125时，身管强度P1随γ呈线性增加；在γ大于0.00125以后，P1随γ呈非线性变化，这主要是Eεt和大小关系发生了变化导致的。同样，取衬管身管间隙从正值到零到负值变化，身管强度也有类似的结果。这说明，通过内外管相对紧缩量或者间隙可以将衬管、单筒和筒紧这三种身管类型统一起来。

内压取500 MPa，筒紧身管γ取0.001时筒紧身管和自紧身管Eεt如图15所示。把筒紧身管内管沿半径均匀变为3个内管，各管之间γ均取0.001，则筒紧身管和自紧身管Eεt如图16所示，可以看出，在筒紧身管的内管部分，如果采用多层筒紧，其Eεt分布趋势接近自紧身管。这说明，自紧身管与多层筒紧身管一定程度上相类似。

3 结论

按照第二强度理论，身管最大相当应力Eε等于材料比例极限σp（或者屈服极限σs）时，身管内壁压强即身管强度。判定身管强度时，单筒、衬管、自紧身管只需考虑Eεt，筒紧身管则要考虑Eεt和

借助数值仿真方法，可以发现，同样结构参数和材料参数情况下，衬管、单筒、筒紧、自紧身管强度依次提高。借助筒紧身管相对紧缩量或者衬管身管间隙，可以将衬管、单筒和筒紧三种身管类型统一起来。自紧身管在一定程度上与多层筒紧身管类似。

目前关于枪炮身管强度的研究大都将身管类型分开，研究各自的应力分布和强度。本文关于多种类型身管应力和强度的比较研究为深入理解不同类型身管强度理论提供了依据，从而也为枪炮身管设计提供了参考。

图15 两种身管切向相当应力比较

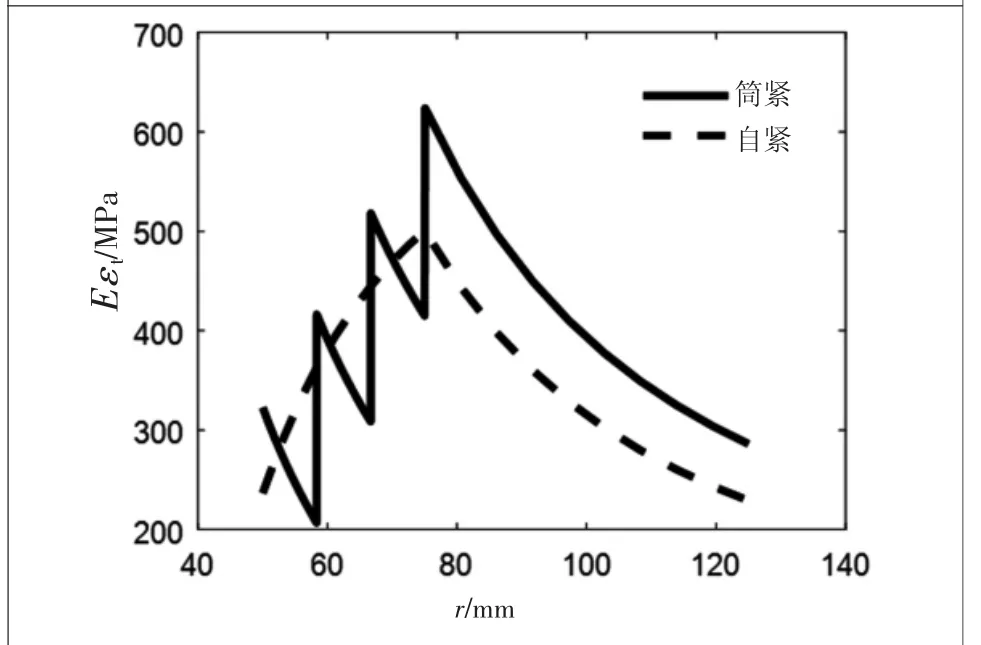
图16 两种身管切向相当应力比较

[1]潘玉田.炮身设计[M].北京:兵器工业出版社,2007.

[2]张相炎,郑建国,袁人枢.火炮设计理论[M].北京:北京理工大学出版社,2014.

[3]曾志银,张军岭,吴兴波.火炮身管强度设计理论[M].北京:国防工业出版社,2004.

[4]才鸿年,张玉诚,徐秉业,等.火炮身管自紧技术[M].北京:兵器工业出版社,1997.

[5]马福球,陈运生,朵英贤.火炮与自动武器[M].北京:北京理工大学出版社,2003.

[6]易声耀,张竞.自动武器原理与构造学[M].北京:国防工业出版社,2009.

[7]薛定宇,陈阳泉.基于MATLAB/Simulink的系统仿真技术与应用[M].北京:清华大学出版社,2002. （责任编辑 邵明涛）