衬里复合管全生命周期紧密度变化规律*
练章华 李泳宏 谷天平 牟易升 李 帅
(西南石油大学油气藏地质及开发工程国家重点实验室)
0 引 言
腐蚀是管道失效的主要原因之一,传统管材常因管道腐蚀造成巨大的经济损失和事故。管线的安全稳定性受到越来越多的关注[1]。双金属复合管的出现有效地减少了因管道腐蚀而造成的经济损失和事故。双金属复合管由碳钢基管和不锈钢衬管通过同轴装配液压胀接而成,其中基管主要起承压作用,衬管主要起耐蚀作用[2]。由于双金属复合管兼顾了经济性和耐腐蚀性的特点,在国内高腐蚀性油气田的集输过程中得到了大量应用,截至目前国内使用的双金属复合管管道累计超过1 500 km。
双金属复合管现有的API标准以及DNV标准都不完善,双金属衬里复合管液压成型后两管之间残余的结合强度是评价复合管结合质量的重要指标[3-4]。国内外学者对双金属的紧密度进行了大量研究。H.KRIPS等[5]最早提出了限制压力的概念并得到了胀管后基管与衬管间残余接触压力的解析解。王学生等[6]使用图解法,系统地研究了金属复合管液压胀接全过程,首次提出了当量屈服强度的概念,并建立了胀接力与接触强度——紧密度的计算模型,得出了紧密度与液压成型压力的计算公式。陈海云[7]依据图解法,将内层管材料屈服强度作为当量屈服强度,导出了金属复合管胀接后残余接触压力的解析式。A.R.AKISANYA等[8]利用弹性回复位移作为变形协调条件推导了残余接触压力。谢勇等[9]根据变形协调条件,得出复合管内外层残余接触压力与残余接触应力的正相关关系式。陈俊文等[10]研究了制管过程中复合管紧密度随内压的变化规律。由此可见,紧密度是评价双金属复合管结合质量的重要指标,分析紧密度的影响因素具有非常现实的意义。
双金属复合管的全生命周期包括制管、安装、运行以及停运。上述国内外学者的研究非常有价值,但大多只对双金属复合管成型过程的紧密度进行了研究,并未对双金属复合管运行过程中紧密度进行分析;特别是当衬里复合管处于运行工况时,温压耦合作用下的紧密度变化与管体应力分布还未研究。由于双金属复合管的基管和衬管材料不同导致其力学性质和热力学性质差异很大,使得温压耦合情况下基衬间接触面的相互作用非常复杂。为此,笔者建立双金属复合管的平面应变有限元模型,模拟双金属复合管从制管、安装、运行,到停运的紧密度变化与管体应力分布。研究结果对双金属复合管的研究及应用具有一定的参考价值。
1 衬里复合管紧密度力学理论
衬里复合管的制管工艺流程是将基管与衬管组合,通过在衬管内加压,使衬管与基管贴合产生接触,同时使衬管发生一定程度的塑性变形[11-12]。再经过泄压阶段,基管衬管的弹性模量不同,泄压后基管和衬管的弹性恢复程度也不同,基管的恢复程度大于衬管的恢复程度,这就会使基管衬管抱紧,从而产生一定的紧密度。
在复合管成型过程的公式推导中,假设衬管为线弹性强化材料模型,基管衬管复合时基管在弹性范围之内。复合管采用两端开式的自紧式密封结构,可忽略复合管的轴向受力情况,因此可按平面应力分析[13]。双金属复合管制管过程受力情况如图1所示。

图1 复合管成型过程中受力状态Fig.1 Force state of composite pipe during forming
复合管在制管时随着内压pi的增加,基管与衬管贴合产生接触压力pc。成型过程中衬管的受力情况如图1b所示。衬管外壁面的应力为:
(1)
式中:σθio为衬管外壁的径向应力,MPa;σrio为衬管外壁的周向应力,MPa;σsi为衬管的应变强化应力,MPa;k为衬管外径与内径之比。
根据广义胡克定律,衬管外壁的弹性应变为:
(2)
式中:εθio为衬管外壁的周向应变;E1为衬管的弹性模量,MPa;μi为衬管的泊松比。
复合管成型过程中基管的受力状况如图1c所示。基管内壁面的应力为:
(3)
式中:σroi为基管外壁的径向应力,MPa;σθoi为基管外壁的周向应力,MPa;Do为基管外径,mm;Di为基管内径,mm;K为基管外径与内径之比。
同理,基管内壁面周向弹性应变为:
(4)
式中:εθoi为基管内壁的周向应变;E2为基管的弹性模量,MPa;μo为基管的泊松比。
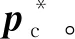
(5)
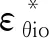

(6)
复合管受到运行压力p,此时复合管除了受到界面上的结合力p′外,还有基管给衬管的支撑力pc。同时,衬管外壁受到基管衬管之间的结合力p与基管对衬管的支撑力pc的作用,衬管内壁受到运行压力p的作用。基管的内壁受到基管衬管之间的结合力p′与基管对衬管的支撑力pc的作用[14]。
双金属复合管在运行阶段衬管应变表达式为:
(7)
式中:εri、εθi分别为内压作用下衬管的径向应变和周向应变;ν1为衬管材料的泊松比;tc为衬管的壁厚,mm;b为衬管外半径,mm。
将复合管衬管的应变分量表达式代入极坐标可得衬管在运行压力下的位移分量uri的表达式:
(8)
式中:uri为运行压力下衬管的径向位移,mm;r为衬管和基管结合面到管中心的距离,mm。
双金属复合管的基管为厚壁管在运行阶段受到支撑力与结合力的作用,根据极坐标中的几何方程和物理方程可得出其应变分量和径向位移式:
(9)
式中:εro、εθo分别为内压作用下基管的径向应变和周向应变;uro为内压作用下基管的径向位移,mm;c为基管外半径,mm;ν2为基管材料的泊松比。
假设运行阶段基管与衬管在界面上完全贴合,在运行压力作用下,基管和衬管的径向位移δ满足变形协调关系:
δ=(uro)r=b-(uri)r=b
(10)
将式(8)和式(9)代入式(10),可得运行压力p与紧密度(p′+pc)的关系式:
(11)
式中:a为衬管的内径,mm。
2 有限元力学模型的建立
以某油田常用的衬里复合管为例,其基管材料为管线钢X60,衬管材料为825镍基合金。
根据衬里复合管结构和制管过程的几何尺寸及边界条件等特点,结合弹塑性理论,数学建模时对材料塑性硬化部分进行了简化。双金属复合管的衬管需要达到塑性变形才能获得与基管内壁接触紧密度,在其液压膨胀和卸载过程中,可以获得较为准确的应力应变强化数据以及残余压力数据。由于复合管为中心对称模型,所以建立衬里复合管平面应变有限元模型,在模型上施加对称约束。模型中基管外径为323.8 mm、壁厚10 mm,衬管内径312.3 mm、壁厚3 mm。制管阶段,在衬管内壁上均匀施加31 MPa的胀接压力pi;运行阶段,再在衬管内壁分别施加0、8、14 MPa的运行压力pr;初始温度T0设置为常温20 ℃;运行阶段的复合管运行变化温度ΔT设置为 40 ℃。在停运阶段,将运行压力pr降至0。将复合管的衬管外壁与基管的内壁设置为接触对,并对衬管外壁与基管内壁接触界面周围的网格进行二次加密,来提高模型接触参数的计算精度。将基管内壁面作为目标面,将衬管外壁作为接触面,接触单元类型设置为target169单元和contact171单元,并使用增广拉格朗日接触求解方法。图2 为衬里复合管平面应变有限元模型。
通过调研获得不同温度下基管衬管的热力学参数,如表1所示。
温度是影响管道热膨胀力的主要原因。双金属复合管在制管、安装、运行、停运过程中温度有很大幅度的变化,并且双金属复合管运输的流体也具有很高的温度,而温度变化对基管和衬管的热膨胀系数及弹性模量都有很大的影响。但常用的分析方法在计算中仍然使用单一的材料力学参数,这就会导致温度变化时的计算误差。

图2 衬里复合管平面应变有限元模型Fig.2 plane strain finite element model of lined composite pipe

表1 基管衬管热力学参数表Table 1 Thermodynamic parameters of base pipe and lined pipe
3 双金属复合管全生命周期模拟及力学分析
3.1 双金属复合管全生命周期模拟
双金属复合管全生命周期包括复合管的制造、安装、运行以及停运。在双金属复合管生命周期中,温度与压力是影响的重要因素。图3是双金属复合管全生命周期的模拟流程图。在制造阶段,第1分析步(AB段)为加载,使衬管塑性变形与基管贴合,此时基管的最大应力为349 MPa,基管未发生塑性变形;第2到3分析步(BC段)是稳载,保持内压一段时间,使衬管充分膨胀与基管贴合,与实际制管过程相同,能有效提高计算精度;第4分析步(CD段)是复合管的卸载,用一个步长的时间线性卸载至0,在卸载后衬管的回弹量小于基管的回弹量,基管会抱紧衬管并产生紧密度。之后进入复合管的安装阶段,即第4到6分析步(DE段),在复合管的安装阶段复合管的温度达到最低温度0。第6到10分析步为复合管的运行阶段,包括管线加压(EF段)、管线稳压(FG段)、管线泄压(GH段),在此阶段复合管达到最高温度80 ℃。第10到12分析步(HI段)为复合管的停运。12个分析步包括了双金属复合管全生命周期的所有工况,以便于分析运行阶段温度与压力对复合管紧密度的影响。

图3 双金属复合管全生命周期的模拟流程图Fig.3 Simulation flow chart of bimetal composite pipe in the life cycle
双金属复合管在制管完成后,紧密度为0.839 MPa。在复合管的安装阶段达到最低温度0,此时双金属衬里复合管的紧密度为0.708 MPa。而在复合管的运行阶段,最高温度达到80 ℃时复合管的紧密度为1.231 MPa。停运后又恢复到制造完成后的紧密度。这说明复合管在安装、运行或停运极端工况中均具有较好紧密度;在高温运行停运后,其衬管和基管之间的紧密度又恢复到了制管后的紧密度,说明在设计工况下,复合管运行阶段的温度变化对双金属复合管的紧密度影响有限。
图4为不同运行压力下双金属复合管的全生命周期紧密度变化。本文模拟了3种不同工况下的双金属复合管的紧密度随加载步的变化。ab段为制管的增压阶段,紧密度从0增加到了24.26 MPa,说明随着内压增加基管发生塑性变形,开始与衬管接触紧密度逐渐增加。bc段为稳压阶段,接触压力不变。cd为泄压阶段,由于基管衬管材料不同,基管的回弹量比衬管的回弹量大,所以在泄压完成后基管与衬管之间仍然存在一定的残余接触压力,其值为0.874 3 MPa。当运行压力为0、温度为40 ℃时,紧密度逐渐增加到1.031 MPa。在运行工况下,运行压力为8 MPa、温度为40 ℃情况下,紧密度逐渐增加到7.231 MPa;运行压力为14 MPa、温度为40℃情况下,紧密度逐渐增加到11.543 MPa。
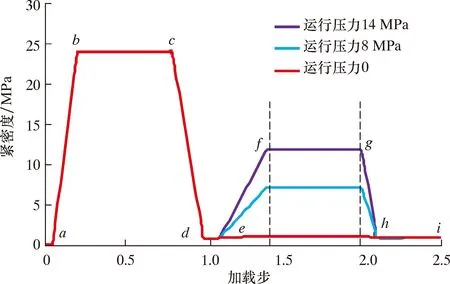
图4 不同运行压力下双金属复合管的全生命周期紧密度变化Fig.4 Change of tightness of bimetal composite pipe in the life cycle under different operation pressures
不同制管规格的复合管的紧密度同样随着运行压力的增加而增加,复合管在安装、运行以及停运工况下,运行压力对复合管的紧密度影响最大。在设计工况下,运行、停运后的复合管紧密度不变,即在设计工况下复合管不会因为温度与压力的变化而脱层。
3.2 双金属复合管全生命周期应力分析

图5 双金属复合管全生命周期的基管-衬管Mises应力云图Fig.5 Mises stress cloud chart of base pipe-lined pipe of bimetal composite pipe in the life cycle
提取图4中0~2.5分析步的双金属复合管全生命周期内的基管衬管的应力云图。图5 是双金属复合管全生命周期的基管-衬管Mises应力云图。图5a~图5d为双金属复合管的制管阶段。b点(图5a)状态是制管阶段Mises应力最大时刻,衬管的Mises应力为295.48~303.44 MPa;这时最小Mises应力已经超过了衬管的屈服强度,衬管发生塑性变形;此时基管上最大应力产生在基管内壁为359.16 MPa。d点(图5b)状态是制管阶段卸掉压力后的状态,随着内压的卸载,双金属复合管基管和衬管的紧密度不断减小。此状态下衬管的Mises应力范围在73.00~93.52 MPa,而基管应力在11.43~21.70MPa。当进入运行阶段,随着运行压力的出现,基管与衬管的应力均线性增加,并在f点达到峰值。e~h为运行阶段,在运行压力为0、8和14 MPa工况下(图5c、图5d、图5e),f点衬管的Mises应力范围分别为86.41~94.10 MPa、94.43~106.28 MPa、136.76~150.71 MPa,f点基管的应力范围分别为140.25~147.94 MPa、183.38~196.22 MPa、234.35~248.29 MPa。随着运行压力的逐渐减小直至为0,复合管进入停运阶段(图5f),此时基管的应力范围在11.43~21.69 MPa,衬管的应力范围在83.26~93.52 MPa。由此可知,运行压力对双金属复合管的基管-衬管的应力变化有很大影响,随着运行压力的升高双金属复合管基管衬管的Mises应力逐渐增加。
图6是双金属复合管全生命周期基管的Mises应力云图。由图6可知,在整个生命周期中,最大应力均位于基管内壁,最小应力均位于基管外壁。在制造阶段,基管的应力最大且最大应力位于基管内壁,最小应力位于基管外壁。在制造阶段,内压从0增加到31.5 MPa,此时基管的最大应力为359.16 MPa,最小应力为318.04 MPa。在泄压后进入到d点状态的最大应力为12.91 MPa。f点为运行阶段最大应力,在运行压力为0、8和14 MPa时基管最大应力分别为147.94、 196.23和248.29 MPa。i点为复合管的停运阶段,此时基管最大应力为12.91 MPa。

图6 双金属复合管全生命周期基管的Mises应力云图Fig.6 Mises stress cloud chart of base pipe of bimetal composite pipe in the life cycle
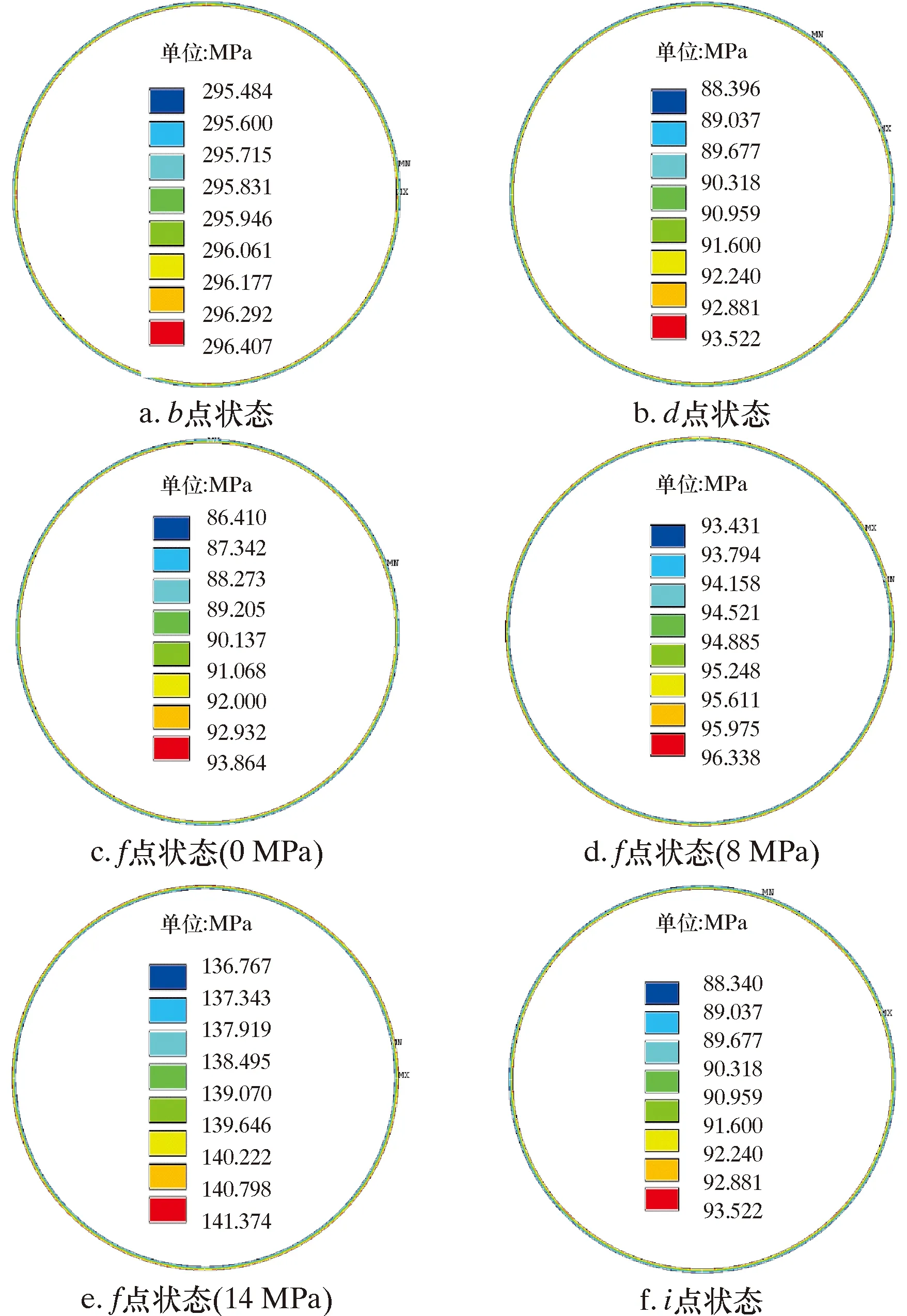
图7 复合管全生命周期中衬管的Mises应力云图Fig.7 Mises stress cloud chart of lined pipe of bimetal composite pipe in the life cycle
图7为复合管全生命周期中衬管的Mises应力云图。由图7可知,在复合管全生命周期中衬管的最大应力均出现在衬管内壁,最小应力均出现衬管外壁。b点衬管的最大应力为296.41 MPa;d点最大应力为93.52 MPa。当运行压力为0、8和14 MPa时,f点的最大应力分别为93.86、96.34和141.374 MPa。停运后i点最大应力为93.52 MPa。
在双金属复合管的全生命周期中,温度与运行压力是影响其紧密度的2个因素。在运行阶段温度对双金属复合管紧密度大小影响有限,但运行压力的大小会决定复合管衬管的变形程度,进而影响复合管的紧密度大小。因此,本文就运行压力对紧密度的影响进行了敏感性分析。通过改变运行阶段的运行压力,保持基管与衬管的材料性质不变,运行压力变化范围为0~14 MPa。运行压力与紧密度的关系曲线如图8所示。由图8可知,在复合管的弹塑性极限内,运行压力升高,衬管的塑性变形程度越大,与基管的贴合程度更好,复合管的紧密度也不断升高。
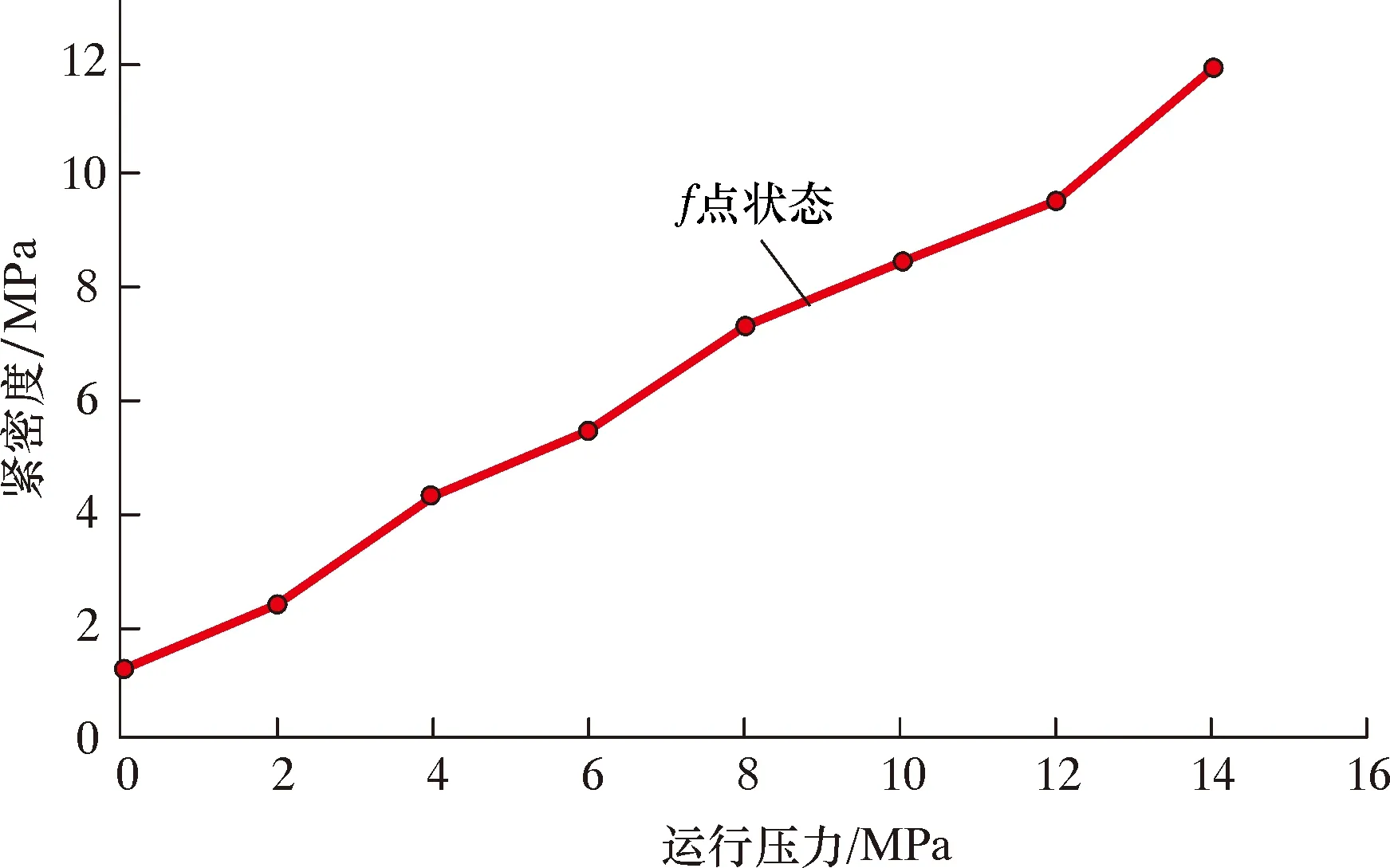
图8 紧密度随运行压力的变化曲线Fig.8 Change curve of tightness with the operation pressure
4 结 论
(2)双金属复合管制管、安装、运行过程中压力变化对复合管紧密度有很大影响。在3种不同运行压力工况下,双金属复合管的紧密度随着运行压力的增加而不断增加。当运行压力为0时紧密度最小为1.031 MPa,当运行压力为14 MPa时紧密度最大为11.93 MPa。因此适当增加运行压力有利于提高复合管的紧密度。而运行阶段在设计工况下,温度对复合管的紧密度影响有限,复合管不会发生脱层。
(3)在双金属复合管的全生命周期中,基管的最大应力位于基管内壁,最小应力位于基管外壁。在制造阶段衬管的最大应力出现在衬管内壁,最小应力出现在衬管外壁;在运行阶段衬管的最大应力位于衬管外壁,最小应力位于衬管内壁。且在双金属复合管的弹塑性极限内,基管和衬管的应力随运行压力的增大而增大。

