连续波钻井液脉冲器电流解耦控制器的研究*
闫宏亮 耿 焱 翟伟志
(西安石油大学电子工程学院)
0 引 言
随着世界上油气开发的难度越来越大,随钻测量技术对井下信息传输速率的要求也越来越高。连续波钻井液脉冲器作为钻井液脉冲随钻测量技术发展中的最新技术,是目前随钻测量数据钻井液脉冲传输系统的前沿发展方向[1]。
永磁同步电机(PMSM)作为连续波钻井液脉冲器转阀的驱动电机,其动态性能直接影响着井下信息传输的质量[2-4]。然而,PMSM受到井下温度变化的影响,其绕组阻值和电感会发生变化,使得电流环的耦合情况加强,若补偿不理想则会降低电机的动态性能。为了消除PMSM交、直轴之间的耦合,提高系统的动态性能,近年来,学者们在传统解耦控制的基础上,也做了很多研究。文献[5]将电感参数的变化和电压的误差作为系统的扰动,采用干扰观测器进行观测,并与偏差解耦控制相结合,实现了电流环的解耦控制。文献[6]在内模控制中引入了干扰观测器,观测电压误差和电机参数的变化,并对这些扰动进行补偿,实现了电流环的动态解耦控制。文献[7]针对静止同步补偿器电流的控制问题,提出了基于扩张状态观测器的解耦方案。文献[8]在内模解耦控制的基础上进行了改动,引入了滑模控制器,该方法提高了系统的鲁棒性。文献[9]改进了滑模观测器,并与复矢量解耦控制结合,实现了电流环的解耦控制。文献[10]主要针对电机的动态解耦,将电机参数的变化视为主要扰动,设计了新型龙贝格观测器,可以使系统得到完全补偿,实现电流环的精准控制。文献[11]利用电机本体的参考模型构造滑模面,设计速度观测器,以改善位置和速度估计精度,从而提高电机控制系统的鲁棒性。文献[12]为获得精确的电流观测值,通过低通滤波器滤除观测器输出的高频失真信号,实现了精准观测及电流环的解耦。文献[13]将未知测量噪声和外部扰动作用作为扩张状态变量进行观测,观测值可以有效补偿风电机组虚拟惯量,更好地抑制电网频率波动。文献[14]设计了一种基于1阶线性自抗扰控制的调速系统,线性扩张状态观测器可以对一般扰动进行估计,线性状态误差反馈控制律对扰动进行补偿,使磁链和转矩分量实现解耦控制。
上述文献虽然都实现了电流环的解耦控制,但均只将参数的变化作为扰动观测。而笔者提出的基于扩张状态观测器(ESO)的复合解耦控制,将定子电阻压降、交叉耦合项、内部不确定性干扰以及外部干扰均视为扰动,利用ESO进行实时观测和补偿,并与偏差解耦相结合,从而实现耦合项的补偿,达到动态解耦的目的。
1 传统电流解耦控制
1.1 数学模型
PMSM在d-q旋转坐标系中的定子侧电压方程如下:
(1)
式中:ud和uq分别表示d轴和q轴的电压;id和iq分别表示d轴和q轴的电流;Ld和Lq分别表示d轴和q轴的电感;R为电机的定子电阻;ψf为永磁体磁链;ωe为转子的电角速度;ωeLqiq和ωeLdid+ωeψf分别表示d轴和q轴的交叉耦合项。
通过式(1)可以得到,耦合项和转子的电角速度成正比,说明电机运行在高速状态下,交叉耦合会更加严重。
1.2 反馈解耦控制
本文选用的是id=0的控制方法。d-q轴交叉耦合项的补偿是本文研究的重点,所以笔者主要分析电流环调节器。
电流调节器采用传统的PI调节器,使用反馈解耦控制方法进行耦合补偿,通常由自动控制理论中的典型I系统对PI参数设计。但是该方法设计的参数鲁棒性较差,因此选用内模控制器对PI参数进行设计,并且内模控制器调节参数仅有1个[15],更加方便计算。当耦合被完全补偿消除后,d轴和q轴电流子系统就具有了统一的形式。以d轴为例,忽略延迟环节的影响,得到d轴电流子系统的闭环传递函数G(s)为:
(2)
式中:α′为调节参数;s为子系统电流。
画出α′从1 000到5 000变化时,d轴电流子系统的闭环传递函数的伯德图,如图1所示。从图1可以看到,当α′在1 000到5 000之间变化时,控制系统始终稳定。
1.3 偏差解耦控制
偏差解耦是从电流环给定值与反馈值处,引入外部的解耦支路,从而抵消掉耦合项的影响,实现系统的解耦控制。图2为等效的偏差解耦控制框图。

图1 d轴电流子系统闭环传递函数伯德图Fig.1 Bode diagram of closed-loop transfer function of d-axis current subsystem
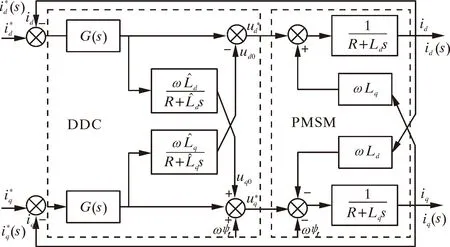
图2 等效偏差解耦结构图Fig.2 Equivalent deviation decoupling structure
由图2可以得到,电流给定值与反馈值之间的关系表达式如下:
(3)
其中:
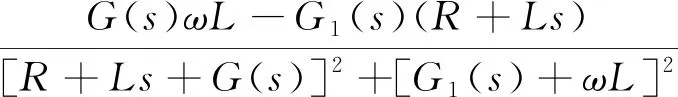
(4)
Cdd(s)=Cqq(s)=
(5)
(6)
2 基于ESO的复合解耦控制
2.1 ESO的控制原理
由于扰动是1阶系统,考虑将ESO设计为2阶,其表达式为:
(7)
其中:
(8)

2.2 ESO的设计
随着钻井深度的增加,脉冲器电机所处环境温度会上升,引起电机电感和电阻等参数变化,导致参数不匹配。本文将电机参数中的定子电阻R,d轴和q轴的电感Ld和Lq,内部不确定性干扰以及外部干扰均视为总扰动,用dd和dq表示,则有:
(9)
式中:ΔR、ΔLd、ΔLq和Δψf表示对应参数实际值和额定值之间的偏差量;εd和εq分别表示外部的扰动和等效未建模的部分。
对d轴和q轴分别设计对应的ESO,用fd和fq表示定子电阻压降、交叉耦合项以及干扰总和,将其视为总扰动。因为d轴和q轴的ESO具有统一的形式,则以d轴为例,式(7)可重新表示为:
(10)
其中:
(11)
将总扰动项作为系统扩张状态变量进行观测,为获取扩张状态变量的观测值,设计d轴的ESO为:
(12)
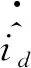
从式(12)可以看到,d轴ESO不受q轴干扰,两者观测器相互独立,互不干扰,有利于实现解耦控制。
2.3 基于ESO的复合解耦控制
将式(10)重新表示为:
(13)
其中:
(14)
在控制系统的设计中,将γd和γq分别作为d轴和q轴子系统中的干扰项,此干扰项由观测器观测并进行补偿。根据式(13)可以得到PMSM的简化模型。将其与扩张状态观测器相结合,可以得到PMSM的复合解耦简化结构图,如图3所示。
图3可用数学表达式描述为:
(15)
(16)

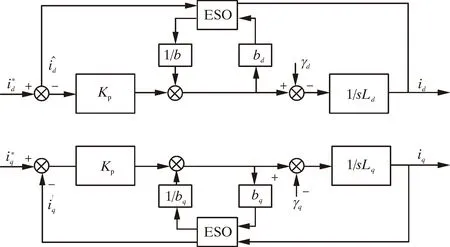
图3 基于ESO的PMSM复合解耦结构图Fig.3 Composite decoupling structure based on ESO
因为Kp>0,并且bd>0,所以闭环控制系统的输出可以跟踪输入,是收敛的,系统也稳定。
3 对比仿真分析
为了验证本文所采用的基于ESO的复合解耦控制策略的有效性和可行性,在MATLAB/Simulink中分别搭建了反馈控制解耦策略、偏差解耦控制策略以及复合解耦控制策略的模型,并且对这3种控制策略的d轴电流和转速波形图进行了对比分析。
模型中3种控制策略的转速环PI相同,其中比例系数为0.35,积分系数为50。PMSM参数为:rs=0.958 Ω,Ld=5.25 mH,Lq=12 mH,ψf=1.096 2 Wb。仿真电机突加突减负载运行情况如下,在0.2 s时由空载突加至满载,在0.3 s时由满载突减至空载,通过比较q轴电流变化时的d轴电流动态过程,从而反映3种控制策略电流环的动态解耦效果。
3.1 电机参数匹配时
电机的给定转速为1 000 r/min,在电机参数匹配的情况下使仿真电机突加、突减负载。图4为3种控制方法的d轴电流。通过波形可以看出:三者在电机参数匹配的情况下,电流子系统的解耦效果都很好,即在0.2和0.3 s系统负载值突变时,q轴电流的突变并未引起d轴电流的突变,d轴电流几乎没有波动,未受到q轴电流变化的影响。3种控制方法转速对比如图5所示。由图5可以看出,在电机加、减载的时候,3种控制策略的恢复时间几乎相同,其中反馈解耦的超调为0.9%,偏差解耦的超调为0.8%,复合解耦的超调为0.5%。可见复合解耦的动态速降最小,因此复合解耦的动态性能在三者中最好。

图4 电机参数匹配时3种控制方法的id对比图Fig.4 id vs.current for three control methods

图5 电机参数匹配时3种控制方法转速对比图 Fig.5 Rotary speed vs.time for three control methods
3.2 电机参数不匹配时
3.2.1 电感参数不匹配

图6 3种控制方法id对比图(电感不匹配)Fig.6 id vs.current for three control methods (mismatch of inductance)
当外界原因导致电机所处环境温度升高时,会导致电感的阻值变小。当电机参数电感的实际值为额定值的0.7倍时,电机的给定转速仍为1 000 r/min,电机突加、减载。 图6为3种控制方法的d轴电流。由图6可以看出:在0.2 和0.3 s系统突加、减载引起q轴电流突变时,反馈解耦控制的d轴电流具有很明显的波动;偏差解耦控制的d轴电流也具有一定程度上的波动,但是波动的幅值要比反馈解耦控制的小很多;复合解耦控制中,d轴的电流几乎不变,保持一条直线,未受到q轴电流的影响。3种控制方法转速对比如图7所示。从图7可以看出,3种解耦方式的恢复时间几乎一致,其中反馈解耦的超调为1.1%,偏差解耦的超调为0.9%,复合解耦的超调为0.5%。可见复合解耦的动态速降最小,因此复合解耦的动态性能在三者中最好。

图7 3种控制方法转速对比图(电感不匹配)Fig.7 Rotary speed vs.time for three control methods(mismatch of inductance)
3.2.2 电阻参数不匹配时
当外界原因导致电机所处环境温度升高时,会导致电阻的阻值变大。当电机电阻的实际值为额定值的1.5倍时,电机的给定转速为1 000 r/min,电机突然加载和减载。图8为3种控制策略下d轴波形图。

图8 3种控制方法id对比图(电阻不匹配)Fig.8 id vs.current for three control methods (mismatch of resistance)
由图8可以看出:在0.2和0.3 s时,反馈解耦控制的d轴电流受到了q轴电流变化的影响,有明显波动起伏,解耦效果不理想;偏差解耦控制的d轴电流基本保持一条直线,但是电流整体的波形不是很平滑,说明电流在0附近,跳跃比较大;而复合解耦控制的电流波形几乎没有波动,电流波形也很平滑,解耦效果更好。图9为3种控制方法转速对比图。由图9可以看出,3种解耦方式的恢复时间几乎一致,其中反馈解耦的超调为1.35%,偏差解耦的超调为1.15%,复合解耦的超调为0.50%。可见复合解耦的动态速降最小,因此复合解耦的动态性能在三者中最好。
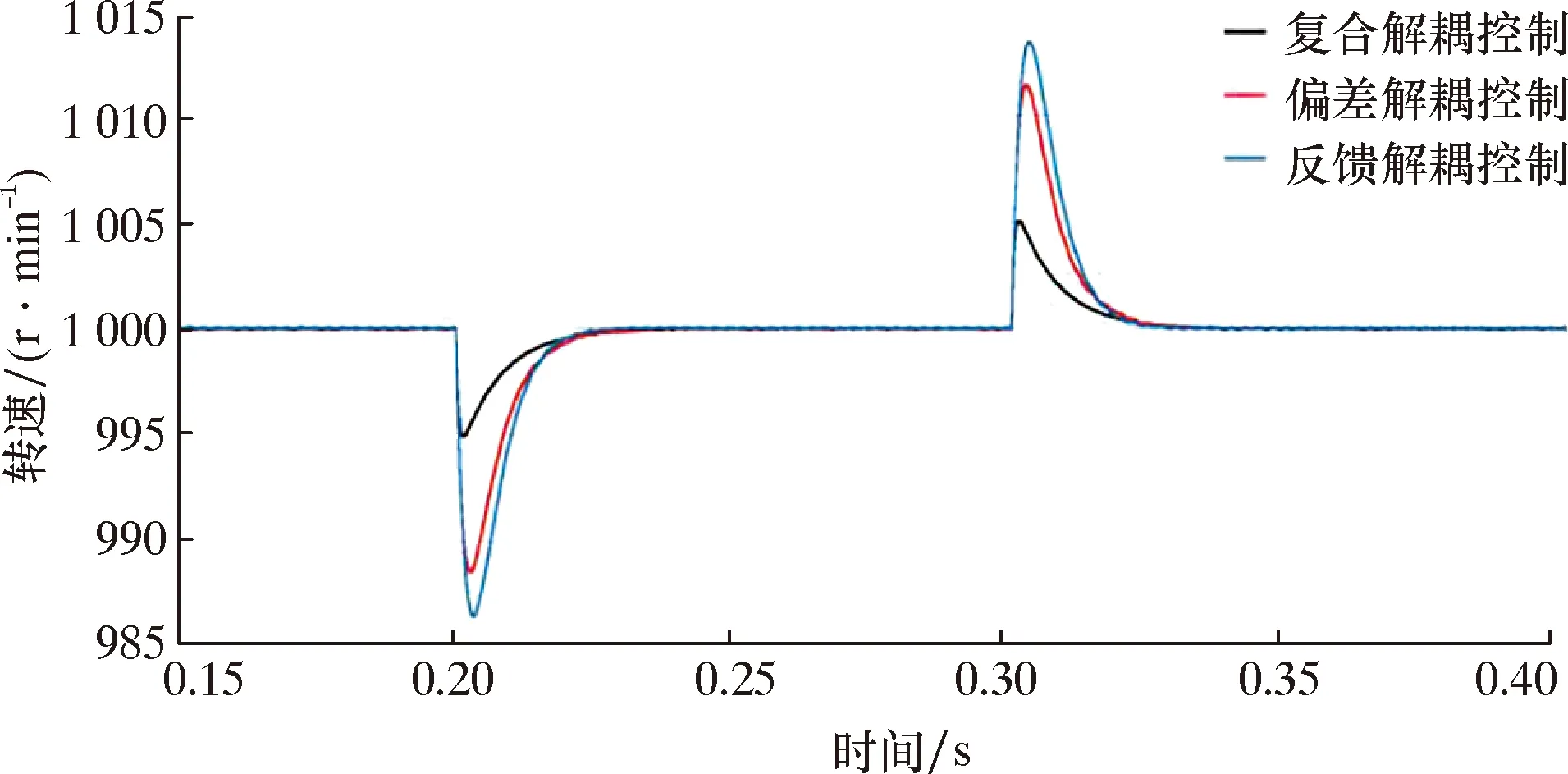
图9 3种控制方法转速对比图(电阻不匹配)Fig.9 Rotary speed vs.time for three control methods (mismatch of electrical resistance)
4 结 论
(1)在电机参数匹配时,反馈解耦控制和偏差解耦控制具有相同的动态性能,复合解耦控制的动态性能优于前两者;3种控制方法均可补偿电流子系统的耦合项,复合解耦控制在抗负载扰动性能上也是三者中动态速降最小、性能最好的。
(2)在电机参数不匹配时,无论是电感参数还是电阻参数不匹配的情况,反馈解耦控制和偏差解耦控制均不能完全实现电流环的动态解耦,在突加、突减负载时,d轴电流均出现了不同程度的波动,并且转速的动态速降增大,整个控制系统的抗负载扰动性能也出现了波动。但是复合解耦控制在相同条件下,完全实现了电流环的动态解耦,并且此时的动态速降和参数匹配时相同,并没有因为参数的变化使得电机转速的超调增大,明显提高了系统的抗扰性能和鲁棒性。
(3)将复合解耦应用在连续波钻井液脉冲器转阀驱动电机的电流环控制中,可以提高电机控制系统的动态性能,从而提高连续波钻井液脉冲器的信息传输质量。

