基于钻头-岩石互作用的减振器应用效果分析*
0 引 言
钻井是一个非常复杂的动态过程,在这个过程中,由于钻头牙齿与井底岩石、钻柱与井壁之间接触的非线性,以及井底形状的动态随机性,使得下部钻具的运动和受力情况十分复杂,振动不可避免,在遇到硬度较大且稳固性较低的岩层时振动尤为剧烈[1-2]。为抑制钻具振动,较为通用的做法是井下安装钻具减振器。
针对井下钻具的振动特性及减振器的应用效果,国内外学者开展了大量的研究工作。F.CLAYER等[1-3]研究了地面和井底边界条件对井下钻具振动特性的影响,指出井底边界条件较为复杂,受地层性质、转速和钻压的影响,难以用准确的时间历程函数来表达钻具的振动响应。T.G.RITTO等[4]建立了井下钻具非线性动力学模型,发现钻头和岩石的随机互作用对钻具系统的振动响应具有较大的影响,指出分析钻柱动力学必须考虑钻头和岩石的相互作用。M.E.WASSELL等[5-6]研究了减振器刚度和阻尼等参数对钻柱纵横耦合振动的影响,指出减振器并非都能提高机械钻速。张晓东等[7]将井下钻具简化为一个七自由度系统,采用激励位移的方式,分析了不同安装位置的减振器的减振能力,指出减振器最优安装位置受钻头转速影响。王文龙等[8-9]建立了井下钻具纵向和扭转振动的数学模型,发现采用不同井底边界条件时,井下钻具振动和减振器减振效果存在很大差异,甚至截然相反,提出应采用激励位移法来研究钻具纵向振动,激励转角法来研究钻具的扭转振动。王建龙等[10]针对钻井过程中跳钻剧烈及钻头磨损严重的难题,设计了地面可视化减振器,有效提高了机械转速,延长了钻头使用寿命。董广建等[11]研究了钻柱振动和冲击的表现形式,指出在钻柱动力学研究过程中需要充分考虑井下实际情况,尽量建立接近真实环境的模型,减振器设计应用时,需要充分分析减振器性能参数、数量和位置,以提高使用效果。祝效华等[12]建立了三维井眼钻柱-钻头-岩石系统动力学模型,分析了钻具非线性纵/横/扭耦合振动。YANG C.X.等[13]研究了钻柱纵向振动特性,指出钻柱纵向振动是井下钻柱疲劳失效的直接原因,分析结果表明,在匀速钻进过程中,纵向振动可以被视为一种随机振动。刘静等[14]研究了井下钻柱在横向、纵向和扭转方向上的耦合振动问题,建立了井下段钻柱非线性耦合振动数学模型,分析了钻压、转速对钻柱耦合振动及钻井液压力波动的影响。
随着理论研究和井下测试技术的发展,井下钻具振动的非线性和随机性已基本成为业内共识。在钻头钻进过程中,无论是位移激励还是力激励都难以真实反映钻头在井底的受力和运动情况,基于这2种激励方式来研究减振器的应用效果,分析结果与实际存在较大差异。目前尚无以钻头破岩钻进为井下边界条件研究减振器应用效果的文献公开发表。为此,笔者在考虑钻头、岩石随机接触以及钻柱-钻头-岩石系统动力耦合的基础上,研究了减振器及其关键参数对下部钻具纵向振动的影响,以期为钻柱振动控制和减振器现场应用提供参考。
1 模型描述
1.1 基本假设
由于剧烈振动往往发生在近钻头的下部钻具,考虑到本文的研究重点为减振器对其上端钻柱和下端钻头振动特性的影响,为便于分析并减少计算量,做出如下基本假设:
(1)下部钻具为均质空间弹性梁,忽略接头螺纹和孔槽结构;
(2)钻具上端边界简化为恒定的上提力和转速;
(3)钻头端以钻头与岩石互作用作为边界条件,岩石破坏后删除;
(4)由于钻头强度和刚度远大于岩石,所以将钻头各牙轮和牙齿简化为刚体。
1.2 力学模型
井下钻具受力情况如图1所示。其中:FT为钻具上端上提力,N为转速,p为井底岩石围压,T为钻压。
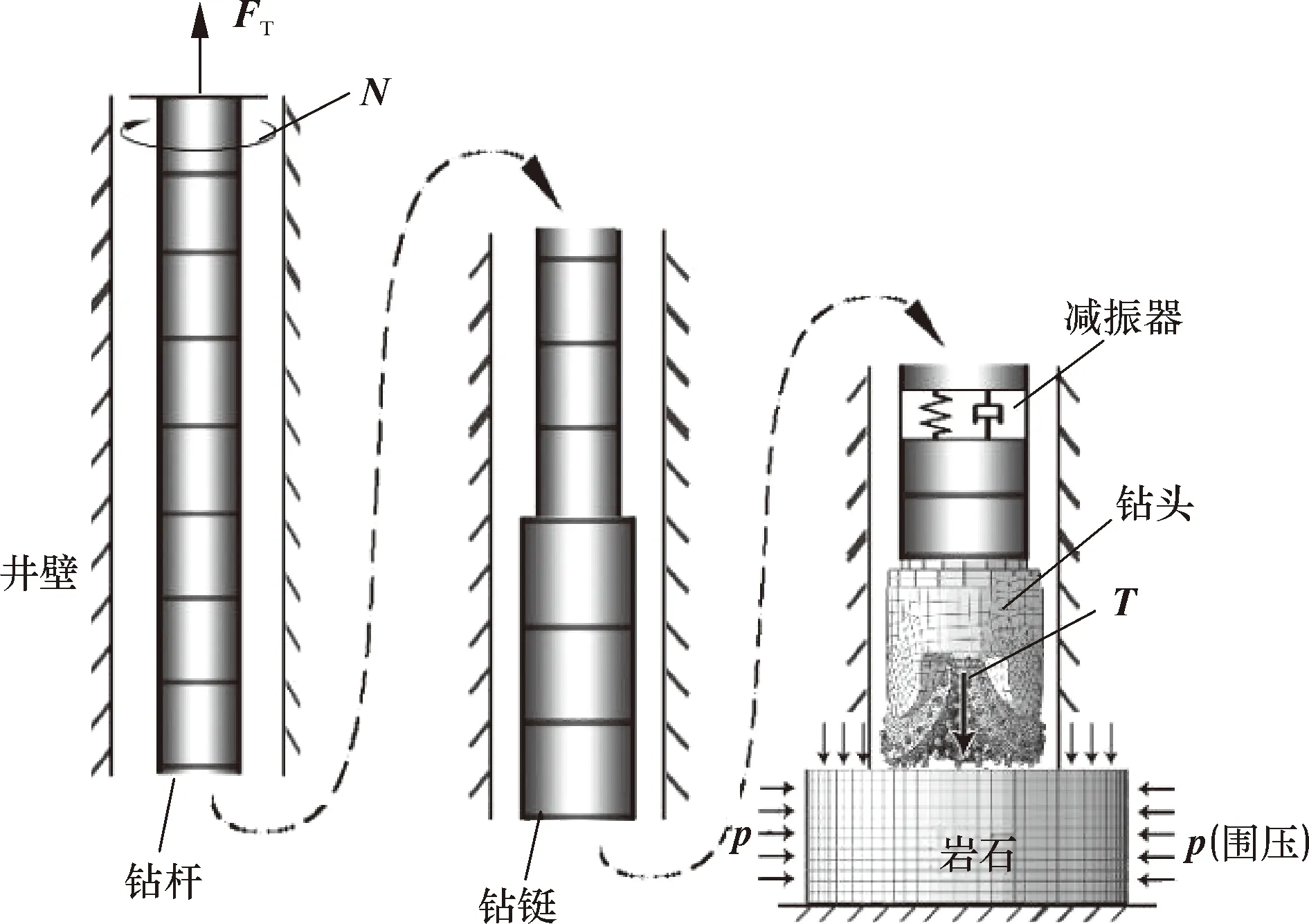
图1 系统力学模型Fig.1 Mechanical model of system
根据虚功原理,钻柱-钻头-岩石系统符合非线性动力平衡基本方程:

(1)

考虑到钻头与岩石、钻具与井壁接触的随机性以及岩石材料的非线性,采用有限元法求解,其中钻杆、钻铤采用三维梁单元,钻头为刚体壳单元,岩石采用六面体实体单元。为提高计算精度,对钻头牙齿和岩石接触区域进行了网格细化,计算模型和求解过程详见文献[15]。
2 参数设置
钻井参数:转速N=100 r/min,钻压T=60 kN;钻井流体为空气,黏度2×10-5Pa·s;
钻具组合:ø216 mm三牙轮钻头+ø215 mm稳定器×1.45 m+ø178 mm钻铤×27.35 m+ø159 mm钻铤×44.35 m+ø127 mm钻杆;
钻头结构参数:外径216 mm,轴颈角57°,移轴距7 mm;
井眼直径:230 mm。
岩石本构关系采用Drucker-Prager模型[16],其主要力学参数:弹性模量为51.5 GPa,泊松比为0.33,内摩擦角为30.16°,抗压强度为120 MPa,围压为30 MPa。
3 结果与分析
3.1 钻头和钻柱振动强度分析
图2和图3分别为钻头和中和点处钻柱(距钻头40 m)的振动情况。从图2和图3可以看出:钻头钻压和钻柱纵向力、速度的变化具有明显的随机性和非线性,其中钻头钻压波动范围为17~158 kN,平均振幅(均方差,下同)21.5 kN;速度波动范围为-86~112 mm/s,平均振幅41.2 mm/s。受井下阻尼的影响,钻柱振动强度略低于钻头,其纵向力范围为-51~62 kN,平均振幅20.2 kN;纵向速度范围-92~121 mm/s,平均振幅39.7 mm/s。

图2 钻头钻压和钻柱纵向力响应曲线Fig.2 Response curves of WOB and drill string longitudinal force

图3 钻头和钻柱速度响应曲线Fig.3 Velocity response curves of bit and drill string
3.2 减振器应用效果分析
减振器的作用主要体现在以下2个方面:一是改变井底激励条件,即改变钻头与岩石互作用过程中的受力和运动情况;二是隔断减振器上下两端钻具的动力耦合,即减小钻头动载对上端钻柱的影响。
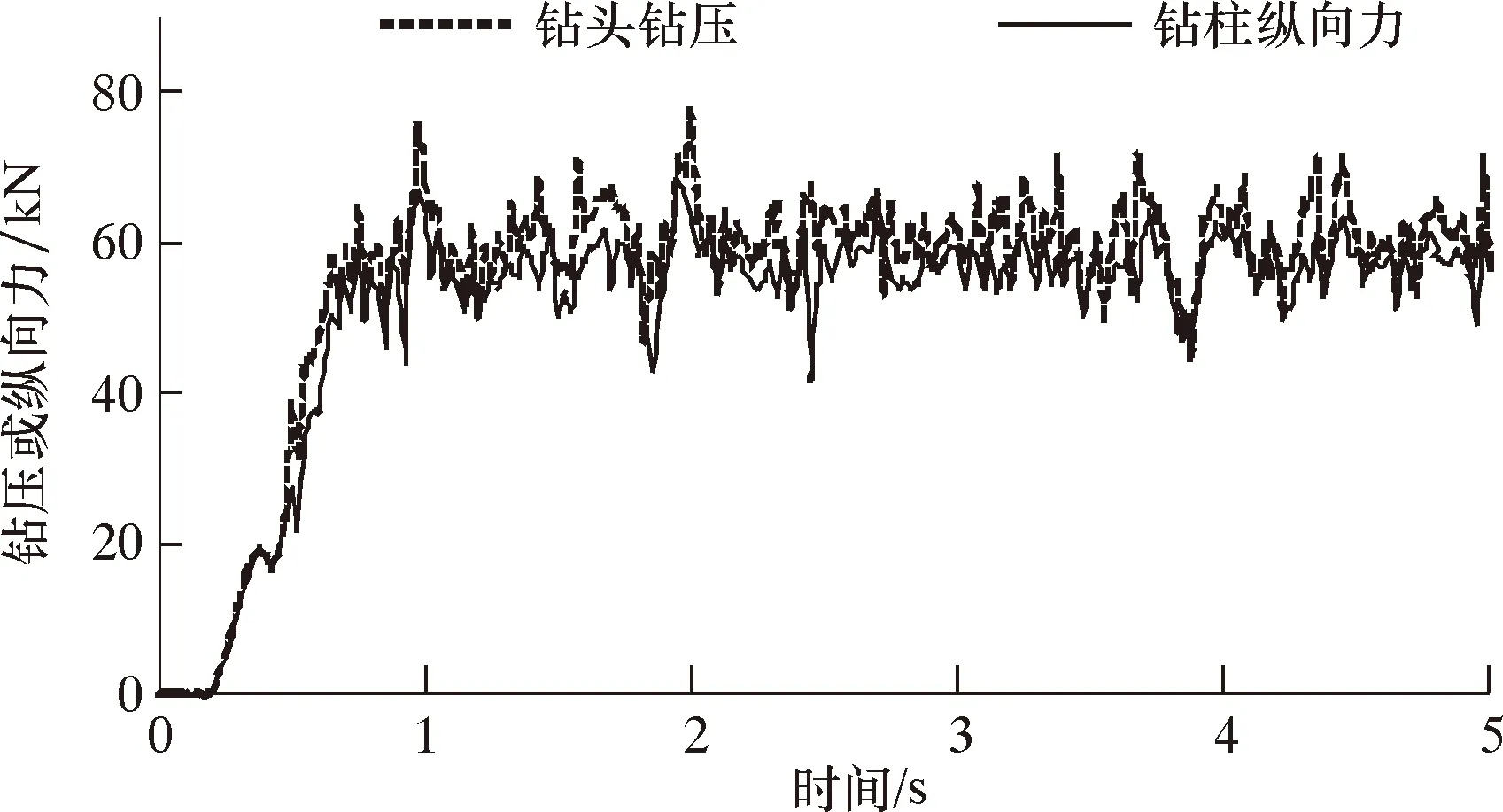
图4 应用减振器后钻头钻压和钻柱纵向力响应曲线Fig.4 Response curves of WOB and drill string longitudinal force after application of shock absorber
保持其他参数不变,在钻具中加入减振器,减振器刚度5.5 kN/mm,阻尼80 N·s/mm,距钻头1 m,分别取减振器下端钻头和上端钻柱(距钻头2 m)的动力学特性,结果如图4和图5所示。从图4和图5可以看出:使用减振器后,钻头和钻柱振动强度大幅度降低,钻压为48~78 kN,平均振幅4.1 kN,同未使用减振器相比,降低了81%;减振器上端钻柱纵向力范围为42~68 kN,平均振幅3.1 kN,比钻头处降低了24%;钻头纵向速度范围-149~224 mm/s,平均振幅41.6 mm/s,与未使用减振器时基本一致;钻柱纵向振动速度范围-36~52.8 mm/s,平均振幅13.3 mm/s,比钻头处降低了68%。
综上所述,减振器对其上端钻柱和下端钻头的受力和运动特性的影响存在差异:应用减振器后,减振器上端钻柱的纵向力和速度平均振幅均降低;减振器下方钻头钻压平均振幅大幅度降低,但其振动速度变化不大。其原因主要在于减振器使钻头上方钻具的纵向刚度降低,在受到岩石反作用力时,钻头更容易发生纵向运动,因而出现了受力的大幅度降低但振动速度变化不大的情况。
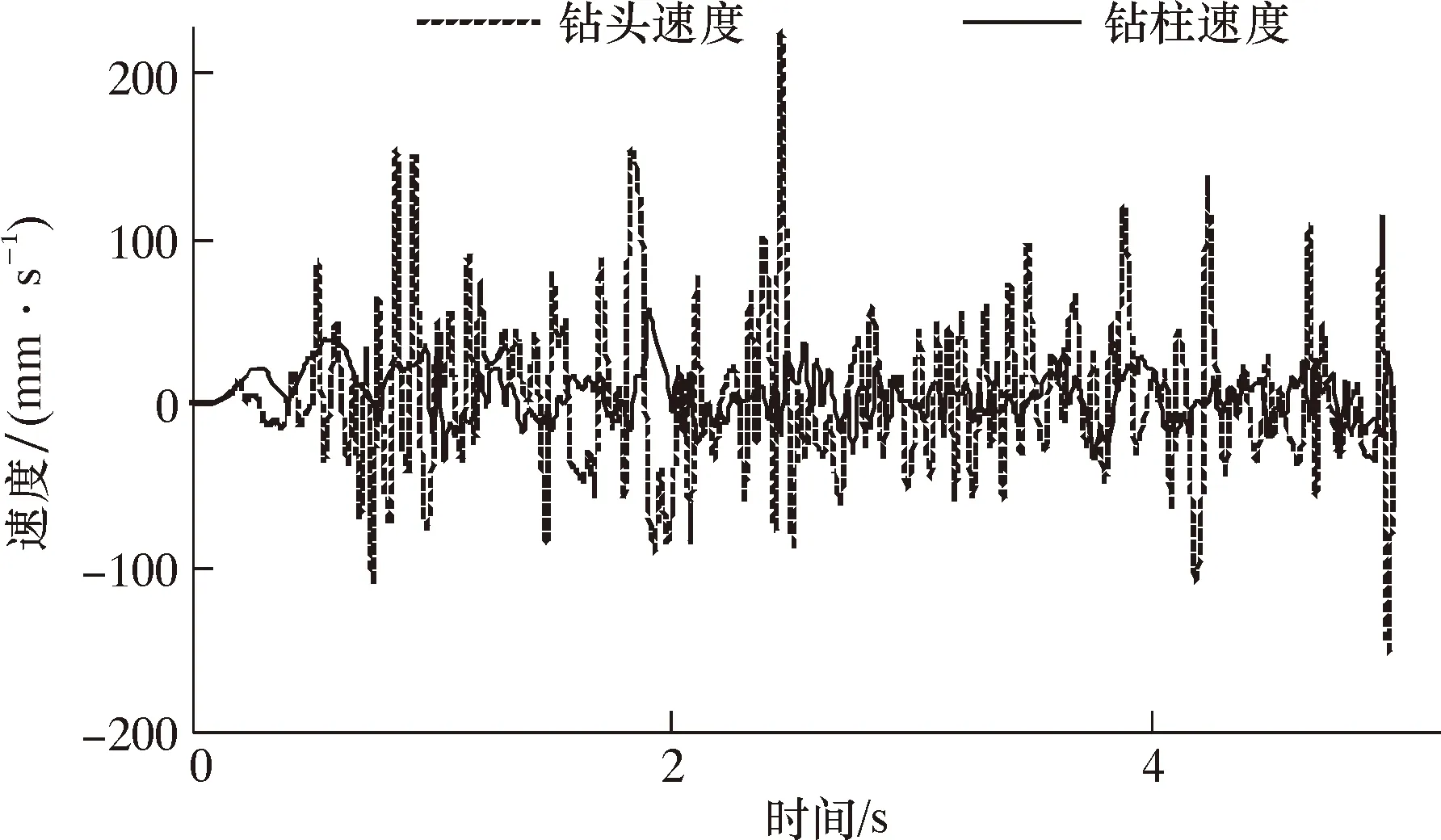
图5 应用减振器后钻头和钻柱速度响应曲线Fig.5 Velocity response curves of bit and drill string after application of shock absorber
在钻井工程中,下部钻具疲劳失效主要是因为动载产生的交变应力,由于下部钻具系统刚度矩阵的改变,确切的说是钻头上方钻具纵向刚度的改变使其运动特性无法全面反映减振器的应用效果,所以在后文的研究中均以纵向力作为分析依据。
3.3 减振器参数对其应用效果的影响
刚度、阻尼和安装位置是影响减振器应用效果的关键参数,在钻具中加入减振器后,系统原有的刚度和阻尼特性发生改变,这也是减振器影响下部钻具动力学特性的根本原因。
3.3.1 减振器刚度对应用效果的影响
保持其他参数不变,减振器刚度k分别为3.5、4.5和6.5 kN/mm时,减振器应用效果如图6~图8所示。从图6~图8可以看出,当减振器刚度为3.5、4.5和6.5 kN/mm时,钻头钻压平均振幅分别3.9、4.0和4.6 kN,钻柱纵向力平均振幅分别为2.6、2.8和3.8 kN。结合图4分析结果,减振器刚度越小,减振器应用效果越好,当减振器刚度从3.5 kN/mm增大至6.5 kN/mm时,钻头平均振幅增大了18%,钻柱平均振幅增大了46%。
3.3.2 减振器阻尼对应用效果的影响
井下系统的阻尼主要包括钻具与井壁的库伦阻尼(摩擦阻尼)、钻井流体的黏性阻尼以及钻具本身的材料阻尼和结构阻尼。在钻具振动过程中,上述阻尼的主要作用在于吸收振动能量,加速钻具振动衰减,这也是目前对阻尼的普遍认识。
同上述阻尼一样,减振器阻尼也同样具有吸收能量和加速振动衰减的作用,且阻尼越大的减振器吸收振动能量的能力越强。在研究减振器阻尼对其减振效果的影响时,仅仅考虑其对振动能量的吸收作用还不够,需要更进一步分析其对减振器上下两端钻具的振动特性影响。
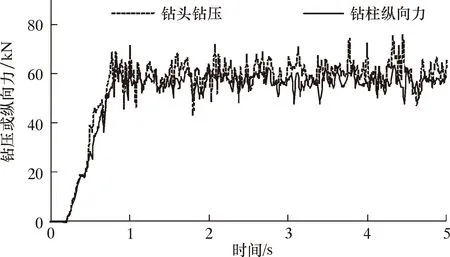
图6 k=3.5 kN/mm时钻头钻压和钻柱纵向力响应曲线Fig.6 Response curves of WOB and drill string longitudinal force at k=3.5 kN/mm

图7 k=4.5 kN/mm时钻头钻压和钻柱纵向力响应曲线Fig.7 Response curves of WOB and drill string longitudinal force at k=4.5 kN/mm

图8 k=6.5 kN/mm时钻头钻压和钻柱纵向力响应曲线Fig.8 Response curves of WOB and drill string longitudinal force at k=6.5 kN/mm
保持其他参数不变,取减振器阻尼c分别为20、40、60和100 N·s/mm时,钻头和钻柱振动情况如图9~图12所示。从图9~图12可以得出,当减振器阻尼分别为20、40、60和100 N·s/mm时,钻头钻压平均振幅分别为6.6、5.1、3.8和4.5 kN,钻柱纵向力平均振幅分别为4.7、3.2、2.5和3.7 kN。结合图4的分析:当减振器阻尼小于60 N·s/mm时,其对钻头和钻柱的减振效果均随其阻尼增大而增大;当减振器阻尼从20 N·s/mm增大至60 N·s/mm时,钻头平均振幅降低了42%,钻柱平均振幅降低了47%;减振器阻尼从60 N·s/mm增大至100 N·s/mm时,钻头平均振幅增加了18%,钻柱平均振幅增加了48%。
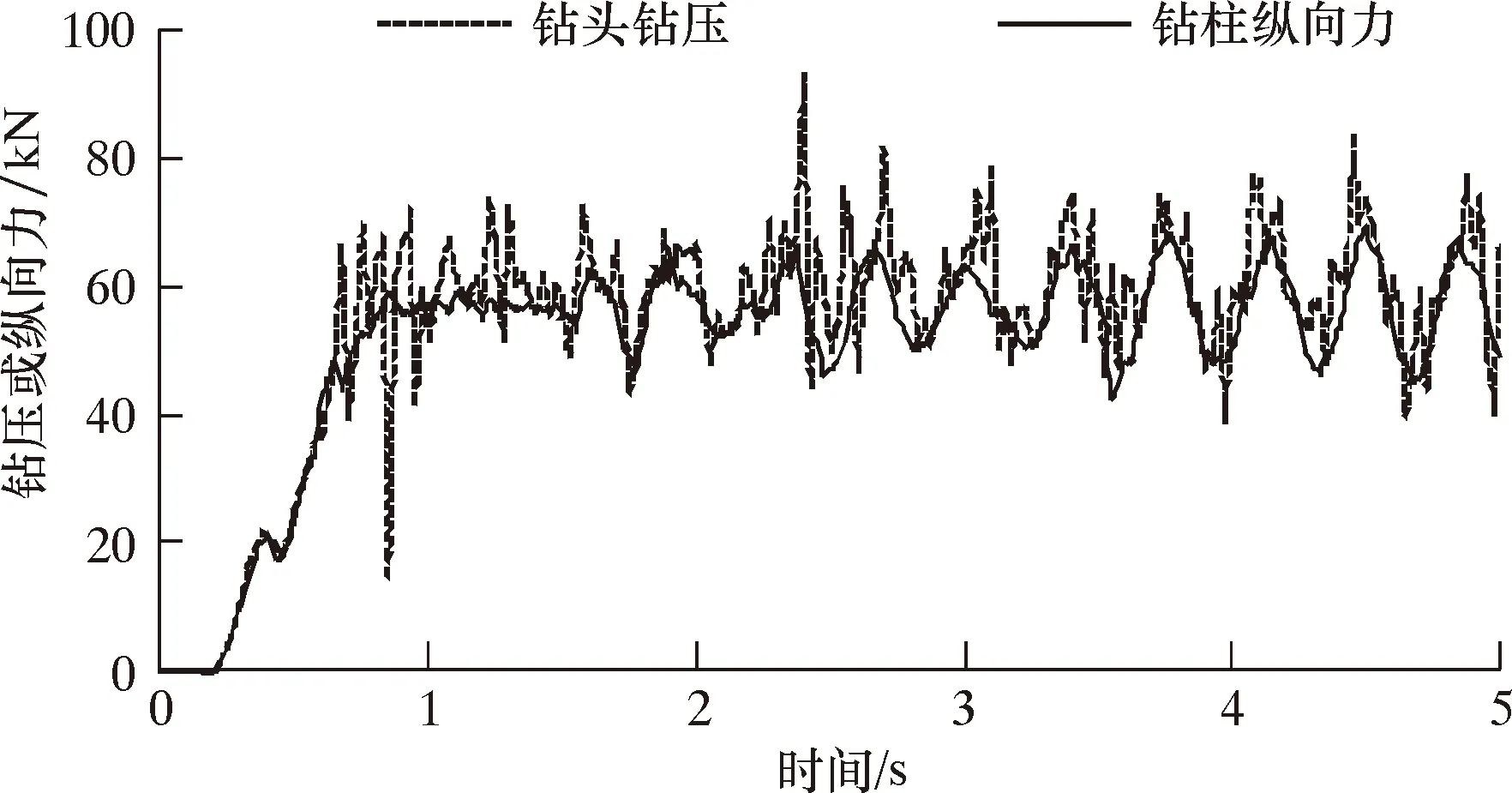
图9 c=20 N·s/mm时钻头钻压和钻柱纵向力响应曲线Fig.9 Response curves of WOB and drill string longitudinal force at c=20 N·s/mm

图10 c=40 N·s/mm时钻头钻压和钻柱纵向力响应曲线Fig.10 Response curves of WOB and drill string longitudinal force at c=40 N·s/mm
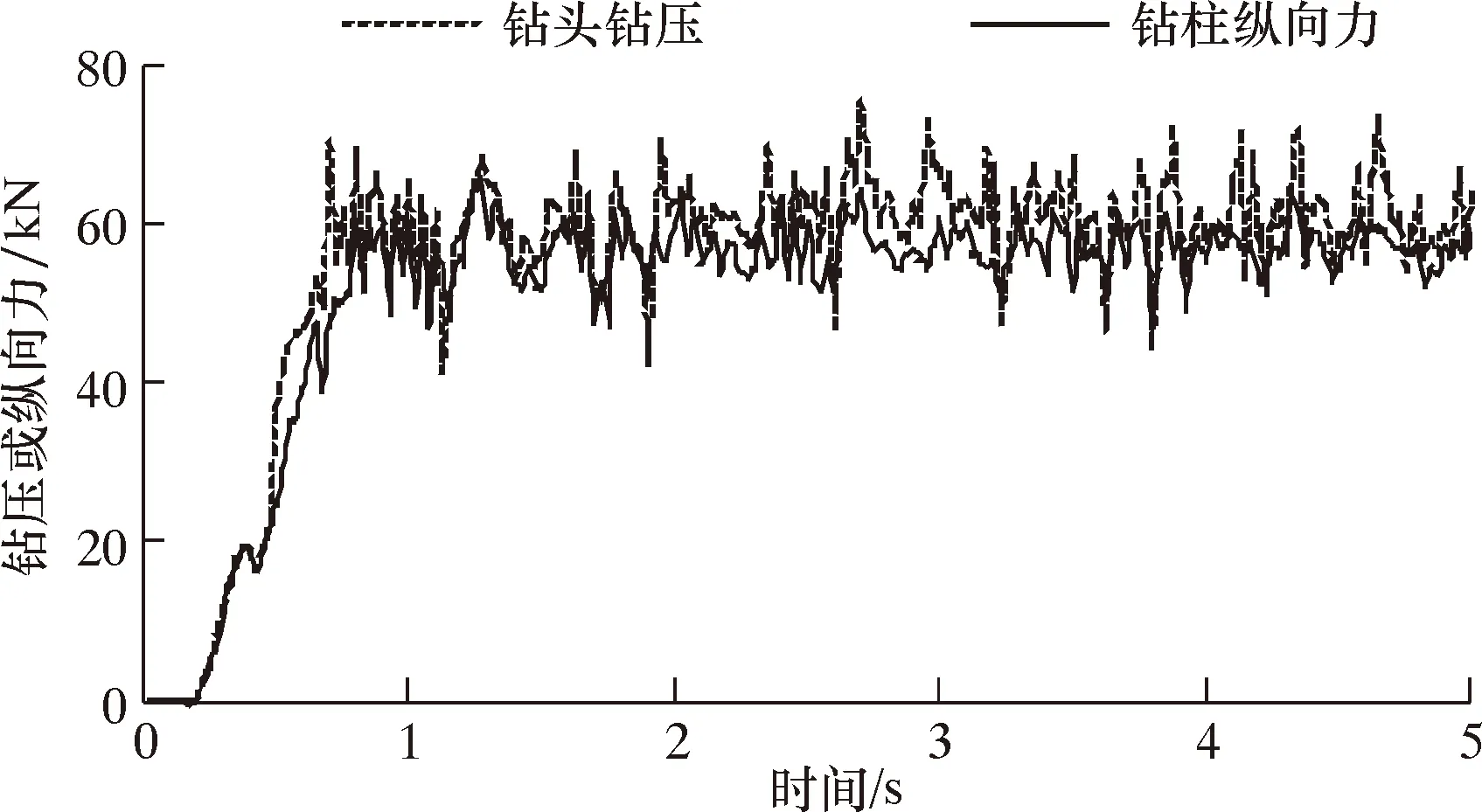
图11 c=60 N·s/mm时钻头钻压和钻柱纵向力响应曲线Fig.11 Response curves of WOB and drill string longitudinal force at c=60 N·s/mm
图12 c=100 N·s/mm时钻头钻压和钻柱纵向力响应曲线Fig.12 Response curves of WOB and drill string longitudinal force at c=100 N·s/mm
从以上分析可以看出,从减振的角度出发,减振器阻尼具有一个最优值,对于本文所选用的钻具组合和钻井参数,减振器阻尼为60 N·s/mm时应用效果最优。
3.3.3 减振器安装位置对应用效果的影响
保持其他参数不变,取减振器与钻头距离s分别为10、19和28 m时,下部钻具纵向振动特性如图13~图15所示。
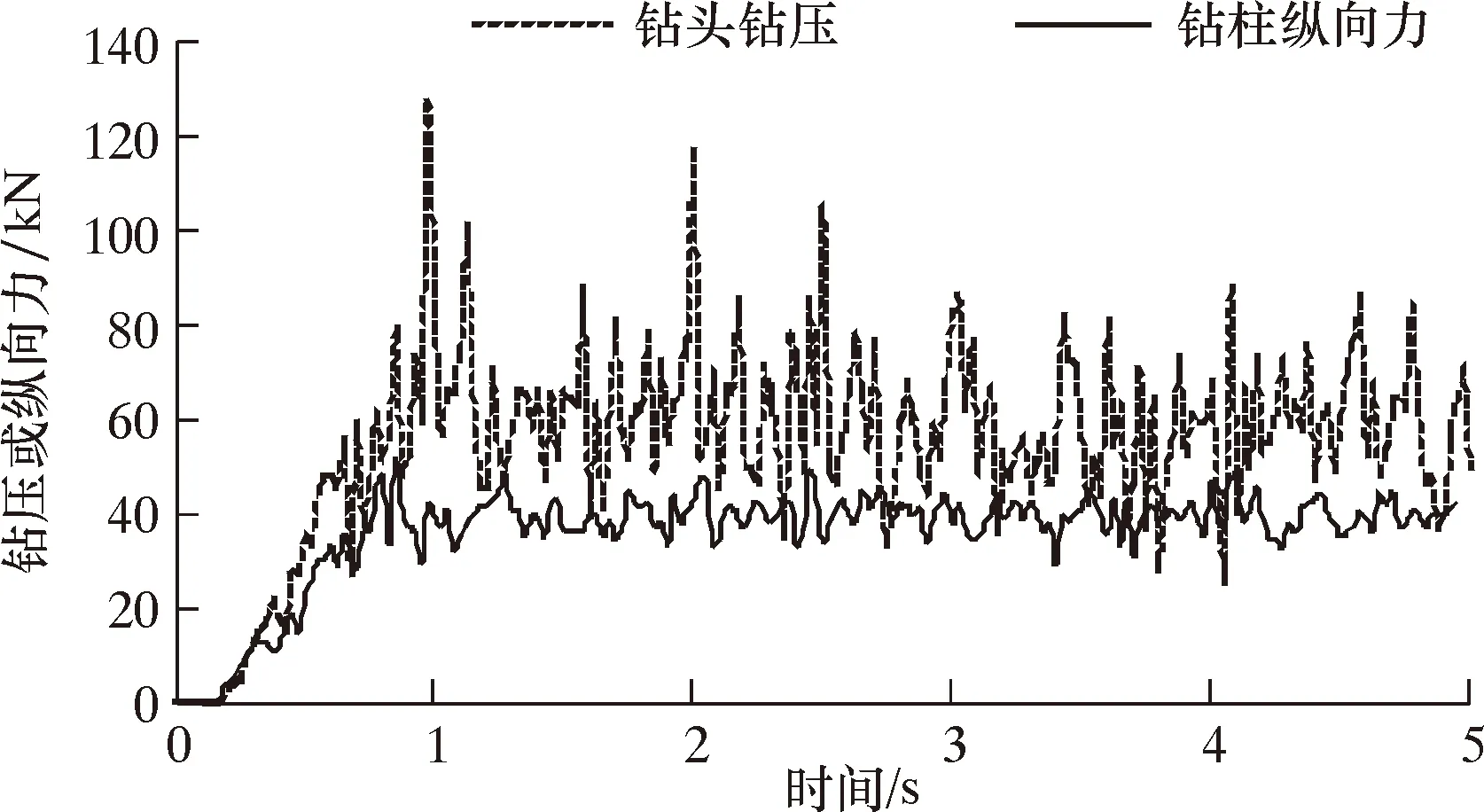
图13 s=10 m时钻头钻压和钻柱纵向力响应曲线Fig.13 Response curves of WOB and drill string longitudinal force at s=10 m
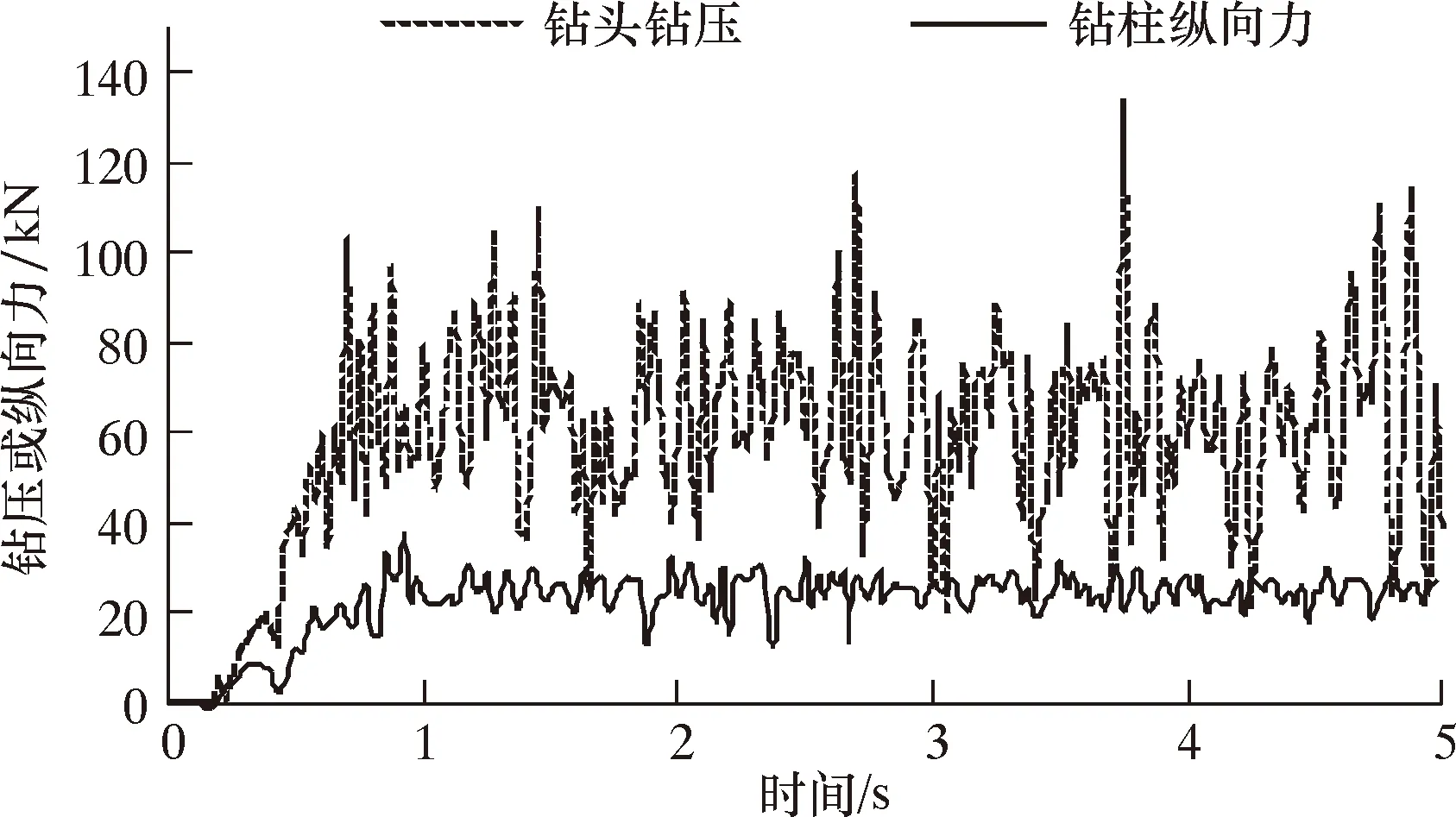
图14 s=19 m时钻头钻压和钻柱纵向力响应曲线Fig.14 Response curves of WOB and drill string longitudinal force at s=19 m
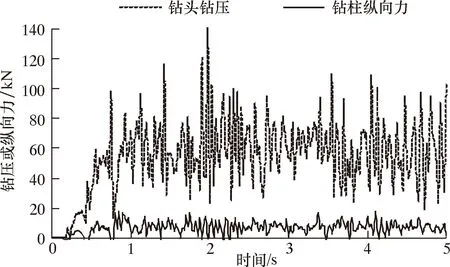
图15 s=28 m时钻头钻压和钻柱纵向力响应曲线Fig.15 Response curves of WOB and drill string longitudinal force at s=28 m
从图13~图15可以得出,减振器距钻头10、19和28 m时,钻头钻压平均振幅分别为11.1、15.8和17.9 kN,钻柱纵向力平均振幅分别为2.8、2.9和3.2 kN。结合前文分析结果可知,随着减振器与钻头距离增大,其对钻头的减振效果大幅度降低,减振器从距钻头1 m移至28 m时,钻头平均振幅增大了337%;减振器安装位置对钻柱振动强度的影响远小于钻头,减振器从距钻头1 m移至28 m时,钻柱平均振幅仅增大3%。
综合以上分析,减振器安装位置对其下端钻头的影响远大于上端钻柱,建议减振器尽可能地靠近钻头安装。
4 结论和建议
(1)在考虑钻柱、钻头和岩石系统动力耦合的基础上,以钻头破岩的动态过程作为井底边界条件,研究了减振器对其上端钻柱和下端钻头的减振效果,并在此基础上对减振器刚度、阻尼和安装位置等参数进行了优选。
(2)减振器对其上端钻柱和下端钻头的受力和运动特性的影响存在差异,应用减振器后,其上端钻柱的纵向力和速度的平均振幅都得到有效降低;下方钻头钻压平均振幅大幅度降低,但其振动速度变化不大。考虑到钻具疲劳失效主要是因为动载产生的交变应力,建议以钻柱和钻头纵向力作为减振器应用效果评价依据。
(3)减振器刚度越小,应用效果越好;减振器阻尼具有一个最优值,对于本文所选用的钻具组合和钻井参数,减振器阻尼为60 N·s/mm时应用效果最优;随着减振器与钻头距离增大,其对钻头的减振效果大幅度降低,而对其上部钻具的影响不大,建议减振器尽可能地靠近钻头安装。
(4)减振器阻尼可以有效降低钻具振动强度峰值,且阻尼最优值受减振器刚度和井下工况影响,建议开展深入研究。

