统计与概率创新题赏析

■甘肃省陇南市礼县职业中等专业学校 杨 虎 王志雄

概率与统计是新课标实施后变化较大的一个内容,有人曾戏称“概率与统计是新课改后逐步登上高考舞台的新生花旦”!经过多年观察,不难发现概率与统计试题一般在新颖、生活化的情境中,考查同学们分析数据、提取信息、解决实际问题的能力。所以,不论是高考数学试题还是竞赛数学试题,命题者越来越注重问题情境的设置,选取一些贴近生活、紧扣热点、反映潮流的新颖素材来包装,以体现概率与统计的应用价值,以期达到解决现实问题之目的。下面选取近两年各类数学考试中统计与概率的新颖试题进行归纳赏析。

一、概率与区域面积牵手

例1 (2 0 1 6年高考全国Ⅱ卷理科)从区间 [0 ,1]随机抽取2n个数x1,x2,…,xn,y1,y2,…,yn,构成n个数对(x1,y1),(x2,y2),…,(xn,yn),其中两数的平方和小于1的数对共有m个,则用随机模拟的方法得到的圆周率π的近似值为( )。

解析：如图1,由题意得:(xi,yi)(i=1,2,…,n)在如图1所示的方格中,而平方和小于1的点均在图中所示的阴影中,由几何概率知识可得,圆形的面积和正方形的面故选C。

图1

点评:求解与面积有关的几何概型问题,关键是弄清某事件对应的面积,必要时可根据题意构造两个变量,把变量看成点的坐标,找到全部试验结果构成的平面图形,以便求解。

例2 如图2,设抛物线y=-x2+1的顶点为A,与x轴正半轴的交点为B,设抛物线与两坐标轴正半轴围成的区域为M,随机往M内投一点P,则点P落在△A O B内的概率是( )。

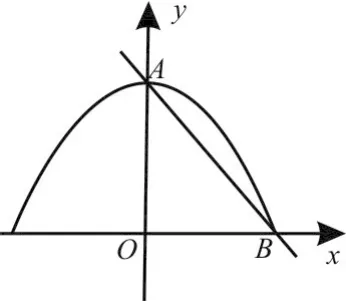
图2

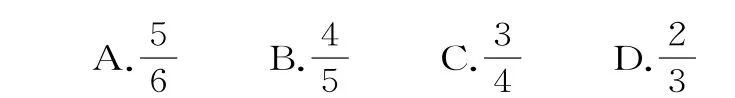
解析：设抛物线y=-x2+1与x轴正半轴及y轴的正半轴所围成的区域的面积为。设事件N=“随机往M内投一点P,则点P落在△A O B内”,则:

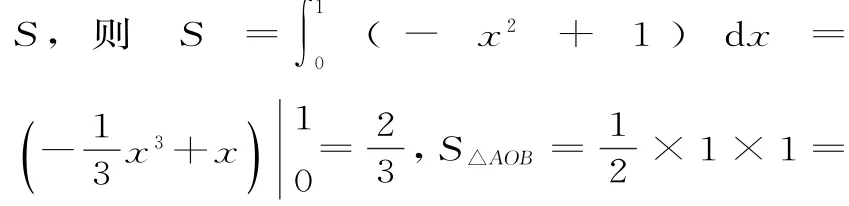
点评:以函数为命题背景考查概率知识是本题的一大亮点,可以体会到近几年在对概率的考查上重视命题背景,突出概率与其他知识的交汇,应引起同学们的重视。

二、概率与情景问题交融

例3 (2 0 1 6年高考全国Ⅰ卷理科)某公司的班车在7:0 0,8:0 0,8:3 0发车,小明在7:5 0至8:3 0之间到达发车站乘坐班车,且到达发车站的时刻是随机的,则他等车时间不超过1 0分钟的概率是( )。

解析：由题意画出时间轴如图3所示,小明到达的时间会随机的落在图中线段A B中,而当他到达的时间落在线段A C或D B时,才能保证他等车的时间不超过1 0分钟。于是,根据几何概型,小明等车时间不超过1 0分钟的概率为,故选B。

图3

点评:求解几何概率问题的关键是确定“测度”,常见的测度有:长度、面积、体积等。本题将几何概率与班车发车的时间段联系起来,即命题以时间段为“测度”,打破以往常规几何模式思维,整道题目显得新颖别致,同时又体现了数学来源于实际生活,又服务于实际生活的理念。

三、概率与体育竞赛同行

例4 甲、乙两名跳高运动员一次试跳2米高度成功的概率分别是0.7,0.6,且每次试跳成功与否相互之间没有影响,求:

(1)甲试跳三次,第三次才成功的概率;

(2)甲、乙两人在第一次试跳中至少有一人成功的概率;

(3)甲、乙各试跳两次,甲比乙的成功次数恰好多一次的概率。

解析：记“甲第i次试跳成功”为事件,“乙第i次试跳成功”为事件Bi,依题意

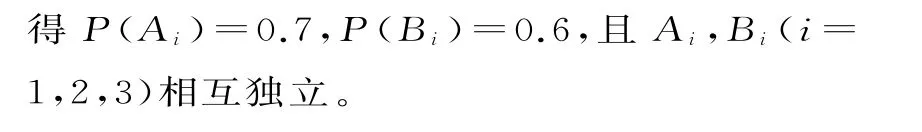
(1)“甲第三次试跳才成功”为事件,且三次试跳相互独立,所以

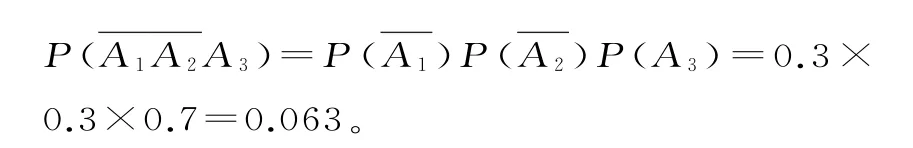
(2)“甲、乙两人在第一次试跳中至少有一人成功”为事件C。

方法1:因为且彼此互斥,所以:

方法21-0.3×0.4=0.8 8。

(3)设“甲在两次试跳中成功i次”为事件Mi(i=0,1,2),“乙在两次试跳中成功i次”为事件)。因为事件“甲、乙各试跳两次,甲比乙的成功次数恰好多一次”可表示为,且为互斥事件,所以所求的概率为:

点评:本题主要考查体育竞赛中互斥事件下的概率的计算,分析时一定要紧扣定义“事件A与事件B不可能同时发生是指若事件A发生,事件B就不发生或者事件B发生,事件A就不发生”来判断是否互斥。概率在体育竞赛中有重要的应用,学习时应当重视这个命题背景。

例5 某校在一次趣味运动会的颁奖仪式上,高一、高二、高三各代表队人数分别为1 2 0人、1 2 0人、n人。为了活跃气氛,大会组委会在颁奖过程中穿插抽奖活动,并用分层抽样的方法从三个代表队中共抽取2 0人在前排就座,其中高二代表队有6人。

(1)求n的值。

(2)把在前排就座的高二代表队6人分别记为a,b,c,d,e,f,现随机从中抽取2人上台抽奖,求a和b至少有1人上台抽奖的概率。

(3)抽奖活动的规则是:代表通过操作按键使电脑自动产生两个[0,1]之间的均匀随机数x,y,并按如图4所示的程序框图执行。若电脑显示“中奖”,则该代表中奖;若电脑显示“谢谢”,则不中奖,求该代表中奖的概率。

图4

解析：(1)根据分层抽样可得 6=1 2 0

(2)高二代表队6人,从中抽取2人上台抽奖的基本事件有(a,b),(a,c),(a,d),(a,e),(a,f),(b,c),(b,d),(b,e),(b,f),(c,d),(c,e),(c,f),(d,e),(d,f),(e,f)共1 5种,其中a和b至少有1人上台抽奖的基本事件有9种,所以a和b至少有1人上台抽

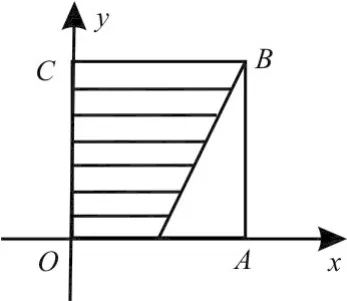
图5

奖的概率为区域为如图5中的阴影部分。

直线方程2x-y-1=0,令y=0,可得于是在x,y∈

[0,1]时满足2x-y-1≤0的区域的面积为

所以该代表中奖的概率为

点评:本题将当今社会热门活动——抽奖与概率知识结合,让试题增加了趣味性,而抽奖活动生活中比比皆是,以抽奖为背景命题给同学们一个熟悉的生活情境,体现了数学知识与生活的密切联系。

四、概率与新概念结合

例6(2 0 1 5年高考福建卷文科)全网传播的融合指数是衡量电视媒体在中国网民中影响力的综合指标。根据相关报道提供的全网传播2 0 1 5年某全国性大型活动的“省级卫视新闻台”融合指数的数据,对名列前2 0名的“省级卫视新闻台”的融合指数进行分组统计,结果如表1所示。

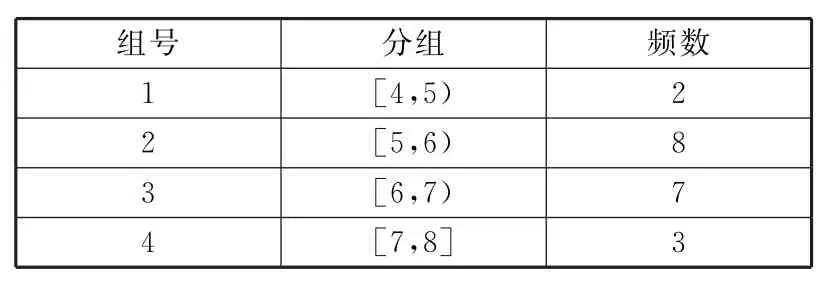
表1

(1)现从融合指数在[4,5)和[7,8]内的“省级卫视新闻台”中随机抽取2家进行调研,求至少有1家的融合指数在[7,8]的概率;

(2)根据分组统计表求这2 0家“省级卫视新闻台”的融合指数的平均数。

解析：(1)融合指数在[7,8]内的“省级卫视新闻台”记为A1,A2,A3;融合指数在[4,5)内的“省级卫视新闻台”记为B1,B2。从融合指数在[4,5)和[7,8]内的“省级卫视新闻台”中随机抽取2家的所有基本事件是:{A1,A2},{A1,A3},{A2,A3},{A1,B1},{A1,B2},{A2,B1},{A2,B2},{A3,B1},{A3,B2},{B1,B2},共1 0个。

其中,至少有1家融合指数在[7,8)内的基本事件是:{A1,A2},{A1,A3},{A2,A3},{A1,B1},{A1,B2},{A2,B1},{A2,B2},{A3,B2},{A3,B2},共9个。所以所求的概率

(2)这2 0家“省级卫视新闻台”的融合指数平均数等于

点评:融合指数是新闻专业里的“术语”,在本题中题目做了说明:全网传播的融合指数是衡量电视媒体在中国网民中影响力的综合指标。越来越注重数学与生活的联系是高考命题的趋势之一,本题的命题背景体现了关注生活也就是关注数学的理念。

例7某次测量发现一组数据(xi,yi)具有较强的相关性,并计算得^y=x+1,其中数据(1,y0),y0因书写不清,只记得y0是[0,3]内的任意一个值,则该数据对应的残差的绝对值不大于1的概率为 。(残差=真实值-预测值)

解析：由^y=x+1,得^y0=1+1=2,于是预测值为2。由于|y0-2|≤1,因此1≤y0≤3。当y0∈[1,3]时,数据对应的残差的绝对值不大于1,由于y0是[0,3]内的任意一个值,因此数据对应的残差的绝对值不大于1的概率

点评:根据“残差=真实值-预测值”来进行计算是本题的突破口。新概念题目比较注重对同学们阅读理解能力的考查,所以平时对阅读理解型题目的学习与积累是非常有必要的。

五、概率与二进制交融

例8 (2 0 1 6年安徽省高中数学竞赛)等可能地随机产生一个正整数x∈{1,2,…,20 1 6},则x在二进制下的各位数字之和不超过8的概率等于 。{0,1}。我们考查满足的x的个数,其充分必要条件为p≥9-p,因此x的个数为

=5 1。从q而x在二进制下的各位数字之和不超过8的个数为20 1 6-5 1=19 6 5,因此所求概率为

点评:二进制是计算机技术中广泛采用的一种数制,本题将二进制与概率融合,考查方式新颖而独特,体现了竞赛题的高立意,新视角。

六、概率与各色小球共舞

例9 (2 0 1 6年高考北京卷理科)袋中装有偶数个球,其中红球、黑球各占一半。甲、乙、丙是三个空盒,每次从袋中任意取出两个球,将其中一个球放入甲盒,如果这个球是红球,就将另一个球放入乙盒,否则就放入丙盒。重复上述过程,直到袋中所有球都被放入盒中,则( )。

A.乙盒中黑球不多于丙盒中黑球B.乙盒中红球与丙盒中黑球一样多C.乙盒中红球不多于丙盒中红球

D.乙盒中黑球与丙盒中红球一样多

解析：若乙盒中放入的是红球,则须保证抽到的两个均是红球;若乙盒中放入的是黑球,则须保证抽到的两个球是一红一黑,且红球放入甲盒;若丙盒中放入的是红球,则须保证抽到的两个球是一红一黑,且黑球放入甲盒;若丙盒中放入的是黑球,则须保证抽到的两个球都是黑球;由于抽到的两个球是红球和黑球的次数是奇数还是偶数无法确定,故无法判定乙盒和丙盒中异色球的大小关系,而抽到两个红球的次数与抽到两个黑球的次数应是相等的,故选C。

点评:本题将小球与概率知识结合,创新味十足,命题立意在出现情况的等可能性。如果所求事件对应的基本事件有多种可能,那么一般我们通过逐一列举计数,再求概率,此题即是如此。列举的关键是要有序(有规律),从而确保不重不漏。

七、概率与直线和圆交汇

例1 0 (2 0 1 6年高考山东卷理科)在[-1,1]上随机地取一个数k,则事件“直线y=k x与圆(x-5)2+y2=9相交”发生的概率为 。

解析：直线y=k x与圆(x-5)2+y2=9相交,需要满足圆心到直线的距离小于半径,是所求概率

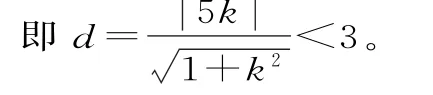
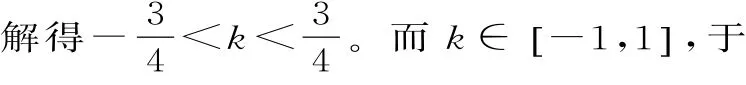
点评:本题综合性较强,具有“无图考图”的显著特点,几何概型概率的计算问题,当涉及圆心距的计算与弦长相关的问题时往往要关注“圆的特征直角三角形”。在直线与圆的知识和概率知识的交汇处命题,较好地考查了同学们分析问题解决问题的能力以及运算能力。

八、概率与平面向量相伴

例1 1 (2 0 1 6

年高考上海卷理科)如图6,在平面直角坐标系x O y中,O为正八边形A1A2…A8的中心,A1(1 ,0)。任取不同的两点Ai,Aj,点P满=0,则点P落在第一象限的概率是 。

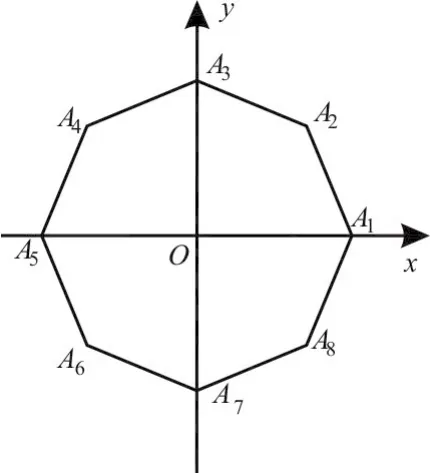
图6

解析：根据题意分析知共有C28=2 8(种)基本事件,其中使点P落在第一象限共有(种)基本事件,故所求概率为

点评:本题是概率新考题型,在概率的计算上做文章,考查同学们思维的灵活性。解答本题的关键是从坐标系中的平面向量知识入手,准确确定所研究对象的基本事件空间、基本事件个数,利用概率的计算公式求解。对增强同学们数学应用意识、基本运算求解能力不无裨益。

九、概率与实际应用牵手

例1 2 (2 0 1 5年高考北京卷文科)某超市随机选取10 0 0位顾客,记录了他们购买甲、乙、丙、丁四种商品的情况,整理成如下统计表,如表2,其中“√”表示购买,“×”表示未购买。

表2

(1)估计顾客同时购买乙和丙的概率;

(2)估计顾客在甲、乙、丙、丁中同时购买3中商品的概率;

(3)如果顾客购买了甲,则该顾客同时购买乙、丙、丁中哪种商品的可能性最大?

解析：(1)从统计表可以看出,在这10 0 0位顾客中,有2 0 0位顾客同时购买了乙和丙,所以顾客同时购买乙和丙的概率可以估计为

(2)从统计表可以看出,在这10 0 0位顾客中,有1 0 0位顾客同时购买了甲、丙、丁,另有2 0 0位顾客同时购买了甲、乙、丙,其他顾客最多购买了2种商品。所以顾客在甲、乙、丙、丁中同时购买3种商品的概率可以估计

(3)与(1)同理,可得:

顾客同时购买甲和乙的概率可以估计为

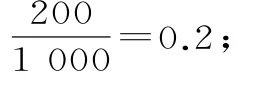
顾客同时购买甲和丙的概率可以估计为

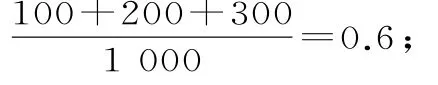
顾客同时购买甲和丁的概率可以估计为

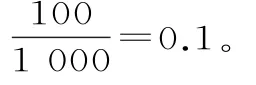
所以,如果顾客购买了甲,则该顾客同时购买丙的可能性最大。

点评:本题主要考查统计表、概率等基础知识,考查同学们的分析问题解决问题的能力、转化能力、计算能力。第一问,由统计表读出顾客同时购买乙和丙的人数2 0 0,计算出概率;第二问,先由统计表读出顾客在甲、乙、丙、丁中同时购买3种商品的人数1 0 0+2 0 0,再计算概率;第三问,由统计表读出顾客同时购买甲和乙的人数为2 0 0,顾客同时购买甲和丙的人数为1 0 0+2 0 0+3 0 0,顾客同时购买甲和丁的人数为1 0 0,分别计算出概率,再通过比较大小得出结论。