布谷鸟优化的密度峰值快速搜索聚类算法

郑 虹， 周丽媛， 韩旭明

(长春工业大学 计算机科学与工程学院， 吉林 长春 130012)

0 引 言

聚类是数据挖掘领域的一个重要分支，在无监督条件下用于挖掘数据潜在结构。目前已经成功应用于计算机科学、地理科学和经济领域[1-2]。聚类是根据数据样本之间的相似性，将空间中n个数据样本划分成合理类簇的过程,聚类结果使得同一类簇内的样本具有较高相似性,不同类簇间的样本具有较低相似性[3-5]。没有任何一种聚类算法能够适用于不同数据集所呈现的结构[6]。鉴于此，针对不同数据集,多种不同聚类方法提出,传统的聚类分析算法有分式聚类方法、层次聚类方法、基于密度的聚类方法和基于网格的聚类方法。

DPC算法是一种基于密度的聚类算法，由Alex Rodriguez等[7]在Science杂志上提出。DPC算法基于局部数据点的密度进行聚类，能够聚成任意形状的类簇。其局部密度点计算方法灵感来源于均值偏移理论[8]；其聚类分配与K中心聚类算法[9]相似，确定中心点后，将剩余数据点根据其与中心点的相似度分配给最近的中心点。K中心算法需要反复迭代确定聚类中心，具有较高复杂度。DPC算法不需要反复迭代确定聚类中心，而是通过密度大小和距离远近，人为手动划出聚类中心，降低多次寻找聚类中心的复杂度。Alex Rodriguez认为潜在聚类中心为：数据点自身要有较高密度，且距离其他密度更高点的距离较远。

布谷鸟算法是由Xin-She Yang和Suash Deb两位学者于2009年提出，该算法利用布谷鸟特殊的繁育寄生机理和Levy飞行搜索机制，模拟出布谷鸟寻窝产卵行为的一种群体智能优化算法。CS算法凭借Levy飞行随机游动和偏好游动策略，在求解优化问题时具有较好性能。其具有参数少、逻辑结构简单、全局搜索能力强等优点,目前已经成功用于求解多种工程优化问题，如异构系统任务分配问题、无线传感器网络定位问题。

针对不同类型数据，DPC算法具有较好聚类结果，但其也存在一些缺陷。

1)文献[7]并没有给出计算截断距离的方法，而聚类结果对于截断距离很敏感。

2)运用欧氏距离作为聚类相似度的度量标准，该标准忽略了数据间的方向信息。众多学者对其进行研究与改进[10-20]。针对上述DPC算法的缺陷，提出布谷鸟优化的密度峰值快速搜索聚类算法。首先运用布谷鸟算法[21]优化截断距离，根据布谷鸟搜索算法较强全局搜索能力，可以寻找到最优的截断距离值。其次引入余弦相似度，基于方向与距离相结合的相似度能更好区分一些距离相等方向不同点的数据点，特别是对于两个类簇中间区域点的划分。对于两个类簇的中间区域数据点，其到两个聚类中心距离一样，算法在对该点进行分配时，可能会随机分配，每次实验会分配给不同的聚类中心，出现误差，引入余弦相似度后，会避免这种情况发生。实验结果表明，布谷鸟优化的密度峰值快速搜索聚类算法与DPC算法相比，具有较好的聚类效果。

1 相关工作

1.1 DPC 算法

DPC算法的基本原理是以空间中任意两点间欧氏距离为基础，假定聚类中心的局部密度大于其附近邻居点局部密度，并且与密度更大数据点间距离(非欧氏距离)较远。为找到满足以上两个特点的聚类中心，DPC算法引入两个量：

1)数据点i的局部密度ρi；

2)到比数据点i的局部密度大的数据点集合中，距离其最近点的距离δi。

文献[7]认为，当数据点集合较大时，计算数据点i的局部密度:

ρi=∑χ(dij-dc)

(1)

其中：

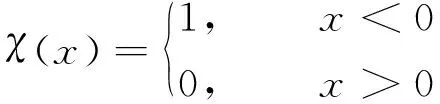
当数据点集合较小时，用指数核[7]计算数据点的局部密度ρi,计算公式为：

(2)

其中,dij为数据点i和j间的欧氏距离,dc>0,为截断距离,需手动给出。

计算数据点i的距离公式为：

(3)

对于局部密度最大数据点i的距离公式为：

(4)

文献[7]采用决策图的方式，认为ρi和δi都比较大的点有可能成为聚类中心。

DPC算法步骤如下:

1)初始化截断距离dc，计算任意两点间欧式距离dij，计算每个数据点的密度值ρi,并将其顺序排序，计算判定距离δi；

2)确定聚类中心，并初始化数据点归类属性标记；

3)对非聚类中心数据点进行归类；

4)将每个簇类中的数据点划分为核心点和边缘点。

1.2 布谷鸟算法

布谷鸟算法是一种优化算法，由Xin-She Yang等[21]提出。基于布谷鸟产卵习性和3条理想规则提出布谷鸟搜索算法。3条理想规则为：

1)每次只产1个蛋，并随机选择鸟巢孵化;

2)在随机选择的一组鸟巢中，最好的鸟巢位置被保留到下一代;

3)外来鸟蛋被鸟巢主人发现的概率是Рα∈[0,1]。

布谷鸟寻找下一代鸟窝位置χ(t+1)的更新公式为：

⊕Levy(λ)

(5)

式中:t----当前迭代次数；

α----步长控制因子，一般取α=1；

⨁----点对点乘法；

Levy(λ)----随机搜索路径，服从Levy分布，满足Levy～u=t-λ(1<λ≤3)。

鸟窝位置更新后，产生随机数k∈(0,1)与被发现概率Рα对比，大于被发现概率,则对当前鸟巢位置更新，否则不变。

布谷鸟算法的实现步骤：

1)初始化种群，随机产生n个鸟巢初始位置，并设置相关参数；

2)计算每个鸟巢的适应度值，并保留当前最优解；

3)每个鸟巢位置按照式(5)进行更新；

4)计算目标函数适应度值，如果优于上一代适应度值，则鸟巢位置保留到下一代，否则保持原来鸟巢位置不变；

5)产生随机数k，如果k大于被发现概率Рα，改变鸟巢位置，否则保持原来位置不变。

6)判断当前最优解是否满足条件，满足则输出全局最优解，算法结束，否则转2)。

1.3 余弦相似度

余弦相似度是计算空间数据点间相似度的一种方法。该方法首先将数据点维度映射成空间向量，然后通过计算两个数据点空间向量的夹角余弦值来衡量他们之间的相似性。两个数据点向量夹角越小，即夹角余弦值越大，表明二者的方向越一致，相似度越高；而两个数据点向量夹角越大，即夹角余弦值越小，表明二者的方向越不一致，相似度越低。该值越大，表明夹角越小，即二者的方向越一致，两个向量越相似。两个向量间的余弦值采用欧几里德点积公式计算：

a·b=|a|×|b|cosθ,θ∈[0,2π]

(6)

余弦相似度定义如下：

(7)

式中:xi,xj----空间中任意两点。

1.4 改进的余弦相似度

任意两个向量夹角的余弦相似度是一条余弦曲线，在0°到180°随着角度增加余弦值降低，而180°到360°随着角度增加余弦值增加。鉴于余弦值不能随着角度的增加而增加或者减小，余弦曲线不是单调函数，根据两个数据点间余弦值很难直观地判断数据点间方向，将余弦值取绝对值，引入指数函数，使余弦值随着方向的增加而增加。改进的余弦相似度(方向因子)为：

(8)

2 布谷鸟优化的密度峰值快速搜索聚类算法

鉴于DPC算法截断距离dc需要手动随机给出,利用欧氏距离计算数据点的局部密度，此密度仅考虑到数据点间的距离，而忽略了数据点间的方向信息。对于数据量较大、数据点较为分散的数据结构，数据点间的方向会影响DPC算法聚类效果。提出用布谷鸟算法优化dc，避免手动给出dc,通过引入余弦相似度来增加数据点局部密度的可靠性。

2.1 CS-DPC算法的距离矩阵

对于空间中m个n维数据点χ1,χ2,χ3, …，χm

χ1=(χ11,χ12,χ13,…,χ1n)

χ2=(χ21,χ22,χ23,…,χ2n)

⋮

χm=(χm1,χm2,χm3,…,χmn)

任意两点χi，χj间欧式距离为:

(9)

m个数据点的欧氏距离矩阵为:

欧式距离衡量的是空间中各点的绝对距离，跟各个点所在的位置坐标直接相关。其只考虑数据点间的实际距离，若数据点p到比其大的两个潜在聚类中心距离相等，此时DPC算法的划分准则无法正确分配p。鉴于此，引入余弦相似度的指数形式，保证在欧式距离无法解决数据点分配问题时，提供一个相对较好的解决方案。在每个数据点计算欧式距离基础上引入方向因子,此时,m个数据点的距离矩阵为

(10)

2.2 布谷鸟优化截断距离dc

在DPC算法中，每次执行需要手动输入截断距离dc，原作者并没有给出具体计算dc的规则，导致dc的选取缺少规范性。并且数据集聚类效果对于dc的取值比较敏感，dc取值过大，导致聚类个数多于真实簇类数，相反，dc取值过小，导致聚类个数少于真实簇类数。因此，dc取值大小对DPC算法产生很重要的影响。布谷鸟算法是一种比较新颖的群体智能算法，具有参数少、结构简单等特点。该算法即能通过Levy飞行进行全局搜索，又能通过偏好游动进行局部寻优。鉴于布谷鸟算法的较强全局搜索能力和局部搜索能力，能够发现测试数据集的最优聚类结构，提出引用布谷鸟搜索算法优化dc，Silhouette指标作为目标函数。通过多次迭代，根据最优聚类结果(Silhouette指标最优)输出最优dc值。

布谷鸟优化的密度峰值快速搜索聚类算法步骤如下:

1)初始化种群，种群个数为10(10个鸟巢)，dc取值范围为(Dmin,Dmax)；

2)执行DPC算法，获得Silhouette指标；

3)保留当前最优Silhouette指标；

4)每个dc按照式(6)进行更新；

5)计算每个dc所对应的Silhouette指标，如果优于上一代Silhouette指标，则dc值保留到下一代，否则保持原来dc值不变；

6)产生随机数k，如果k大于被发现概率P，改变dc值，否则保持原来dc值不变；

7)当前最优解不变或者满足最大迭代次数，输出相应的Silhouette指标和截断距离dc，算法结束，否则转2)。

3 实验仿真与分析

3.1 实验数据

为了测试CS-DPC算法的准确性能达到原始DPC 算法的聚类结果，选择5个人工数据集和3个标准UCI数据集进行测试，实验数据见表1。

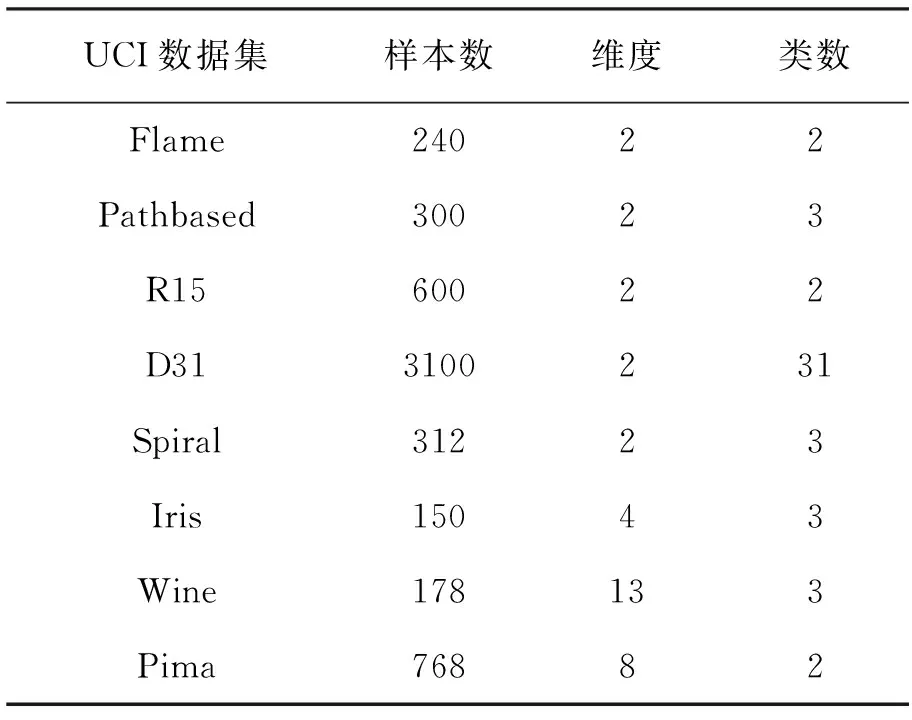
表1 实验数据集

Flame、 Pathbased、 R15 和Spiral是二维并且样本数较少的数据集，D31是二维但数据量相对较大数据集，Iris、 Wine和 Pima是多维数据集。布谷鸟种群规模为 20，迭代次数T=50，Pα=0.25。

3.2 评价指标

为验证CS-DPC算法聚类结果的有效性，引入两个有效性指标来评价DPC算法和CS-DPC算法聚类结果，分别为内部评价指标Silhouette和外部评价指标F-measure。

3.2.1 Silhouette指标

Silhouette指标用来评价聚类效果的内部评价指标。一般定义为，设一个具有n个样本点的数据集被划分为k个聚类Ci(i=1,2,…,k)，a(t)为聚类C中的样本点t与其所在的类中所有其它样本的平均不相似度或距离，d(t,Ci)为Cj的样本t到另一个类Ci的所有样本的平均不相似度或距离，则b(t)=min{d(t,Ci)}，其中i=1,2,…,k,且i≠j。样本t的Silhouette指标:

(11)

聚类中的所有样本的平均Silhouette值表示此类的紧密性和可分性；Silhouette取值范围为[-1,1]，Silhouette指标越大，即越接近1，表示聚类质量越好。

3.2.2 F-measure指标

F-measure指标结合查全率和准确率用来评价聚类效果的外部评价指标。对于一个真实类簇Pj和Ci，其准确率P(i,j)和召回率R(i,j)的定义为:

(12)

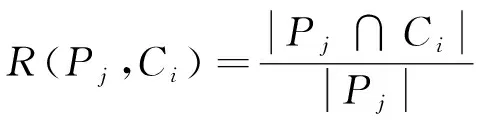
(13)

相应的F-measure指标为：

(14)

将所有类簇的F-measure值加权求平均，得到整个聚类结果的F-measure值。

(15)

其中,N为样本点个数;F-measure值越大，算法越准确。

3.3 实验结果和分析

使用MATLAB对CS-DPC算法和DPC算法进行实验仿真。通过对5个人工数据集和3个标准UCI数据集进行实验仿真，结果表明，CS-DPC算法在聚类效果方面优于DPC算法。

CS-DPC算法和DPC算法聚类结果的评价指标见表2，聚类数目对比见表3。

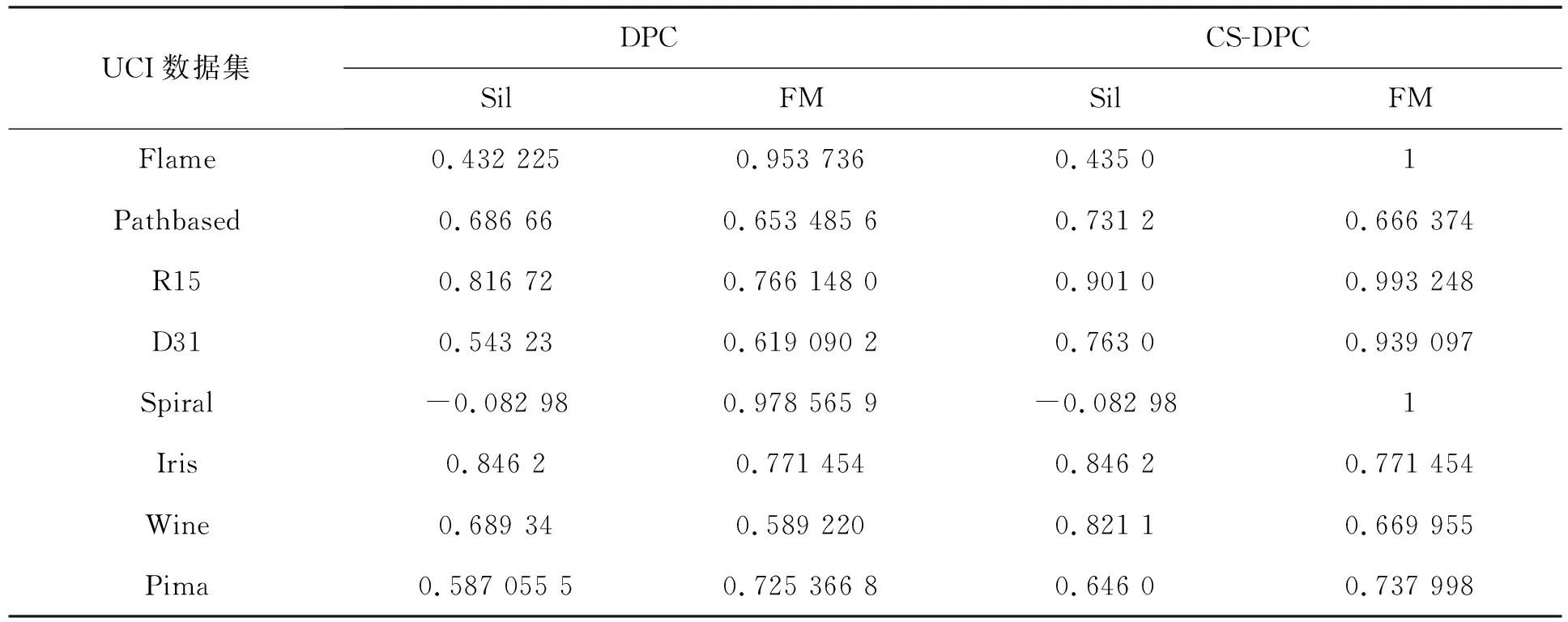
表2 聚类结果的评价指标对比

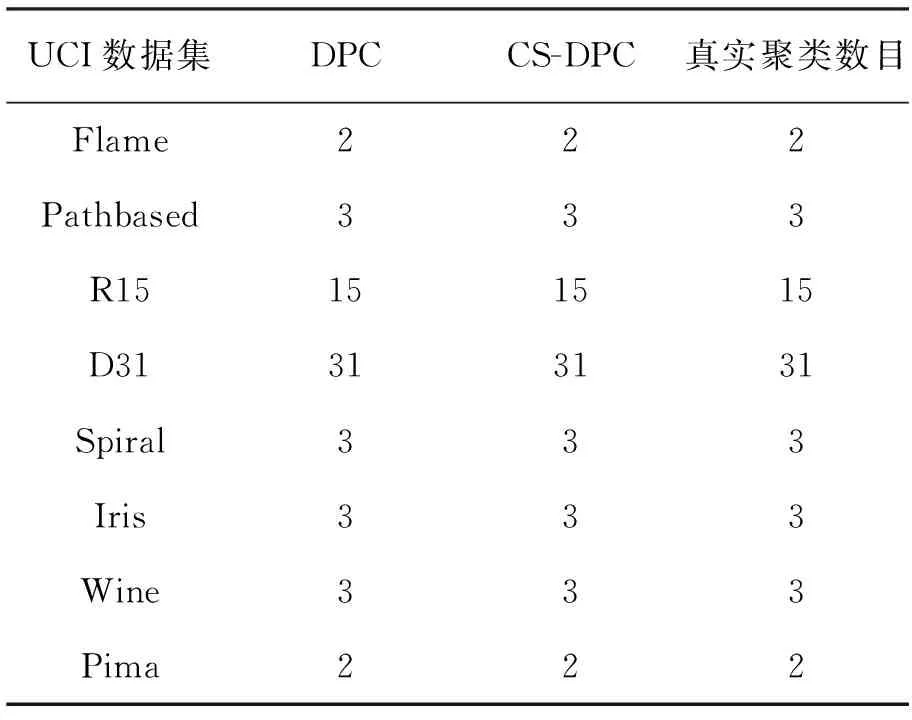
表3 聚类数目对比

从表2可以看出，对于数据集Flame、Pathbased、R15、D31，Wine 和Pima，CS-DPC算法的内部指标Sil 比DPC算法均有所提高，特别是数据集R15和 Pima，CS-DPC算法的Sil比DPC算法提高10%；数据集Wine,CS-DPC算法的Sil比DPC算法提高19%；数据集D31，CS-DPC算法的Sil比DPC算法提高40%。对于数据集Wine、R15和 D31，CS-DPC算法的准确度FM比DPC算法提高13%、29%和51%，特别是对于数据集Flame和Spiral，CS-DPC算法的准确度达到了100%。

从表3可以看出，DPC算法和CS-DPC算法聚类个数均可达到实际聚类个数，DPC算法需手动给出参数dc值，而CS-DPC算法不用给出具体dc值，在一定范围内，通过Levy飞行的全局搜索能力，可以直接给出最优dc值的聚类结果。

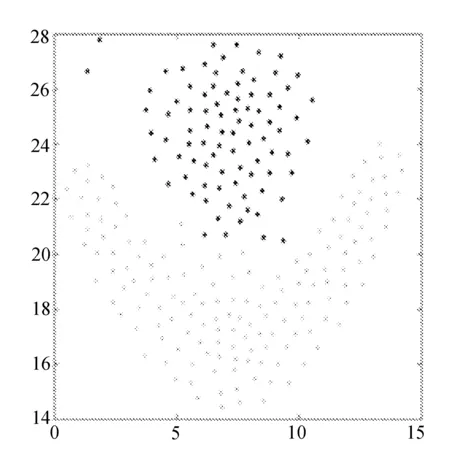
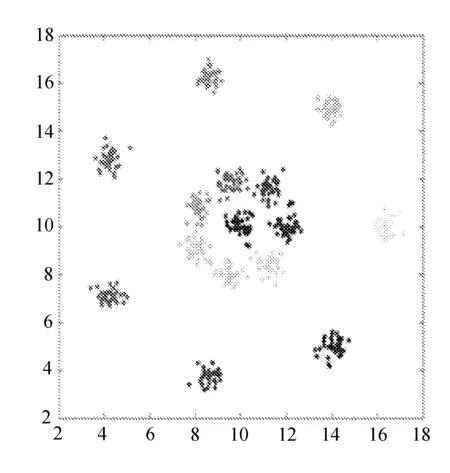
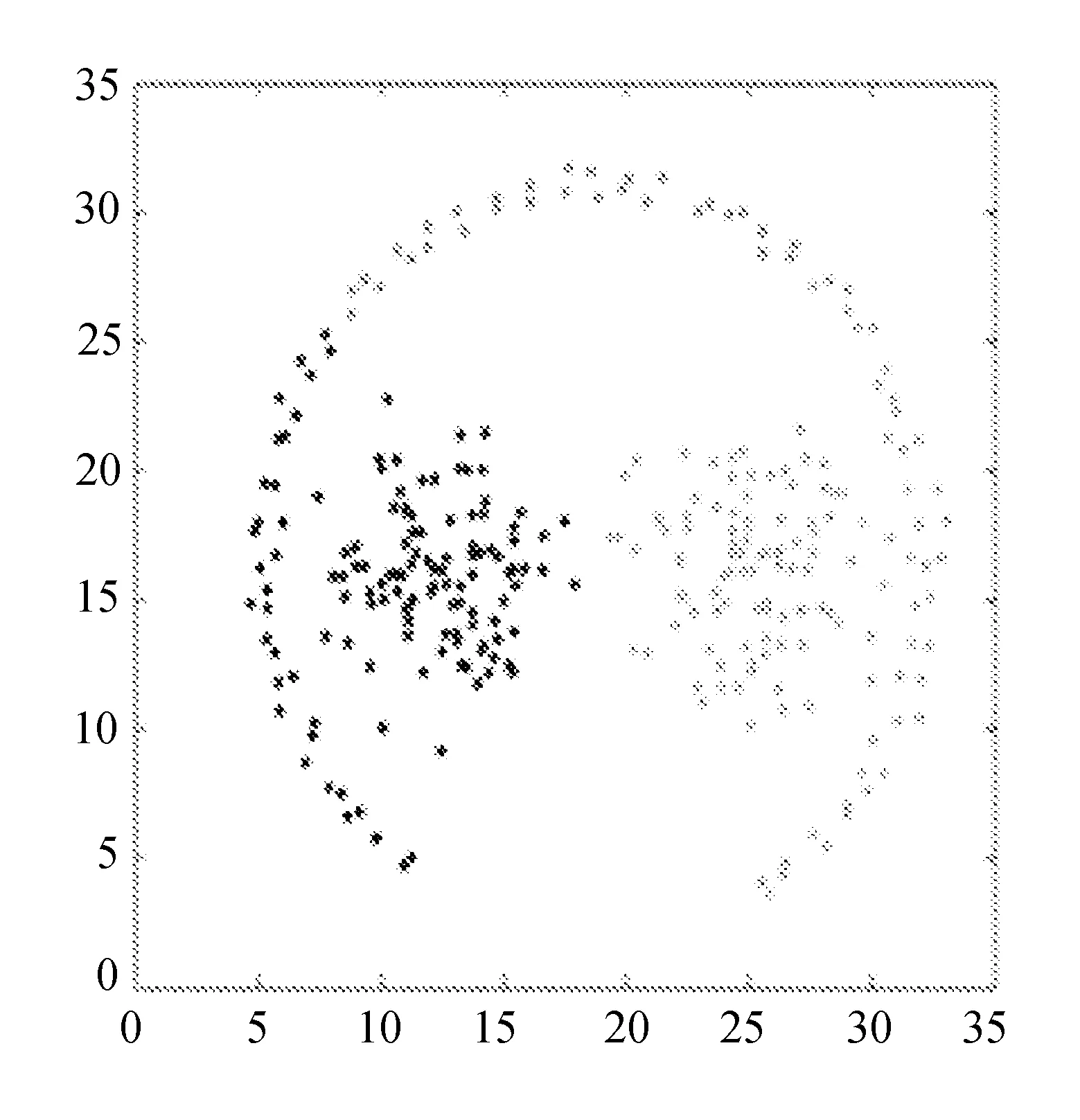
Flame、Pathbased、R15和D31等数据集的聚类结果二维图分别如图1～图4所示。

(a) DPC,dc=3%,1.133 6

(b) CS-DPC,dc=0.493 8

图1 Flame聚类结果

(a) DPC,dc=3%,0.472 6

(a) DPC,dc=3%,1.897

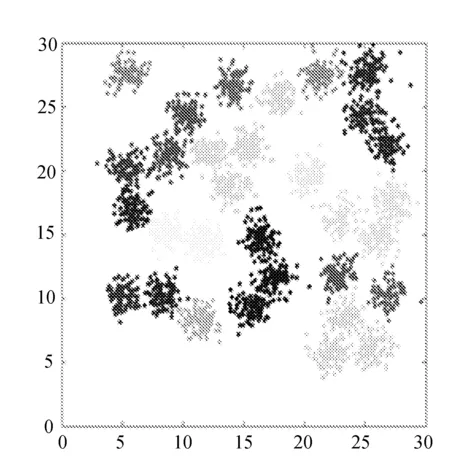
(a) DPC,dc=3%,1.990 0

对于数据集Flame、R15、Pathbased，CS-DPC算法可以达到DPC算法的聚类效果，并且对于数据集D31，CS-DPC算法聚类效果要优于DPC算法。

聚类结果对比如图5所示。

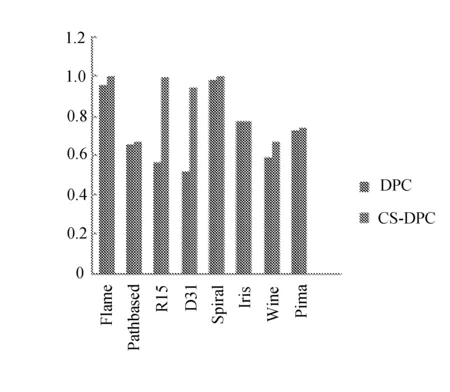
(a) Silhouette指标对比

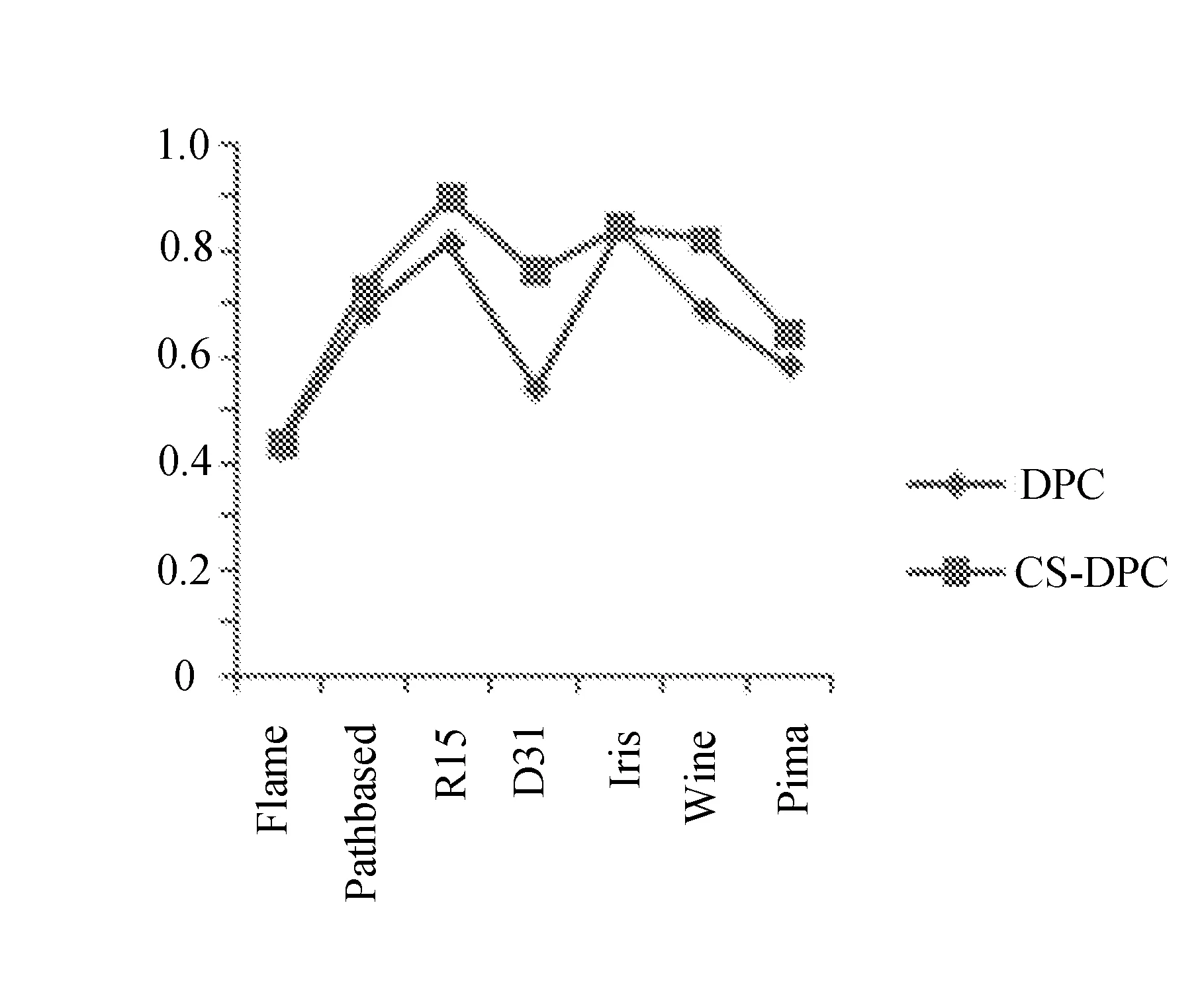
(b) F-measure指标对比

图5 聚类结果对比图

图5(a)清晰地表明，CS-DPC算法聚类结果的内部指标与DPC算法对比,无论二维还是多维数据集，CS-DPC算法聚类结果准确度相对于DPC算法都提高很多。图5(b)表明，CS-DPC算法聚类结果准确度比DPC算法聚类结果准确度更高。

4 结 语

密度峰值快速搜索聚类算法是一种基于密度的聚类算法，基本原理类似均值偏移理论和K中心聚类算法。相比较其他聚类算法，DPC算法具有简单高效的特点。布谷鸟算法利用布谷鸟特殊的繁育寄生机理和Levy飞行搜索机制，模拟出布谷鸟寻窝产卵行为的一种群体智能优化算法。其具有参数少、逻辑结构简单、全局搜索能力强等优点,目前已经成功用于求解多种工程优化问题。CS算法凭借Levy飞行随机游动和偏好游动策略，在求解优化问题时具有较好性能。基于CS算法全局搜索能力和局部快速搜索的优势，提出布谷鸟优化的密度峰值快速搜索聚类(CS-DPC)算法，解决DPC算法需手动给出截断距离dc的缺陷。改进的算法引入方向因子解决两个聚类中间部分数据划分问题。通过5个人工数据集和3个标准UCI数据集实验仿真，采用内部评价指标Silhouette和外部评价指标F-measure验证两个聚类结果的有效性。实验结果表明，CS-DPC算法的聚类结果和准确度均优于DPC算法。

参考文献：

[1] Xu R， C Wunsch D. Survey of clustering algorithms[J]. IEEE Transactions on Neural Networks,2005,16：645-678.

[2] J Frey B， Dueck D. Clustering by passing messages between data points[J]. Science，2007，315:972-976.

[3] 胡明,唐东凯,李芬田,等.不确定聚类中距离计算方法综述[J].长春工业大学学报,2017,38(5):477-483.

[4] Frey B J, Dueck D. Clustering by passing messages between data points[J]. Science,2007,315:972-976.

[5] Xu R, Wunsch D. Survey of clustering algorithms[J]. IEEE Trans Neural Netw Learn Syst.,2005,16:645-678.

[6] Sambasivam S, Theodosopoulos N. Advanced data clustering methods of mining Web documents[J]. Issues in Informing Science and Information Technology,2006(3):563-579.

[7] Rodriguez A, Laio A. Clustering by fast search and find of density peaks[J]. Science,2014,344:1492-1496.

[8] Cheng Y. Mean shift, mode seeking and clustering[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence，1995，17:790-799.

[9] Kaufman L, JRousseeuw P. Finding groups in data: An introduction to cluster analysis[M]. [s.l.]:DBLP,1990.

[10] Du M, Ding S, Jia H. Study on density peaks clustering based on k-nearest neighbors and principal component analysis[J]. Knowledge Based Systems,2016,99：135-145.

[11] Wang M, Zuo W， Wang Y. An improved density peaks-based clustering method for social circle discovery in social networks[J]. Neurocomputing，2016，179:219-227.

[12] Aksehirli E, Goethals B, Muller E. Efficient cluster detection by ordered neighborhoods[C]// In Big Data Analytics and Knowledge Discovery.2015:15-27.

[13] Chen Y, Lai D, Qi H, et al. A new method to estimate ages of facial image for large database[J]. Multimedia Tools and Applications,2015(2):1-19.

[14] Li Y, Liu W, Wang Y. Co-spectral clustering based density peak[C]//In 2015 IEEE 16th International Conference on Communication Technology (ICCT).2015:925-929.

[15] Jia S, Tang G, Hu J. Band selection of hyperspectral imagery using a weighted fast density peak-based clustering approach[C]//In Intelligence Science and Big Data Engineering. Image and Video Data Engineering.2015:50-59.

[16] Xie K, Wu J, Yang W, et al. K-means clustering based on density for scene image classification[C]//Proceedings of the 2015 Chinese Intelligent Automation Conference.2015:379-386.

[17] Zhang W, Li J. Extended fast search clustering algorithm: widely density clusters, no density peaks[C]// Computer Science,2015.

[18] Aksehirli E, Goethals B, Muller E. Efcient cluster detection by ordered neighborhoods[C]//In Big Data Analytics and Knowledge Discovery.2015:15-27.

[19] Chen Y, Lai D, Qi H, et al. A new method to estimate ages of facial image for large database[C]//Multimedia Tools and Applications.2015:1-19.

[20] Jia S, Tang G, Hu J. Band selection of hyperspectral imagery using a weighted fast density peak-based clustering approach[C]//Intelligence Science and Big Data Engineering. Image and Video Data Engineering,2015:50-59.

[21] Yang X, Deb S. Cuckoo search via L’evy flights[C]//Proceedings of the World Congress on Nature and Biologically Inspired Computing (NABIC’09). [S.l.]: IEEE, 2009:210-214.