函数解析式求法的探讨

广西贺州市平桂区平桂高级中学 龚卫华

一、换元法

例1 已知：

解：原函数可化为

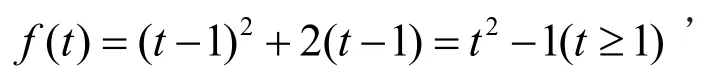
把中t换成x，得

评述：已知是关于x的函数，即求的解析式，通常令。由此解出将代入中，求得的解析式，再用x替换t，便得的解式。注意，换元后要确定新元t的取值范围。

二、配凑法

根据具体解析式凑出复合变量的形式，从而求出解析式。

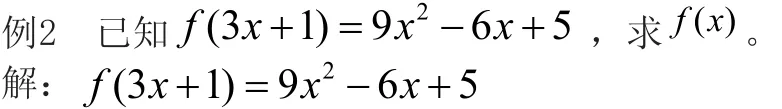
评述：复合变量的值域就是的定义域。

三、待定系数法

根据已知条件识出一个含有待定系数的代数式或函数式或方程，然后利用恒等式的性质，或得已知条件代入，建立方程（组），通过解方程（组）而求出待定系数的值，或者消除这些待定系数，找出原来那些已知系数间存在的关系，这种方法叫待定系数法。

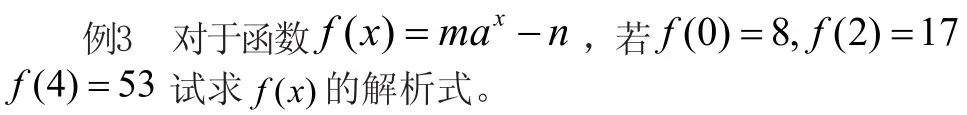
评述：当能确定未知函数是何类型系数时，常用待定系数法求出这个函数。

四、消参法

五、迭加（乘）法

评述：迭加（乘）法实际上即求数列通项公式的方法。

六、数学归纳法

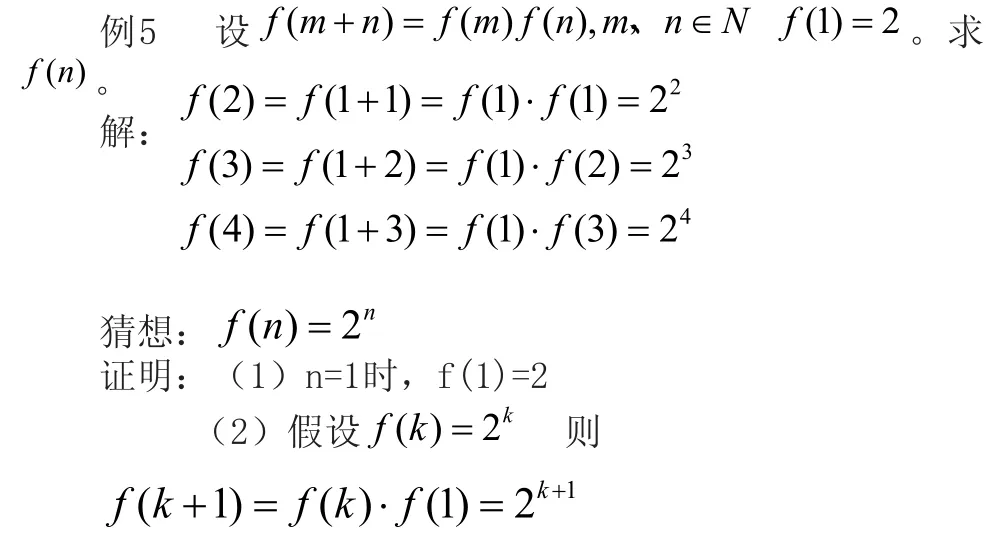
综合（1）（2）猜想成立。

评述：方法五、六均为求数列通项公式的方法。求数列通项的方法也可归为求函数解析式的方法，由于篇幅所限，不一一赘述，仅以五、六为代表。

七、伴生式方程组法

八、赋值法

评述：已知条件是抽象函数时，可考虑用赋值法。

九、区间变换法

评述：求函数解析式方法多样，其中“配凑法”“换元法”“待定系数法”“区间变换法”应重点掌握。