近几年高考中的识图问题

河北省承德市宽城满族自治县第一中学 韩晓锋

函数是中学数学的重要内容，函数的图像在函数的学习中起着重要的作用。函数所具有的性质在其图像上必有直观的体现；图像所具有的特点在其解析式上必有反映，所以我们既要借助于函数解析式中某些数的精确性又要借助图像的几何直观性、形象性来揭示函数式中的某种关系，这深刻体现了数学中数形结合的重要思想方法。因此，函数图像一直是多年高考的热点之一。

在识图方面的考查，一般是已知函数解析式，选择合适的图像。这是近几年高考中考察图像问题的一种非常流行的方式。这种问题一般都是给出函数解析式，然后从四个选项中选择一个与之匹配的图像。

【2013课标1，文9】函数f(x)=(1－cosx)sinx在[－π，π]的图像大致为( )

解：根据题意可以知道：

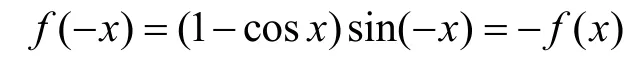
故函数()fx为奇函数，可排除B，

有因为当 x∈(0,π)，1- cosx ＞ 0,sinx＞0，故 f( x)＞0，可排除A，又

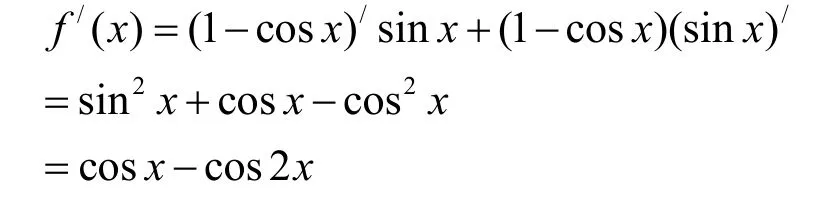
所以C选项是正确的。

本题考查了三角函数图像，在平时学习中要加强这方面的练习，在考试时灵活的应用，并能很快得到正确答案。

短短几十分钟车程，听了这几个起伏跌宕、诡谲奇特的故事，是不是能归纳出一些人生智慧呢？坐霸王车赖账的事，相对简单。长程载客，先收点油钱自保，该是行规，也是常识。队长遇上武林高手的事，也不算怪，对乡下来的长者，他不但没有包容体谅，反而唠叨欺生，受了教训，也是自找。而且，因此改变待人处世的态度，长远来看是好事。

【2014课标1，理6】如图，圆O的半径为1，A是圆上的定点，P是圆上的动点，角x的始边为射线OA，终边为射线OP，过点P作直线OA的垂线，垂足为M，将点M到直线OP的距离表示为x的函数()fx，则y=()fx在[0,π]上的图像大致为

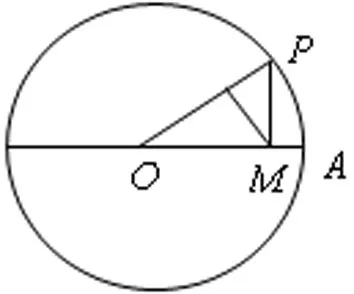
解：当时，OM=1· cosx=cos x，则点M到直线OP的距离

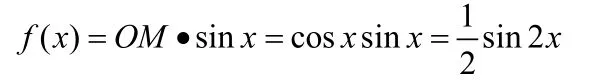
当时，OM=1·c os(π- x)=-cosx，则点M到直线OP的距离

综上所述，y=f( x)在[0 ,π ]上的解析式为

其图像如C所示。

本题主要考查了三角函数的基本性质。

【2016高考新课标1文9理7】函数在[-2,2]的图像大致为（ ）

解：函数在[0,2]上是偶函数，其图像关于y轴对称。因为f(2)=8-e2,0＜8-e2＜1,所以排除A，B选项；当x∈[0,2]时，y/=4x-ex有一零点，设为 x0，当x∈(0 ,x0)时，f( x)为减函数，当x∈(0,2)时，f( x)为增函数，故选D。

本题考察的知识点是函数的图像，对于超越函数的图像，一般采用排除法解答。

【2017课标1，文8】函数的部分图像大致为

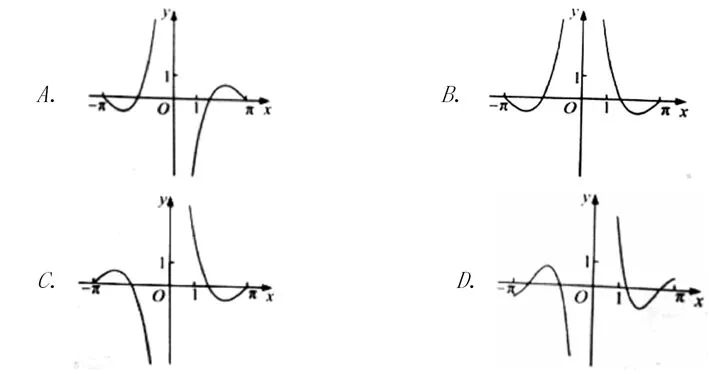
解：由题意知，函数为奇函数，故排除B；当xπ=时，0y=，排除D；当X=1时，，排除A，故选C。

函数图像问题首先关注定义域，从图象的对称性，分析函数的奇偶性，根据函数的奇偶性排除部分选择支，从图象的最高点、最低点，分析函数的最值、极值利用特值检验，较难的需要研究单调性、极值等，从图象的走向趋势，分析函数的单调性、周期性等确定图象.

总结：对于给出解析式选择图像的问题，可以运用排除法。根据图以识别函数所具有的一些性质。比如奇偶性、对称性、周期性等，还要看图像的最高点、最低点、是否过原点或其他特殊点等，根据这些特征排除选项。可以按以下步骤；

（1）从函数的定义域，判断图像的左右位置；从函数的值域，判断函数的上下位置；

（2）从函数的单调性，判断函数的变化趋势；

（3）从函数的奇偶性，判断图像的对称性，如奇函数在对称的区间上单调性一致，偶函数在对称的区间上单调性相反；

（4）从函数的周期性，判断图像的循环往复；

（5）从特殊点出发，排除不符合要求的选项。

灵活应用上述方法，可以很快选择出正确的函数图像。