基于数据分解的高速QPSK并行解调方法

闫 迪, 王元钦, 吴 涛, 孙 克

(1. 航天工程大学电子与光学工程系, 北京 101416; 2. 北京航天飞行控制中心, 北京 102206)

0 引 言

数据中继卫星、遥感侦察卫星和空间合成孔径雷达对实时海量数据传输提出了越来越高的要求。美国国家航空航天局的同步航天器到地面的数据传输速率在2008年达到了800 Msps,预计2020年将达到100 Gbps[1-3]。目前,高速数传调制体制主要以多进制数字相位调制为主[4-5],由于现场可编程门阵列(field programmable gate array,FPGA)速率的限制,为了提高解调速率,必然采用并行解调方式。目前,唯一公布的并行处理架构是并行接收结构(parallel receiver,PRX)和全数字并行接收结构(all-digital parallel receiver,APRX)[6]。基于APRX架构,文献[7]于2008年完成了800 Mbps固定速率的8进制相移键控解调样机。文献[8]于2011年完成了1.5 Gbps的16进制正交振幅调制解调器。APRX结构要求采样率必须为数据率的整数倍,信号中心频率随数据率选取,而在实际工程中,中频频率和采样率多为固定值。在卫星通信等高动态应用背景下,多普勒效应带来的数据率多普勒变化范围大,为了保证采样率和数据率的整数倍关系,需要在采样模块后增加内插器,目前没有在文献中找到相关做法。可见,APRX架构存在数据率不灵活的缺点。

通用处理器最大的优势是核心多,拥有大量计算资源,可以实现多线程的并行处理。2016年9月,英特尔发布的基于众核心架构的新型XeonPhi7200系列众核处理器,代号Knights Landing[9],最多72核心288线程,主频为1.5 GHz。同年,英伟达发布的Tesla P100 计算卡[10],拥有3 584个处理核心,核心频率达1 328 MHz。大量的核心资源使得基于通用处理器的高速数字信号处理成为可能[11-13]。目前,相关研究主要有开源项目GNU Radio软件无线电平台[14-15],微软亚洲研究院开发的Sora平台[16],两个平台均使用软件流水线的方法,把数字调制问题转化为软件编程问题。流水线这种并行处理方法依赖中央处理器(central processing unit,CPU)的高主频,没有充分发挥多核CPU的计算能力,GNU Radio的处理速率只可以实现几十kbps,Sora达到的实时通信速率也只有43.8 Mbit/s。显然,无法基于这两种平台实现高速数字信号处理。

本文提出一种适用于通用处理器平台的高速正交相移键控(quadrature phase shift keying,QPSK)并行解调方法,具有以下3个特点:

(1) 高可用性

每个信号块的解调处理是独立的,如果某个解调进程意外终止,既不影响其他解调进程的运行,也能将未处理的信号块转移到其他解调进程,大大提高了本方法的可用性。

(2) 适用于任意数据率

在APRX框架上研制的解调器存在数据率不灵活的缺点,本方法可适用于任意数据率。

(3) 强伸缩性

本方法的实际解调速率取决于解调进程的数目,所以通过扩展计算资源可实现解调速率的近似线性提高。

该方法由并行处理框架和并行解调算法组成。并行解调框架基于数据分解的并行化思想,将中频数字采样后的数字信号按时间顺序分解为信号块,利用多核CPU的多线程处理能力,对信号块进行并行解调。本文在最大似然(maximum likelihood,ML)估计的基础上,提出了一种基于三维迭代搜索的QPSK开环解调算法,该算法具有以下3个特点:

(1) 利用分段积累求相关值的方法消除了调制信息的影响;

(2) 同时完成了载波同步和码元同步;

(3) 用迭代搜索方法,不断缩小载波参数搜索范围,在保证载波参数估计精度的同时降低了计算量。

1 并行解调方法框架

由于传统解调算法存在任务串行和数据串行缺点,故提出了一种基于数据分解的并行解调框架,将通用处理器的多核心优势转化为高速数字信号的解调能力。并行解调框架由3部分组成:信号分割、信号处理和结果综合,如图1所示。

(1) 信号分割

信号分割的功能是把一维串行数字信号分解成多路信号块。涉及到的参数是信号块长度L,L由解调算法决定。如果在L时间内,QPSK载波频率的变化量小到一定程度,就可以把载波同步问题转化为关于载波频率和载波初相的参数估计问题。后文将对L的设计方法进行研究。

(2) 信号处理

信号处理的功能是对信号块进行多路并行解调,由多个解调进程组成,每个解调进程的处理程序完全相同,只有输入数据不同。QPSK的常用解调方法是科斯塔斯环,科斯塔斯环是一种相干解调方法,其原理是在本地构造与QPSK同频同相的载波,载波与QPSK混频后的低频信号就是基带信号。科斯塔斯环是典型的串行算法,前后信号处理存在依赖性,不适用于本文提出的并行处理框架,后文将对开环解调算法进行研究。

(3) 结果综合

结果综合的功能是把多路解调结果综合处理,形成最终解调结果。本地载波与QPSK的相位差存在4种模糊,各信号块独立解调,导致模糊不一致。在综合各信号块的解调结果时,要去除这种不一致性,后文将对相位模糊的一致性方法进行研究。

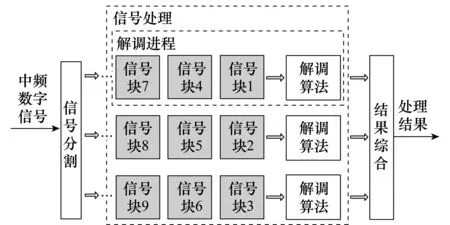
图1 并行解调方法框架Fig.1 Parallel demodulation method framework

2 信号块长度分析

本文解调算法通过对QPSK载波频率和载波初相进行估计,得到同频同相载波,其前提是QPSK的载波频率是定值。实际情况中载波频率是有多普勒变化的,对信号块长度L产生了约束,若L太大,会发生基带信号极性翻转。因此,需要对L进行约束分析。

设接收信号载波频率fc(t)按线性规律变化,即fc(t)=f0+f1t,其中f1是一阶变化率,单位是Hz/s,载波频率估计值是fn。为了防止基带信号发生极性翻转,必须保证

(1)

设载波频率按线性规律变化,即fc(t)=f0+f1t,其中f1是一阶变化率,单位是Hz/s。那么,式(1)可化简为

ΔfL+0.5f1L2<0.25

(2)

式中,Δf=f0-fn是载波频率估计精度。通过式(2)可大致估算出L,即

(3)

3 开环解调算法

3.1 算法原理

QPSK解调中最重要的部分是载波同步,载波同步技术分为两类:一类是基于锁相环理论的闭环反馈同步技术,另一类是基于ML的开环前馈同步技术。传统的解调算法一般采用锁相环的方法,存在挂起现象,建立同步时间较长。本文的并行解调方法使用开环解调算法,处理速度快,适用于短信号块的处理。基于ML的开环解调算法存在去除调制信息问题,分为数据辅助法和非数据辅助法。

(1) 数据辅助法[17]

这种方法在每个信息帧前加入一段已知的前导码,降低了信息传输效率。本文将连续的信号分解为较短的信号块,即使存在前导码,也无法保证每个信号块内均存在前导码。

(2) 非数据辅助法[18]

这种方法通过非线性变换法和M次倍频法去除调制信息,但都有一定的处理增益损失。在低信噪比情况下,其恶化影响更严重。经理论分析,平方倍频带来的信噪比损失高达9 dB。

本文在ML基础上,提出一种基于三维迭代搜索的QPSK解调算法。算法基本原理是在〈载波频率,载波初相〉二维区间上,通过搜索QPSK信号与本地载波的最大相关值,得到QPSK信号的载波频率和初相估值。为消除调制信息对相关值的影响,使用一种分段积累求积分的方法,同时得到第一个码元的起始时刻。所以这种算法本质上是对QPSK信号的3个参数〈载波频率,载波初相,第一个码元起始时刻〉进行估计,称之为“三维搜索”。通过迭代搜索,逐步缩小搜索区间,减小搜索步长,达到降低计算量的目的,故称为“迭代搜索”。算法流程如图2所示,详细步骤如下。

步骤1初始化搜索区间

初始化搜索区间〈fn(i),φn(j),m〉p,其中,fn(i)是载波频率,个数是Nf;φn(j)是载波初相,个数是Nφ;m∈[1,L0]是第一个码元起始时刻;下标p=0表示迭代次数为0。

步骤2构造本地载波

根据〈fn(i),φn(j),m〉p构造本地载波信号locali,j(k)。

(4)

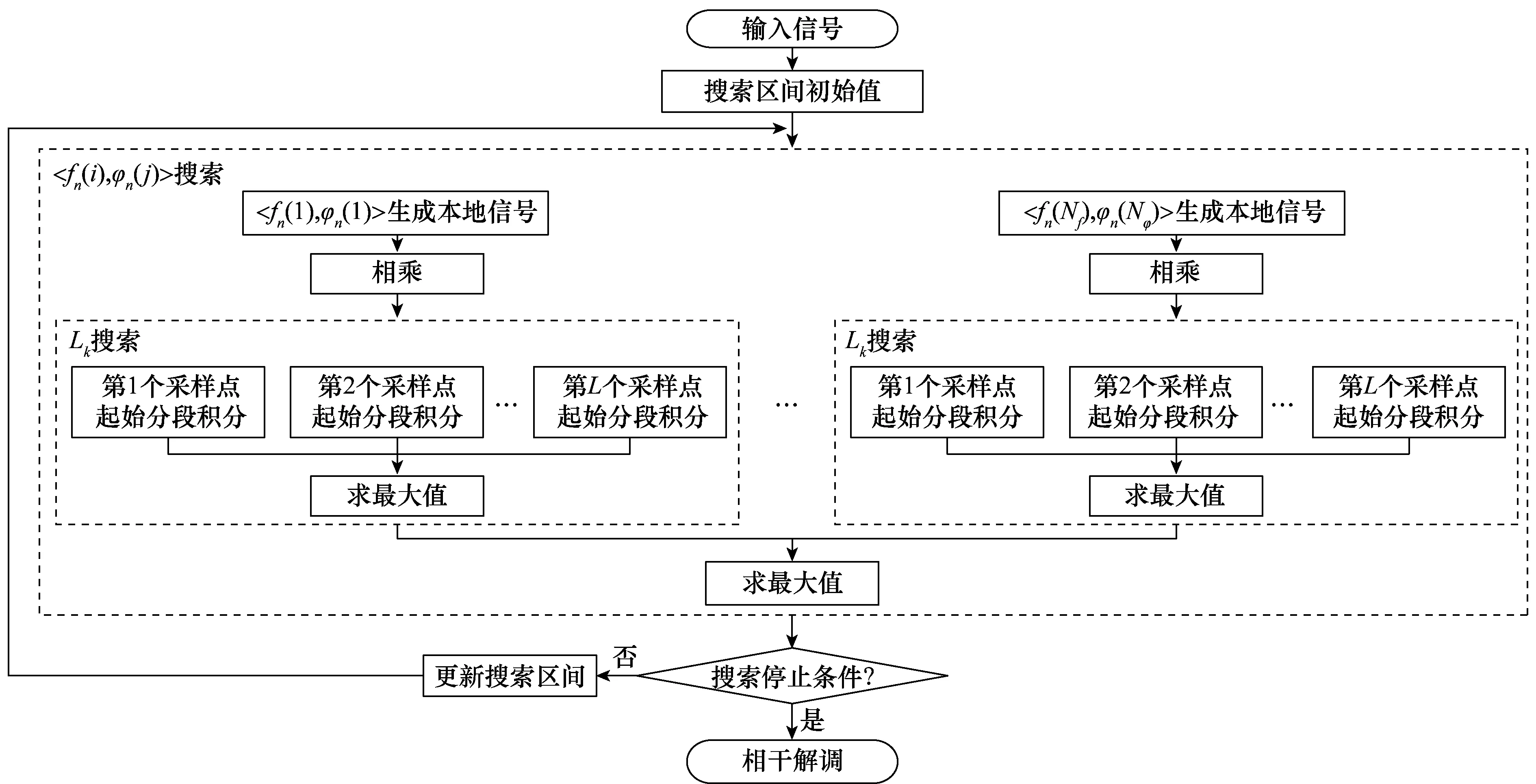
图2 开环解调算法流程图Fig.2 Flow chart of open loop demodulation algorithm

步骤3求相关值

对每个本地载波信号,与信号块相乘,得到如式(5)所示的混频信号mixi,j(k)。对每个混频信号mixi,j(k)进行分段积累,得CORRi,j,m。设第一个码元的起始采样点是第m个采样点,那么积分值CORRi,j,m求法如图3所示。

mixi,j(k)=locali,j(k)×x(k)

(5)

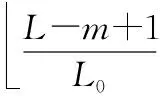
(6)

步骤4参数估计

对于Nφ×Nf个混频信号mixi,j(k),求其所有相关值CORRi,j,m的最大值,就是相关值EstCORRi,j,其对应的fn(i),φn(j),m就是载波参数的估计值。

(7)

图3 分段积累的计算方法Fig.3 Calculation method of segmentation integral

步骤5更新搜索区间

当〈fn(i),φn(j),m〉p满足迭代停止条件时,利用估计值进行相干解调；当〈fn(i),φn(j),m〉p不满足迭代停止条件时,更新搜索区间〈fn(i),φn(j),m〉p+1,返回到步骤2。满足以下三者中的任意一个即可停止迭代:

(1) 本次迭代的相关值小于上次迭代;

(2) 〈fn(i),φn(j),m〉p内载波频率的步长小于50 Hz;

(3) 〈fn(i),φn(j),m〉p内载波初相的步长小于0.01。

根据经验,搜索区间的更新方法是:对第p次迭代得到的fn(i),φn(j),分别取其左右相邻值作为p+1次迭代搜索区间的边界值,步长缩小为第p次步长的1/3,m值的区间不变化。

3.2 算法复杂度分析

首先对单次迭代搜索的计算量进行分析,单次迭代搜索的计算量主要是构造搜索信号和分段相关计算。构造搜索信号的计算经过优化后,可由L次相位累加和L次求余弦组成。在N1×N2×N3次分段相关计算中,共有N1×N3次确定码元分布计算,每次码元分布计算包含L次加法;共有N1×N2×N3次积分计算,每次积分计算包含L次加法。因此,单次迭代搜索计算量为N1×N2×N3×2L+N1×N3×L+N1×N2×N3×L。大量仿真表明,在4次迭代内基本能完成参数估计,故算法的计算量是K×L,其中K=12×N1×N2×N3+4×N1×N3。

4 相位模糊一致性方法

4.1 信号块之间的相位模糊

在科斯塔斯环方法中,本地恢复载波与接收QPSK载波的相位差有4种可能:0,0.5π,π,1.5π,从而导致解调结果存在4种模糊[19]。假设本地载波与QPSK载波同频,只存在相位差Δφ,本地同相、正交载波与QPSK混频后,得到低频信号

(8)

Δφ的4种模糊对I、Q路解调比特流a(k)、b(k)的影响如表1所示。

表1 QPSK解调的相位模糊

对于本文的每个信号块而言,同样存在这种模糊现象,除此之外,信号块的独立解调引起了各信号块的模糊不一致。在使用传统方法进行解模糊之前,首先要消除各信号块的模糊不一致性。本文提出了一种基于数据冗余的相位模糊一致性方法,利用相邻两个信号块的冗余重叠,消除模糊的不一致性。

4.2 基于数据冗余的相位模糊一致性方法

本方法的基本思想是利用信号冗余分割,使相邻信号块存在一定长度的重叠,利用重叠区的比特流进行相位模糊调整。图4为信号冗余分割方法,L为信号块长度,L0为信号块重叠区长度。

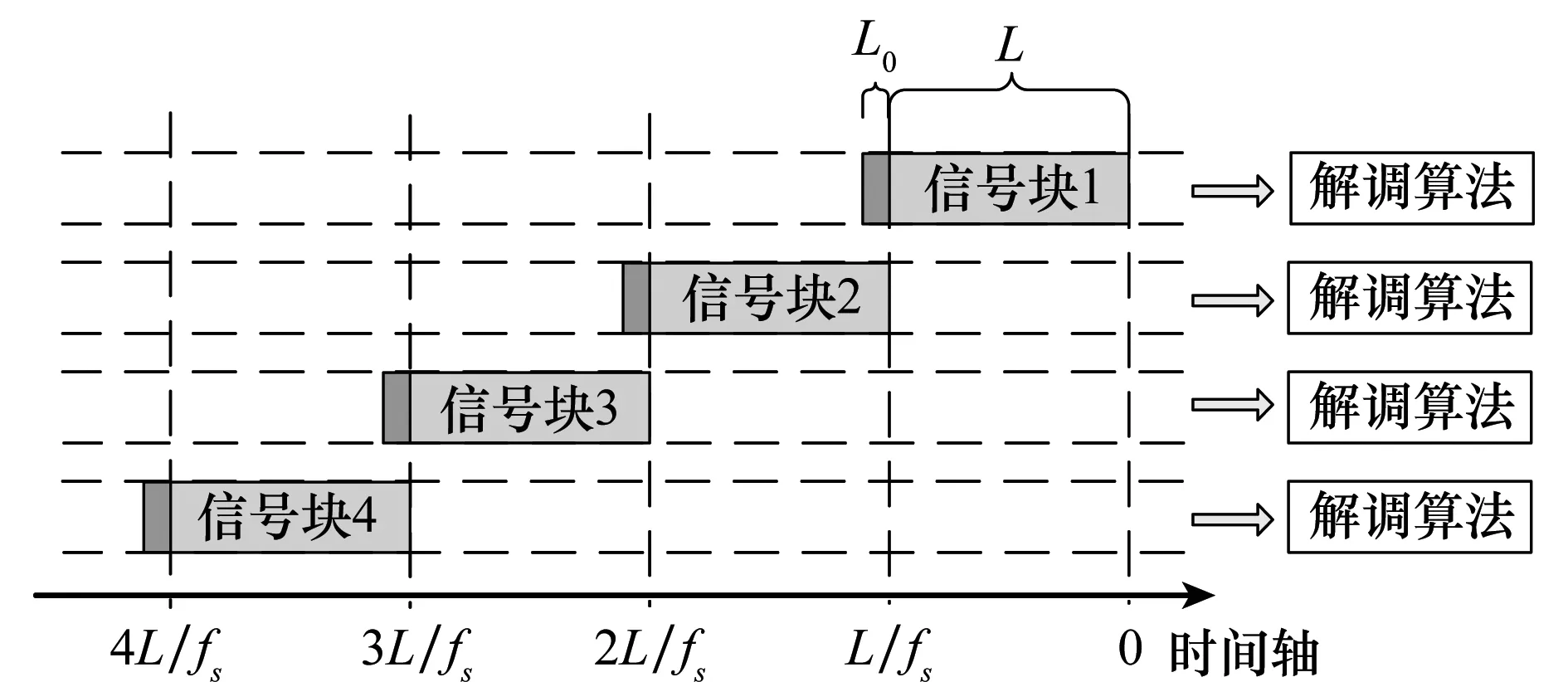
图4 信号冗余分割方法Fig.4 Redundancy segmentation method of signal

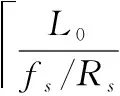
步骤1I路匹配

Ibit_last分别与Ibit、-Ibit、Qbit和-Qbit进行匹配,得到匹配结果和重叠比特数。以Ibit为例,对于每一个Nbit取值,分别求出Ibit_last末尾Nbit个比特与Ibit起始Nbit个比特的欧几里得距离d,如式(9)所示。如果d=0,则匹配成功,同时得到了重叠比特数,否则匹配不成功。

(9)

步骤2I路更新

用与Ibit_last匹配成功的解调结果对Ibit_last进行更新,并输出Ibit_last。

步骤3Q路处理

用步骤1和步骤2中的方法对Qbit_last进行处理,输出Qbit_last。

步骤4对下一信号块进行处理。

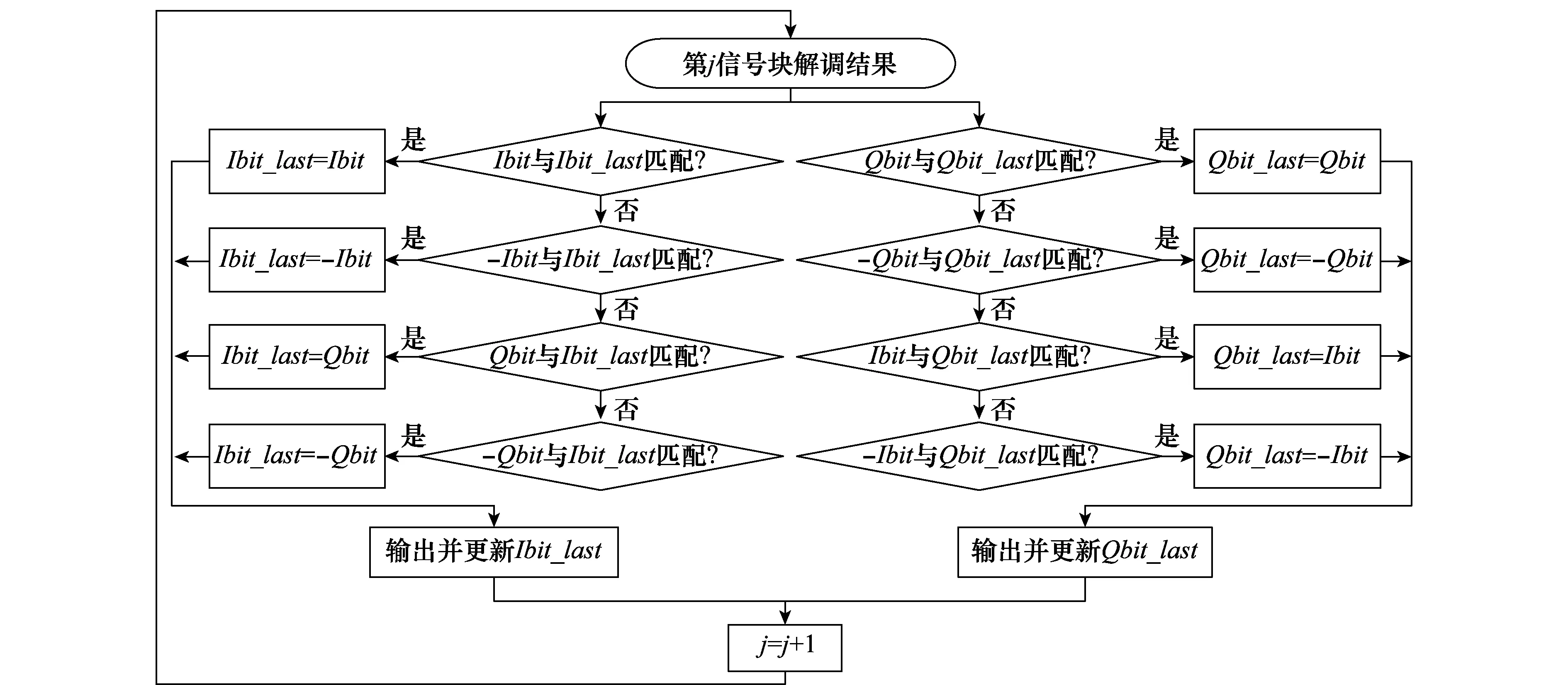
图5 相位模糊一致性方法流程图Fig.5 Flow chart of phase ambiguity consensus method

5 对比分析与仿真测试

5.1 与APRX方法的对比分析

APRX是目前唯一公布并被大量采用的并行全数字接收机设计方案。本文方法与APRX方法相比,具有以下3点不同:

(1) 同步原理不同

APRX结构上的载波、符号同步原理是基于锁相环理论。本文方法是把连续时间上的同步问题转化为短时间的参数估计问题,利用估计参数构造本地载波,是一种迭代搜索的ML方法。

(2) 并行原理不同

APRX将高速率信号串并转换为多路低速率信号,完成并行频域匹配滤波得到基带信号,继而进行并行载波、符号同步。并行载波同步环路采用并行处理方法,通过并行提取一帧(N点)的频率误差,然后进行并行环路滤波产生控制字,并行码元同步环路也是此原理[20]。本文方法是将连续信号拆分为信号块,利用多进程并行方法同时对多信号块进行处理。在每个信号块处理任务中,需要大量的相关运算,利用多线程方法同时进行多个相关运算。

(3) 适用平台不同

APRX适用于FPGA平台,如果在CPU和通用计算图形处理器(general purpose graphics processing unit,GPGPU)的异构平台上实现,需要数据反馈和大量线程同步,必然带来性能下降。本文方法需要大量计算资源,适用于CPU-GPGPU平台,而不适用于FPGA平台。

5.2 算法仿真

本节对本文提出的方法进行仿真,统一设置仿真参数为:QPSK信号码率Rb=2 Gbps;载频频率fc=1 GHz;采样频率是fs=4 GHz;多普勒频率fd=12 345 GHz;载波初相φc=0.40 rad;码元起始时刻是第2个采样点。

5.2.1 分段积累方法的仿真结果

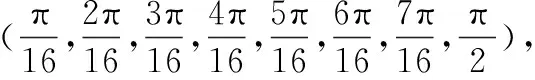
图6是采用分段积累方法的搜索结果,为了表示方便,没有画出m维,在多普勒12 000 Hz,载波初相0.39 rad时取得最大相关值39 930,搜索结果是正确的。取12 000 Hz,0.39 rad,对不同m值下的分段积分进行仿真,结果如图7所示,在m=4时,取得最大相关值,可见对码元起始时刻的搜索结果是正确的。图8是采用普通相关方法的搜索结果,在载波多普勒20 000 Hz,载波初相1.57 rad时取得最大相关值501,搜索结果是错误的。

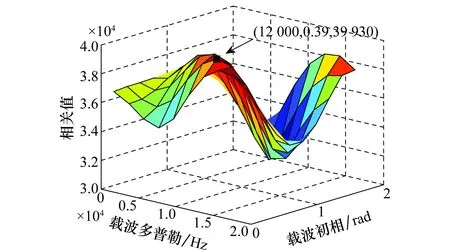
图6 分段积累方法的搜索结果Fig.6 Search results of segmentation integral method

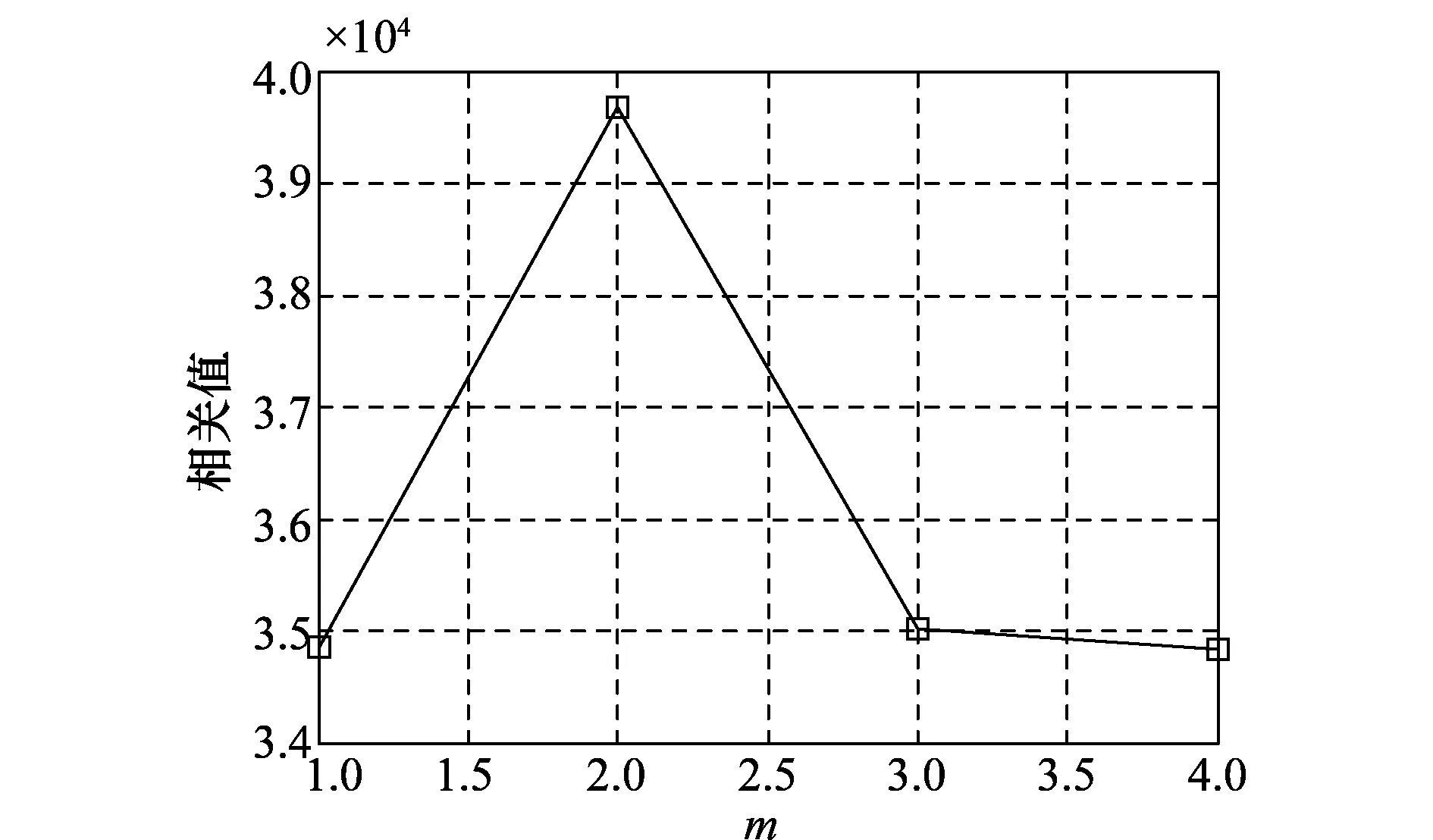
图7 不同m值下的相关值Fig.7 Correlation values of different m values

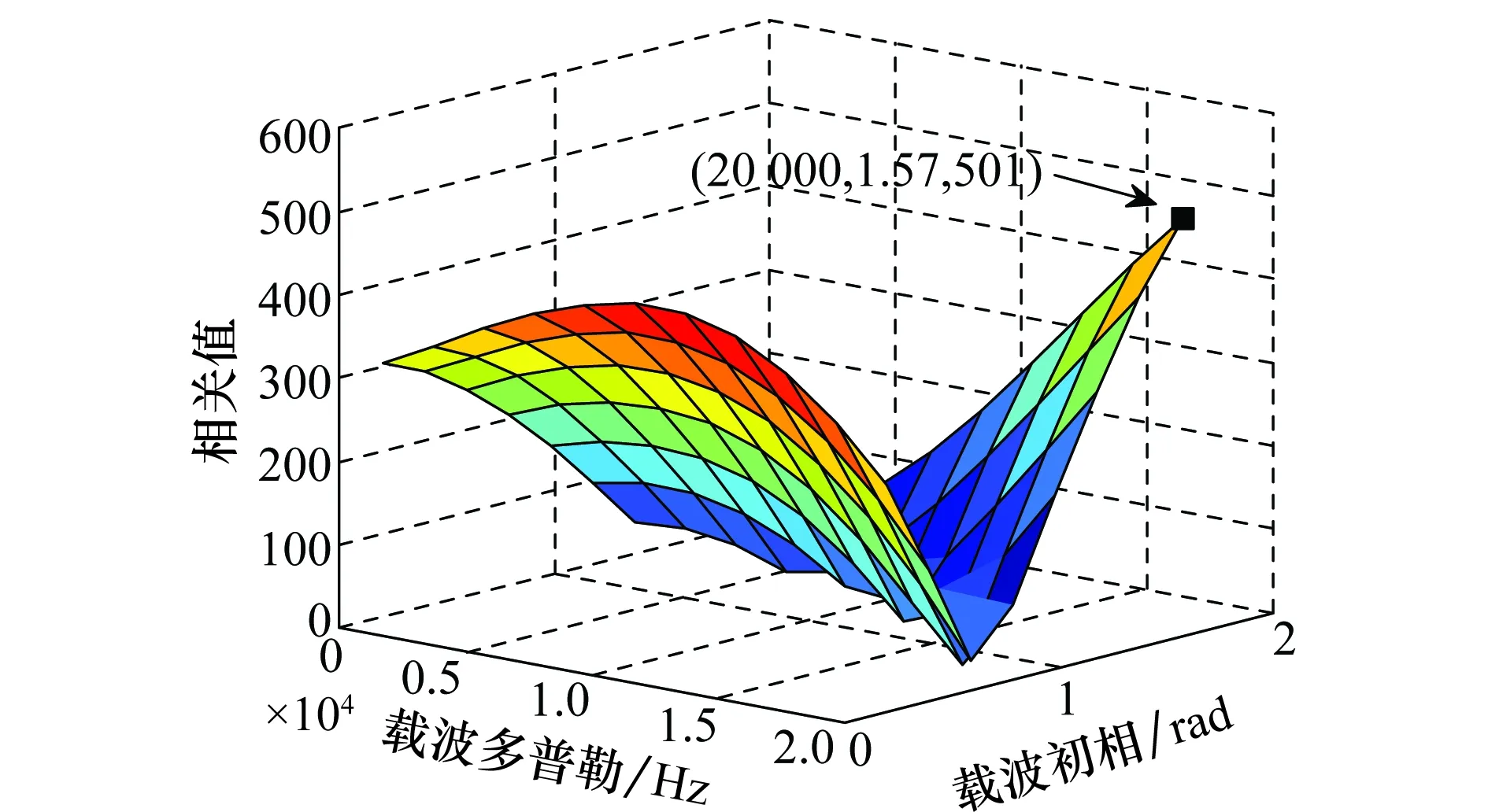
图8 普通相关方法的搜索结果Fig.8 Search results of correlation method

5.2.2 三维迭代搜索算法的仿真结果

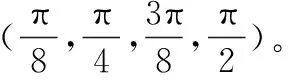
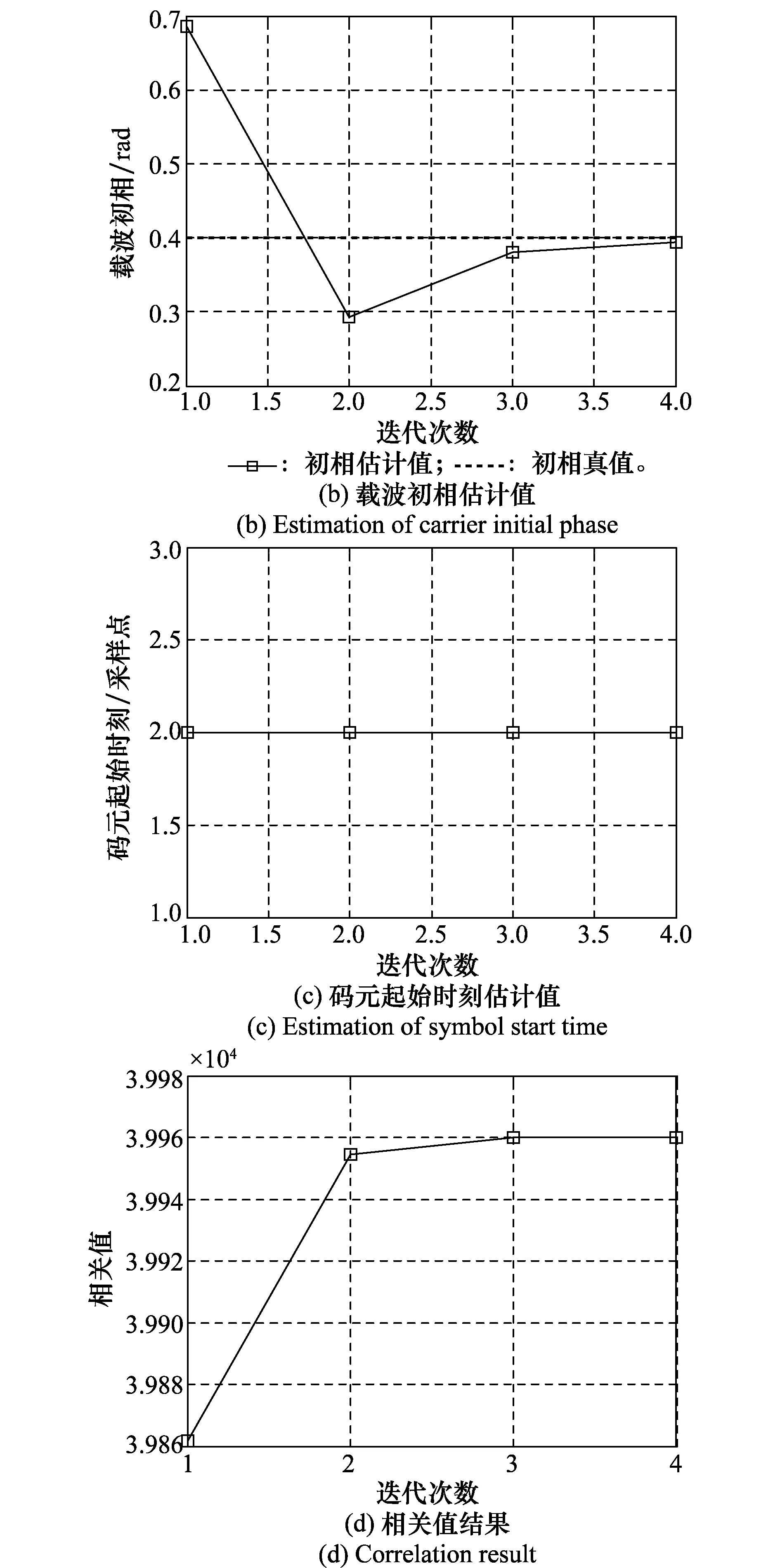
图9 三维迭代搜索算法的仿真结果Fig.9 Results of three dimentional iterative search algorithm

5.2.3 误码率仿真结果

用本文的并行解调方法,对QPSK信号进行解调,统计误码率结果与克拉美罗下界(Cramer-Rao lower bound, CRLB)如图10所示。由仿真结果可得,本文方法的解调信噪比损失在0.1 dB以内。

5.3 算法解调速度测试

为了进一步验证本文算法的可行性和解调速度,在CPU-GPGPU异构平台上搭建验证系统。验证系统由调制机和解调机两部分组成,二者之间通过万兆网连接,调制机产生8 bit量化的QPSK信号后,直接传给解调机进行处理,略去数模转换和模数转换环节。调制机采用“多线程计算,轮流输出”的方法,利用多线程并行计算能力,每个线程产生时间上间隔的QPSK信号块,然后按顺序轮流读取各线程产生的信号块,就得到了时间上连续的QPSK信号流。系统配置如表2所示,系统实物如图11所示。

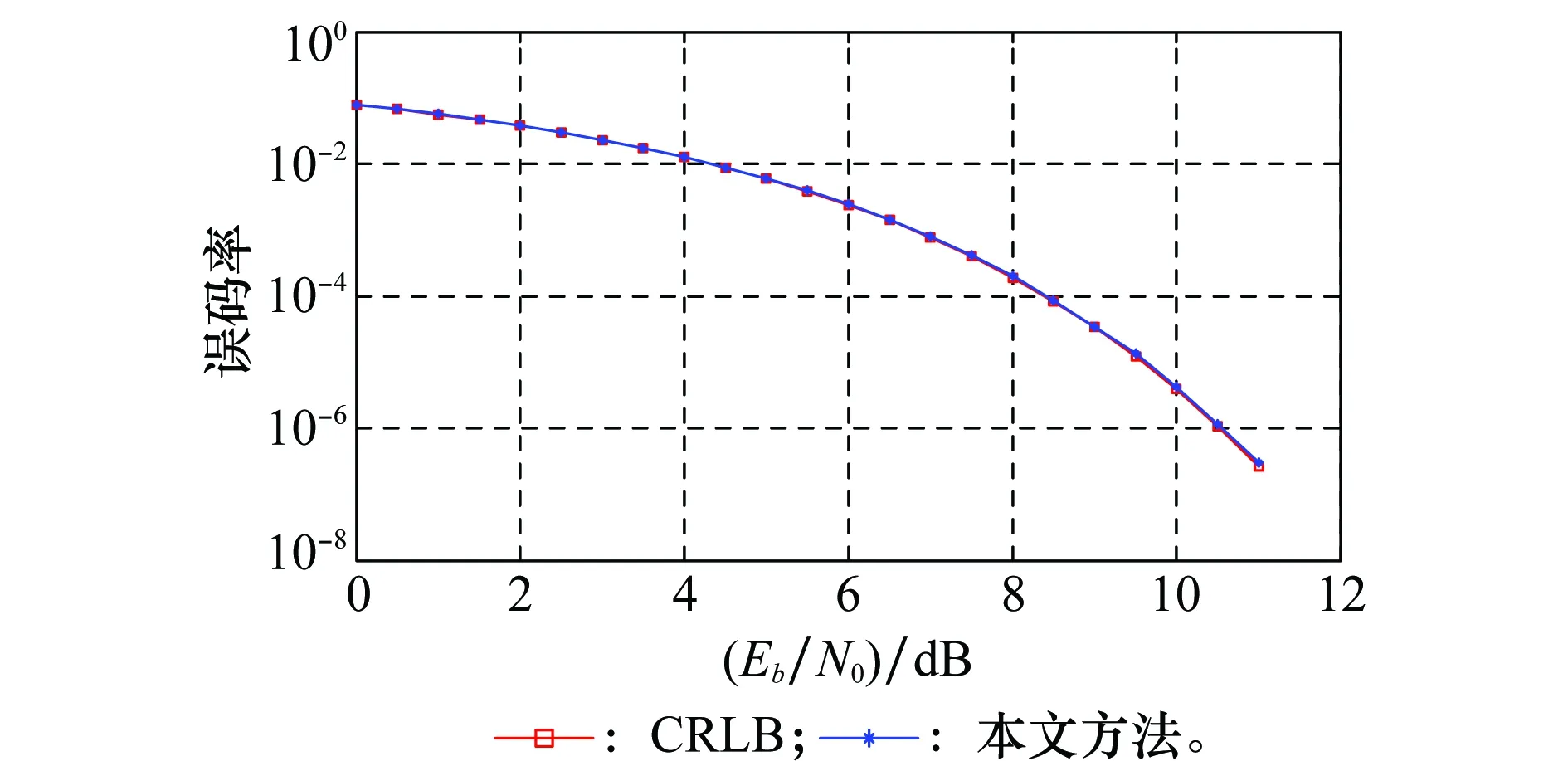
图10 本文方法误码率Fig.10 Error rate of the proposed method

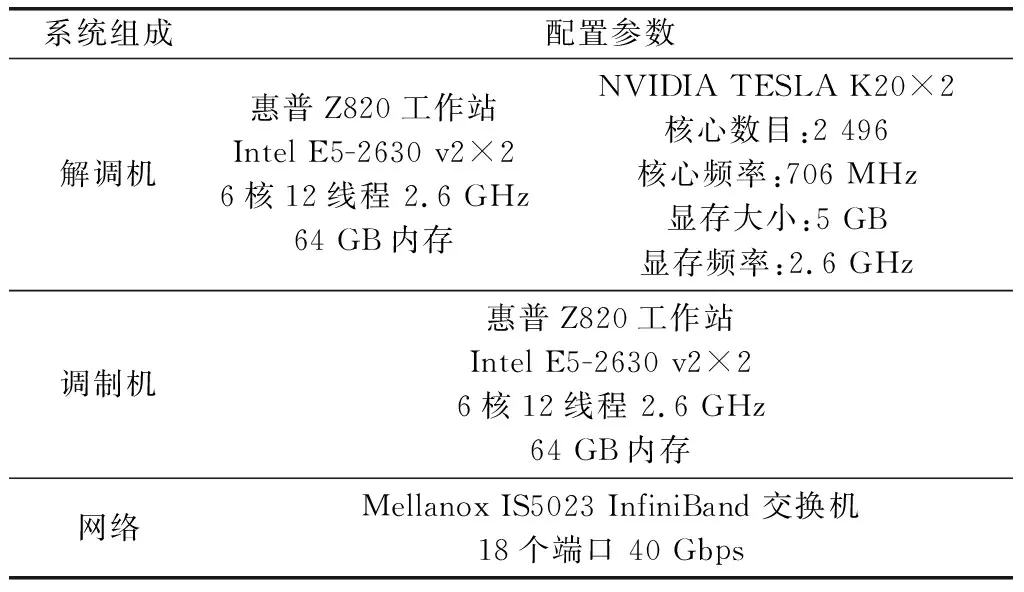
系统组成配置参数解调机惠普Z820工作站Intel E5-2630 v2×26核12线程 2.6 GHz64 GB内存NVIDIA TESLA K20×2核心数目:2 496核心频率:706 MHz显存大小:5 GB显存频率:2.6 GHz调制机惠普Z820工作站Intel E5-2630 v2×26核12线程 2.6 GHz64 GB内存网络Mellanox IS5023 InfiniBand 交换机18个端口 40 Gbps

图11 系统硬件组成Fig.11 Hardware composition of the system

为了验证解调速度与解调进程数目的关系,采用以下3种测试方案:

方案1解调机使用5个解调进程+1块NVIDIA TESLA K20;

方案2解调机使用10个解调进程+1块NVIDIA TESLA K20;

方案3解调机使用15个解调进程+2块NVIDIA TESLA K20。

统计100 s稳定运行时间内信号解调机的网络接收速度,如图12所示。方案1的平均处理速度是826.9 MB/s,处理速度标准差是19.6 MB/s;方案2的平均处理速度是1 564.6 MB/s,处理速度标准差是17.5 MB/s;方案3的平均处理速度是2 308.3 MB/s,处理速度标准差是21.3 MB/s。

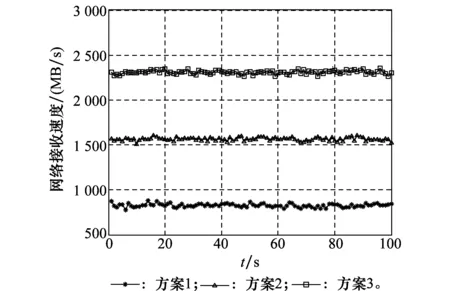
图12 信号解调机的网络接收速度Fig.12 Network receiving speed of the signal demodulator

经过分析,可以得到以下结论:处理速度与解调进程数近似成正比关系,增加计算资源可以有效提高处理速度。法国IN-SNEC公司的Cortex HDR 3200代表当前国际高码率接收机方面的最高发展水平,其QPSK解调速率高达3.2 Gbps。方案3的处理速度转化为信息速率后,为1 154.2 Mbps,虽然不及Cortex HDR 3200,但只要增加计算资源和解调进程数,就能实现解调速率的可持续提高。

6 结 论

本文提出一种适用于通用处理器平台的高速QPSK并行解调方法。该方法基于数据并行思想,将串行信号流拆分为信号块,能够充分利用多核多线程资源对各信号块进行处理,而后将各信号块处理结果进行综合,得到最终解调结果。此外,提出了一种适用于本并行解调方法的开环解调算法和相位模糊一致性方法。该解调算法基于ML,采用三维迭代搜索的方式,仿真结果表明,解调损失在0.1 dB以内。为了进一步将本文方法应用于通用处理器平台,在惠普Z820工作站上搭建调制解调验证系统。测试结果表明,处理速度与解调进程数近似成正比关系,增加计算资源可以有效提高处理速度。在2个NVIDIA TESLA K20+2个Intel E5-2630 v2的硬件配置下,每个符号4个采样点的采样条件下,得到了1 154.2 Mbps的码速率解调速度。

参考文献：

[1] STACKLER M, GLASCOTT A, CHANTIER N. A high speed transmission system using QAM and direct conversion with high bandwidth converters[C]∥Proc.of the Aerospace Conference, 2015: 1-8.

[2] RAVISHANKAR C, CORRIGAN J, GOPAL R. High data rate and bandwidth efficient designs for satellite communication systems[C]∥Proc.of the 35th IEEE International Communications Satellite Systems Conference, 2017: 5417-5420.

[3] YEM V V. Results on design and implementation of earth station based on software defined radio for geostationary satellite communication systems[J]. Systematic Biology, 2016, 55(1): 122-137.

[4] THUNE N N, HARIDAS S L. 4D-8PSK trellis coded modulation for high speed satellite communication[C]∥Proc.of the IEEE International Conference on Advances in Electronics, Communication and Computer Technology, 2017: 469-473.

[5] JIA Q, WANG X. Research on high-speed communication technology between DSP and FPGA[C]∥Proc.of the IEEE International Conference on Control and System Graduate Research Colloquium, 2017: 62-66.

[6] 林长星. 2Gbps高速通信解调技术及其实现研究[D]. 北京: 清华大学, 2012: 23-26.

LIN C X. Research on demodulation technique and its implementation for 2Gbps high speed communication[D]. Beijing: Tsinghua University, 2012: 23-26.

[7] 梁侠, 任海根, 徐先超,等. 800 Mb/s高速解调器的定时恢复算法及实现研究[J]. 现代电子技术, 2007, 30(23): 1-3.

LIANG X, REN H G, XÜ X C, et al. 800 Mb/s timing recovery algorithm and implementation for high speed demodulator[J]. Modern Electronics Technique, 2007, 30(23): 1-3.

[8] 郭晓峰, 郑雪峰, 卢满宏,等. 高速数传QAM解调器设计及应用[J]. 遥测遥控, 2011, 32(3): 21-25.

GUO X F, ZHENG X F, LU M H, et al. Design and application of high-data-rate QAM demodulator[J]. Journal of Telemetry, Tracking and Command, 2011, 32(3): 21-25.

[9] RHO S, PARK G, KIM J S, et al. A study on optimal scheduling using high-bandwidth memory of knights landing processor[C]∥Proc.of the 2nd IEEE International Workshops on Foundations and Applications of Self Systems, 2017: 289-294.

[10] KIRK R O, MUDALIGE G R, REGULY I Z, et al. Achieving performance portability for a heat conduction solver mini-application on modern multi-core systems[C]∥Proc.of the IEEE International Conference on Cluster Computing, 2017: 834-841.

[11] KIM J, KANG M, ISLAM M S, et al. A fast and energy-efficient Hamming decoder for software-defined radio using graphics processing units[J].The Journal of Supercomputing,2015,71(7):2454-2472.

[12] WUBBEN D, ROST P, BARTELT J S, et al. Benefits and impact of cloud computing on 5G signal processing: flexible centralization through cloud-RAN[J]. IEEE Signal Processing Magazine, 2014, 31(6): 35-44.

[13] YUAN Z, WANG J, JIANG K, et al. A real-time ISAR imaging structure based on GPU and CPU heterogeneous parallel processing[C]∥Proc.of the 13th IEEE International Conference on Signal Processing, 2016: 1539-1544.

[14] TRUONG N B, SUH Y J, YU C. Latency analysis in GNU radio/USRP-based software radio platforms[C]∥Proc.of the IEEE Military Communications Conference, 2014: 305-310.

[15] ANJANA C, SUNDARESAN S, ZACHARIA T, et al. An experimental study on channel estimation and synchronization to reduce error rate in OFDM using GNU radio[J]. Procedia Computer Science, 2015, 46: 1056-1063.

[16] LI R, DOU Y, ZHOU J, et al. CuSora: real-time software radio using multi-core graphics processing unit[J]. Journal of Systems Architecture, 2014, 60(3): 280-292.

[17] ALMRADI A, HAMDI K A. DA and NDA SINR estimation in non Gaussian noise[C]∥Proc.of the IEEE International Conference on Wireless Communications and Networking, 2015: 642-646.

[18] LI M, ZHAO J, CHEN L. Multi-symbol QPSK partitioning for improved frequency offset estimation of 16-QAM signals[J]. IEEE Photonics Technology Letters, 2015, 27(1): 18-21.

[19] OYAMA T, HOSHIDA T, NAKASHIMA H, et al. Linewidth-tolerant carrier phase estimation for N-PSK based on pilot-assisted N/2th-power method[C]∥Proc.of the 42th European Conference on Optical Communication, 2016: 19-21.

[20] FIALA P, LINHART R. Symbol synchronization for SDR using a polyphase filterbank based on an FPGA[J]. Radio Engineering, 2015, 24(3): 772-782.