基于固定时间一致性的无人机集群构型变换

梁晓龙, 刘 流, 何吕龙, 史振庆, 任宝祥

(空军工程大学空管领航学院, 陕西 西安 710051)

0 引 言

近年来,无人机(unmanned aerial vehicle,UAV)集群的编队控制问题得到了来自科研和工程领域的关注,并取得了大量研究成果[1-2]。在军事应用中如集群无源定位协调构型[3]、集群协同反隐身构型[4]等便是通过形成特定的编队构型使集群具有不同的功能。在具体任务执行过程中,集群往往需要根据不同要求在不同构型间进行变换。此时能够准确掌握集群构型变换所需时间,使得集群在指定时间内完成构型变换对于任务行动的规划与执行具有重要意义[5]。

在集群系统的构型变换与重构的研究方面,国内外学者已经取得了一些成果。文献[6]提出了一种基于多智能体的混合优化算法,在重构的不同阶段采取不同的策略:采用变分法来产生燃料最优的重构路径,并利用动态规划方法来进行全局的任务分配,利用遗传算法来决定重构编队构型,但该算法并未考虑在重构过程中的防撞问题。文献[7]在此基础上提出了分层进化路径规划方法,实现了重构过程中集群间的防撞,并采用了最优控制的思想解决重构问题。文献[8]则将集群构型的重构定义为参数的最优化问题,提出了混合粒子群遗传算法,提高了寻找全局最优解的收敛速度,实现了时间和燃料最优的集群重构。

随着一致性理论的发展[9],多智能体信息一致性理论也逐渐应用于集群系统的编队控制、群集运动和状态估计等领域,仅依靠局部信息交互的一致性算法日渐成熟[10]。文献[11]研究了具有时延的二阶多智能体系统编队控制问题,设计了基于位置和速度信息的编队控制协议并给出了协议中增益矩阵的确定方法。文献[12]进一步研究了具有切换拓扑的二阶多智能体系统的编队控制问题,给出了实现时变编队的充要条件,讨论编队可实现的约束条件,并利用多架四旋翼无人机对理论分析结果进行了实验验证。但以上文献关于多智能体系统一致性问题的研究都是渐进一致结果,无法使系统在指定时间内达到一致。文献[13]提出了多智能体系统基于连续状态反馈的分布式有限时间一致性协议,开始关注一致性中的收敛速率问题。文献[14]针对有领导者和无领导者的多智能体系统,通过“加幂积分器”的方法提出了连续的有限时间一致性协议,但该方法能否使得系统在有限时间达到一致还取决于智能体的初始状态。文献[15-18]提出了具有时延、非线性扰动情况下多智能体系统的固定时间一致性协议,且与智能体的初始状态无关,实现了固定时间内的一致,但系统无法按照期望构型收敛。

本文在固定时间一致性理论研究成果基础上,重点解决具有一阶积分特性的无人机集群系统在固定时间内实现期望构型变换的问题,创新点主要有两点:一是通过在现有固定时间一致性协议中引入编队参考向量,实现了无人机集群能够完成指定的构型变换;二是搭建四旋翼无人机集群系统,利用系统对所设计的控制协议进行飞行实验,验证了理论结果的有效性。

符号说明:本文中,在不引起歧义的情况下,用1(0)表示元素全为1(0)的相应维数的矩阵或向量,sig(x)α=sign(x)|x|α,在仿真及实验过程中涉及到的位置单位为米(m),速度单位为米每秒(m/s)。

1 预备知识

将每个智能体作为节点,则智能体网络拓扑通常用有向图G=(W,E,A)来描述,其中W=(w1,w2,…,wn)为非空有限的节点集合,E={(wi,wj):wi,wj∈W(G)}为边集,A=[aij]∈RN×N为非负邻接矩阵。在图G中,若节点i与节点j之间存在信息交换,则存在边(wi,wj);若信息交换是没有方向性的,即(wi,wj)∈E⟺(wj,wi)∈E,则称图G为无向图;若信息流只从节点j流向节点i,即边是有方向性的,则称图G为有向图,可以将无向图看作有向图的特殊情况。如果在任意两个节点之间都存在至少一条路径,则图G为连通的。记节点i的邻居节点为集合Ni⊆W(G),即Ni={wj∈W:(wi,wj)∈E}。如果wj∈Ni(i≠j),则aij>0,否则aij=0。图的Laplacian矩阵L=[lij]∈RN×N定义为

(1)

为便于后文进一步研究,还需要以下引理。

引理1[19]对于无向图G,其邻接矩阵A和Laplacian矩阵L都是对称矩阵。如果G是连通的,则0是L的单一特征值,其余特征值均为正。

引理2[20]对于具有n个节点的连通无向图G,其Laplacian矩阵L具有以下性质:

(1) 对于任意

(2)L是半正定矩阵;

(3) 将L的特征值记为{0,λ2,λ3,…,λn}且满足0≤λ2≤λ3≤…≤λn,则第二小的特征值λ2>0,若1Tx=0,则xTLx≥λ2xTx。

引理3[15]如果存在一个连续径向有界函数V:Rn→R+∪{0}满足:

(1)V(x)=0⟺x=0;

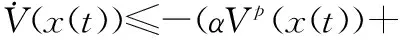
(2)

注1从引理3可以看出达到一致的时间T满足T≤Tmax。Tmax的取值只与α,β,p,q,k的取值有关,这些参数的取值只取决于一致性控制协议、智能体的数量以及Laplacian矩阵L第二小的特征值,与多智能体系统的初始状态无关。

引理4[21]取a1,a2,…,aN≥0,则

(3)

2 问题描述及固定时间一致性协议

2.1 问题描述

考虑由N个无人机组成的集群系统,多无人机之间的通信拓扑用无向图G描述,本文在固定连通拓扑下进行研究。无人机i∈{1,2,…,N}看作是G的节点wi。把单个无人机视为质点,其动力学模型采用一阶积分模型[16]:

(4)

其中,i=1,2,…,N,xi(t)、ui(t)分别表示第i个无人机的位置和速度,同时ui(t)也为对应的控制输入。假定无人机三维运动相互解耦,为便于描述,本文在一维的情况下进行分析,但所得的结论仍适用于二维平面及三维空间。

定义1∀i,j=1,2,…,N,如果存在固定时间T使得系统在任意初始状态下都满足:

(5)

则称系统能够在固定时间T内实现一致,并达到期望构型。

其中,rij=ri-rj为编队参考构型向量,R=[rij]为参考构型矩阵,固定时间T≤Tmax。

2.2 固定时间一致性协议

为实现无人机集群系统的固定时间一致性,设计如下基于位置信息的分布式控制协议:

(6)

式中,c1,c2,c3为正常数；p∈(0,1),q∈(1,∞)。协议式(6)在文献[16]的基础上引入了参考构型向量rij,从而使得集群编队能够按照期望构型达到一致。

为便于下文相关定理的证明,令ei=xi-ri,将协议(6)转化为如下形式:

(7)

注2从控制协议式(7)中可以看出,t时刻控制输入的产生是由无人机根据自身及邻居无人机的位置信息、与期望构型的对比所计算产生的,若输入产生频率在PIX自驾仪可执行的性能范围内,便可使集群达到期望位置,完成构型变换。

定理1无人机集群系统式(4)能够通过协议式(6)实现固定时间一致性的充分条件是:系统的无向通信拓扑图保持连通,即系统的Laplacian矩阵L≥0。

固定一致时间T满足:

(8)

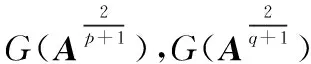
证明构造如下Lyapunov函数

(9)

则

(10)

由于

则

(11)

此时只需要L≥0,即矩阵L半正定,无向通信拓扑图连通即可满足

固定一致时间T满足式(8),定理1得证。

证毕

注3从定理1的证明可以看出,在理论上系统实现一致性的时间可以根据参数的设置任意指定,但在实际应用中,受到硬件性能的限制,往往需要根据实际情况具体考虑,选择合适参数实现指定时间内的一致性。

3 仿真及实验结果分析

本部分首先对所搭建的四旋翼无人机实验系统进行介绍,随后在Matlab环境下进行数值仿真并利用四旋翼无人机平台进行飞行验证,并对实验数据进行分析。

3.1 实验系统介绍

实验验证系统由四旋翼无人机平台、地面站、数据链共同组成,系统实物图如图1所示。

图1 四旋翼无人机实验系统Fig.1 Quadrotor experimental system

四旋翼无人机的飞行控制系统采用的是PIX自驾仪,自驾仪内置3组加速度计、3组陀螺仪、2组电子罗盘来估计四旋翼无人机的运动状态,并通过一张存储容量为4 GB的反式(trans flash,TF)存储卡记录实验数据。系统采用全球定位系统(global position system,GPS)作为定位模块为无人机提供实时定位导航,其频率为10 Hz,定位模块通过串口通信与无人机进行数据传输。实验系统为了实现无人机集群的分布式组网通信,采用基于Mesh组网技术的YL-800N自组网模块,通信频率为433 MHz。由于无人机在调用相关控制协议进行运动控制时需要一定的计算量和较高实时性,系统选用STM32F4系列微处理器进行实时运算。系统的硬件结构图如图2所示。

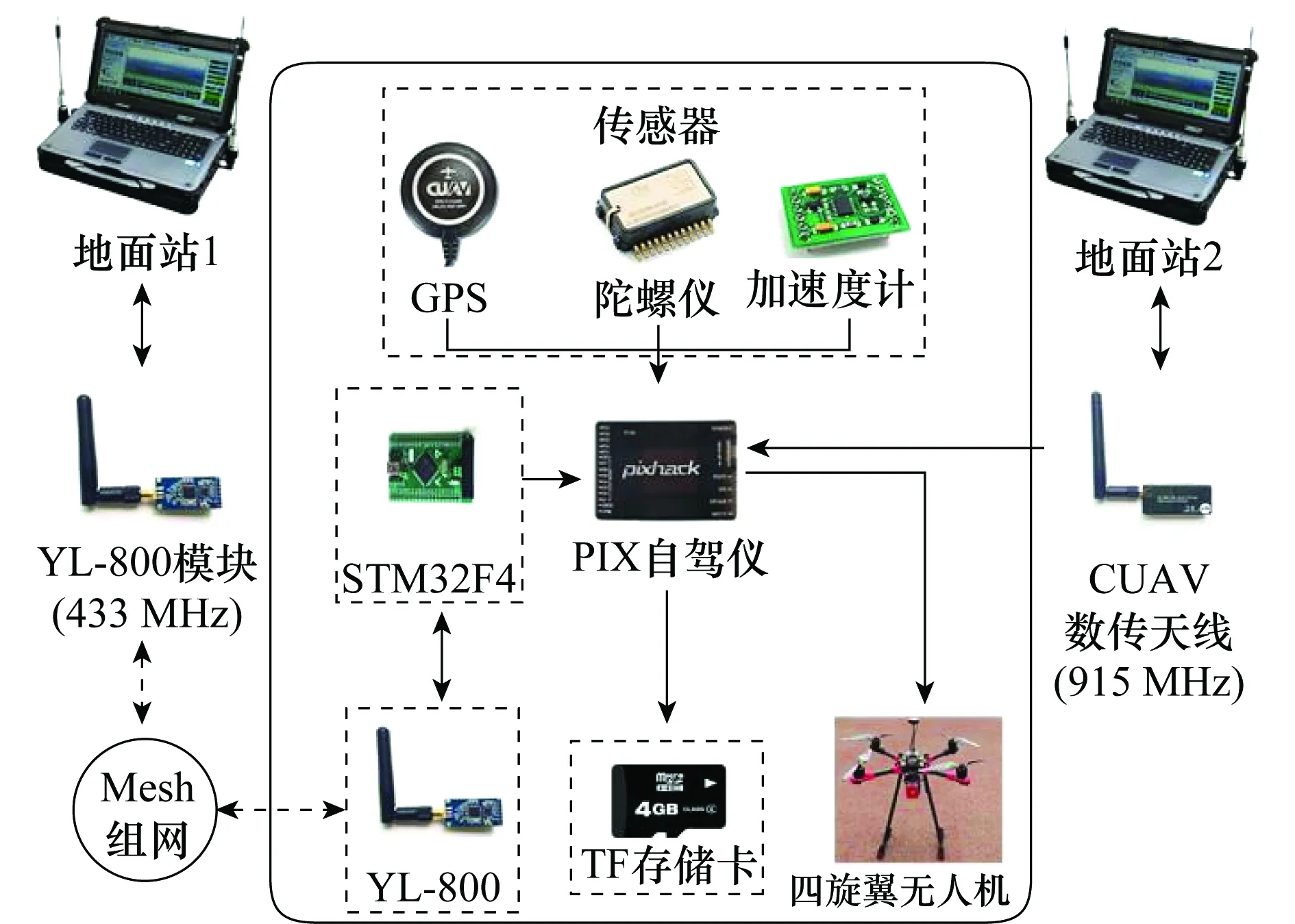
图2 实验系统硬件结构图Fig.2 Hardware structure of the experimental system

3.2 仿真及实验数据分析

考虑一个包含4架无人机的集群系统,在二维平面内进行运动并进行队形变换,相关系统矩阵为

式中,xix，xiy分别表示第i(i=1,2,3,4)架无人机的北向位置和东向位置。

无人机的初始状态为

相关参数为p=0.8,q=20,c1=0.5,c2=0.5,c3=5。为使无人机的速度符合无人机性能要求,对无人机速度输入大小作如下限制:

此时根据式(8)可以计算出固定一致时间T=47.49 s。

系统仿真流程如图3所示。首先根据构型变换的时间需求选择合适的控制协议参数,由于是分布式控制协议,各无人机根据控制协议以及邻居无人机的位置信息计算出自身的控制量,若控制量大小符合最大输入限制,则无人机按照控制量进行运动,否则经处理后由无人机执行,最终无人机集群在固定时间内达到期望构型。

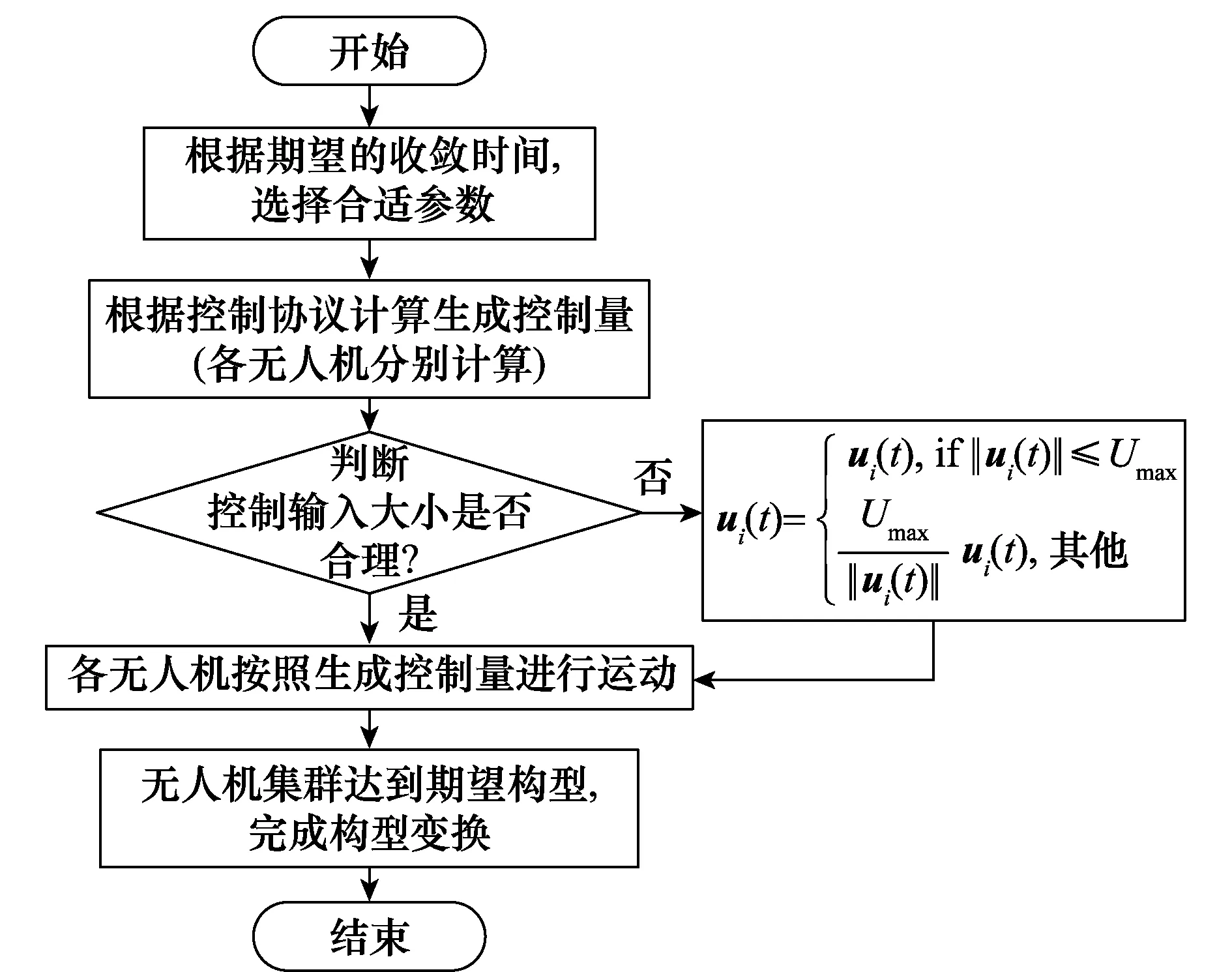
图3 仿真流程图Fig.3 Simulation flow chart

从编队控制协议式(6)中可以看出,每一架无人机只需要根据自身及与其通信的邻居无人机的位置信息和参考构型位置便可完成运动控制,无人机之间通过YL-800模块以10 Hz的频率进行组网通信。在本次实验验证中,位置信息由GPS定位模块进行测量(见图4～图7)。

在实验过程中,为避免无人机出现相撞,本文主要从两个方面进行设计考虑,首先将4架无人机的实验高度分别定为5 m、7 m、9 m、11 m,4架无人机分别在各自高度进行二维平面内的运动;其次在无人机中加入危险接近处置原则,即无人机在飞行过程中若感知到存在另外无人机与自身距离小于1 m,则停止飞行。实验过程中的飞行情况如图8所示。

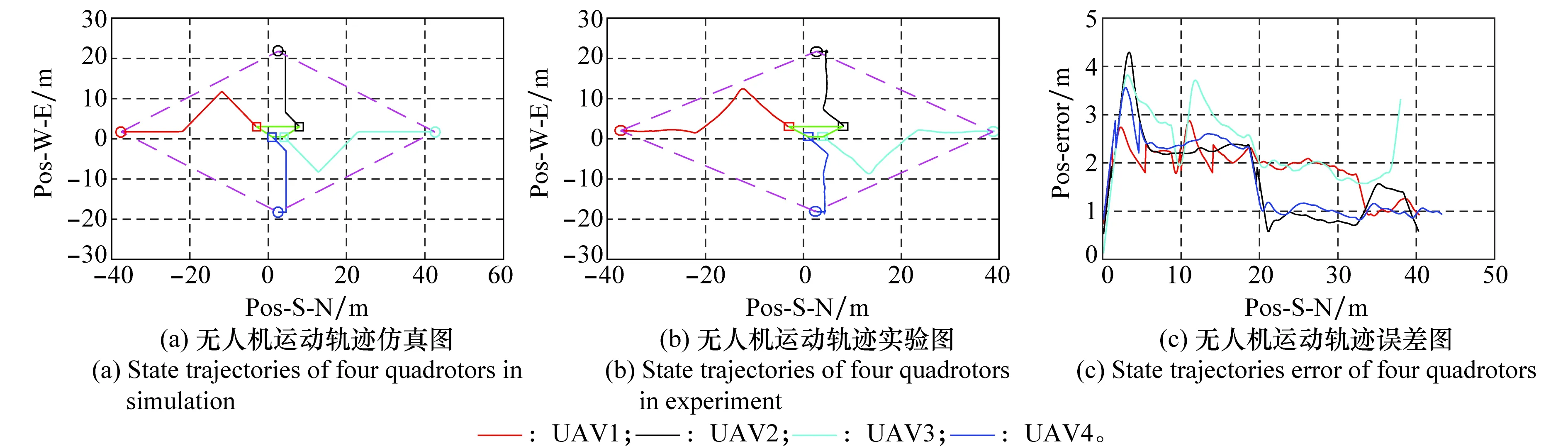
图4 运动轨迹图Fig.4 State trajectories of four quadrotors

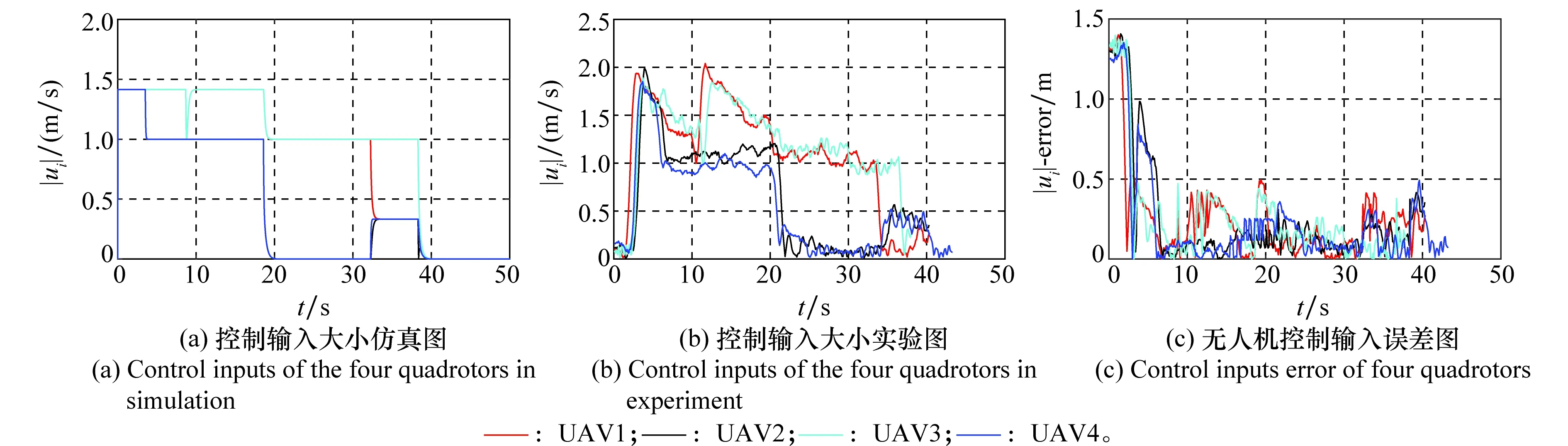
图5 控制输入变化图Fig.5 Control inputs of the four quadrotors

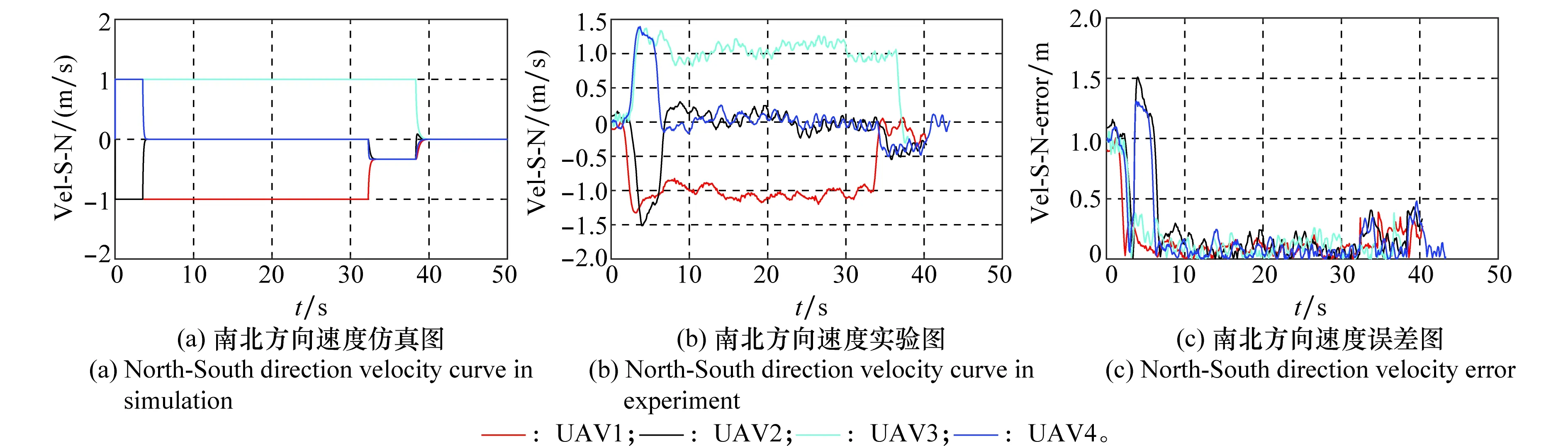
图6 南北方向速度变化图Fig.6 North-south direction velocity curve

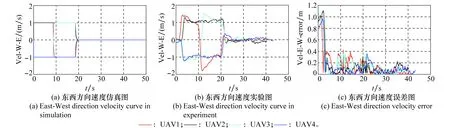
图7 东西方向速度变化图Fig.7 East-west direction velocity curve

图8 实验编队飞行图Fig.8 Formation flight image in experiment

无人机起飞后便由地面站向无人机发送指令,无人机进行组网通信,调用相应控制协议进行构型变换,从图4(b)中可以看出,无人机集群编队在固定通信拓扑的条件下,按照文中设计的编队控制协议,最终完成了期望构型的变换,其中,绿色实线为无人机初始构型,紫色虚线则表示最终期望构型,图4(c)反映了各无人机仿真运动轨迹与实验运动轨迹的误差变化图,从图中可以看出除少数时间误差达到3.5 m左右,其余时间均稳定在2 m左右,符合GPS实际定位误差,说明了实验结果的有效性。图5反映的是实验过程中控制输入大小的变化,从图5(b)中可以看出控制输入大小在40 s左右基本稳定在0,即无人机已经达到期望构型,且所用时间小于指定时间47.49 s,符合理论预期。图6、图7分别反映无人机在南北及东西方向上的速度大小变化。图5(c)、图6(c)以及图7(c)表现的是相关数据的仿真与实验数据误差变化图,从中可以看出实验数据仍存在一定的误差,主要是由传感器误差、通信时延以及外部环境因素造成的,除开始阶段外速度以及控制输入误差大小不超过0.5,实验结果依然具有有效性。

4 结 论

本文针对具有固定连通拓扑的一阶无人机集群,设计了固定时间一致性控制协议,确保集群系统能够在固定时间内实现一致。

(1) 通过引入参考编队构型向量,使得无人机集群能够完成期望构型的变换,其充分条件为通信拓扑保持连通,利用Lyapunov函数给出了相应证明；

(2) 搭建四旋翼无人机实验系统,利用4架四旋翼无人机对本文提出的控制协议进行实验验证,实验结果证明了本文方法的有效性。

参考文献：

[1] 梁晓龙,孙强,尹忠海,等.大规模无人系统集群智能控制方法综述[J].计算机应用研究,2015,32(1):11-16.

LIANG X L, SUN Q, YIN Z H, et al. Review on large-scale unmanned system swarm intelligence control method[J]. Application Research of Computers, 2015, 32(1): 11-16.

[2] LIANG X L, SUN Q, YIN Z H, et al. A study of aviation swarm convoy and transportation mission[C]∥Proc.of the 4th International Conference on Swarm Intelligence,2013:368-375.

[3] 胡利平,梁晓龙,张佳强.航空集群定位编队协调构型控制研究[J].计算机仿真,2016,33(9):45-49.

HU L P, LIANG X L, ZHANG J Q. Research on coordination formation configuration control of aircraft swarms location[J]. Computer Simulation, 2016, 33(9): 45-49.

[4] 张佳强,梁晓龙,尹忠海,等.航空集群协同反隐身构型与机动策略[J].系统工程与电子技术,2016,38(11): 2518-2522.

ZHANG J Q, LIANG X L, YIN Z H, et al. Design of aircraft swarm cooperating anti-stealth configuration and maneuver strategy[J].Systems Engineering and Electronics,2016,38(11):2518-2522.

[5] 沈林成, 王祥科, 朱华勇, 等. 基于拟态物理法的无人机集群与重构控制[J]. 中国科学: 科学技术, 2017, 47(3): 266-285.

SHEN L C, WANG X K, ZHU H Y, et al. UAVs flocking and reconfiguration control based on artificial physics[J]. Scientia Sinica Technologica, 2017, 47(3): 266-285.

[6] YANG G, YANG Q S. Fuel optimal manoeuvres for multiple spacecraft formation reconfiguration using multi-agent optimization[J]. International Journal of Robust and Nonlinear Control, 2002, 12: 243-283.

[7] WANG S Y, ZHENG C W. A hierarchical evolutionary trajectory planner for spacecraft formation reconfiguration[J]. IEEE Trans.on Aerospace and Electronic System,2012,48(1):279-289.

[8] DUAN H B, LUO Q N, SHI Y H. Hybrid particle swarm optimization and genetic algorithm for multi-UAV formation reconfiguration[J].IEEE Computational Intelligence Magazine,2013,8(3): 16-27.

[9] SABOORI I, KHORASANI K.H∞Consensus achievement of multi-agent systems with directed and switching topology networks[J]. IEEE Trans. on Automatic Control, 2012, 59(11): 3104-3109.

[10] LUO X Y, HAN N N, GUAN X P. Leader-following consensus protocols for formation control of multi-agent network[J]. Journal of Systems Engineering and Electronics, 2011, 22(6): 991-997.

[11] HAN L, DONG X W, LI Q D, et al. Formation tracking control for time-delayed multi-agent systems with second-order dynamics[J].Chinese Journal of Aeronautics,2016,30(1):348-357.

[12] DONG X W, ZHOU Y, REN Z, et al. Time-varying formation tracking for second-order multi-agent systems subjected to switching topologies with application to quadrotor formation flying[J]. IEEE Trans.on Industrial Electronics,2017,64(6):5014-5024.

[13] WANG L, FENG X. Finite-time consensus problems for networks of dynamic agents[J]. IEEE Trans. on Automatic Control, 2010, 55(4): 950-955.

[14] LI S, DU H, LIN X. Finite-time consensus algorithm for multi-agent systems with double-integrator dynamics[J]. Automatica, 2011, 47(8): 1706-1712.

[15] POLYAKOV A. Nonlinear feedback design for fixed-time stabilization of linear control systems[J]. IEEE Trans. on Automatic Control, 2012, 57(8): 2106-2110.

[16] ZHANG B, JIA Y. Fixed-time consensus protocols for multi-agent systems with linear and nonlinear state measurements[J]. Nonlinear Dynamics, 2015, 82(4): 1683-1690.

[17] DEFOORT M, POLYAKOV A, DEMESURE G, et al. Leader-follower fixed-time consensus for multi-agent systems with unknown nonlinear inherent dynamics[J]. IET Control Theory Application, 2015, 9(14): 2165-2170.

[18] WANG Q, WANG Y, SUN C. Fixed-time consensus of multi-agent systems with directed and intermittent communications[J]. Asian Journal of Control, 2016, 19(1): 1-11.

[19] GODSIL C, ROYLE G. Algebraic graph theory[M]. New York: Springer-Verlag, 2001.

[20] OLFATI-SABER L, MURRAY R M. Consensus problems in networks of agents with switching topology and time-delays[J].IEEE Trans.on Automatic Control,2004,49(9):1520-1533.

[21] ZUO Z, LIN T. Distributed robust finite-time nonlinear consensus protocols for multi-agent systems[J]. International Journal of Systems Science, 2014, 47(6): 1-10.