α稳定分布噪声下水声线性调频信号的识别

孟庆松, 王 彬, 邵高平

(信息工程大学信息工程学院,河南 郑州 450001)

0 引 言

线性调频(linear frequency modulation,LFM)信号具有较好的自相关特性和较宽的多普勒容限,在水下经常被用作水声通信同步信标、鱼雷或主动声纳的探测信号。在水声侦察和对抗过程中,识别出接收信号为LFM信号,有助于水声通信信号的捕获、信息恢复和水下目标探测。

目前,对水声LFM信号的识别方法多是假设在加性高斯白噪声(additive Gaussian white noise, AGWN)环境下,比如基于魏格纳分布的方法[1-2]、基于短时傅里叶变换(short-time Fourier transform,STFT)的方法[3-5]、基于自相关和循环谱[6-7]的方法及基于分数阶傅里叶变换(fractional Fourier transform,FRFT)[8-10]的方法。事实上,水声信号传播中受水声多途效应的影响,正确识别水声信号必须选择对水声多途效应稳健的信号特征,文献[11]讨论了存在水声多途信道和AGWN条件下的水声信号识别问题,提出了对水声多途效应稳健的水声LFM循环谱特征。然而,在浅海水声环境中,由于工业活动、地震风暴及海洋生物等因素的影响,会存在大量的脉冲干扰,这种噪声通常用α稳定分布来描述[12-15]。α稳定分布噪声具有明显的尖峰脉冲噪声特性,不存在有限的二阶及以上各阶统计量[16],使得上述算法的检测性能明显下降。

近年来,在α稳定分布噪声下对LFM信号的处理问题逐渐受到人们的关注[17-19],但公开研究成果并不多见,文献[17]利用了基于STFT的方法,通过设置损失函数对传统的STFT进行优化,并进行Radon变换,通过设定的阈值对LFM信号进行检测,但该方法在低信噪比(signal-to-noise ratio，SNR)条件下性能严重下降,且文中并未考虑信道条件。2016-2017年,文献[18-19]在进行α稳定分布噪声下的LFM信号参数估计时使用了基于稳健S变换和最优L-柯西加权的方法,取得了一定的改进效果。

为了提高浅海水声环境下LFM信号的识别性能,提出了基于非线性变换的离散分数阶傅里叶变换(discrete fractional Fourier transform,DFRFT)方法,用以检测浅海水声LFM信号。该方法首先对接收信号进行非线性变换,然后进行DFRFT,构造出LFM信号识别特征量,最后利用支持向量机(support vector machine,SVM)作为分类器,对LFM信号进行识别。仿真实验结果表明,在混合信噪比(mixed signal-to-noise ratio,MSNR)为-15 dB时正确识别率高于94%。

1 信号模型

α稳定分布噪声下接收到的浅海水声信号模型为

y(t)=s(t)⊗h(t)+w(t)

(1)

式中,符号“⊗”表示卷积运算;y(t)为接收信号;s(t)为发送信号,其调制类型为集合{LFM,MPSK,MFSK,OFDM}的任意一种。如果发送信号为LFM信号,其表达式为

s(t)=Aexp(jπkt2+2jπf0t)

(2)

式中,A表示LFM信号幅度;k为LFM信号的调频斜率;f0是初始频率。

若发送信号为多相移键控(multiple phase shift keying，MPSK)信号,其表达式为

(3)

若发送信号为多频移键控(multiple frequency shift keying,MFSK)信号,其表达式为

(4)

式中,fΔ为频率偏移量;Δf=2fΔ为频率间隔;sl表示传输符号。

若发送信号为正交频分复用(orthogonal frequency division multiplexing,OFDM)信号,其表达式为

(5)

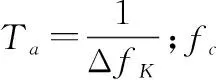
h(t)为水声多途信道的冲激响应,其表达式为

(6)

式中,N为多径数目,当i=0,τ0=0时为直达声道。τi(i≠0)为第i条声线相对于第0条声线的延时,Ai为第i条声线的幅度,fdi为第i条声线的多普勒频移。

w(t)为与发送信号s(t)相独立的噪声信号,服从α稳定分布。参数α为特征指数,0<α≤2,脉冲性随着α的增大而减小,当α=2时脉冲噪声退化为高斯噪声。图1为不同α值所对应的标准对称α稳定(symmetricαstable,SαS)分布噪声[16]的时域波形与时频图。

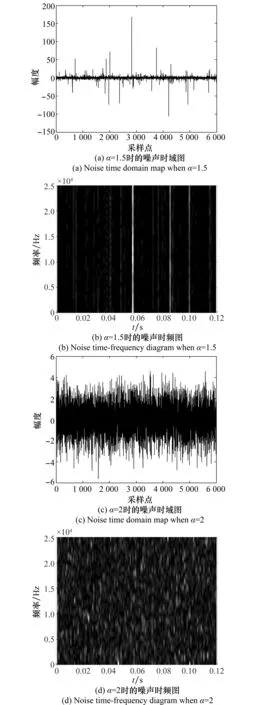
图1 不同α值的标准SαS分布噪声及时频图Fig.1 Standard SαS distributed noise and time-frequency diagram in different α

可以看出,随着特征指数的减小,脉冲数量增多、幅度增强。当α=2时,噪声变成平稳的高斯噪声。从时频图1可以看出,α稳定分布噪声与高斯白噪声(white Gaussian noise，WGN)具有明显的区别。α稳定分布噪声在时频域上会出现带状的频域很宽的能量分布,且在时域上分布不均匀,而WGN在时频域上的能量是均匀分布的。

2 基于非线性映射DFRFT的水声LFM信号识别方法

本文针对浅海水声多途脉冲噪声信道环境,以典型水声信号集{LFM,MPSK,MFSK,OFDM}为待识别信号集,研究LFM信号的识别问题,提出了基于非线性映射DFRFT的LFM信号识别算法,算法的处理框图如图2所示。

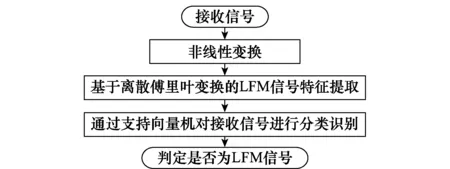
图2 基于非线性映射DFRFT的LFM信号识别算法流程Fig.2 LFM signal recognition algorithm process based on DFRFT ofnonlinear mapping

2.1 对接收信号进行非线性变换

α稳定分布噪声具有明显的尖峰脉冲特性,可利用非线性函数对接收信号进行非线性变换,对脉冲噪声进行抑制。首先对接收信号y(t)定义非线性变换[20]，即

(7)

将式(1)代入式(7),有

(8)

2.2 基于DFRFT的LFM信号特征提取

根据FRFT的定义式[21],对非线性变换后的接收信号进行FRFT,有

(9)

式中,P为阶数;K(t,u)为核函数,定义[16]为

KP(t,u)=

(10)

式中,n为整数;u为变换域;β表示旋转角度,β与P的关系为β=Pπ/2,将式(2)代入式(10)可得

(11)

从式(11)中可知,FRFT可以理解为旋转角度为β的时频面旋转,当阶数变化到一定范围时,LFM信号在对应阶次的FRFT域上具有集聚效应,出现较高的峰值,当阶数为最佳阶数时,k=-cotβ,此时变换域出现的峰值最大。因此,可利用基于FRFT的方法对LFM信号进行检测。

由式(2)和式(6)可得接收信号为

y(t)=w(t)+A0s(t)exp(j2πfd0t)+

(12)

根据FRFT的性质[22],有

FP[y(t)]=Np(u)+A0Fp[s(t)exp(j2πfd0t)]+

Np(u)+A0Sp(u-fd0sinβ)·

(13)

式中,FP[y(t)]是阶数为P时y(t)的FRFT结果;Np(u)为噪声部分的FRFT,若发送信号为LFM信号且Np(u)的影响较小时,从式中可知,当阶数为最佳阶数时,在FRFT域会形成一系列峰值。

由于工程计算中为离散形式,计算时需要使用DFRFT方法,这里采用基于分解型的DFRFT[21],即

(14)

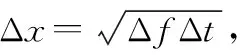
分别以步长ΔP和Δm对参数P和m进行遍历,其中ΔP=0.005,Δm=1得到接收信号的FRFT信息。

将非线性变换后的信号带入DFRFT式(14)中,可得

(15)

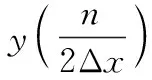
现有的基于FRFT对LFM信号检测的方法多通过使用阈值的方法来判定有无LFM信号[17],在低SNR和α稳定分布噪声下的检测性能不稳定,对阈值的依赖性较高。对此,本文提出了基于方差比的检测识别方法,可有效提高检测性能。

从式(13)可知,若发送信号为LFM信号且噪声分量在分数域的影响较小,当阶数为最佳阶数时,在FRFT域会形成一系列峰值;当阶数为1时,FRFT退化为普通的傅里叶变换,接收信号在频域表现为一个带宽较大的信号。因此可将两者的归一化方差比作为特征量进行LFM信号的识别。

(16)

(17)

式中,max(·)表示求最大值。

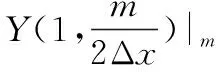
(18)

式中,max(·)表示求最大值。

通过分别计算这2种阶数时信号在FRFT域上的方差,得到方差的比值并作为特征量,即

(19)

(20)

识别特征量定义为

(21)

2.3 通过SVM对接收信号的特征量进行分类识别

SVM是一种有监督的机器学习算法,可用于分类问题。他使用一种称为核函数的技术找到2种分类之间的最佳边界[23]。

不同的海域和不同的SNR条件会对LFM信号的识别特征量产生一定影响。与通过阈值进行判决相比,使用SVM进行分类可在不同条件下均找到最佳分类边界,且可以通过不断增加训练信号改进最佳边界。近年来,也有人提出一些实用的方法对SVM的性能进行改进,如对数据处理方式进行调整,大样本类多取样,小样本类少取样等[24-26]。

通过Matlab仿真软件产生典型海洋水声信号声源波形数据。首先,产生不同调制方式的水声通信信号(比如调制方式为MPSK、MFSK、OFDM等)、不同参数的LFM信号、不同种类的舰船辐射噪声(比如不同螺旋桨数、不同螺旋桨叶片数的舰船)等。

根据全球海洋信息数据(比如Argo全球海洋信息数据集[27]),通过经验公式可以得到不同海域的声剖面信息,即

c=1 449.2+4.6T-0.055T2+

(1.34-0.010T)(S-35)+0.016z

(22)

式中,c为声速，m/s;T为温度，℃;S为盐度，‰;z为深度，m。

然后,利用Bellhop仿真软件,得到不同深度、不同传输距离条件下的声信道冲激响应。各种声源波形与不同信道的冲激响应卷积运算,然后再叠加上不同强度的噪声,得到接收传感器的接收波形,将此仿真信号波形作为SVM训练的样本数据。

其中,叠加的噪声为不同特征指数的α稳定分布噪声,用MSNR来刻画其噪声强度,即

(23)

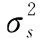
选用SVM为分类器,根据待检测信号所发生的海域,选取该海域或最临近海域的样本数据,计算识别特征量,并对SVM分类器进行训练。

然后,计算待测信号的识别特征量,并将其送入训练好的SVM分类器中进行LFM信号的识别,即可完成在浅海水声条件下对LFM信号的检测。

3 仿真实验及分析

为验证本文方法的有效性,设计仿真实验进行验证。仿真实验条件为:噪声为加性标准SαS 分布噪声,噪声特征指数为α=1.5。根据Argo全球海洋信息数据集,得到东海某海域的声剖面信息,如图3所示。

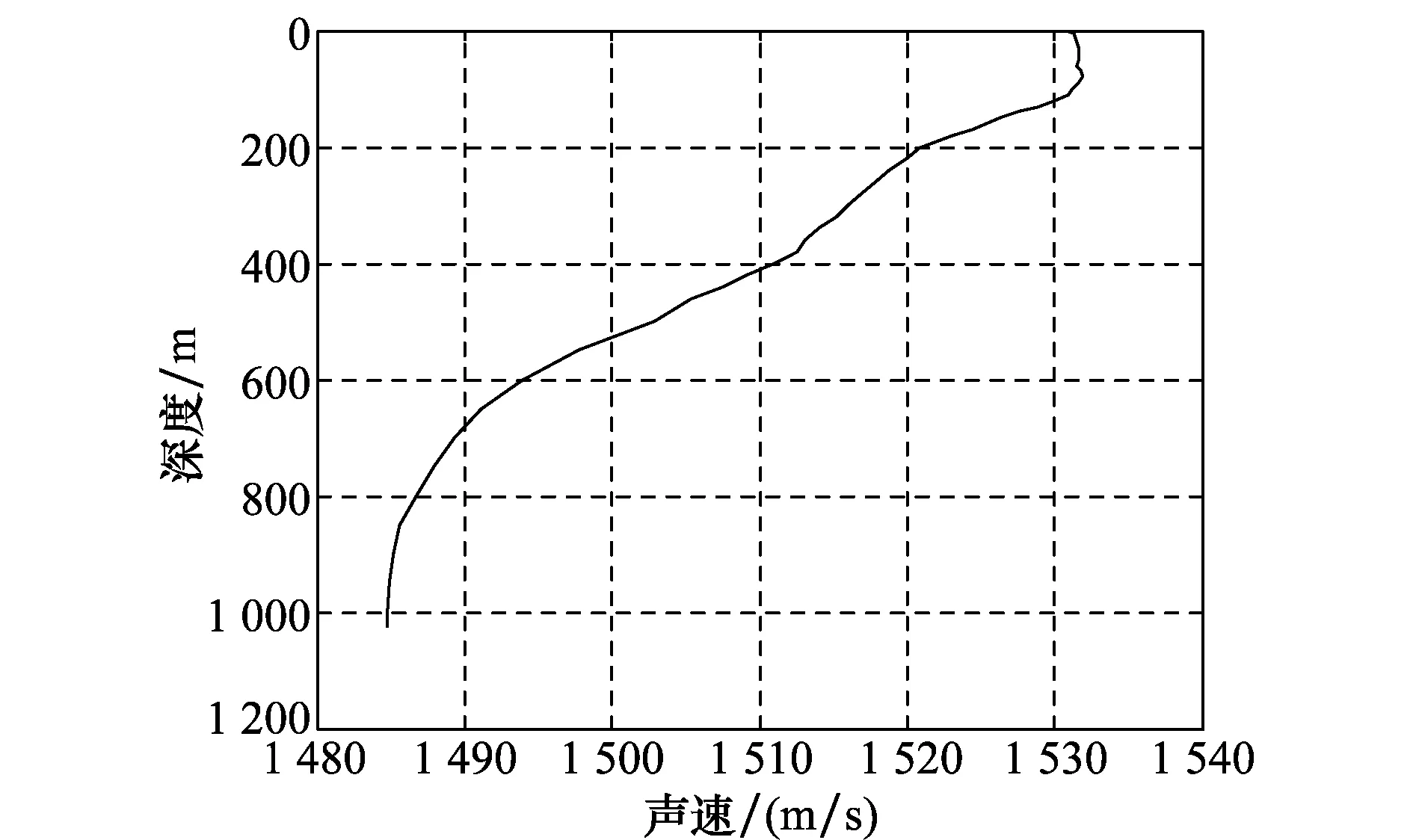
图3 东海某海域声剖面图Fig.3 Acoustic profile of sea area in the East China Sea

将发送端、接收端的深度分别设置为200 m、300 m,发送端、接收端的水平距离为2 000 m,通过Bellhop仿真得到传输信道的冲激响应,如图4所示。

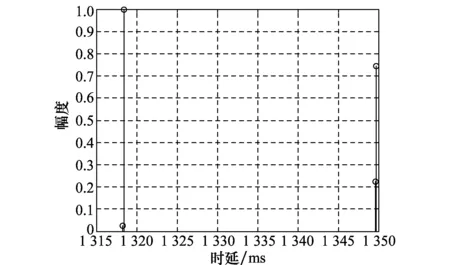
图4 东海某海域冲激响应图Fig.4 Impulse response diagram of sea area in the East China Sea

3.1 非线性变换改进性能分析

首先,验证α稳定分布噪声下非线性变换对LFM信号检测性能改进的有效性。仿真实验条件为:发送LFM信号的初始频率为13 kHz,带宽为5 kHz,采样频率50 kHz,采样时间为50 ms;信道采用上述Bellhop仿真得到的东海某海域信道;噪声为加性标准SαS分布噪声,噪声特征指数为α=1.5。图5(a)是LFM信号未经过非线性变换后的DFRFT(MSNR=-5 dB),图5(b)为LFM信号经过非线性变换后的DFRFT(MSNR=-5 dB),图5(c)是LFM信号未经过非线性变换后的DFRFT(MSNR=-15 dB),图5(d)是LFM信号经过非线性变换后的DFRFT(MSNR为-15 dB)。

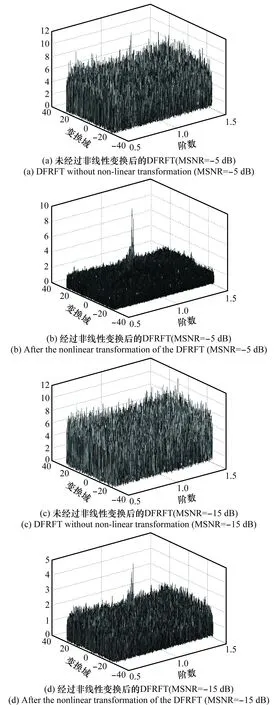
图5 非线性变换对DFRFT结果的影响Fig.5 Influence of nonlinear transformation on DFRFT results

对比图5可以看出,由于α稳定分布噪声的影响,传统的基于FRFT的方法性能严重下降,特征遭到严重破坏,而非线性变换可以很好地抑制α稳定分布噪声。

3.2 提取特征信息并通过SVM对接收信号的特征量进行分类识别

首先,在东海某海域仿真信道和稳定分布噪声条件下,MSNR在-15～10 dB范围内,选取12个不同参数的仿真信号,包括FSK、PSK、OFDM和LFM信号,其中LFM的信号初始频率为13 kHz,带宽为2 kHz、3 kHz、4 kHz、5 kHz、6 kHz、7 kHz,信号长度均为50 ms,每间隔5 dB对每种信号进行50次蒙特卡罗仿真实验,计算特征量归一化方差比的值并取平均,得到不同类型信号在不同MSNR条件下的方差比。

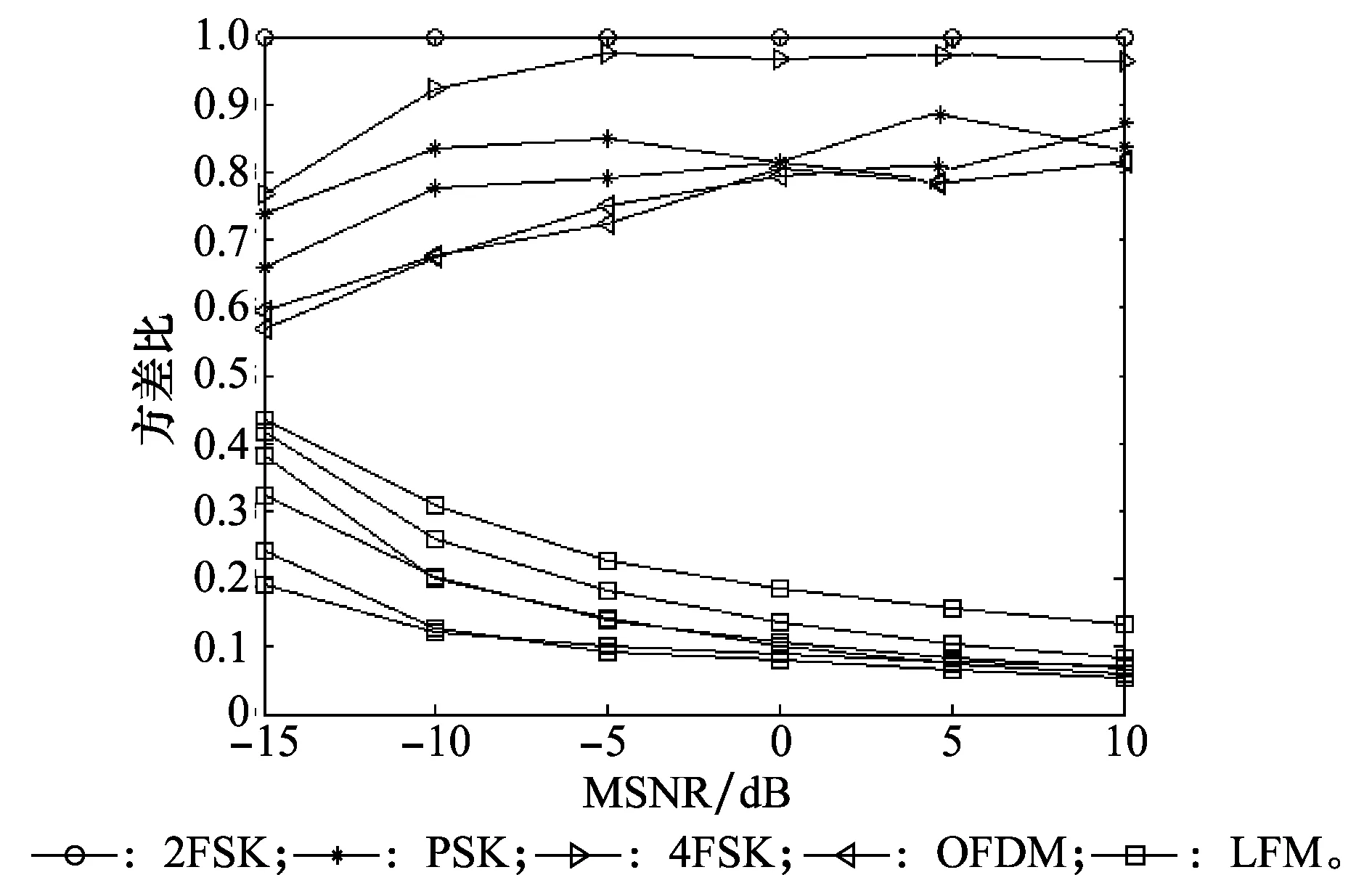
图6 不同类型信号在不同MSNR条件下的方差比Fig.6 Variance ratio of different types of signals under different MSNR corditions

从仿真数据可知,利用方差比作为特征量对LFM信号进行识别是可行的。

根据Argo全球海洋信息数据集,得到东海某海域和南海某海域的声剖面信息。通过Bellhop仿真得到相应的水声信号仿真波形。对仿真接收信号计算识别特征量,并对SVM分类器进行训练。

训练完成后,对LFM的识别率进行测试。在MSNR -15 ～10 dB范围内,每间隔1 dB产生500组随机的信号,包括PSK、FSK、OFDM及带宽为2～7 kHz的LFM信号。将仿真得到的信道冲激响应与信号卷积,并选择噪声条件为加性标准SαS分布噪声,特征指数为α=1.5,得到待测信号。

将待测信号送入训练好的SVM分类器中进行LFM信号的识别,得到LFM的识别率随MSNR变化的曲线。此外,将文献[17]所述的基于Robust STFT的方法在信号长度为50 ms情况下进行仿真,结果如图7(a)所示,仿真结果表明,本文提出的方法有了较大改进。选取南海某海域的仿真信道,在同样条件下得到如图7(b)所示的结果。

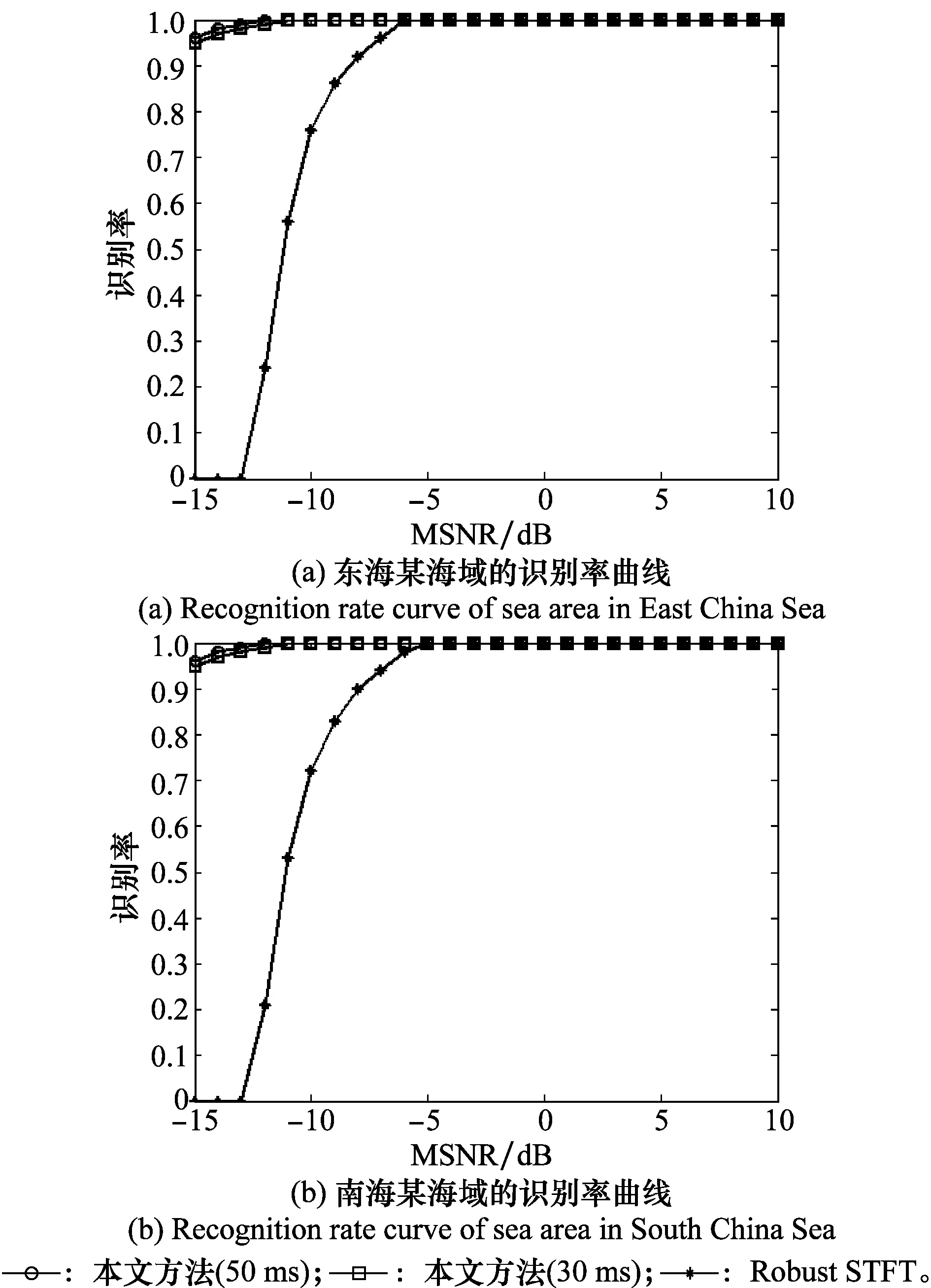
图7 在不同MSNR条件下对LFM信号的识别率曲线Fig.7 Recognition rate curve of LFM signal under different MSNR conditions

由图可知,与文献[17]所述方法相比,本文提出的方法有了较大改进。

为了验证在不同α值的稳定噪声条件下识别率的变化情况,选取了0.8、1.2、1.5、1.8、2作为α值进行仿真实验。实验采用上述东海某海域信道条件,对每个α值,MSNR在-15～10 dB范围内,每间隔1 dB产生100组随机的带宽为2～7 kHz的LFM信号进行仿真实验,结果如图8所示。

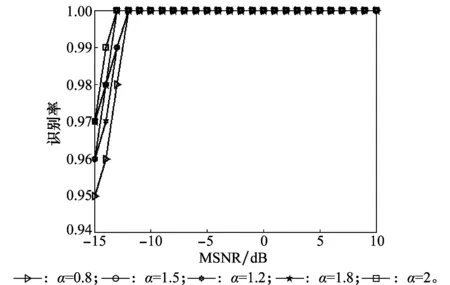
图8 在不同α值条件下对LFM信号的识别率曲线Fig.8 Recognition rate curve of LFM signal under different α

仿真实验说明,本文所述方法在不同的α值环境中性能较稳定,且均有较高的识别率。

4 结 论

本文提出了基于非线性映射DFRFT的LFM信号识别方法。首先,通过非线性变换对α稳定分布噪声进行抑制,然后进行FRFT并通过提取的归一化方差比特征量识别出LFM信号。仿真表明,该方法在MSNR和α稳定分布噪声条件下能够有效识别LFM信号。

参考文献：

[1] 梁国龙,生雪莉. 基于WVD-HT的宽带调频信号检测技术研究[J]. 电子学报, 2011, 32(12):1941-1944.

LIANG G L, SHENG X L. Research on wideband FM signal detection technology based on WVD-HT[J]. Atca Electronica Sinica, 2011, 32(12): 1941-1944.

[2] WANG H W, FAN X Y, CHEN Y, et al. Wigner-hough transform based on slice’s entropy and its application to multi-LFM signal detection[J]. Journal of Systems Engineering and Electronics, 2017, 28(4):634-642.

[3] DING Y F, SUN L, ZHANG H Y, et al. A multi-component LFM signal parameters estimation method using STFT and Zoom-FRFT[C]∥Proc.of the 8th IEEE International Conference on Communication Software and Networks,2016:112-117.

[4] DUAN Y, WANG J Z, SU S Y, et al. Detection of LFM signals in low SNR based on STFT and wavelet denoising[C]∥Proc.of the International Conference on Audio, Language and Image Processing, 2014:921-925.

[5] MA X, LIU D, SHAN Y. Intra-pulse modulation recognition using short-time ramanujan Fourier transform spectrogram[J]. Eurasip Journal on Advances in Signal Processing, 2017,2017(1):42.

[6] 崔化超,周胜增,蒋小勇. 水声脉冲信号实时检测估计软件的设计与实现[J]. 声学技术, 2015, 34(4): 74-77.

CUI H C, ZHOU S Z, JIANG X Y. Design and realization of real-time detection and estimation software for underwater acoustic pulse signal[J].Technical Acoustics, 2015,34(4):74-77.

[7] 黄冠钦,杨坤德,马远良. 微弱信号的自适应相干累积检测[J].声学技术, 2011,30(3): 198-200.

HUANG G Q, YANG K D, MA Y L. Adaptive coherent accumulation detection of weak signal[J]. Technical Acoustics, 2011, 30(3): 198-200.

[8] 王晓燕,方世良,朱志峰. 基于ST-FRFT的非合作水声脉冲信号检测方法[J]. 信号处理, 2011, 21(8): 1271-1278.

WANG X Y, FANG S L, ZHU Z F. Non-cooperative underwater acoustic pulse signal detection method based on ST-FRFT[J]. Journal of Signal Processing, 2011, 21(8): 1271-1278.

[9] CHEN Y L, GUO L X, GONG Z X. The concise fractional Fourier transform and its application in detection and parameter estimation of the linear frequency-modulated signal[J].Chinese Journal of Acustica, 2017(1): 70-86.

[10] ZHANG Z C, WANG H Y, LIU Z G, et al. An new LFM detection algorithm based on ADTR-FrFT for active sonar system[C]∥Proc.of the IEEE International Conference on Signal Processing, Communications and Computing, 2017:1-5.

[11] SHI H, XIONG J, ZHOU C, et al. A new recognition and classification algorithm of underwater acoustic signals based on multi-domain features combination[C]∥Proc.of the Ocean Acoustics, 2016: 1-7.

[12] HOW J, HATZINAKOS D. Impulsive noise modeling with stable distributions in fading environments[C]∥Proc.of the Statistical Signal and Array Processing, 1996: 140-140.

[13] LAGUNA S G, LOPEZ G M. On the use of alpha-stable distributions in noise modeling for PLC[J]. IEEE Trans.on Power Delivery, 2015, 30(4):1863-1870.

[14] CHEN Z, GENG X, YIN F. A harmonic suppression method based on fractional lower order statistics for power system[J]. IEEE Trans.on Industrial Electronics,2016,63(6):3745-3755.

[15] MAHMOOD A, CHITRE M, Armand M A. Maximum-likelihood detection performance of uncoded OFDM in impulsive noise[C]∥Proc.of the IEEE Global Communications Conference, 2013: 3516-3521

[16] QIU T S, ZHANG X. Statistical signal processing: non-gaussion signal processing and applications[M].Beijing: Electronic Industry Press, 2004: 169-172.

[17] 陈文武,蔡征宇,陈如山,等.脉冲噪声下基于Robust STFT的信号检测与参数估计[J].南京理工大学学报,2012,36(2):328-331.

CHEN W W, CAI Z Y, CHEN R S, et al. Signal detection and parameter estimation based on robust STFT under impulse noise[J]. Journal of Nanjing University of Science and Technology, 2012, 36(2): 328-331.

[18] 金艳,高舵,姬红兵.α稳定分布噪声下基于稳健S变换的LFM信号参数估计[J].系统工程与电子技术,2017, 39(4):693-699.

JIN Y, GAO D, JI H B. Parameter estimation of LFM signal based on robust S transform inαstable distribution noise[J]. Systems Engineering and Electronics, 2017, 39(4):693-699.

[19] 金艳,胡碧昕,姬红兵.α稳定分布噪声下基于最优L-柯西加权的LFM信号参数估计[J].系统工程与电子技术,2016,38(7): 1488-1495.

JIN Y, HU B X, JI H B. Parameter estimation of LFM signal based on optimal L-Cauchy weighted method inαstable distribution noise[J]. Systems Engineering and Electronics, 2016, 38(7):1488-1495.

[20] 张俊林.α稳定分布噪声下通信信号调制分析技术研究[D].郑州: 信息工程大学, 2005.

ZHENG J L. Research on communication signal modulation analysis technology under alpha stable distributed noise[D]. Zhengzhou:Information Engineering University, 2005.

[21] OZAKTAS H M, ARIKAN O, KUTAY M A, et al. Digital computation of the fractional Fourier transform[J]. IEEE Trans.on Signal Processing, 1996, 44(9): 2141-2150.

[22] 陶然,邓兵,王越. 分数阶傅里叶变换及其应用[M].北京: 清华大学出版社, 2009: 13-25.

TAO R, DENG B, WANG Y. Fractional Fourier transform and its application[M]. Beijing:Tsinghua University Press, 2009: 13-25.

[23] VAPNIK V. The nature of statistical learning theory[M].New York: Springer, 1995:142-165.

[24] ZHAO H, CHEN H, NGUYEN T. Stratified over-sampling bagging method for random forests on imblanced data[M]. Switzerland: Springer International Publishing, 2016:46-60.

[25] VLUYMANS S, TARRAGOD S, SAEYS Y. Fuzzy rough classifiers for class imbalanced multi-instance data[J].Pattern Recognition, 2016, 53(C):36-45.

[26] LIU ALEXANDER, GHOSH J, MARTIN C. Generative oversampling for mining imbalanced datasets[C]∥Proc.of the International Conference on Data Mining, 2007:66-72.

[27] China Argo Real-time Data Center. The International Argo Project[EB/OL].[2017-8-08].http:∥www.argo.org.cn/data/argo.php/.