基于反馈证据冲突度的概率转换

关 欣, 刘海桥, 衣 晓, 赵 静

(海军航空工程学院电子信息工程系, 山东 烟台 264001)

0 引 言

不确定推理是多源信息融合与人工智能领域处理不确定数据的有效手段,主要方法有贝叶斯推理[1]、D-S证据理论[2-4]、D-S理论(Dezert-Smarandache theory, DSmT)[5-6]、模糊逻辑推理、粗糙集理论等[7]。

而对于证据理论还存在诸多课题等待进一步研究,其中包括基本概率赋值(basic probability assignment, BPA)的获取、相关证据的融合、冲突证据的融合[8-13]、证据决策等相关问题的研究,随着研究进一步深入,目标识别框架由概率框架拓展到幂集框架和超幂集框架等广义幂集框架,广义幂集框架的势不断增大,信度赋值过于分散,决策过程相对复杂,传统的基于BPA的决策方法不能对目标有效识别。而概率推理方法具有较强理论基础,所以国内外学者开展了概率转换方法研究,将广义幂集框架下的信度赋值映射到单子集识别框架形成概率,利用概率推理手段对目标进行识别。

文献[14-15]率先提出基于可传递信度模型(transferable belief model, TBM)中的Pignistic概率转换(pignistic probability transform, PPT),将广义幂集框架下的BPA根据命题的势均分到单子集命题,该方法过于粗糙,没有考虑单子集命题权重;文献[16-18]结合信任函数和似真度函数对单子集命题的权重进行改进,提出多种改进算法,但提出的系列算法中多采用单一指标进行决策分析;文献[19]将信任函数与似真度函数相结合对转换公式进行改进,但构造的公式没有利用命题的势;文献[20-21]引入命题的势,给出新的改进公式,但是缺乏合理的评价指标;文献[22]在pignistic概率转换的基础上,提出多尺度概率转换(multiscale probability, MulP)函数,该公式引入Tsallis信息熵,对PPT进行了一般化表达,但同样没有给出合理的评价指标;文献[23]在研究冲突证据之间融合问题时,提出改进型概率转换公式,对于转化公式的合理性,同样,文章只给出算例分析;文献[24]在D-S证据融合中,关于组合规则选取和概率转换方法选取之间的关联性进行了深入研究;文献[25]引入有序加权平均的思想,基于有序可视图(ordered visibility graph, OVG)给出新的概率转换公式,该方法基于BPAs给出OVG,从而计算出每个元素的权重,能够一定程度上得到有效的概率转换结果。

上述概率转换公式方法的给出过程较为主观,概率转换方法缺乏严密性,本文首先从多种概率转换公式出发,研究概率转换规律,给出统一的概率转换公式。

概率转换的另一个研究焦点在于,如何对概率转换公式进行合理评判,以论证转换的合理性。概率转换效果好坏,应分析转换后的概率能否有效表征原有的证据,即转换后的概率向量与原有的证据向量关联性大小。概率转换公式的评价多采用文献[12]提出的概率信息容量(probability information content, PIC),而PIC本质上是对转换后概率信息熵的归一化。在BPA不确定度度量问题的研究中,多引入信息熵的概念。学者先后提出诸多信息熵的概念[26-29],其中文献[29]提出的新的Deng熵,Deng熵引入元素的势,将元素本身的不确定度也考虑在内,使得对BPA不确定度的度量更加合理。但是这些熵信息并不能很好地衡量证据之间的关联度,只能反映证据的决策能力,并不能反映概率转换的合理性。

鉴于此,文献[30]在关联系数基础上,提出证据关联系数,给出最优化转换方法,使转换概率与原证据关联系数最大,但是,该方法提出的证据关联系数衡量的是转换概率与原证据当中单元素命题之间的关联程度,丢失了多元素命题的信息量,并不能很好的度量转换概率与原证据之间的关联程度。对于2个证据之间的冲突度的度量研究,是一类超维函数求解问题,而且维度随着识别框架的变化而变化,所以现有的冲突度量函数都很难表征证据之间的冲突度。鉴于此,本文引入了现代优化算法。通过构造新的基于反馈证据冲突度的评价方法;在统一的概率转换公式框架下,基于最小反馈冲突度,利用遗传算法求解出新的转换概率;最后结合仿真分析验证本文方法合理性。

1 理论基础

主观贝叶斯方法是不确定推理最初使用的方法,该方法基于概率论中的贝叶斯理论进行不确定推理,具有较强理论基础,但是在处理不确定数据过程中,用概率来表示不确定信息的贝叶斯方法没有用信度表示不确定方法的证据理论有效[31]。D-S证据理论是对主观贝叶斯方法的推广[2-3],这种与推广具体表现在对识别框架的推广,假设研究对象X的所有可能取值都在论域集合中,Ω内所有元素互斥,则称Ω为一识别框架。在贝叶斯框架下,命题Ai∈Ω互相独立,而D-S证据理论将识别框架推广到了幂集,命题Ai,Aj∈2Ω,则Ai∪Aj∈2Ω,即幂集2Ω在并运算下封闭。假设Ω为一识别框架,映射m:2Ω→[0,1]在满足

(1)

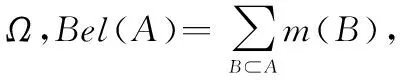
构建上述信度函数的最终目的是决策,从而形成有效评估,但是由于信度表示信息的不确定性,使得决策缺乏有效的理论基础,同时也不符合人的主观认知。鉴于此,文献[14-15]进一步证实了概率转换的有效性,并将决策分为2个层,credal层和pignistic层。在credal层,建立各种模型,完成对不确定信息的表示;在pignistic层,完成对信度的概率转换,概率转换要求命题Ai转换后得到的概率应该落在原命题Ai的信任区间内,同时转换后的概率在单元素框架Ω内满足归一化要求,即满足

(2)

与传统的决策相比,基于pignistic概率转换的决策方法更符合人的决策思维,同时拉大了不同元素之间的信度赋值,有效提高识别率。

2 概率转换公式的统一表达式

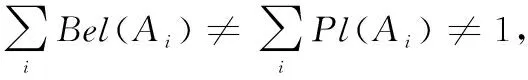
2.1 Bel或Bel(A)类方法的统一概率转换公式

Bel(A)、Pl(A)不具备归一化要求,单纯基于Bel或Pl的概率转换公式相对较少。通过对现有概率转换公式分析,给出这一类型的统一的概率转换公式

(3)

其中

BP(Ai)=α1Bel(Ai)+(1-α2)Pl(Ai)

(4)

(5)

式中,αi为[0,1]区间上的常数。

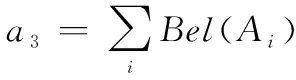
2.2 BPA类方法的统一概率转换公式

m(Ai)具备归一化要求,转换公式更直观,多数转换公式基于这一类模型。通过对现有概率转换公式分析,给出这一类型的统一的概率转换公式

(6)

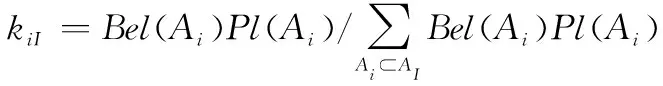
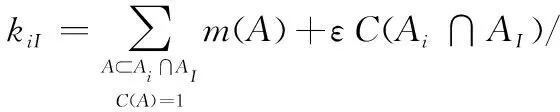
文献[21]在DSmP的基础上,基于分层概率转换思想,提出Hierarchical DSmP(HDSmP),虽然HDSmP公式利用递推的形式给出,但分析不难发现也是第二类概率转换模型,考虑多元素命题A(k)转换给Ai⊂A(k)的概率

(7)

需通过分层递推求解得到。

文献[22]在pignistic概率转换的基础上,提出多尺度概率转换MulP,该公式引入Tsallis信息熵q对PPT进行了一般化表达:

其中,m(φ)≠0,可以看出

当q=0时,MulP便退化为pignistic概率转换[14]。

3 基于反馈证据冲突度的概率转换公式

3.1 新的基于反馈证据冲突度的概率转换表达式

3.1.1 基于反馈证据冲突度的概率转换评价方法

概率转换问题讨论焦点在于如何设计合理的转换公式,本文将提出新的基于最小反馈证据冲突度的概率转换评价方法。

概率转换将原有的广义幂集框架下的信任分配转换到单元素框架下的概率,转换后的概率应该与原证据具有很高的相似度。本文构造反馈证据冲突度的指标来衡量概率转换的优劣,先将证据进行概率转换,然后将转换概率与原基本概率赋值融合,得到反馈证据,最后计算反馈证据与原证据之间的冲突度,冲突度越小,概率转换公式转换效果越优,如图1所示。

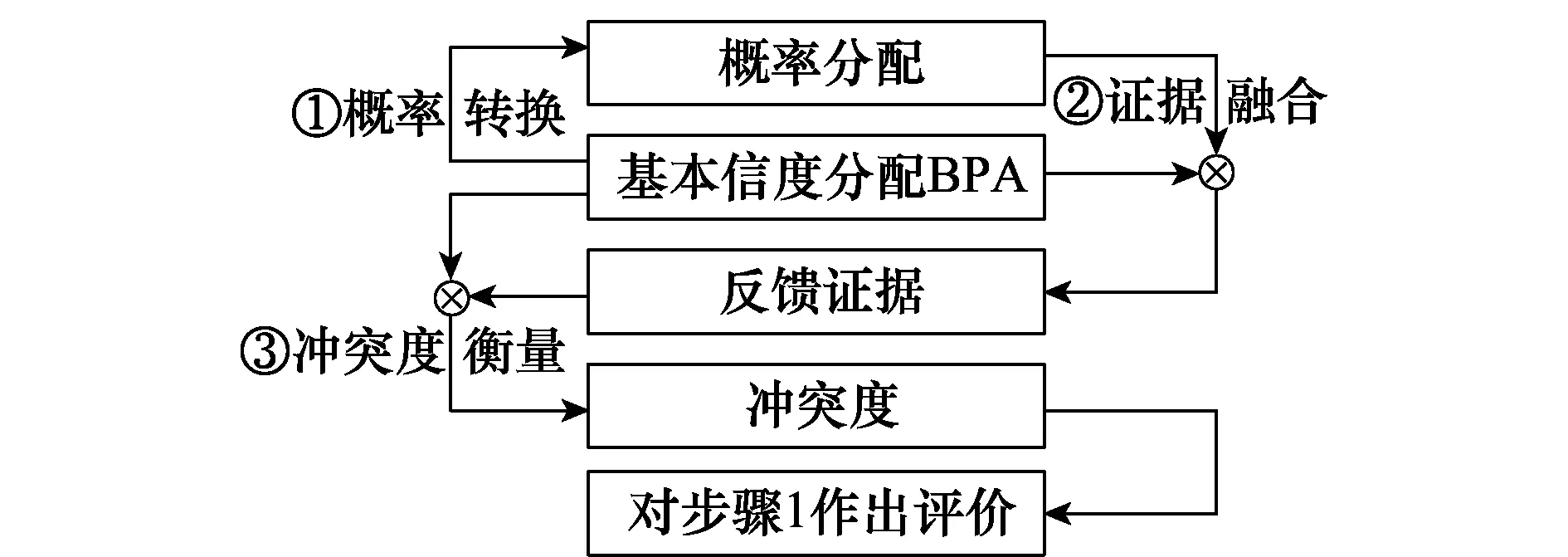
图1 基于反馈证据冲突度的概率转换评价方法流程图Fig.1 Flow diagram of the conflict degree of feedback evidence

3.1.2 最小反馈证据冲突度概率转换表达式

结合流程图1,给出基于最小反馈冲突度的概率转换表达式(8),其中,m′为转换概率,⊗表示混合DSmT组合规则。

从流程图中可以看出,基于反馈证据冲突度的概率转换方法有两层反馈,第1层是通过证据融合规则,得到反馈证据;第2层是通过冲突度量函数得到冲突度,所以基于反馈证据冲突度的评价标准效果的好坏,取决于融合规则和冲突度量函数选取的优劣,下面对这2个要素分别进行分析与选取。

mindcf(m1,m2)

(8)

3.1.3 概率转换表达式中证据融合规则的选取

步骤2中的证据融合规则的选取决定了概率转换评价效果的好坏,分析流程图,可以知道,选取的证据融合规则需具备以下要素:能够有效的表达两条证据的综合信度;融合后的识别框架与原证据识别框架保持一致。随着不确定推理的研究不断地深入,文献[2]提出经典的Dempster组合规则

(9)

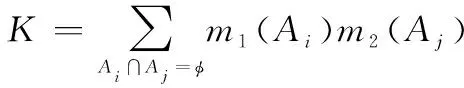
Dempster组合规则在处理冲突量时采用了归一化手段,但是由于冲突系数K的存在,使得Dempster组合规则在处理冲突信息时,产生反直觉效果,不利于决策。其次,分析Dempster组合规则发现,证据与转换概率进行组合时,由于转换概率都是单元素集,所以在Dempster组合规则下,步骤2融合后的识别框架为单元素集,不利于后续的证据冲突度的度量,失去证据融合的意义。D-S证据组合规则有很多的改进规则,其中具有代表性的是DSmT[21]:

(10)

式中,Φ(A)是命题A的特征非空函数,混合DSmT模型的约束条件就是原证据的信任赋值空间。由于DSmT证据理论能有效融合冲突证据,并且,通过混合DSmT模型,融合后的反馈证据与原证据理论有着相同的识别框架,对于步骤2证据融合方法,本文选取混合DSmT证据融合模型。

3.1.4 概率转换表达式中冲突度量函数的选取

衡量2个信度赋值之间的冲突度,便是求解2个向量之间“距离”的算法研究。在线性空间V中,对于任意的向量x,都存在着非负实数‖x‖与之对应,并满足以下要求:‖x‖≥0,‖x‖=0当且仅当x=0,‖kx‖=|k|·‖x‖,‖x+y‖≤‖x‖+‖y‖,则称‖x‖为向量x的范数。

其中应用比较广泛的有文献[32]提出的是证据距离:

(11)

3.2 基于反馈证据冲突度的概率转换方法实现

对式(8)优化问题进行求解。由于规划方程中的约束条件有概率转换运算和混合DSmT运算,这2种运算都不是连续的,所以,上述优化问题需要通过现代优化技术解决,本文将采用理论比较成熟、应用比较广泛的遗传算法解决上述优化问题。具体算法流程图如图2所示,首先构造初始“种群”,使算法能够快速收敛,初始种群数据通过pignistic概率转换获取得到,种群的数量与识别框架的势有关;然后进过复制、交叉、变异等操作,直到数据收敛,交叉和变换都有相应的执行概率pc、pm,以模拟生物进化过程;适应度函数用反馈证据冲突度衡量。

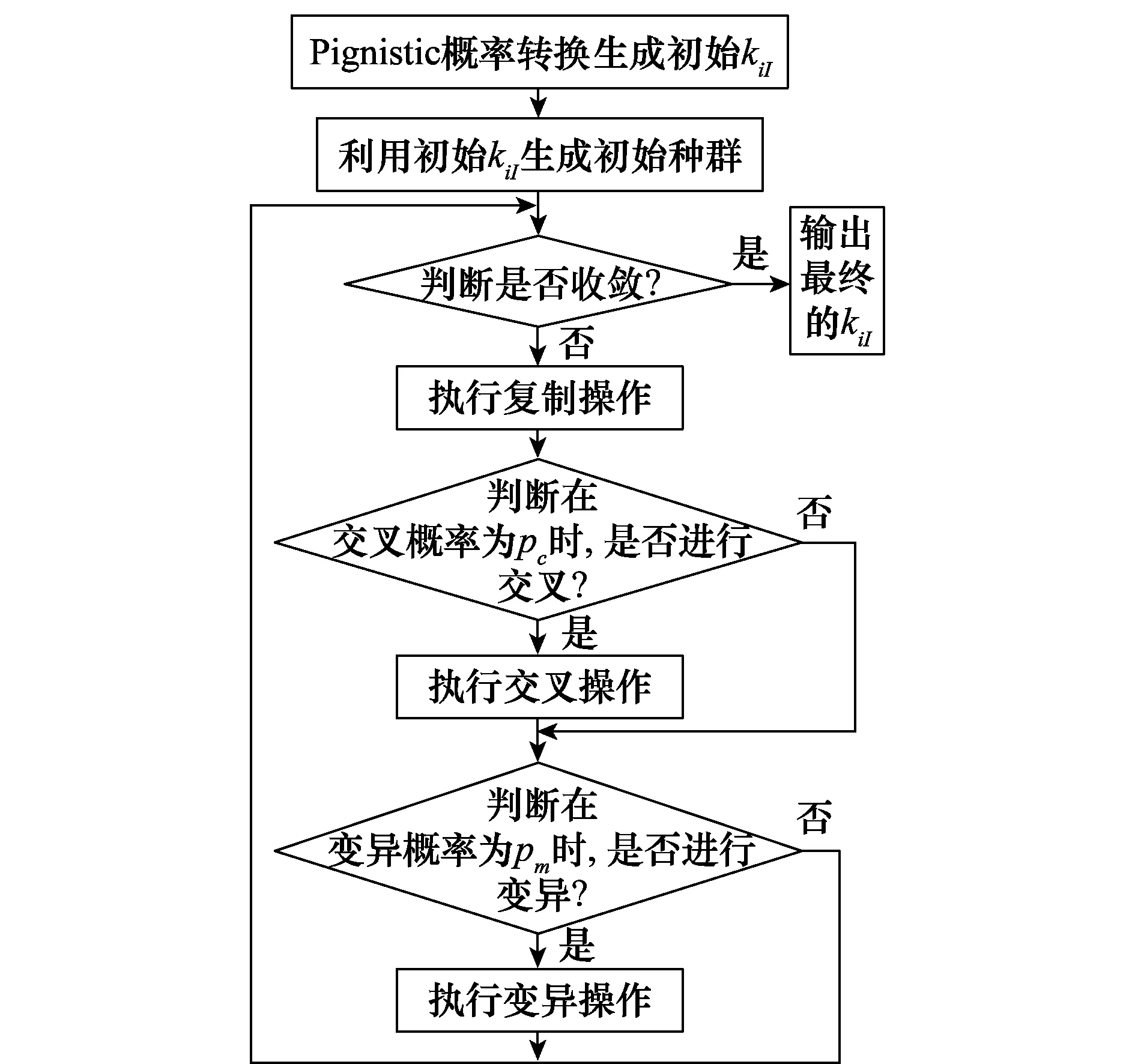
图2 基于遗传算法求解概率转换流程图Fig.2 Flow diagram of the probability transformation

具体实现步骤如下:

步骤1生成初始种群

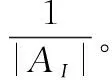
步骤2构建种群

步骤3染色体编码

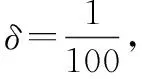
步骤4个体适应度评价

个体适应度评价方法利用反馈证据冲突度dcf,计算种群每一个体反馈证据冲突度,判断是否收敛,如果收敛,输出概率转换结果;如果不收敛,进行升序排序,淘汰后N/2的个体,形成新的种群。

步骤5繁衍复制

步骤6染色体交叉运算

图3 染色体交叉运算Fig.3 Chromosome crossover operation

步骤7染色体变异运算

染色体复制过程中还存在变异的可能,如图4所示。为模拟这一过程,随机选取染色体的突变点进行变异运算,变异概率pm=0.05,同样对运算结果进行归一化。

图4 染色体变异运算Fig.4 Chromosome mutation operation

步骤8返回步骤4。

4 算例分析

4.1 对反馈证据冲突度评价方法的算例分析

算例1假设识别框架Ω={a,b,c,ab,ac,bc,abc},基本概率赋值定义如下m(a)=m(b)=m(c)=0.2,m(ab)=m(ac)=m(bc)=m(abc)=0.1,分别用不同的概率转换公式对其进行转换,得到相同的转换概率m′(a)=m′(b)=m′(c)=1/3。再分别用不同的评价方法对转换结果进行评价,得到表1数据。算例中基本概率赋值对a、b、c的信任程度一样,概率转换应该给予a、b、c相同的转换概率,所以现有概率转换方法都赋予a、b、c转换概率1/3是合理的,不同评价方法对此概率转换因给出最优评价。

表1 算例1概率转换评价结果

但是,基于信息熵的评价方法(越小越好)给出最差的评价,因为信息熵反应的是证据的决策能力,当a,b,c具有相同的转换概率时,无法作出决策,与正确评价刚好相反;本文基于反馈证据冲突度的评价方法(越小越好)给出较优的评价结果,能够正确衡量概率转换的效果;而基于关联系数评价方法(越大越好)和本文评价方法一样给出较优的评价结果,因为关联系数衡量的是转换概率与原证据中单元素命题之间的关联程度,该算例中原证据单元素命题a,b,c的信度都为0.2,所以基于关联系数评价方法给出较优评价,但这并不能反应关联系数评价方法的优越性,下面看算例2。

算例2假设识别框架Ω={a,b,c,ab,ac,bc},基本概率赋值定义如下:

m(a)=0.015,m(b)=0.015,m(c)=0.07

m(ab)=0.3,m(ac)=0.3,m(bc)=0.3

分别用不同的概率转换公式对其进行转换,并算出不同评价方法下的转换效果,如表2所示。

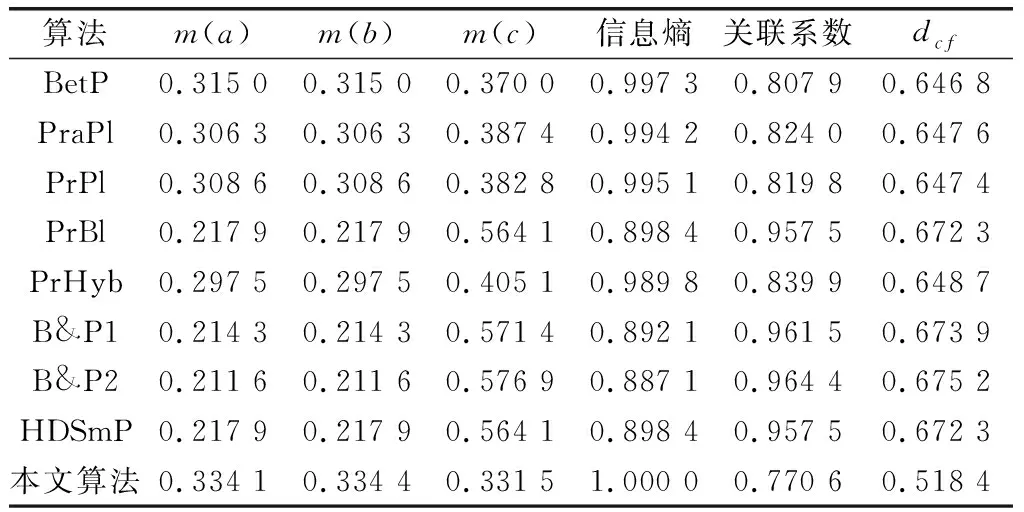
表2 算例2实验结果

该算例中基本概率赋值,单元素命题的信度很低,多元素命题给予a,b,c的信度相等,所以转换结果应该显示a,b的概率相等,c的概率略高。从融合结果看,这几种融合算法都赋予c命题过高的概率,效果不是很理想。基于信息熵的评价方法显示,BetP,PraPl,PrPl法转换效果较差,但是,通过分析可以发现,相比于其他算法,这3种算法更接近基本概率赋值的设定,原因和算例1一样,信息熵不能反映转换概率的好坏;基于关联系数的评价方法认为几种概率转换效果很好,原因在于转换后a,b,c概率之间比例与原证据中单元素信度之间比例相似,所以给出错误评判;而本文提出的反馈证据冲突度显示,几种转换方法都不是很好,相比较而言,BetP,PraPl,PrPl法更优于其他几种算法。通过算例分析可以看到反馈证据冲突度相比于其他的评价方法能够更好地衡量概率转换的效果。

4.2 基于反馈证据冲突度的概率转换仿真分析

假设识别框架Ω={a,b,c,ab,bc,abc},基本概率赋值定义如下:

m(a)=0.1,m(b)=0.1,m(c)=0.2

m(ab)=0.2,m(bc)=0.1,m(abc)=0.3

基于遗传算法求解最小反馈证据冲突度的概率分配,算法迭代过程如图5所示。横坐标表示遗传算法中“种群”繁衍代数,种群指规划方程中比例系数kiI;纵坐标表示适应度函数,本文用反馈证据冲突度dcf表示种群的适应度。可以看出,当繁衍代数为1 000次时,系统处于收敛状态;图中的多个阶跃点是由于种群变异产生,向上阶跃表明变异后的个体是劣质的,向下阶跃表明变异后个体是优异的。

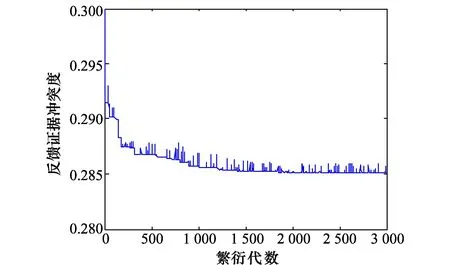
图5 遗传算法迭代过程Fig.5 Iteration process of genetic algorithm

分别用不同的概率转换公式对算例进行转换,并算出转换效果,如表3所示。

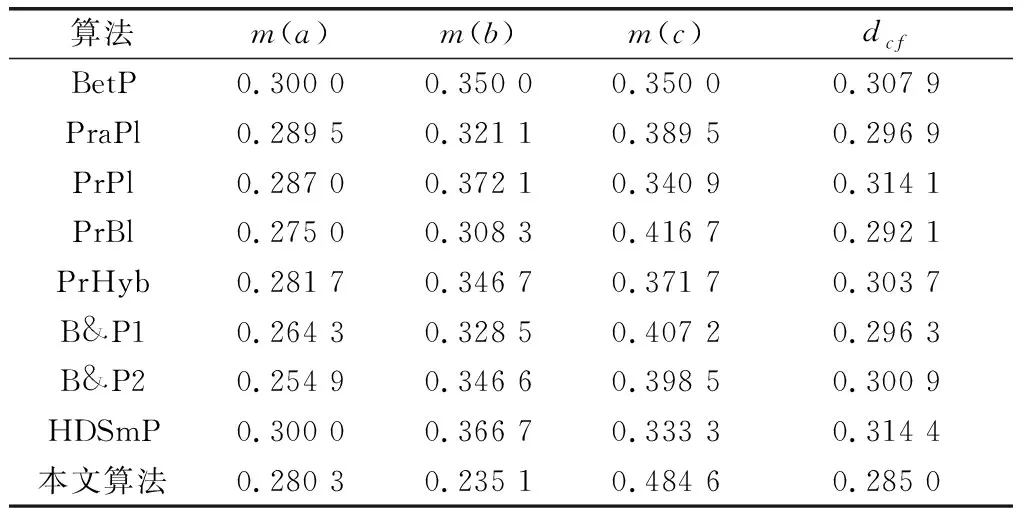
表3 各种概率转换结果对比

对表3中数据进行对比,发现本文算法能求解出更合理的概率分配,因为不同改进型概率转换算法求解过程较为主观,先定义概率转换公式,然后根据转换结果验证算法合理性,这很难得到最优转换概率;同时经典的pignistic概率转换方式下的转换概率不一定比其他改进型的概率转换方式差,只是单纯的从数学公式角度分析,改进型的概率转换公式比经典的pignistic概率转换公式更加合理。

最后,利用基于反馈证据冲突度的概率转换方法对算例2的数据进行算例分析,结果如表2所示,3个单元素得到的转换后概率都接近1/3,符合直觉判断结果。而从评价指标可以看出,信息熵的评价指标为1,最差,因为当元素的置信度相同时,无法进行决策;关联系数也给出相对其他转换方法较差的评价结果,因为该算例中单元素赋值太小,失去意义,而关联系数衡量的是转换概率与原证据当中单子集命题之间的关联程度,没考虑多子集命题的信息量,因此不能很好的度量转换效果;本文提出的反馈证据冲突量相对于其他算法给出较好的评价结果,验证了本文所提方法的有效性。

5 结 论

概率转换是不确定推理中有效决策方法之一,合理的概率转换可以有效地避免不准确的估计与决策。本文首先从结构组成上分析现有的多种概率转换公式,给出两类统一的概率转换公式;然后构造反馈证据冲突度评价指标,利用转换概率与原基本概率赋值经过DSmT融合规则得到反馈证据,计算反馈证据与原证据之间冲突度,有效衡量概率转换效果;继而利用统一的概率转换公式框架,在最小反馈证据冲突度的约束条件下,利用遗传算法求解出最优的转换概率;最后分别对基于反馈证据冲突度的评价方法和概率转换的实现进行算例分析,表明了算法的合理性。

参考文献：

[1] LUCAS P J, HOMMERSOM A. Modeling the interactions between discrete and continuous causal factors in bayesian networks[J]. International Journal of Intelligent Systems, 2015, 30(3): 209-235.

[2] DEMPSTER A P. Upper and lower probabilities induced by a multivalued mapping[J]. Annals of Mathematical Statistics, 1967, 38(2): 325-339.

[3] DENG Y. Generalized evidence theory[J]. Applied Intelligence, 2015, 43(3):530-543.

[4] YAGER R R, ALAJLAN N. Dempster-Shafer belief structures for decision making under uncertainty[J]. Knowledge Based Systems, 2015,80(C): 58-66.

[5] DEZERT J, SMARANDACHE F. Advances and applications of DSmT for information fusion collected works[M]. 4th ed. Rehoboth: American Research Press, 2015.

[6] HAN D, DEZERT J, DUAN Z. Evaluation of probability transformations of belief functions for decision making[J]. IEEE Trans.on Systems Man & Cybernetics-Part A: Systems,2016,46(1):1-18.

[7] YANG Y, HAN D. A new distance-based total uncertainty measure in the theory of belief functions[J]. Knowledge-Based Systems, 2016, 94: 114-123.

[8] HAN D, DEZERT J, YANG Y. Belief interval-based distance measures in the theory of belief functions[J]. IEEE Trans.on Systems Man & Cybernetics Systems, 2016,PP(99): 1-18.

[9] QIAN J, GUO X F, DENG Y. A novel method for combining conflicting evidences based on information entropy[J]. Applied Intelligence, 2017, 46(4): 876-888.

[10] YU C, YANG J, YANG D, et al. An improved conflicting evidence combination approach based on a new supporting probability distance[J]. Expert Systems with Applications, 2015, 42(12): 5139-5149.

[11] SMARANDACHE F, DEZERT J. Modified PCR rules of combination with degrees of intersections[C]∥Proc.of the International Conference on Information Fusion, 2015: 2100-2107.

[12] JIANG W, LUO Y, QIN X, et al. An improved method to rank generalized fuzzy numbers with different left heights and right heights[J]. Journal of Intelligent and Fuzzy Systems, 2015, 28(5): 2343-2355.

[13] JIANG W, WEI B, QIN X, et al. Sensor data fusion based on a new conflict measure[J]. Mathematical Problems in Engineering, 2016: 1-11.

[14] SMETS P, KENNES R. The transferable belief model[J]. Artifieial Intelligenee, 1994, 66(4): 191 -234.

[15] SMETS P. Decision making in the TBM: the neeessity of the pignistic transformation[J]. International Journal of Approximate Reasoning, 2005, 38(2): 133-147.

[16] SUDANO J J. The system probability information content (PIC) relationship to contributing components, combining independent multi-source beliefs, hybrid and pedigree pignistic probabilities[C]∥Proc.of the International Conference on Information Fusion, 2002: 1277-1283.

[17] SUDANO J J. Yet another paradigm illustrating evidence fusion(YAPIEF)[C]∥Proc.of the International Conference on Information Fusion, 2007:1-7.

[18] SUDANO J J. Pignistic probability transforms for mixes of low-and high-probability events[C]∥Proc.of the 4th International Conference on Information Fusion, 2001: 23-7.

[19] 潘巍, 王阳生, 杨宏戟. Pignistic概率转换算法设计[J]. 计算机工程与应用, 2005, 31(4): 20-25.

PAN W, WANG Y S, YANG H J. Algorithm design of pignistic probability transforms[J]. Computer Engineering and Applications, 2005, 31(4): 20-25.

[20] DEZERT J, SMARANDACHE F. A new probabilistic transformation of belief mass assignment[C]∥Proc.of the International Conference on Information Fusion, 2008: 1-8.

[21] DEZERT J, HAN D, LIU Z G, et al. Hierarchical DSmP transformation for decision-making under uncertainty[C]∥Proc.of the International Conference on Information Fusion, 2012: 294-301.

[22] LI M, LU X, ZHANG Q, et al. Multiscale probability transformation of basic probability assignment[J]. Mathematical Problems in Engineering, 2014,2014: 1-6.

[23] MA M, AN J. Combination of evidence with different weighting factors: a novel probabilistic-based dissimilarity measure approach[J]. Journal of Sensors, 2015, 2015(2): 1-9.

[24] CINICIOGLU E N. Decision making with consonant belief functions: Discrepancy resulting with the probability transformation method used[J]. Yugoslav Journal of Operations Research, 2014, 24(3): 359-370.

[25] LI M, ZHANG Q, DENG Y, et al. A new probability transformation based on the ordered visibility graph[J]. International Journal of Intelligent Systems, 2016, 31(1): 44-67.

[26] DU W, GAO Y, LIU C, et al. Adequate is better: particle swarm optimization with limited-information[J]. Applied Mathematics and Computation, 2015, 268: 832-838.

[27] DU W, YING W, YAN G, et al. Heterogeneous strategy particle swarm optimization[J]. IEEE Trans.on Circuits and Systems Ii-express Briefs, 2017, 64(4): 467-471.

[28] DU W, ZHOU X, LORDAN O, et al. Analysis of the Chinese airline network as multi-layer networks[J]. Transportation Research Part E-logistics and Transportation Review, 2016, 89(89): 108-116.

[29] DENG Y. Deng entropy: a generalized shannon entropy to measure uncertainty[J]. Chaos, Solitons & Fractals, 2016, 91: 549-553.

[30] 许培达, 韩德强, 邓勇. 一种基本概率赋值转换为概率的最优化方法[J]. 电子学报, 2011, 39(3A): 121-125.

XU P D, HAN D Q, DENG Y. An optimal transformation of basic probability assignment to probability[J]. Acta Electronica Sinica, 2011, 39(3A): 121-125.

[31] 蒋雯, 张安, 邓勇. 基于区间信息的基本概率赋值转换概率方法及应用[J]. 西北工业大学学报, 2011, 29(1): 44-48.

JIANG W, ZHANG A, DENG Y. Proposing interval probability transform(IPT) method for decision making and its application[J]. Journal of Northwestern Polytechnical University, 2011, 29(1): 44-48.

[32] JOUSSELME A, GRENIER D, BOSSE E, et al. A new distance between two bodies of evidence[J]. Information Fusion, 2001, 2(2): 91-101.