多小区全双工MIMO系统中干扰对齐方案

景小荣, 张翠翠

(1. 重庆邮电大学通信与信息工程学院, 重庆 400065; 2. 移动通信技术重庆市重点实验室, 重庆 400065)

0 引 言

在全双工多输入多输出(full-duplex multiple-input multiple-output,FD-MIMO)无线系统中,基站在同时隙同频段内实现下行信号发送和上行信号接收。在通信过程中,系统中不但存在传统的上/下行多输入多输出(multiple-input multiple-output,MIMO)信道间干扰,而且还存在基站发射信号对自身接收信号造成的自干扰(self-interference,SI)和上行用户发送对下行用户接收所造成的干扰(interference between uplink users transmitting and downlink users receiving,I-UuT-DuR),这些干扰的存在成为制约FD-MIMO技术商业化应用的主要障碍。以往针对全双工(full-duplex, FD)技术的研究通常只专注于SI的消除,根据对最新相关研究成果的调研,目前 SI消除方面已取得相当丰硕的理论成果[1-2]。而针对FD-MIMO系统的复杂干扰消除技术的研究,却相对甚少。文献[3-4]在消除SI的基础上,以最大化频谱效率和能量效率为目标,通过采用迭代优化预编码技术,尽管有效地提升了系统的性能,但均忽略了I-UuT-DuR。在实际FD-MIMO通信场景中,I-UuT-DuR对系统性能的影响是不容忽视的。

在无线通信系统中,干扰对齐(interference alignment,IA)技术[5-7]因其适用范围广、干扰处理能力强等优点而被业界深入研究。于是,面对FD-MIMO系统中如此复杂的干扰问题, 研究IA在FD-MIMO系统中的具体实现方案将具有重要的现实意义。截止目前,IA在FD-MIMO无线系统中的研究工作主要分为两类,一类研究工作主要集中在IA在FD-MIMO无线系统中的可行性方面,另外一类研究工作主要集中在IA在FD-MIMO无线系统中的具体设计及实现方面。

IA技术在FD-MIMO无线系统中的可行性研究方面,文献[8]针对单小区FD-MIMO系统,分析了FD基站FD用户(FD based station FD user,FD-BS-FD-User)模型下,IA实现的充要条件,同时给出了在该模型下对称系统的可达自由度。文献[9]从理论上分析了线性IA消除多小区FD-MIMO系统中I-UuT-DuR的可行性,同时给出相对于半双工(half-duplex, HD)系统,有/无上行协作、用户数目足够大/用户数有限等情况下,FD复用增益的变化情况。基于时域符号扩展,文献[10-11]分析了单小区FD系统中IA的可行性,同时,文献[10]给出了FD基站HD用户(FD based station HD user，FD-BS-HD-User)模式下,多输入单输出(multiple-input single-output,MISO)系统的自由度,分析了全局/部分信道状态信息(channel state information,CSI)条件下IA的可行性;而文献[11]则分别分析了FD-BS-FD-User和FD-BS-HD-User两种模型下系统可达自由度上限。文献[12]针对单小区FD-BS-HD-User MISO系统,在基站端有/无CSI条件下,利用盲IA技术实现I-UuT-DuR的抑制。总之,由于FD-MIMO IA算法设计相对比较复杂,而现有关于FD-MIMO IA研究方面的文献相对比较少,主要专注于单小区场景,且假设系统中SI已被完全消除。

最近,文献[13]在非理想SI消除条件下,针对FD-BS-HD-User模型,提出闭式线性IA设计方案,并分析了系统的可达自由度,进一步将其推广到FD-BS-FD-User模型,但该方案仅考虑了小区间不存在干扰的理想情况。受文献[13]启发,本文在非理想SI消除条件下,同时考虑实际小区间干扰问题,提出了一种适用于多小区多用户FD-MIMO系统的空域IA方案。文中首先分析了多小区多用户FD-MIMO系统线性IA实现的可行性条件,提出一种多对一(many-to-one,MTO)线性IA算法,该算法可有效地消除上/下行小区间干扰及小区内用户间干扰;然后,基于残留I-UuT-DuR构建目标函数,通过构造下行用户内层接收干扰抑制矩阵辅助函数,将目标函数转化为仅与上行用内层户预编码矩阵相关的代价函数,进而基于格拉斯曼流形上的最速梯度下降法迭代求解预编码矩阵。数值仿真结果表明,该方案可有效地解决多小区多用户FD-MIMO系统中复杂的干扰问题,从而提高了系统的整体性能。需要进一步指出的是,该方案中,在FD-BS-FD-User模型下,为了消除上/下行小区间干扰及小区内用户间干扰,所求下行预编码矩阵和外层接收干扰抑制矩阵可通过上行接收干扰抑制矩阵和外层预编码矩阵直接求得,此时,MTO线性IA算法仅需基站知道上行CSI,而无需CSI反馈,使得该方案在FD-BS-FD-User模型下的复杂度大幅度下降。

符号说明:用‖A‖F、A*、AT、AH和A†分别表示矩阵A的Frobenius范数、复共轭变换、转置变换、共轭转置变换和广义逆矩阵; rank{A}、tr(A)、span(A)、null{A}、vec(A)、vec-1(A)分别表示矩阵A的秩、迹、生成子空间、零空间、列矢量化和列矢量化的逆运算;⊗表示Kronecker积。

1 系统模型

考虑一多小区多用户FD-MIMO无线系统,基站工作在FD模式。在实际系统中,由于用户端FD技术的采用依赖于用户自身的硬件条件,因此,文中分别考虑两种情形:一种假设每个小区配置一组上行HD用户和一组下行HD用户,即图1(a)对应的多小区FD-BS-HD-User系统模型;另一种假设每个小区配置一组FD用户,即图1(b)对应的多小区FD-BS-FD-User系统模型。根据3GPP相关协议,基站间可通过回程链路进行信息交换,于是,文中假设基站端可完美重构干扰信号,即可直接将其他小区基站上行发送对基站下行接收所产生的干扰进行消除,因此,为了简化分析,文中暂不考虑基站间上下行干扰问题。

1.1 多小区FD-BS-HD-User系统模型

(1)

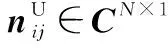
图1 多小区FD-MIMO系统模型Fig.1 Multi-cell FD-MIMO system model

每个基站不仅接收到本小区上行用户发送的期望信号,也能接收来自其他小区上行用户所发送的信号,此外,还能接收到SI信号,则小区a基站的上行接收信号可表示为

(2)

1.2 多小区FD-BS-FD-User系统模型

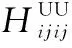
2 IA的可行性分析

2.1 FD-BS-HD-User模型

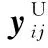
(3)

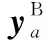
(4)

针对该模型,实现线性IA,对于小区i内下行用户j,必须满足以下条件

(5)

(6)

(7)

(8)

对于小区a上行用户b,必须满足以下条件

(9)

(10)

(11)

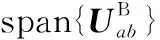
2.2 FD-BS-FD-User模型

(12)

(13)

按照第1.2节,将一FD用户等效为一上行用户和一下行用户,同时令K=KD=KU,d=dU=dD,则FD-BS-FD-User模型实现线性IA的条件等同于FD-BS-FD-User模型。

3 FD-MIMO系统中基于IA的干扰解决方案

在所提方案中,为了有效地对齐/消除相应的干扰,对于基站预编码矩阵和接收干扰抑制矩阵将分别采用两个级联矩阵来设计,即

(14)

(15)

(16)

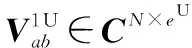
在该方案中,为了消除DIcIuI、DICI和UIcIuI、UICI,首先给出一种MTO线性IA算法,该算法又可分解为下行MTO IA和上行MTO IA,即通过设计基站预编码矩阵、下行用户外层接收干扰抑制矩阵和基站接收干扰抑制矩阵、上行用户外层预编码矩阵,达到消除上述干扰的目的。MTO线性IA算法同时适用于FD-BS-HD-User和FD-BS-FD-User两种系统模型,但对于FD-BS-FD-User模型,该算法只需基站确知上行CSI,而基站发送预编码和下行用户外层接收干扰抑制矩阵均可通过上行用户外层发送预编码和基站接收干扰抑制矩阵直接求得,因此,极大地减小了算法复杂度。在此基础上,为了抑制I-UuT-DuR,提出一种迭代IA算法。该算法以最小化I-UuT-DuR残留干扰为目标,构造一单边复合代价函数,进而通过格拉斯曼流形上的最速梯度下降法在上行用户端实现上行用户内层预编码矩阵的优化求解。该算法同样适用于FD-BS-HD-User和FD-BS-FD-User两种模型。

3.1 MTO线性IA算法

3.1.1 FD-BS-HD-User模型

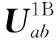
(17)

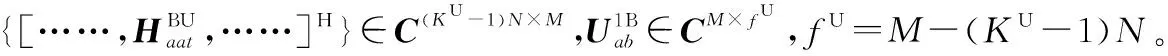
(18)

(19)

(20)

综上,通过式(18),完成基站内层接收干扰抑制矩阵的设计,从而将上行用户对其他小区所造成的UICI对齐到与该上行用户对应的干扰子空间内。将上述结果扩展到G个小区,式(18)可改写成式(21)。

(21)

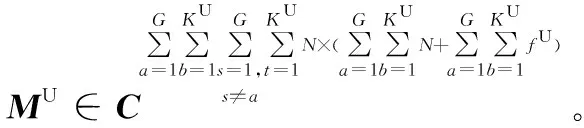
(22)

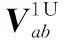
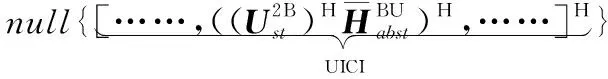
(23)

式中，s≠a。由式(21)和式(23)可知,

(24)

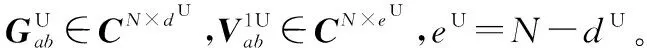
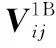
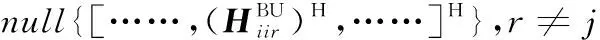
(25)

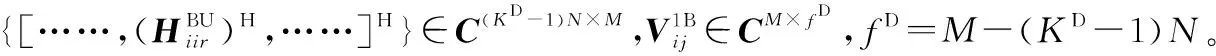
(26)

(27)

(28)

式(26)表示设计基站内层发送预编码矩阵,将下行用户所接收到的来自其他小区的DICI对齐到与该下行用户相对应的干扰子空间内。将上述结果扩展到G个小区,式(26)可改写成式(29)。

(29)

(30)

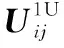
(31)

式中，i≠a,由式(29)和式(31)可推得

(32)

通过上述MTO 线性IA算法的设计过程,UIcIuI、UICI和DIcIuI、DICI均被完全消除,对应的IA可行性条件式(5)、式(6)、式(9)、式(10)均得到满足。

3.1.2 FD-BS-FD-User模型

按照第1.2节,将一FD用户等效为一上行用户和一下行用户。类似于FD-BS-HD-User系统模型,对于上行部分,通过上行MTO线性IA算法的设计以满足可行性条件式(5)、式(6),实现UIcIuI和UICI的消除。对于下行部分,通过下行MTO线性IA算法的设计,使其满足可行性条件式(9)、式(10),实现DIcIuI和DICI的消除。本小节中i,c,a,s∈{1,2,…,G},b,t,j,r∈{1,2,…,K}。

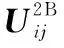
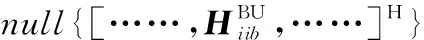
(33)

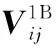
(34)

(35)

类似于FD-BS-HD-User系统模型,通过式(18)～式(20)设计FD用户所对应的基站的内层接收干扰抑制矩阵。对于G个小区,其结果类似于式(21),即

(36)

式中,i≠a。通过式(26)～式(28)设计FD用户所对应的基站的内层预编码矩阵。对于G个小区,同样地,可得到类似于式(29)的结果。

(37)

式中,c≠i。为保证式(37)和式(38)成立,则需满足:

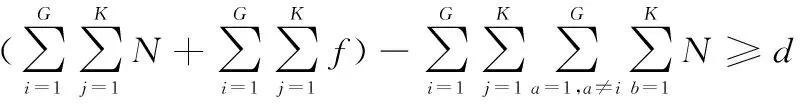
(38)

通过上述过程,式(36)所设计的基站端内层接收干扰抑制矩阵,将FD用户上行发送信号对其他小区所造成的(G-1)Kd维的UICI对齐到FD用户端的d维干扰子空间内;式(37)设计基站端内层发送预编码矩阵,将各FD用户接收到的来自其他小区的(G-1)Kd维的DICI被对齐到FD用户端的d维干扰子空间内。到此为止,基站端内层接收干扰抑制矩阵和内层预编码矩阵均完成设计,下面推导二者之间的关系。

(39)

从而对于G个小区,式(22)和式(31)中,对应元素满足如下关系，即

MD=MU

(40)

进而可推得

(41)

(42)

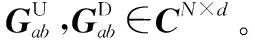
(43)

从而可推得

(44)

通过以上推导过程,对于 FD-BS-FD-User模型,利用MTO线性IA算法实现了UIcIuI、UICI和DIcIuI、DICI完全消除。由于FD-BS-FD-User模型的特殊性,所设计的基站端预编码矩阵和接收干扰抑制矩阵相等,用户端外层预编码矩阵和外层接收干扰抑制矩阵也相等。因此,在FD-BS-FD-User系统模型下,只需求得上行用户的外层发送预编码和基站的接收干扰抑制矩阵即可,此时,MTO线性IA算法仅需基站知道上行CSI,使得该方案在FD-BS-FD-User模型下的复杂度大幅度下降。

3.2 I-UuT-DuR抑制

通过第4.1节提出的MTO 线性IA算法,实现了UIcIuI、UICI和DIcIuI、DICI完全消除,在此基础上,通过设计上行用户内层预编码矩阵和下行用户内层接收干扰抑制矩阵,实现I-UuT-DuR的抑制。

在FD-MIMO系统中, I-UuT-DuR的消除只能在用户端完成,同时,在实际情况中,I-UuT-DuR又难以完全消除,因此,提出一种基于迭代IA的I-UuT-DuR抑制算法,以逼近式(7.3)的效果。所提的迭代IA算法同样适用于FD-BS-HD-User和FD-BS-FD-User两种模型,为了便于分析,在FD-BS-HD-User模型下,令dU=dD=d;而在FD-BS-FD-User模型中,如第1.2节所提,将FD用户从形式上分为一上行用户和一下行用户。在此基础上,基于迭代IA的I-UuT-DuR抑制算法设计过程如下。

(45)

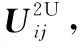
(46)

(47)

(48)

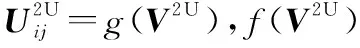
(49)

(50)

(51)

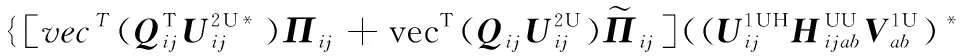
(52)

(53)

(55)

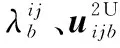
上行用户内层预编码变量沿格拉斯曼流形测地线移动的最速下降方向Zab可表示为

(56)

(57)

因此, 格拉斯曼最速下降方向表示为

(58)

综上所述,以抑制I-UuT-DuR为目标,基于格拉斯曼流形上的最速下降法迭代求解上行用户内层预编码矩阵的算法过程可用表1来表述。其中,对于最优步长的选取,参考已有研究本算法采用具有自适应功能的Armijo步长选择机制[17]。表1中qf{·}表示欧氏空间向对应的格拉斯曼流形上的投影计算。

表1 I-UuT-DuR抑制算法

4 仿真及性能分析

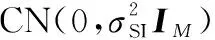
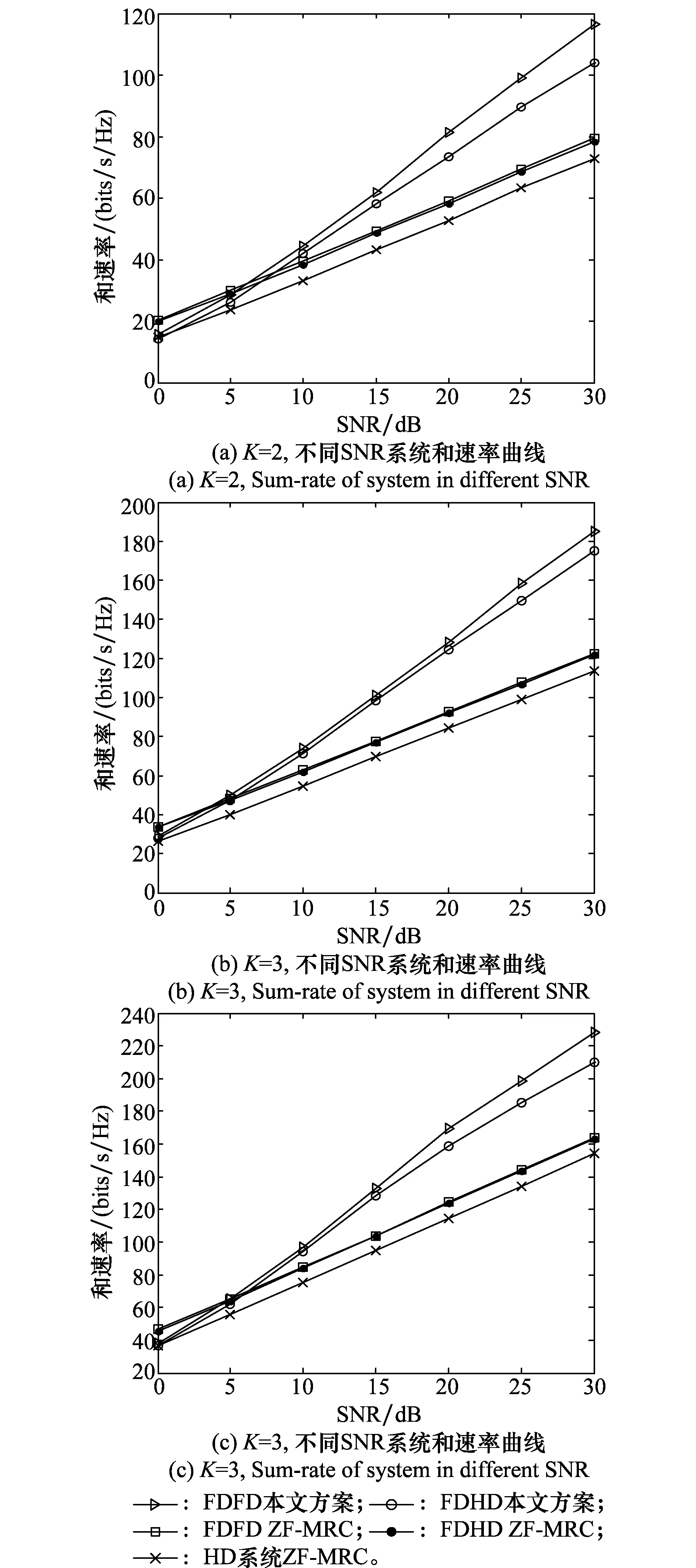
图2 不同SNR系统和速率曲线Fig.2 Sum-rate of system in different SNR

图2表明,SNR较低时,本文方案系统和速率低于ZF-MRC算法,这是由于在低SNR情况下,本文方案在进行空域IA的同时,削弱了期望信号的功率,而ZF-MRC算法则致力于最大化期望信号;SNR较高时,本文方案性能明显优于ZF-MRC算法,且随SNR增加,性能优势更加突出,这是由于随SNR的增加,系统干扰将会变得越来越严重,此时,系统性能主要受制于系统干扰,而本文方案恰好能有效地抑制系统干扰。

同时,在图2(a)～图2(c)中,用户端分别配置了5、7、8根天线,而根据前述方案分析,本文分别采用3、5、6根天线实现了I-UuT-DuR的抑制,而ZF-MRC算法中并没有对I-UuT-DuR进行相应的处理,因此,在同等天线配置条件下,本文方案可带来可观的和速率增益。进一步,对于ZF-MRC算法,若直接采用ZF算法消除I-UuT-DuR,对于图2(a)～图2(c)中3种配置,用户端则至少需要6、9、12根天线,虽然其可实现I-UuT-DuR的完全消除,但所需天线数目明显多于本文方案,造成天线资源的浪费。

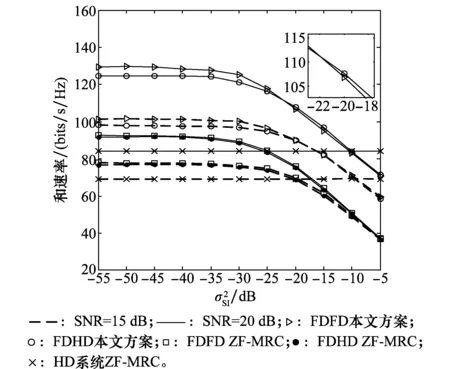
图3 不同下系统和速率曲线Fig.3 Sum-rate of system in different SI index

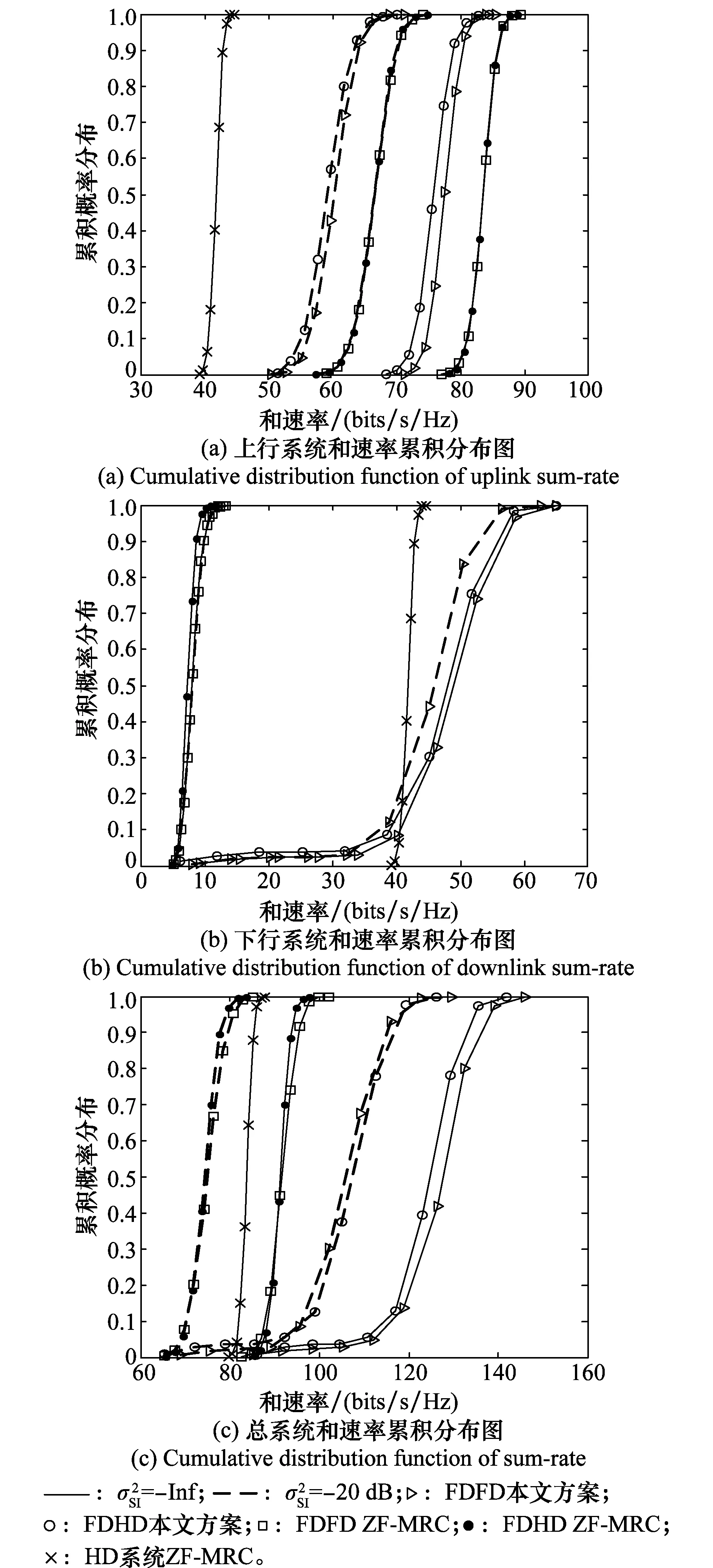
图4 系统和速率累积分布图Fig.4 Cumulative distribution function of sum-rate

观察图4(b),对于下行和速率性能,本文方案以80%以上的概率优于HD系统ZF-MRC算法,而FD系统ZF-MRC算法远低于HD系统ZF-MRC算法,这是由于本文方案和FD-BS-HD-User系统ZF-MRC算法可利用的传输资源均为HD系统ZF-MRC算法的两倍,但FD-BS-HD-User系统ZF-MRC算法受到严重的I-UuT-DuR,而本文方案有效地抑制了I-UuT-DuR。

图4(c)表明,本文方案总和速率性能明显优于ZF-MRC算法。这说明:本文所提方案充分利用FD-MIMO系统中的传输资源,有效地解决了FD-MIMO系统中复杂的干扰问题,因而使得系统和速率得到大幅度提升。

5 结 论

FD-MIMO技术尽管具有成倍提升系统频谱效率的潜力,但由此引起的复杂干扰问题成为制约其商业化应用的关键因素。文中针对多小区多用户FD-MIMO系统,在分析FD-MIMO系统IA可行性条件的基础上,结合IA,提出一种适用于FD-MIMO系统的干扰解决方案,从而为消除FD-MIMO系统中繁杂干扰提供了新思路。该方案同时适用于FD-BS-FD-User和 FD-BS-HD-User两种模型下的多小区FD-MIMO系统。

该方案由MTO线性IA算法和基于格拉斯曼流形上的迭代IA算法组成,其中MTO线性IA算法主要用于消除UIcIuI、UICI及DIcIuI和DICI;而基于格拉斯曼流形上的迭代IA算法主要用于抑制I-UuT-DuR。理论分析和数值仿真表明,与传统算法相比,本文所提算法有效地解决了多小区FD-MIMO系统中干扰问题,相对HD-MIMO系统,系统和速率得到明显提升。

参考文献：

[1] MASMOUDI A, LENGOC T. A maximum-likelihood channel estimator for self-interference cancelation in full-duplex systems[J].IEEE Trans.on Vehicular Technology,2016,65(7):5122-5132.

[2] SABHARWAL A, SCHNITER P, GUO D. In-band full-duplex wireless: challenges and opportunities[J]. IEEE Journal on Selected Areas in Communications,2014,32(9):1637-1652.

[3] NGUYEN D, TRAN L N, PIRINEN P. Precoding for full duplex multiuser MIMO systems: spectral and energy efficiency maximization[J]. IEEE Trans.on Signal Processing, 2013, 61(16): 4038-4050.

[4] BERHANE T M, MENG W X, CHEN L, et al. SLNR-based precoding for single cell full-duplex MU-MIMO systems[J]. IEEE Trans.on Vehicular Technology, 2017,66(99):7877-7887.

[5] PANAHI F H, OHTSUKI T, JIANG W. Joint interference alignment and power allocation for multi-user MIMO interference channels under perfect and imperfect CSI[J]. IEEE Trans.on Green Communications and Networking, 2017,1(2):131-144.

[6] GOMADAM K, CADAMBE V R, JAFAR S A. A distributed numerical approach to interference alignment and applications to wireless interference networks[J]. IEEE Trans.on Information Theory, 2011, 57(6): 3309-3322.

[7] TANG J, LAMBOTHARAN S. Interference alignment techniques for MIMO multi-cell interfering broadcast channels[J]. IEEE Trans.on Communications, 2013, 61(1): 164-175.

[8] KIM K, JEON S W, DONG K K. The feasibility of interference alignment for full-duplex MIMO cellular networks[J]. IEEE Communications Letters, 2015, 19(9):1500-1503.

[9] KHOJASTEPOUR M A A, SUNDARESAN K, RANGARAJAN S. Scaling wireless full-duplex in multi-cell networks[C]∥Proc.of the IEEE Conference on Computer Communications, 2015:1751-1759.

[10] BAI J, DIGGAVI S, SABHARWAL A. On degrees-of-freedom of multi-user MIMO full-duplex network[C]∥Proc.of the IEEE International Symposium on Information Theory,2015:864-868.

[11] JEON S W, CHAE S H, LIM S H. Degrees of freedom of full-duplex multiantenna cellular networks[C]∥Proc.of the IEEE International Symposium on Information Theory,2015:869-873.

[12] YANG M, JEON S W, KIM D K. Degrees of freedom of full-duplex cellular networks with reconfigurable antennas at base station[J]. IEEE Trans.on Wireless Communications, 2017, 16(4): 2314-2326.

[13] SHIN W, LIM J B, CHOI H H, et al. Cyclic interference alignment for full-duplex multi-antenna cellular networks[J]. IEEE Trans.on Communications, 2017,65(6):2657-2671.

[14] MANTON J H. Optimization algorithms exploiting unitary constraints[J].IEEE Trans.on Signal Processing,2002,50(3):635-650.

[15] NGO T, SAAD Y. Scaled gradients on grassmann manifolds for matrix completion[C]∥Proc.of the Advances in Neural Information Processing Systems, 2012: 1412-1420.

[16] HJØRUNGNES A. Complex-valued matrix derivatives: with applications in signal processing and communications[M]. New York: Cambridge University Press, 2011.

[17] BONNANS J F, GILBERT J C, LEMARÉCHAL C, et al. Numerical optimization： theoretical and practical aspects[M].New York: Springer Science & Business Media,2013.