基于BP神经网络多类分类的湍流目标探测

张 强, 肖 刚, 蓝屹群

(1. 上海交通大学航空航天学院, 上海 200240; 2. 上海民航职业技术学院航空维修系, 上海 200232)

0 引 言

机载气象雷达(简称为WXR)作为飞机环境监视系统的子系统,通过探测飞行航路前方一定扇形区域内的天气情况,可以在恶劣气象条件下保障飞机和机上人员的安全。其中,气象湍流是影响飞机飞行安全的重要因素之一,严重的湍流不仅会使飞机颠簸,影响飞机结构安全,更会影响机上人员的安全。2017年6月18日凌晨,从法国巴黎飞往中国昆明的东航MU774航班在飞行途中突遇强烈湍流,持续10多分钟,造成28人受伤,其中4人重伤。为了避免这样的安全事故发生,需要通过WXR进行有效的湍流探测或预警。

湍流是在一定时间和空间范围内风速的随机波动,波动的幅度越大,雷达回波信号多普勒谱宽越宽,湍流强度越大。引发湍流的原因有很多,包括气压变化、雷暴、急流等,甚至在晴朗的天空也会出现湍流。其中,夹杂着雨滴的为湿性湍流,不夹杂着雨滴的为晴空湍流,目前多数的湍流检测算法只能对湿性湍流进行有效的探测,而无法有效探测晴空湍流[1-3]。

通过确定的物理原理来探测湍流的方法称为非参数化方法[4-5]。文献[6]通过脉冲对(pulse-pair,PP)方法估计气象雷达回波的平均多普勒频率和多普勒谱宽来探测湍流强度,但是该方法只适用于雷达回波信噪比(signal-to-noise ratio,SNR)较高的情况。文献[1,7]利用快速傅里叶变换(fast Fourier transform,FFT)方法提取了回波数据中风速和谱宽等参数,该方法在考虑地杂波的情况下依然可以有效地检测到湍流信号,但是在回波数据长度较短的条件下,谱估计性能变差。通过分析回波信号和气象目标运动特性之间的参数化关系,提出参数化模型来探测湍流称为参数化方法[8-9]。文献[3,10-12]提出基于对数似然比的湍流探测方法,通过使回波数据拟合所提出的概率模型来检测湍流,该方法假设湍流回波功率谱服从单高斯谱分布,但是文献[13]通过对实际数据的研究发现有些情况WXR回波数据更加符合多个高斯谱叠加的模型。因此文献[2,14]提出通过非线性最小二乘的方法,使回波数据拟合所提出的自相关序列模型来估计谱宽等参数,该方法综合考虑了单高斯谱和多高斯谱的情况,但是该方法计算复杂性较高。本文提出基于神经网络的湍流目标探测方法,利用神经网络通过调整节点之间权值和阈值可以拟合任意非线性模型的特点[15],采用一类对多类(one-VS-all)的分类方法,直接对湍流回波信号进行等级分类得到湍流强度大小或有无。最后通过仿真实验分析证明该方法的有效性。

1 湍流回波模型

根据文献[16],湍流区域的雷达回波信号是一个相关随机过程,同一气象目标的相邻2个脉冲回波之间的相关系数为

(1)

式中,Ts为脉冲重复周期;λ为波长;σv为气象目标的多普勒速度谱谱宽,是湍流的主要参数之一,用来判别湍流强度的大小。速度谱宽越宽,湍流强度越大,速度谱宽与湍流强度之间的对应关系如表1所示[10]。

表1 湍流强度分类

假设时刻t=ti时回波信号为x(ti),则

x(ti)=si+ni=

S(ti)cos(ω0ti+φ)+ni, 1≤i≤N

(2)

式中,si为气象目标回波信号;ni为加性高斯白噪声;ω0为载波频率;φ为相位;N为回波数据长度,一般取8、16、32等。设其幅值为xi,则

(3)

式中,n1i、n2i为不相关高斯白噪声;A(ti)、B(ti)为回波信号幅值的正交分量。则x1、x2、…、xN组成长度为N的雷达回波幅值序列,该幅值序列是服从瑞利分布和指数相关性的马尔可夫随机过程[10]，即

(4)

式中,φi为均匀分布在0～2π的随机相位;r为相邻回波信号幅值的指数型相关系数;ηi为服从瑞利分布的随机序列,该瑞利分布参数为

(5)

式中,kR是与雷达特性有关的值。

2 基于BP神经网络的湍流探测

本文所提出的基于反向传播(back propagation,BP)神经网络的湍流探测算法利用神经网络one-Vs-all的多类分类功能对湍流强度进行分类从而达到探测湍流的目的。由式(1)～式(5)可以看出,雷达回波幅值序列与湍流强度等级(即速度谱宽σv值)有对应关系,根据不同的σv值,可以产生与其相对应的若干组某一气象目标一定长度的回波幅值序列。则每一组回波幅值序列与其对应的湍流强度等级组成一个训练样本:幅值序列作为神经网络训练集输入数据,强度等级作为训练集输出数据。通过对大量仿真数据的学习,神经网络将可以直接对雷达回波信号进行分类处理,根据分类结果判定湍流的强弱或有无。

考虑到神经网络分类功能对输出数据的要求,根据表1将湍流强度分为4个等级,如表2所示。速度谱宽σv在0～1.5 m/s之间设为等级1,在1.5～3.0 m/s之间设为等级2,在3～4.5 m/s之间设为等级3,在4.5 m/s以上设为等级4。

表2 湍流强度四等级分类

若只考虑判断湍流存在与否,而不用将湍流强度详细分为4个等级时,即当σV>1.5 m/s,湍流等级为2(轻微)、3(中度)、4(强)时,设为湍流存在;当σV<1.5 m/s,湍流等级为1(可忽略)时,设为湍流不存在。即把湍流4等级分类变成二等级分类(判定湍流有无)时,分类表如表3所示。

表3 湍流强度二等级分类

神经网络解决多类分类问题的本质是把原分类问题分解为one-vs-all的分类问题,即输出y为一个向量

(6)

对应的y∈{1,2,3,…n}中的某个值。简单地,当输出y=[1,0]T时,对应y=1;当输出y=[0,1]T时,对应y=2。在本文中输出y与湍流四等级强度对应关系如表4所示。

表4 四等级分类对应的输出y值

即针对一组输入数据(雷达回波信号幅值序列),当神经网络输出结果为[1,0,0,0]T时,判定湍流等级为1,强度为可忽略;当输出结果为[0,1,0,0]T时,判定湍流等级为2,强度为轻微级;当输出结果为[0,0,1,0]T时,判定湍流等级为3,强度为中度级;当输出结果为[0,0,0,1]T时,判定湍流等级为4,强度为强级。输出y与湍流有无对应关系如表5所示。

表5 二等级分类对应的输出y值

即针对一组输入数据(雷达回波信号幅值序列),当神经网络输出结果为[1,0]T时,判定湍流不存在;当输出结果为[0,1]T时,判定湍流存在。

3 仿真分析

3.1 仿真数据准备

本文所采用的WXR工作波长λ为0.03 m,脉冲重复周期Ts为0.001 s,参数kR约为1 W·s2/m2。针对不同的σV值,分别生成长度为8、16、32的回波幅值序列,与其对应的强度等级组成神经网络训练集和测试集。其中训练集样本量为2 800组,测试集样本量为1 200组,训练集和测试集内随机分布所有强度等级的湍流幅值序列。

3.2 仿真结果及分析

图1～图3分别表示当SNR为10 dB,序列长度分别为8、16、32时,取不同隐藏层单元数对应的四等级分类训练准确率和测试准确率。

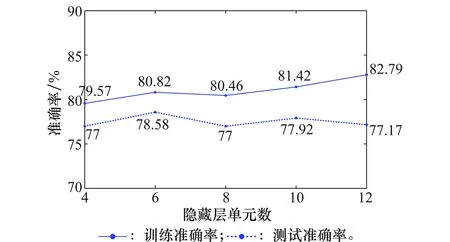
图1 序列长度为8时的训练与测试准确率(SNR=10 dB)Fig.1 Training and testing accuracy when sequence length equals 8 (SNR=10 dB)

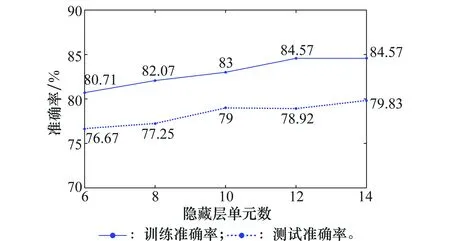
图2 序列长度为16时的训练与测试准确率(SNR=10 dB)Fig.2 Training and testing accuracy when sequence lengthequals 16 (SNR=10 dB)

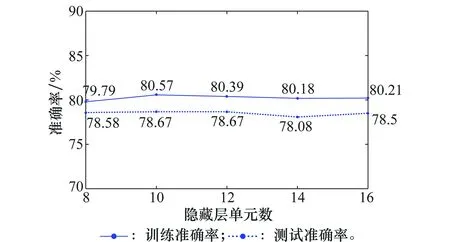
图3 序列长度为32时的训练与测试准确率(SNR=10 dB)Fig.3 Training and testing accuracy when sequence length equals 32 (SNR=10 dB)

图4～图6分别表示当SNR为20 dB,序列长度分别为8、16、32时,取不同隐藏层单元数对应的四等级分类训练准确率和测试准确率。

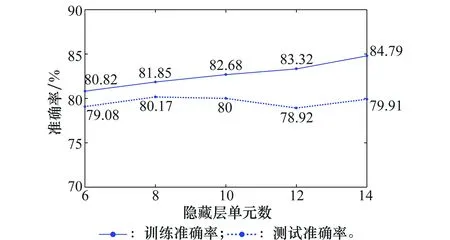
图5 序列长度为16时的训练与测试准确率(SNR=20 dB)Fig.5 Training and testing accuracy when sequence lengthequals 16 (SNR=20 dB)

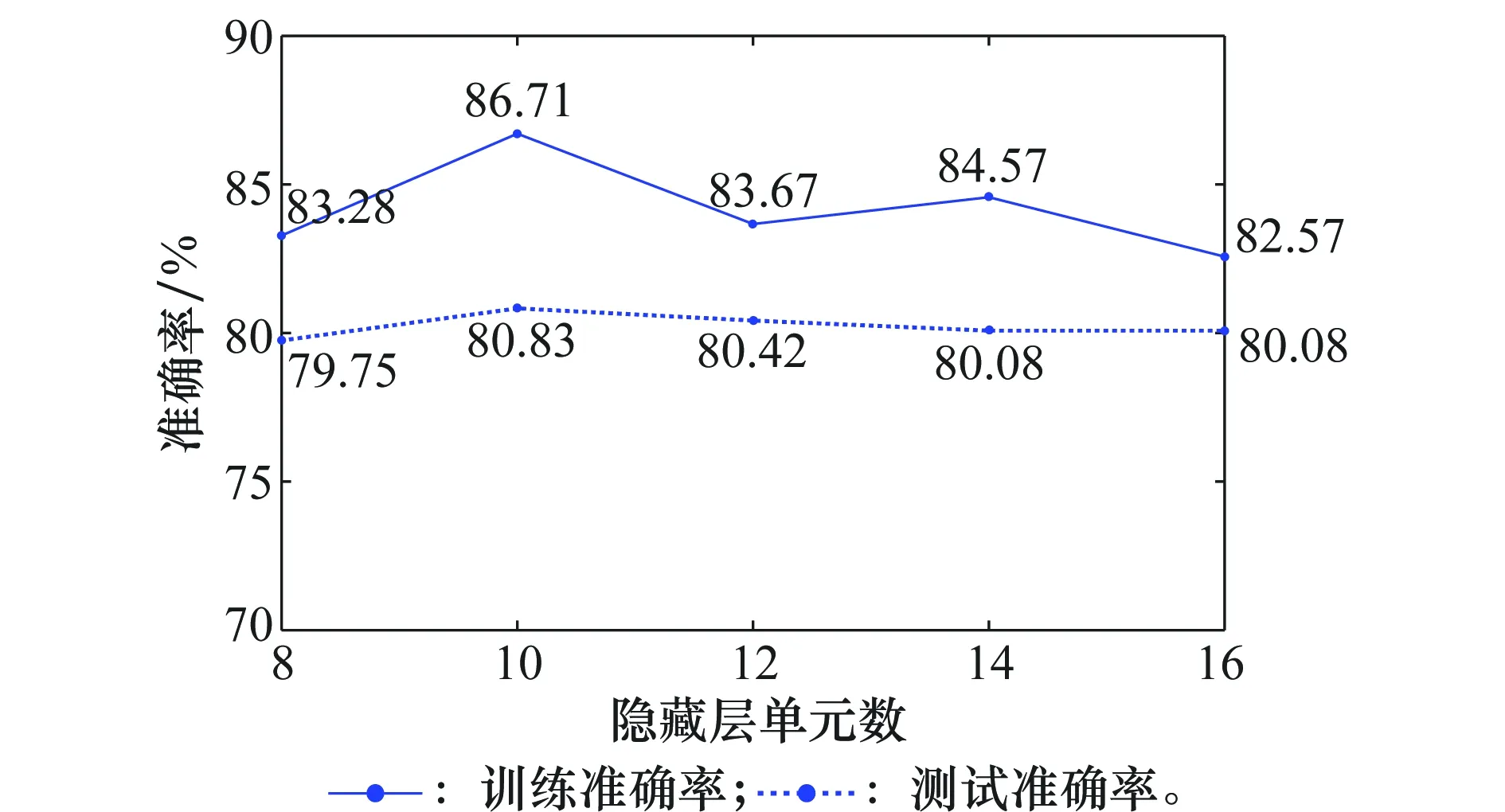
图6 序列长度为32时的训练与测试准确率(SNR=20 dB)Fig.6 Training and testing accuracy when sequence lengthequals 32 (SNR=20 dB)

图7表示SNR为10 dB和20 dB,序列长度分别为8、16、32时,四等级分类的神经网络平均测试准确率。

图7 四等级分类时平均测试准确率Fig.7 Average testing accuracy of four levels classification

由图7可知,当SNR为10 dB,序列长度分别为8、16、32时,该算法分别有77.45%、78.25%、78.62%的概率正确地将湍流强度分为4个等级,从而探测出湍流的强度值;当SNR为20 dB时,该算法分别有78.73%、79.53%、80.38% 的概率正确地将湍流强度分为4个等级,从而探测出湍流的强度值。

图8表示SNR为10 dB和20 dB,序列长度分别为8、16、32时,二等级分类的神经网络平均测试准确率。由图8可知,当SNR为10 dB,序列长度分别为8、16、32时,该算法分别有96.83%、97.42%、97.87%的概率正确地将湍流强度分为2个等级,从而探测出湍流的有无;当SNR为20 dB时,该算法分别有97.4%、98.58%、98.72% 的概率正确地将湍流强度分为2个等级,从而探测出湍流的有无。与识别出4个等级的湍流强度相比,当只需要探测出湍流是否存在时,所提出的方法准确率大大提高。

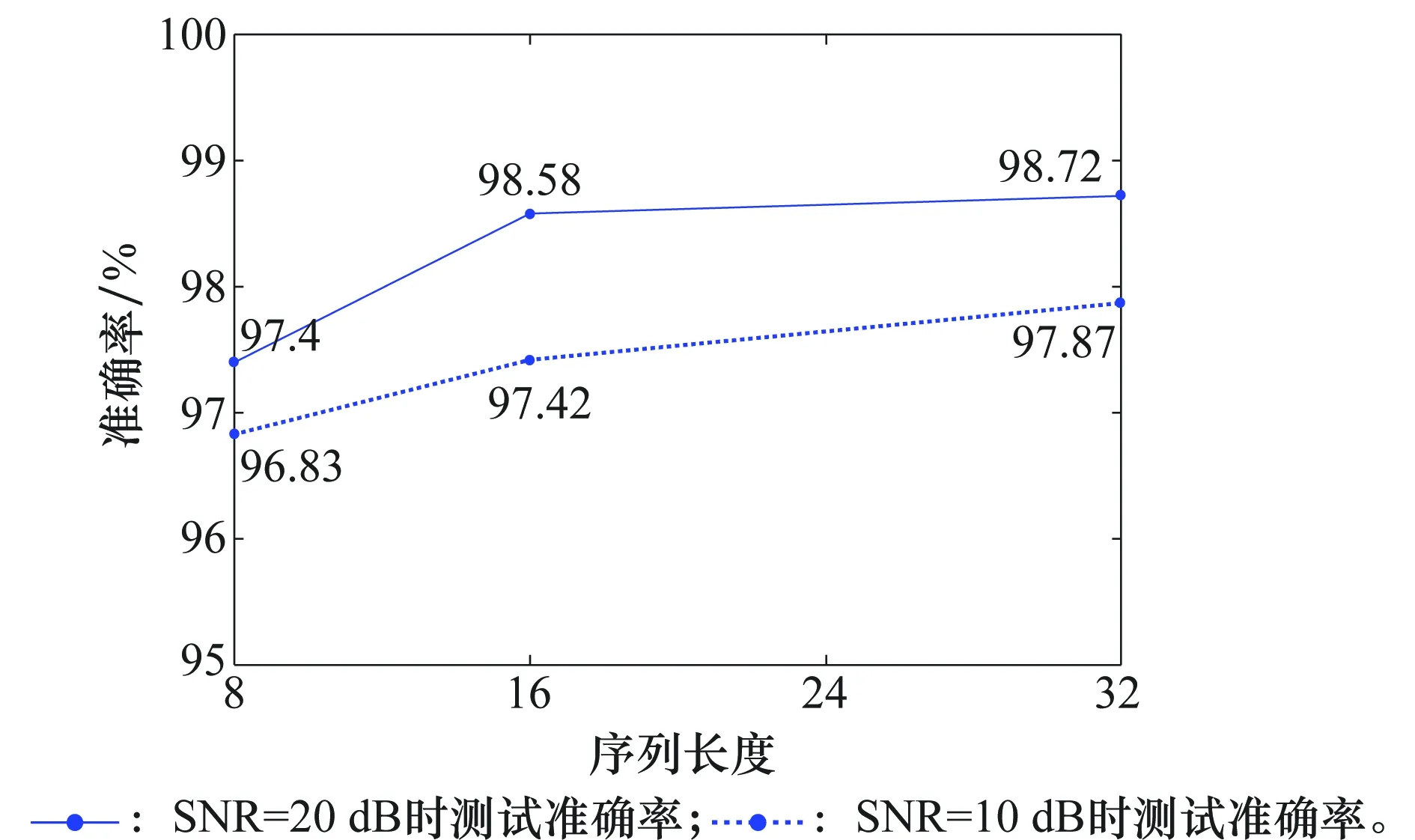
图8 二等级分类时平均测试准确率Fig.8 Average testing accuracy of two levels classification

由图7、图8分析可知,当SNR一定时,幅值序列长度越长,平均测试准确率越高,因为序列长度越长时,所包含的关于湍流强度的信息越多;当序列长度一定时,SNR值较大的情况下,平均测试准确率较高,因为SNR值较大时,更容易从回波幅值序列中提取关于湍流强度的信息。该算法的实验结果符合实际情况且性能良好,因此本文所提出的基于反向传播神经网络多类分类方法的湍流探测算法可有效地探测湍流目标。

4 结 论

本文提出了基于反向传播神经网络多类分类的湍流目标探测方法,利用神经网络多类分类功能直接对湍流幅值序列进行分类,识别出湍流强度的4个等级从而探测湍流的强度大小,或探测湍流是否存在。实验结果表明,所提出的方法在进行湍流4个等级分类时有较高的准确率,且当只需进行湍流2个等级(有或无)的分类时,准确率更进一步提高。本文所提出的方法与传统非参数化和参数化方法相比,最大的优点是不需要借助经验公式和各种模型及复杂的运算,仅通过神经网络自身的学习就可以快速有效地探测出湍流强度大小或有无。

在实际的实验过程中,随着隐藏层的增加,出现了严重的过拟合现象,考虑到现阶段本文只观察幅值序列长度和SNR对最终结果的影响,对不同程度的过拟合现象通过调整正则化参数取得最优值并做平均计算。在下一步的研究中,将使用实际的WXR数据进行神经网络的训练,以设计更加符合湍流探测的神经网络结构并选择适当的算法以自适应地解决在训练过程中出现的过拟合问题,进一步提高测试准确率。

参考文献：

[1] 刘小洋,李勇,程宇峰. 机载气象雷达湍流信号的仿真分析[J].系统工程与电子技术, 2012, 34(5):920-924.

LIU X Y, LI Y, CHENG Y F. Simulation and analysis of turbulence signals in airborne pulse Doppler radar[J]. Systems Engineering and Electronics, 2012,34(5):920-924.

[2] 卢晓光,吴仁彪. 基于非线性最小二乘的机载气象雷达回波谱矩估计方法[J].系统工程与电子技术,2014,36(3):447-452.

LU X G, WU R B. Nonlinear least-squares spectral moment estimation algorithm for airborne weather radar[J].Systems Engineering and Electronics, 2014,36(3): 447-452.

[3] 刘小洋. 基于对数似然比的湍流目标检测[J].智能计算机与应用,2014,4(4):5-8.

LIU X Y. Turbulence target detection based on the logarithmic likelihood ratio[J].Intelligent Computer and Application, 2014, 4(4):5-8.

[4] DIAS J M B, LEITAO J M N. Nonparametric estimation of mean Doppler and spectral width[J].IEEE Trans.on Geoscience and Remote Sensing, 2000,38(1):271-282.

[5] YANOVSKY F J, RUSSCHENBERG H W J, UNAL C M H. Retrieval of information about turbulence in rain by using Doppler-polarimetric radar[J]. IEEE Trans. On Microwave Theory and Techniques, 2005,53(2):444-450.

[6] SAMAN S A. Efficient frequency estimation using the pulse-pair method at various lags[J]. IEEE Trans.on Communication.2006,54(9):1542-1546.

[7] 于莹洁,李勇.一种机载气象雷达湍流信号的检测方法及仿真[J].西北工业大学学报,2015,33(1):159-164.

YU Y J, LI Y. An airborne weather radar turbulence signal detection method and simulation[J].Journal of Northwestern Poly-technical University, 2015,33(1):159-164.

[8] BOYER E, LARZABAL P, ADNET C, et al. Parametric spectral moments estimation for wind profiling radar[J]. IEEE Trans.on Geoscience and Remote Sensing,2003,41(8):1859-1868.

[9] FOLL G L, LARZABAL P, CLERGEOT H, et al. A new parametric approach for wind profiling weather radar[J]. Radio Science, 1997,32(4):1391-1408.

[10] YANOVSKY F J, PROKOPENKO I G, LIGTHART L P. New adaptive algorithm for radar turbulence detection in clouds and precipitation[C]∥Proc.of the Geoscience and Remote Sensing Symposium, 2000: 3145-3147.

[11] LIGTHART L P, YANOVSKY F J, PROKOPENKO I G. Adaptive algorithms for radar detection of turbulent zones in clouds and precipitation[J].IEEE Trans.on Aerospace and Electronic Systems, 2003,39(1):357-367.

[12] PROKOPENKO I G, LIGTHART L P, YANOVSKY F J. Adaptive algorithms for weather radar[C]∥Proc.of the European Radar Conference, 2004: 329-332

[13] YU T Y, RONDINEL R R, PALME R D. Investigation of non-Gaussian Doppler spectra observed by weather radar in a tornadic supercell[J].Journal of Atmospheric and Oceanic Technology, 2009, 26(3):444-461.

[14] BESSON O, STOCIA P. Nonlinear least-squares approach to frequency estimation and detection for sinusoidal signals with arbitrary envelope[J]. Digital Signal Processing, 1999,9(1):45-56.

[15] RUMELHART D E, HITON G E, WILLIAMS R J. Learning representations by backpropagation errors[J]. Nature, 1986, 323(9):533-536.

[16] DOVIAK R J, ZRINIC D S. Doppler radar and weather observations[M].New York: Academic Press,1993.