考虑非最小相位特性的高超声速飞行器轨迹跟踪控制

晁 涛, 王雨潇, 王松艳, 杨 明

(哈尔滨工业大学控制与仿真中心, 黑龙江 哈尔滨 150001)

0 引 言

与传统飞行器相比,高超声速飞行器飞行速度高,突防能力强,受到各军事大国的普遍关注[1]。由于高超声速飞行器极大的飞行速度和复杂的飞行环境,导致其动力学具有强耦合、强非线性、强不确定性等特点。此外由于吸气式高超声速飞行器的“飞推一体化”设计构型,在纵向通道内飞行器呈现非最小相位特性[2]。这些特点给它的控制律设计带来很大困难。

目前有关吸气式高超声速飞行器的六自由度建模和控制研究成果极少,绝大多数的控制方法研究都是针对飞行器的纵向三自由度模型。一些如线性二次型调节器(linear quadratic regulator,LQR)等简单的线性控制方法建立在线性化的飞行器模型基础上[3-5]。动态逆和反步法等控制方法直接应用在非线性模型上[6-10],但依赖于精确数学模型的方法会存在系统鲁棒性问题,反步设计会产生“微分爆炸”问题[7]。考虑到反步控制存在“复杂度爆炸”问题,文献[7-8]将动态面控制引入到反步控制中,文献[8]利用神经网络自适应估计系统的不确定性,最后证明闭环系统跟踪误差是一致有界的。文献[9]利用线性变参数模型(linear parameter-varying,LPV),设计自适应控制律实现闭环系统跟踪。

而对于非最小相位系统,系统的相对阶数小于系统的状态数,传统的反步法设计会使系统产生不稳定内动态,无法实现系统的全局稳定。输出重定义方法通过定义一个新的系统输出使其变为一个最小相位系统,从而使系统可以用常规控制方法解决[11]。但输出重定义方法存在其特有的应用难题,一方面是目前不存在通用的方法来寻找这样一个新输出;另一方面输出重定义方法也会给系统带来新输入不确定性。

对于飞行器系统,其非最小相位特性给控制系统设计带来了不小的难题。文献[12]分析了欠驱动再入飞行器的非最小相位特性,进一步地,针对此飞行器姿控系统的非最小相位问题,将系统转化为一种正则形式,给出系统非最小相位特性的定量判据。文献[13]在此基础上,加入了一种二阶滑模控制方法,成功地镇定了系统的不稳定内动态。这也给一般的非最小相位问题提供了解决思路。

对于尾控式飞行器,升降舵的改变会同时对飞行器的升力和俯仰力矩产生影响。在反步法设计过程中,如果不忽略尾翼对升力的影响,系统存在二阶的不稳定内动态,系统的纵向通道存在非最小相位特性,这给控制律设计带来了麻烦。在一些方法中,飞行器被人为加入鸭翼操纵面,利用鸭翼来抵消尾翼对升力产生的影响,系统因此转变为最小相位系统[14-15],从而完成控制器设计。然而,鸭翼已被证明会产生更严重的气动热问题,无法直接加入到飞行器的执行机构中。一些文献在没有鸭翼的情况下针对非最小相位动力学设计控制律[16-18]。文献[16]在反步法的设计中忽略了尾翼对系统升力的影响,从而使系统相对阶与系统阶数相等,消除了内动态,最后通过积分反馈来消除由于忽略尾翼影响造成的跟踪静差。文献[17]将高增益反馈与饱和低增益反馈相结合,迫使系统表现出二时间尺度特性。然后利用非线性系统的小增益定理,证明闭环系统稳定。文献[18]通过输出重定义方法来解决非最小相位问题。选取俯仰角偏差作为新的输出,此时内动态弹道倾角为稳定的,系统是最小相位的。而这同时为系统带来了输入不确定性,文中加入积分控制来保证系统无静差。通过利用非线性系统的小增益定理和自适应控制,使得闭环系统的跟踪误差是渐近稳定的。

针对带有非最小相位特性的吸气式高超声速飞行器控制问题,借鉴飞行器姿控系统非最小相位问题中所应用的转换正则形式方法,设计了一种飞行器纵向输出跟踪控制方法。对于不具有非最小相位特性的速度子系统,运用动态逆控制技术设计了状态反馈控制器;针对具有非最小相位特性的高度子系统,首先选择合理的局部微分同胚,将纵向俯仰通道模型转换为正则形式,得到内动态。通过对内动态进行稳定性分析并给出系统非最小相位特性的判据。最后基于Lyapunov方程和最小范数控制策略设计了纵向通道控制器,控制器有效地抑制了系统内动态,达到了良好的控制效果。

1 模型描述

一般的吸气式高超声速飞行器纵向模型描述[19]为

(1)

系统拥有4个状态[V,γ,θ,Q]T和2个控制量[Φ,δe]T。模型参数及适用范围来源于文献[20],推力T、阻力D、升力L、俯仰力矩M拟合如式(2)所示,且各变量的含义及模型适用范围如表1所示。

(2)

2 非最小相位特性判定

2.1 系统非最小相位特性分析

针对高度子系统

(3)

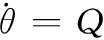
(4)

(5)

对于高度子系统,系统输出为弹道倾角γ,控制量为升降舵δe。从式(3)不难得到,系统相对阶为1,小于系统阶数3,所以系统存在二阶内动态。

通过对系统的零动态仿真分析,二阶零动态均呈发散趋势,在不稳定零动态的影响下,系统的外部输出也会迅速超出可行范围,系统具有非最小相位特性。

2.2 系统非最小相位特性判据

针对高度子系统,存在一个局部微分同胚，即

Φ(x):x→(ζ,η)

(6)

将式(3)～式(5)转化为正则形式。转化后的正则形式可表示为

(7)

其中,外动态

(8)

内动态

(9)

定理1若飞行器系统(1)参数满足条件

(10)

则此飞行器的高度子系统具有非最小相位特性。

(11)

(12)

式中

(13)

(14)

对内动态η2求取二阶导数,得到

(15)

若系统满足式(10),则

(16)

则方程(15)存在正根,内动态η不稳定,系统具有非最小相位特性。

证毕

上述定理为飞行器模型的非最小相位特性分析提供了关于气动参数的定量判据。

从实际飞行器气动特性的物理意义上来讲,气动舵在产生升力的同时,会产生俯仰力矩,从而会改变飞行器的攻角,这部分攻角所产生的升力与气动舵产生的升力方向相反。而式(10)成立,代表后者由于攻角产生的升力要大于气动舵本身产生的升力。在一般的飞行器中,纵向通道采用尾翼控制,高度子系统基本都会具有非最小相位特性。

3 控制器设计

3.1 速度子系统

对于速度子系统

(17)

(18)

式中

(21)

设计动态逆控制器

ϑ1]

(22)

得到

(23)

根据式(23)可以看出,所设计动态逆控制器可以保证系统实现速度通道的渐近跟踪。

3.2 高度子系统

(24)

首先设计动态逆控制器,令

(25)

得到

(26)

式中,u为虚拟控制量。

将式(26)代入正则形式的系统方程(7),系统可以写为

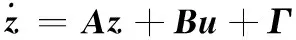
(27)

式中

z=[ζη1η2]T

(28)

(29)

B=[1 0 0]T

(30)

Γ=[0Γ1Γ2]T

(31)

为了实现对z的线性反馈、镇定内动态,令

u=u′-Kz

(32)

选取合适的增益矩阵K=[k1k2k3],使得A′=A-BK为Hurwitz矩阵。

此时系统方程变为

(33)

对任意给定的对称正定矩阵Q,存在P使得Lyapunov方程成立，即

A′P+PA′=-Q

(34)

选取Lyapunov函数

V=zTPz

(35)

对V求导得到

(36)

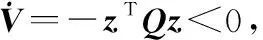
基于最小范数控制策略,有

(37)

则伪控制量

(38)

根据式(25)、式(38)可得原系统的弹道倾角输出跟踪控制器为

(39)

从控制器设计过程来看,在动态逆控制器的基础上加入了z的反馈项,成功地解决了单一动态逆控制器会使内动态发散的问题。

值得一提的是,在其他一些解决飞行器非最小相位问题的方法中,角度积分项反馈经常会被加入到控制器中,解决由于忽略模型项造成的稳态误差等问题。而本文所提出方法的内动态η2经计算得到的单位是rad×s2,是关于角度二次型的积分项,与其他方法得到了相似的结果。所以,角度积分项反馈在处理非最小相位问题的方法中起到的作用还值得深入研究。

4 仿真分析

为了验证算法的有效性,给出了一组巡航状态下的吸气式高超声速飞行器仿真示例。考虑吸气式高超声速飞行器纵向模型,表2给出了模型参数适用范围内的一组飞行器的初始条件。

表2 飞行器初始条件

首先验证高超声速飞行器高度子系统是否具有非最小相位特性,即

(40)

根据计算结果可以判断此高超声速飞行器的高度控制子系统为非最小相位系统。

设置飞行器纵向跟踪指令为

Vc=8 860 ft/s

(41)

γc=0

(42)

首先采用常用的思路,忽略模型中升降舵对升力的影响,使模型变为最小相位系统,这样可以采用标准的反步法来设计控制器。燃油节流率和升降舵可以分别实现对速度V和弹道倾角γ的控制,仿真结果如图1所示。

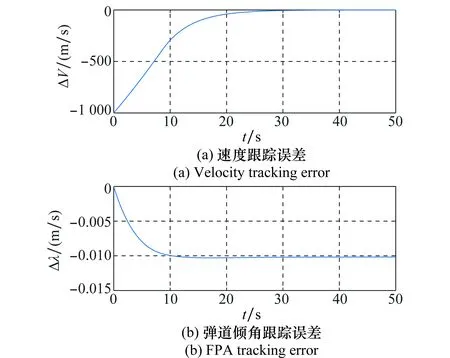
图1 反步法跟踪误差Fig.1 Tracking errors of back-stepping method

从图1可以看出,飞行器在25 s左右达到稳定跟踪,由于在弹道倾角方程中忽略了舵偏角对其的影响,其中弹道倾角γ存在稳态误差,约为0.01 rad。

下面采用文中所设计控制器来进行仿真。根据上文控制器设计原则选取控制器参数,令式(32)中增益向量为

K=[15,-1,1]T

(43)

仿真结果如图2～图5所示。

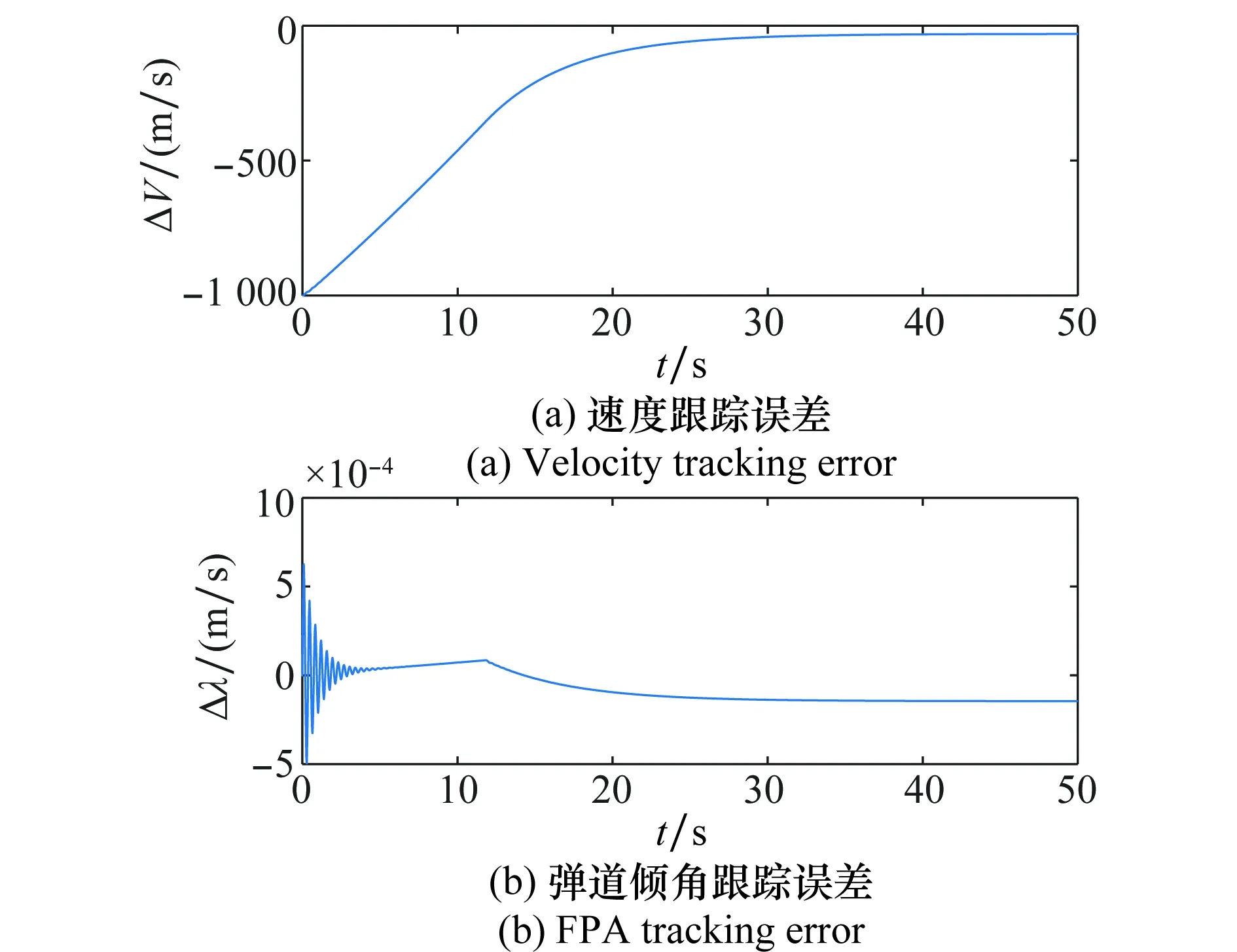
图2 跟踪误差Fig.2 Tracking errors

可以看出,采用文中提出的基于模型正则形式的状态反馈控制时,系统最终弹道倾角的稳态误差远远小于采用传统反步法控制时的稳态弹道倾角误差。

图3 姿态角响应曲线Fig.3 Pitch response curve of attitude angle

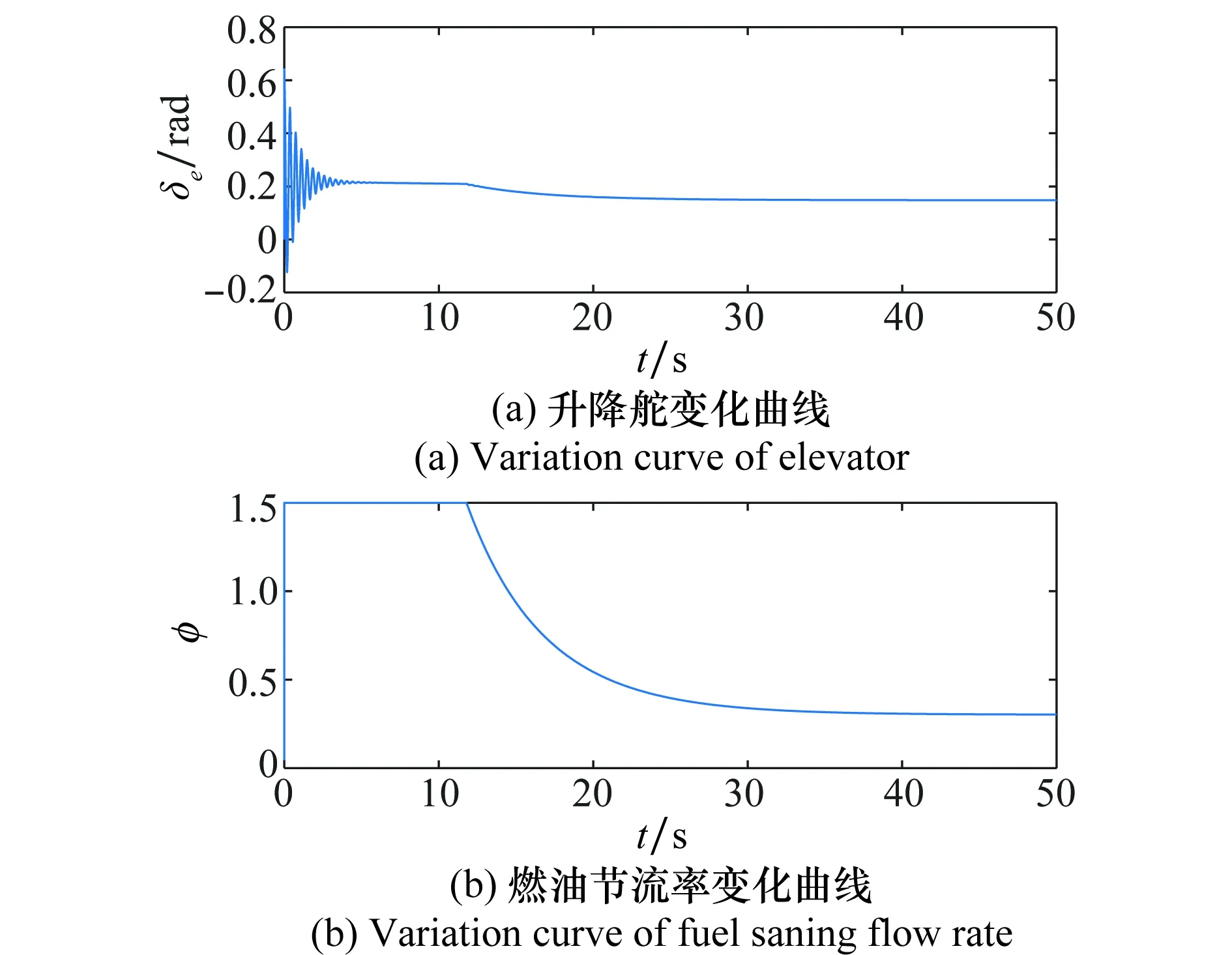
图4 舵偏角和油门变化曲线Fig.4 Variation curve of rudder angle and throttle

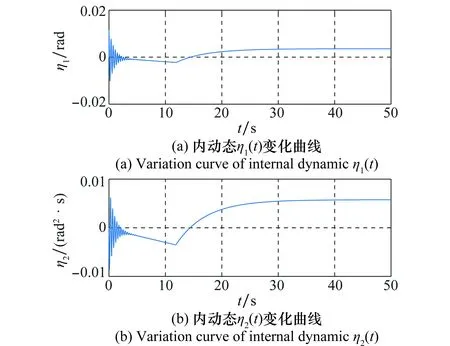
图5 内动态变化曲线Fig.5 Variation curve of internal dynamics

飞行器在25 s左右达到稳定跟踪,跟踪效果良好,误差和收敛速度均在可接受范围内。图3～图5中状态在12 s左右的拐点为燃油节流率由饱和状态转为非饱和状态所致。图3为飞行器俯仰角和攻角的变化曲线,各状态在最初短暂的振荡后趋于平稳,并且整个过程都处在可行约束范围内。图4为舵偏角与燃油节流率的变化曲线,舵偏角最终稳定在0.16 rad左右,由于加速指令在前12 s处于饱和状态,燃油节流率在25 s以后稳定在0.3左右。图5为高度子系统二阶内动态的变化曲线,从图中可以看出,系统的内动态得到了有效的镇定,在25 s左右都收敛到一个稳定值。

仿真结果证明，所设计控制器可以在保证系统外部状态跟踪效果的同时,有效地镇定系统的不稳定内动态,解决了高超声速飞行器高度子系统的非最小相位问题。

需要强调的是,文中所设计控制器重点在于提出一种新方法来解决高超声速飞行器的高度子系统的非最小相位问题,镇定系统的不稳定内动态,暂时并未考虑系统鲁棒性、收敛性能等问题。文中模型正则变换后,只结合简单控制方法来实现系统镇定,后期会在此研究基础上加入非线性干扰观测器,或结合一些鲁棒性强的控制方法来解决系统的鲁棒性问题,所设计控制器会适应更大范围、更强干扰的飞行条件。

5 结 论

针对一类具有非最小相位特性的吸气式高超声速飞行器提出了一个判定非线性系统为非最小相位系统的判据,并针对非最小相位系统的纵向轨迹跟踪控制问题,给出了一种跟踪控制方法,成功地镇定了系统的内动态。

方法的意义在于提出基于模型正则变换后的状态反馈方法来解决高超声速飞行器的高度子系统的非最小相位问题。方法给出了吸气式高超声速飞行器系统非最小相位特性与系统气动参数之间的定量判据;通过转换纵向俯仰通道模型转换为正则形式,实现了内动态的镇定,同时避免反步法的微分爆炸问题,控制器设计过程较为简单。所提出控制方法依赖于精确模型的推导,会产生系统鲁棒性问题。鲁棒控制方法与本文提出方法的结合应用是接下来的研究方向。

参考文献：

[1] 包为民. 航天飞行器控制技术研究现状与发展趋势[J]. 自动化学报, 2013, 39(6): 697-702.

BAO W M. Present situation and development tendency of aerospace control techniques[J].Acta Automatica Sinica,2013,39(6):697-702.

[2] BYRNES C I, ISIDORI A, WILLEMS J C. Passivity, feedback equivalence and the global stabilization of minimum phase nonlinear systems[J].IEEE Trans.on Automatic Control,2002,36(11): 1228-1240.

[3] FIDAN B, KUIPERS M, IOANNOU P A, et al. Longitudinal motion control of air-breathing hypersonic vehicles based on time-varying models[C]∥Proc.of the 14th AIAA/AHI Space Planes and Hypersonic Systems and Technologies Conference, 2006: 8074-8086.

[4] GROVES K P, SIGTHORSSON D O, SERRANI A, et al. Reference command tracking for a linearized model of an air-breathing hypersonic vehicle[C]∥Proc.of the AIAA Guidance, Navigation, and Control Conference and Exhibit, 2005: 6144-6157.

[5] LEVIN J, IOANNOU P, MIRMIRANI M. Adaptive mode suppression scheme for an aeroelastic air-breathing hypersonic cruise vehicle[C]∥Proc.of the AIAA Guidance, Navigation and Control Conference and Exhibit, 2008: 7137-7148.

[6] XU H, MIRMIRANI M D, IOANNOU P A. Adaptive sliding mode control design for a hypersonic flight vehicle[J]. Journal of Guidance Control and Dynamics, 2004, 27(5): 829-838.

[7] XU H, WU L, HU C, et al. Adaptive sliding mode tracking control for a flexible air-breathing hypersonic vehicle[J]. Journal of the Franklin Institute, 2012, 349(2): 559-577.

[8] LEE H, REIMAN S, DILLION C, et al. Robust nonlinear dynamic inversion control for a hypersonic cruise vehicle[C]∥Proc.of the AIAA Guidance, Navigation and Control Conference and Exhibit, 2007: 6685-6693.

[9] PARKER J, SERRANI A, YURKOVICH S, et al. Approximate feedback linearization of an air-breathing hypersonic vehicle[C]∥Proc.of the AIAA Guidance, Navigation, and Control Conference and Exhibit, 2006: 6556-6571.

[10] SIGTHORSSON D O, JANKOVSKY P, SERRANI A, et al. Robust linear output feedback control of an air-breathing hypersonic vehicle[J]. Journal of Guidance Control and Dynamics, 2008, 31(4): 1052-1066.

[11] WALLNER E M, WELL K H. Attitude control of a reentry vehicle with internal dynamics[J]. Journal of Guidance Control and Dynamics, 2003, 26(6):846-854.

[12] 王之, 李惠峰, 包为民. 升力式再入飞行器体襟翼姿态控制方法[J]. 北京航空航天大学学报, 2016, 42(3): 532-541.

WANG Z, LI H F, BAO W M. A body flap attitude control approach of a lifting re-entry vehicle[J]. Journal of Beijing University Aeronautics and Astronautics, 2016, 42(3): 532-541.

[13] WANG Z, BAO W M, LI H F. Second-order dynamic sliding-mode control for non-minimum phase under-actuated hypersonic vehicles[J].IEEE Trans.on Industrial Electronics,2017,64(4): 3105-3112.

[14] FIORENTINI L,SERRANI A,BOLENDER M A,et al.Nonlinear robust adaptive control of flexible air-breathing hypersonic vehicles[J].Journal of Guidance,Control and Dynamics,2009,32(2): 402-417.

[15] SUN H, YANG Z, ZENG J. New tracking-control strategy for air-breathing hypersonic vehicles[J]. Journal of Guidance, Control and Dynamics, 2013, 36(3): 846-859.

[16] 李公军,孟斌.非最小相位高超声速飞行器自适应动态面控制[J].系统科学与数学,2014，34(7):769-779.

LI G J, MENG B. Adaptive dynamic surface control for non-minimum phase hypersonic flight vehicles[J]. Journal of Systems Science and Mathematical Sciences,2014，34(7):769-779.

[17] FIORENTINI L, SERRANI A, BOLENDER M A, et al. Nonlinear control of non-minimum phase hypersonic vehicle models[C]∥Proc.of the American Control Conference, 2009: 3160-3165.

[18] FIORENTINI L, SERRANI A. Adaptive restricted trajectory tracking for a non-minimum phase hypersonic vehicle model[J]. Automatica, 2012, 48(7): 1248-1261.

[19] BOLENDER M A, DOMAN D B. Nonlinear longitudinal dynamical model of an air-breathing hypersonic vehicle[J]. Journal of Spacecraft and Rockets, 2007, 44(2): 374-387.

[20] PARKER J T, SERRANI A, YURKOVICH S, et al. Control-oriented modeling of an air-breathing hypersonic vehicle[J].Journal of Guidance Control & Dynamics,2015,30(3):856-869.