基于PSO的不确定时间序列模体发现算法

王 菊,刘付显,靳春杰

(1. 空军工程大学防空反导学院, 陕西 西安 710051;2. 中国人民解放军93527部队, 河北 张家口 075000)

0 引 言

时间序列是一种按照时间先后顺序排列的记录序列,具有很广泛的应用范围,如医药、生物、计算机、金融等[1-2]。而模体是指时间序列中一些相似度很高的时间序列片段[3]。由于模体中包含被研究时间序列的一些很重要信息[4-5],且模体发现(motif discovery,MD)也是分类[6-7]、聚类[8-9]、异常检测[10-11]和规则发现[12-13]等处理时间序列算法的核心,因此MD对于理解、建模和预测隐藏在时间序列背后的系统具有基础性的作用。

目前针对时间序列MD的算法主要可以分为近似型算法和精确型算法2种。近似型算法的计算复杂度较低,是早些年的研究热点,其核心思想是将时间序列划分为一系列小的时间序列片段,并用符号或实数近似地表示这些时间序列片段,典型的算法主要有矩阵逼近的基元枚举(enumeration of motifs through matrix approximation,EMMA)[14]、主题跟踪算法(motif tracking algorithm,MTA)[15]和节省空间算法(space saving algorithm,SS)[16]等。但是这类算法的缺陷在于需要确定大量的参数,且这些参数通常与被研究的时间序列相关。由于精确型算法的计算量非常大,一直以来被认为是不可实现的,直到文献[17]提出了MK算法。基于他们的工作,一些改进算法被陆续提出,但是这些算法的一个共同缺点是需要指定模体的长度。为解决这个问题,文献[18]提出了可以发现不同长度模体的MOEN算法。但是,该算法仍然存在一些缺点有待改进:①运算时间比较长;②只适用于欧式距离;③只能针对确定的时间序列展开研究。

为此,本文提出了基于粒子群(particle swarm optimization,PSO)的不确定时间序列(uncertain time series, UTS)的MD算法,在传统MD算法的基础上,增加了处理不确定性的功能。该算法设计了基于PSO的UTS MD的研究框架,通过对时间序列片段用该时间序列片段的起始时刻和持续时间进行编码和修正,并利用PSO算法在参数设置少、机理简单、收敛速度快、全局优化能力强等方面的优势,实现了对UTS的MD。实验结果表明,本文所提出的算法不仅可发现不同长度的模体,还可根据实际情况采用多种度量方法,且在精度较高的情况下不会占用较大的内存和运行时间。

1 UTS的预处理

1.1 UTS的表示方法

对于UTS的表示方法,一般可分为2种,即离散型和连续型[19]。其中离散型是指UTS中每个时刻的数据点可能取值由一系列离散的采样点组成,且每个采样点以一定的概率出现或服从某种离散型分布;连续型是指UTS中每个时刻的数据点可看作连续型随机变量,他们服从某种一致的连续型概率分布[20]。在实际应用中,连续型的UTS通过采样常常可以转化为离散型UTS,因此本文的主要研究对象为离散型UTS,文中简称为UTS,其定义如下。

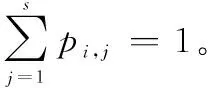
表1 UTS的示例

1.2 UTS的规约

在进行UTS的相似性匹配时,需要把已创建的UTS模型的可能世界都展开成确定的时间序列(certain time series,CTS)。但是由于所得CTS的数量是指数级的,存在组合爆炸的问题,计算量十分巨大。为了解决这个问题,常用的方法是将UTS规约为一条或几条CTS,作为UTS的代表[22]。本文采用以下3种CTS作为对UTS真实值的近似。

定义2(Pmax时间序列)对于长度为n的UTS TSU，其相应的Pmax时间序列是由每个时刻取值概率最大的观察值所构成。例如对于表1中的UTS，Pmax时间序列TSPmax为{0.9,1.3,1.6,1.6}。

定义3(Relative时间序列)对于长度为n的UTS TSU,利用时间序列的连续性,其相应的Relative时间序列是由后一时刻的观察值集合中与前一时刻观察值最接近的观察值所构成,第1个时刻的观察值为该时刻取值概率最大的观察值。例如对于表1中的UTS,Relative时间序列TSRelative为{0.9,0.9,0.8,1.6}。

定义4(Ave时间序列)对于长度为n的UTS TSU,Ave时间序列是由每个时刻观察值集合与其相应概率相乘并求和后的值所构成。例如对于表1中的UTS,Ave时间序列TSAve为{1,1.22,1.3,2.11}。

2 研究框架

基于PSO的UTS MD算法的核心有2个:①如何从UTS中发现更接近实际的模体;②如何将时间序列片段用合适的编码方式表示出来。

基于此,本文通过将UTS同时转化为Pmax时间序列,Relative时间序列和Ave时间序列,并对这3种CTS分别基于PSO进行MD。之后,给定可以容忍的距离比阈值δ,采用投票的方式决定某个时间序列片段是否被输出,并对输出模体中相似度较高的进行合并。其中每个时间序列片段都用该时间序列片段的起始时刻和持续时间表示,并将这两个参数作为粒子编码的对象,其研究框架如图1所示。

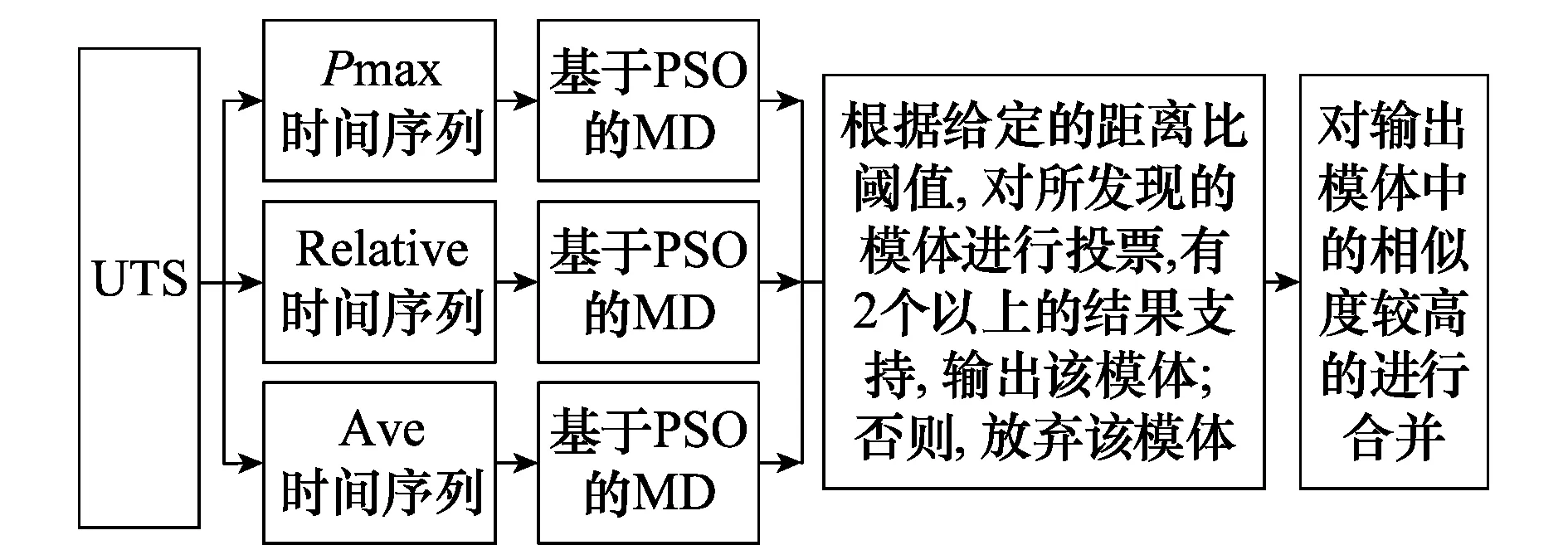
图1 研究框架Fig.1 Research framework

由图1可以看出,基于PSO的UTS MD算法的核心是如何从转化后的CTS中利用PSO算法发现其相应的模体集合,本文将该问题简称为基于PSO的MD,并在下文中关于这个问题展开论述。

3 基于PSO的MD

3.1 粒子编码

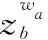
3.2 初始化种群

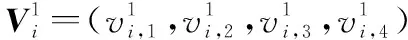
表2 种群的初始化方法

3.3 适应度函数

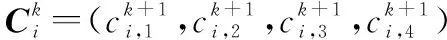
DTW(g,h)=

(1)

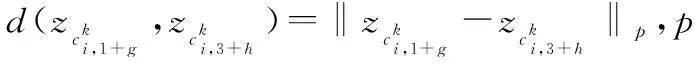
3.4 粒子更新

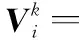
(2)

(3)

式中,ξ是惯性权重;η1和η2是2个学习因子;r1和r2是由(0,1)区间内的均匀随机数组成的4维随机向量;pi=(pi,1,pi,2,pi,3,pi,4)表示第i个粒子在历代中的个体最佳位置;pg=(pg,1,pg,2,pg,3,pg,4)表示在历代种群中所搜索到的最佳位置;·表示点乘,即按照分量逐个做出乘积。

3.5 修正策略

按照第3.4节中的方法对粒子进行更新后,会产生以下3种不具有实际意义的情况:①粒子位置向量中各维的取值不是整数;②粒子位置向量中各维的取值超出了其相应的取值范围;③粒子位置向量中各维的取值不满足相互不重叠的约束条件。为了消除由上述3种情况所产生的无意义的粒子,本文提出了一种修正粒子编码的策略,主要分为以下6个步骤：

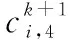
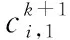
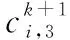
从上述步骤可以看出,所提策略的主要思想是对粒子的合法性进行修正。采用这样的修正策略一方面可以保证种群中的所有粒子都具有实际意义,另一方面可以加快搜索过程,减少运行时间。

3.6 算法流程

上述过程被重复执行,直到满足终止条件,算法流程如图2所示。

图2 基于PSO的MD算法流程Fig.2 Algorithm flow of MD based on PSO

4 实验结果与分析

实验中,采用PSO算法的一般参数设置,即ξ=0.9,η1=η2=2,种群规模popsiza=30,最大迭代次数为1 000。在该参数设置下,首先，用厂轧钢过程中凸度参数的变化情况验证本文所提算法的可行性;其次，文中算法在运行时间、占用内存和收敛性方面与MK[17]和MOEN[18]算法进行了比较,验证了其有效性;由于目前少有关于UTS的MD算法,为验证文中算法的优越性,实验中通过固定文献[23]中算法的窗口,使其退化为基于母题启发多重期望最大化(multiple expectotion-maximization for motif elicitation,MEME)的静态不确定数据MD算法后,在实际数据集和仿真数据集上比较了该算法与文中所提算法在MD准确率上的性能,具体实验数据集和实验结果如下。

本节中所有的算法都用Matlab实现,运行在一台装有64位Windows7操作系统的台式计算机上。该计算机带有2个因特尔酷睿i5-4590处理器和4 GB的RAM。

4.1 实验数据

为验证所提算法的可行性、有效性和优越性,文中实验分别在实际数据集和仿真数据集上进行,他们的构成方法如下。

实际数据集:钢厂轧钢过程中凸度参数的变化情况

在实际钢厂轧钢过程中,将每一卷钢板作为一个周期(约为150个时间点),每一卷的凸度参数变化情况是按时间顺序变化的,具有时间序列的特征。统计100卷的凸度参数变化情况,得到每一时间点的取值是一个可能的集合,将该集合中每个取值所出现的频率视为概率,进而可以得到一个关于凸度参数的UTS。

仿真数据集:带有噪声干扰的UCR时间序列集

UCR是研究CTS的常用数据库,文中主要选取其中的Synthetic Control(60个时间点)、CBF(128个时间点)、OSU Leaf(427个时间点)、Trace(275个时间点)、Wafer(128个时间点)、Beef(470个时间点)、Olive Oil(570个时间点)、Lighting-2(637个时间点)和Adiac(176个时间点)9个数据集为研究对象。为验证所提方法的性能,本文在原始数据的基础上加入了离散均匀分布的噪声进行干扰,将这9个数据集中存储序列变为UTS。

4.2 实例验证

图3是关于凸度参数的UTS。

图3 关于凸度参数的UTSFig.3 UTS on convexity parameters

从图3可以发现,每一个时刻凸度值都对应若干种取值,且每种取值具有不同的概率,因此直接对这样的UTS进行MD时不可能的。根据图1中的研究框架,文中对上述时间序列进行了转化,得到了Pmax时间序列,Relative时间序列和Ave时间序列,如图4所示。

图4 转换后的时间序列Fig.4 Time series after conversion

将wmin和wmax分别设为5和10后,对图4中转换后的3种时间序列分别采用基于PSO的MD算法发现其中的模体,全局最优解所对应的结果如图5所示。

图5 转换后的时间序列及所发现的模体Fig.5 Transformed time series and the found motifs after transform

依次将图5中所示的模体表示为mPmax,mRelative和mAve,为提高所发现模体的精度,他们将进一步通过投票的方式来决定其是否被保留。例如mPmax,投票过程如下:①计算mPmax与Relative时间序列中相应时间片段的DTW距离DTW1及与Ave时间序列中相应时间片段的DTW距离DTW2;②判断|DTW1/DTW2-1|是否大于给定距离比阈值δ=0.1,大于或等于则认为有1个反对者,否则是支持者;③包含自身,当支持者的个数大于2个时,该模体被最终保留,否则被丢弃,因此由于mPmax的支持者为2,其最终被保留。采用同样的方式,可以得到mRelative被丢弃,mAve被保留。进一步地,由于mPmax和mAve所代时间序列片段对的起止时刻基本重合,且该时间段内的凸度值大小基本相同,因此在最终的输出结果中,这2个模体被合并。

4.3 运行时间、占用内存和收敛性分析

为验证所提算法的有效性,针对仿真数据集,本文将不同模体长度下该算法的核心(即基于PSO的MD算法)与Mueen提出的MK和MOEN算法在运行时间、占用内存和收敛性3个方面进行了比较。在比较过程中,文中算法的wmin被设为0,横轴的数值分别对应于文中算法的wmax和MK算法的模体长度。本文对仿真数据集中的确定型时间序列进行了大量实验,发现在不同确定型时间序列下所得的性能结果具有相似性,因此文中仅展示了上述3种算法针对较短时间序列Synthetic Control和较长时间序列OSU Leaf在运行时间、占用内存和收敛性上的结果,分别如图6～图8所示。

由于MOEN算法的一个优势在于可以发现时间序列中任意长度的模体,也就是说发现模体的过程与模体长度无关,因此从图6和图7可以看出,针对不同的确定型时间序列,无论是运行时间还是所占用的内存,随着模体长度的变化都不会发生巨大的变化。

图6 不同模体长度下运行时间的比较Fig.6 Comparison result of runtime under different motif length

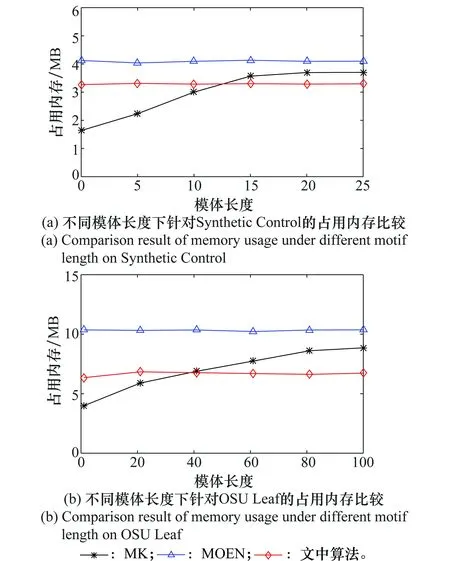
图7 不同模体长度下占用内存的比较Fig.7 Comparison result of memory usage under different motif length

从图6的结果中可以发现MK算法的运行时间随着模体长度的增加一直呈现出上升趋势,文中所提出的算法在一定阶段以后,运行时间随着模体长度的变化趋于不显著。造成这种结果的原因主要有2个:①每当MK算法的模体长度发生变化时,该算法都需要从头开始重新计算,且计算复杂度正比于模体长度;②随着模体长度的增加,本文中所提出的修正策略的作用趋于不显著,整个算法的运行时间趋于稳定。从图7的结果中可以发现本文所提出的算法所占用的内存不随着模体长度的变化而变化,MK算法所占用的内存随着模体长度的增加呈现出增长的趋势,但是不超过MOEN算法所占用的内存。造成这种现象的原因主要有2点:①文中所提算法的内存主要占用于存储种群和最优个体,但是根据文中所采用的编码方式,每个个体只需要用4个参数进行表示,不因模体的长度变化而占用更多的内存;② MK算法所占用的内存主要是用于计算和存储所发现的模体,因此随着模体长度的增加,占用内存呈现上升趋势,但是MK算法只存储了某种特定长度的模体,而MOEN算法需要存储的是符合算法要求的所有长度的模体,因此MK算法所占用的内存要比MOEN算法少。

为了验证所提算法的收敛性,将Synthetic Control和OSU Leaf中模体的长度分别设定为10和50后,对比基于PSO的MD算法和MK算法所发现的模体数量,结果如图8所示。本实验中仅采用MK算法作为对比算法的原因是当模体长度给定时,MOEN算法和MK算法所发现的模体数量是相同的。

图8 收敛性分析Fig.8 Convergence analysis

从图8可以看出,随着迭代次数不断增加,文中所提算法与精确的MK算法所发现的模体数量逐渐趋于相同,表明文中所提算法具有较好的收敛性。说明文中所提算法可以在占用较少的运行时间和内存的情况下快速地收敛于最终的结果,证明了该方法的有效性。

4.4 MD准确率分析

由于目前少有关于UTS的MD算法,为验证文中算法的优越性,实验中首先按照第4.1节的方法,对每一种数据集生成100组UTS,然后固定文献[23]中算法的窗口,使其退化为基于MEME的静态不确定数据MD算法(为便于阐述,下文中简称为MDUS-MEME算法)后,对比了该算法和本文方法所产生的模体集合与上述UTS中实际出现模体的平均重合率,结果如表3所示。

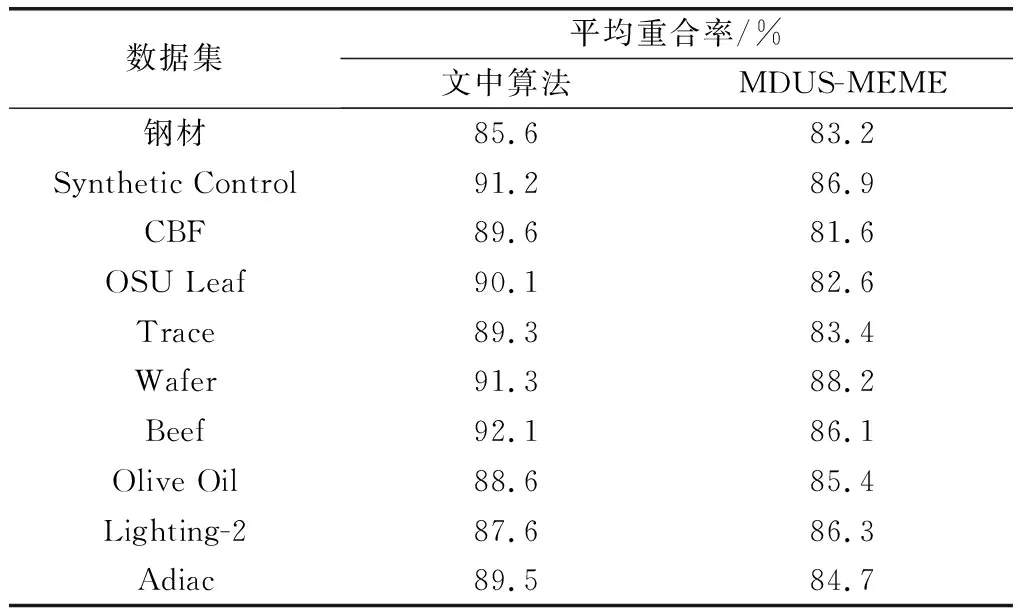
表3 平均重合率比较

从表3可以看出,该算法在这10种数据集上有着较好的平均重合率,表明本文所提算法具有较高的MD准确率,所得模体可以反映出原不确定时间数列的信息。

5 结束语

本文在UTS上提出了基于PSO的MD算法,不仅可以发现不同长度的模体,还可以根据实际情况采用多种度量方法。实验中用实例验证了本文所提算法的可行性,用该算法在运行时间、占用内存、收敛性和MD准确率等方面的性能验证了其有效性和优越性。本文的研究属于探索性研究,不确定性理论、智能搜索算法与MD算法的深入结合将是下一步的研究内容。

参考文献：

[1] 何书元. 应用时间序列分析[M]. 北京: 北京大学出版社, 2004.

HE S Y. Applied time series analysis[M]. Beijing: Peking University press, 2004.

[2] HOPPE C, REINER K. Economic growth and business cycles: a critical comment on detrending time series[J]. Studies in Nonlinear Dynamics and Econometrics, 2017, 5(1): 202-205.

[3] LIN J, KEOGH E, LONARDI S, et al. Finding motifs in time series[C]∥Proc.of the Workshop on Temporal Data Mining, 2002:53-56.

[4] MUEEN A. Time series motif discovery: dimensions and applications[J]. Data Mining and Knowledge Discovery，2014, 4(2): 152-159.

[5] PUNEET A, GAUTAM S, SARMIMALA S, et al. Efficiently discovering frequent motifs in large-scale sensor data[R]. Technical Report, 2015, 1-13.

[6] TORKAMANI S, LOHWEG V. Survey on time series motif discovery[J]. Wiley Interdisciplinary Reviews Data Mining and Knowledge Discovery, 2017, 7(2): 1199.

[7] BUZA K, SCHMIDY-THIEME L. Motif-based classification of time series with Bayesian networks and SVMs[M].Berlin Heidelbeng: Springer, 2009.

[8] CAO D T, ANH D T. A novel clustering-based method for time series discovery under time warping measure[J]. International Journal of Data Science and Analytics, 2017(1): 1-14.

[9] PHU L, ANH D T. Motif-based method for initial the k-means clustering for time series[J]. Journal of Computational and Applied Mathematics, 2012, 236(7): 1733-1742.

[10] TORKAMANI S, DICKS A, LOHWEG V. Anomaly detection and ATMs via time series motif discovery[C]∥Proc.of the IEEE International Conference on Emerging Technologies and Factory Automation, 2016: 6-9.

[11] LIN Y, MCCOOL M D, GHORBANI A A. Time series motif discovery and anomaly detection based on subseries join[J].Laeng International Journal of Computer Science,2010,37(3): 259-271.

[12] MUEEN A. Enumeration of time series motifs of all lengths[C]∥Proc.of the IEEE International Conference on Data Mining, 2013: 547-556.

[13] SCHOKOOHI-YEKTA M, CHEN Y, CAMPANA B, et al. Discovery of meaningful rules in time series[C]∥Proc.of the ACM SIGKKD International Conference on Knowledge Discovery and Data Mining, 2015: 1085-1094.

[14] LIN J, KEOGH E, LONARDI S, et al. Finding motifs in time series[C]∥Proc.of the Workshop on Temporal Data Mining, 2002: 53-56.

[15] LI Y, LIN J. Approximate variable-length time series motif discovery using grammar inference[C]∥Proc.of the International Workshop on Multimedia Data Mining, 2010: 10-15.

[16] CASTRO N, AZEVEDO P. Multi-resolution motif discovery in time series[C]∥Proc.of the SIAM International Conference on Data Mining, 2010: 665-676.

[17] MUEEN A, KEOGH E, ZHU Q, et al. Exact discovery of time series motif[C]∥Proc.of the SIAM International Conference on Data Mining, 2009: 1-12.

[18] ABDULLAH M, NIKAN C. Enumeration of time series motifs of all lengths[J]. Knowledge Information System, 2015, 45: 1050-132.

[19] KRIEGEL H P, KUNATH P, PFEIFLE M, et al. Probabilistic similarity join on uncertain data[C]∥Proc.of the 11th International Conference on Data base Systems for Advanced Applications, 2006: 295-309.

[20] BARBAR D, GAREIA-MOLINA H, PORTER D. The management of probabilistic data[J]. IEEE Trans. Knowledge and Data Engineering, 1992, 4(5): 487-502.

[21] SANNA A, NABAR S, WIDOM J. Representing uncertain data: uniqueness, equivalence, minimization, and approximation[J]. Technical Report, 2005: 1-15.

[22] 宋转,廖小飞,肖瑞. 不确定时间序列的相似性匹配研究[J]. 计算机应用研究, 2014, 34(11): 3349-3352.

SONG Z, LIAO X F, XIAO R. Similarity matching for uncertain time series[J]. Application Research of Computers, 2014, 34(11): 3349-3352.

[23] 王菊,刘付显,靳春杰，等. 一种面向不确定数据流的模体发现算法[J]. 电子科技大学学报,2017,46(1): 81-87.

WANG J, LIU F X, JIN C J, et al. New motif discovery algorithm for uncertain data stream[J]. Journal of University of Electronic Science and Technology of China, 2017, 46(1): 81-87.