基于网络模体特征攻击的网络抗毁性研究

贾承丰，韩 华，完颜娟，吕亚楠

(武汉理工大学理学院，武汉 430070)

0 引言

近年来，有关复杂网络的研究备受各领域研究者的关注。而网络的抗毁性研究一直是研究学者关注的重点。从Barabási[1]研究发现真实网络中具备无标度、小世界等特征开始，人们更加关注对于不同类型网络在面对不同攻击策略时所表现出的抗毁性。Albert和Barabási[2]等人最先研究了针对网络中表现出的不同的拓扑特征，提出了以移除节点为基础的蓄意攻击和随机攻击策略。Holme[3]等人则分别考虑攻击点和攻击边的情况，根据度和介数提出不同的攻击策略。Rinaldi S M等人[4]综合考虑了点和边的相互影响，提出网络中若有某一个节点受到攻击，就会导致一系列的边和点的相继失效，网络间的联系会将故障的影响传播和放大，最终一个很小的故障就有可能对整个系统造成灾难性后果。王仁全[5]提出了以网络的自然连通度为指标，根据不同的局部信息，对点和边进行不同策略的点、边攻击，揭示了不同网络结构与网络抗毁性之间的规律。

然而上述有关网络抗毁性研究的攻击对象都是分别或者综合考虑点和边，但复杂系统中的组成元素不单只有最基本的点和边，模体作为一种网络中反复出现的相互作用的基本模式也吸引了许多研究者对其展开研究。网络模体这一概念最早由R.Moli[6]提出。网络模体是由少量节点按一定拓扑结构形成的网络子图，并且是在真实网络中富集出现的小规模模式。Krumov[7]研究了模体在互联网中优化技术的应用，利用网络的模体特征来优化时序网络的拓扑结构。Squartini和Gah-aschelli[8]以WTO网络为对象，把网络的模体特征作为一种模式识别的手段，揭示了模体对于网络结构的重要性。韩华等人[9]针对网络中存在的模体，提出了模体顶点度与边度的定义，为网络中点和边的重要性提供了基于模体特征的衡量指标。Wen J X等人[10]研究社交网络中的信息传播，揭示了三节点模体对于依赖网络中的传播稳定性有着重要地位。吴翎燕等人[11]从网络的模体结构分析了构建的网络的拓扑结构稳定，并以此对构建股票网络进行推广运用。

随着模体研究在真实网络拓扑结构分析的深入，人们意识到包含大量模体的真实网络的失效方式不能仅仅按照传统的点边失效方式来考虑，所以本文提出了在含有模体的网络中以网络模体作为基元来考虑网络的失效方式，并以代数角度推导模体度的算法，针对模体度设计模体攻击策略，并与传统的攻击手段进行对比，旨在揭示具有模体特征的网络在模体攻击下表现出的抗毁性。

1 模体检验理论

1.1 模体的定义

模体是一种网络子图，是复杂系统中的“小系统”，它的大小介于网络节点和社团之间，是真实网络比随机网络中更频繁出现的小规模模式，属于网络的基本拓扑结构之一。模体在真实网络中出现的频率远远高于在具有相同节点和连线数的随机网络中的出现频率[12]。在大多数的网络中，最为常见的是由3个节点和4个节点构成的模体，示意图如图1、图2所示。

图1 网络三节点模体示例

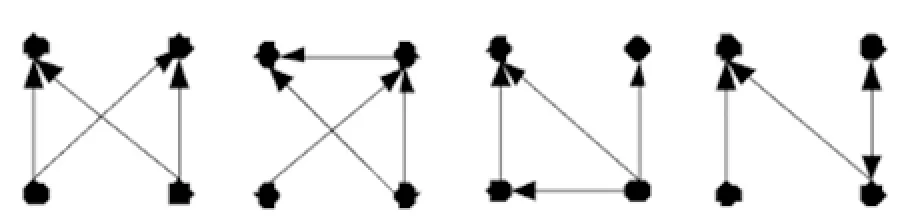
图2 网络四节点模体示例

1.2 模体的统计特征以及存在性检验

1)模体的频率：如果子图M是网络的模体，那么公式(1)称为模体的频率[6]。

(1)

其中，n(M)表示具有n个节点的模体M在实际网络中出现的次数，N表示所有n节点的子图出现的总次数。

2)模体的P值：模体M在具有相同节点的随机网络中出现的次数大于实际网络中出现次数的概率。P值越小，则该网络具有越明显的模体特征[6]。

3)模体的Z得分：对于模体Mi，它在真实网络中出现的次数记为Nreali，它在随机网络中出现的次数记为Nrandi，Nrandi的平均值记为，标准差为σrandi那么模体Mi在该真实网络中的Z得分[6]为

(2)

根据以上的模体的概念和基本统计特征可以检测网络模体的存在性，并以模体为基础分析网络的结构特征。而本文正是基于网络的模体结构特征，提出了针对模体的攻击策略。

2 基于模体的测度量

以文献[3-5]为代表的传统点、边攻击方式中,都直接或者间接地运用节点度作为攻击依据，从而进行随机或者蓄意攻击。然而针对以模体为对象的模体攻击方式，一种新的测度量指标的提出势在必行。

2.1 模体度的提出

度既是网络中重要的概念，也是网络中节点重要性的衡量指标。节点i的度ki定义为该节点的邻边的数目。从网络抗毁性的角度来说，度越大代表该节点越重要，攻击此节点对于网络的破坏性越强。

2.2 三角模体度代数算法

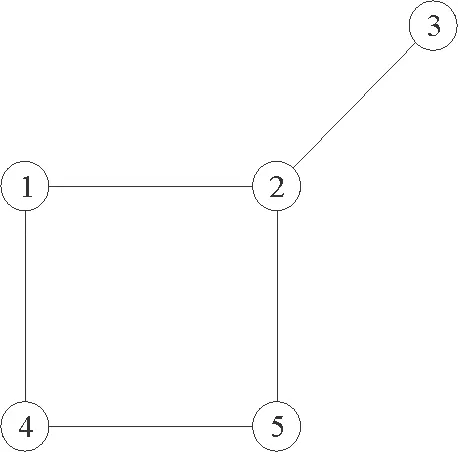
图3 模体代数算法图例

以图3为例，该图是一个无向图，表明它的邻接矩阵是一个对称矩阵。

设aij为矩阵A中的元素，那么aij在图中的含义即是第i个点到第j个点有连边，又因为该图中没有自环和重边，所以邻接矩阵所有元素只可能是0或者1。那aij又可以理解为：由i点到j点走一条边，可以有aij种走法。

通过上述过程就能推广到A2。记B=A2,有bij为B中的元素，它的含义是第i个点出发走两条边到达第j个点有bij种走法。考虑特殊情况——对角线元素bii，表示从i走到某点又回到i的路径条数。很显然这就是i点的度(ki)。

ki=bii

(3)

除了第i行元素相加之和这一求度方法，求邻接矩阵平方的对角线元素又是另一种的求度的方法。

有了上面的过程，记C=A3，C中的每一个元素cij，表示的就是从i点到j点走三条边的路径条数。还是考虑对角线元素cii，也就是从i出发到达i点，走三条边的路径条数。很显然上面的这样的路径就是一个三角模体。由于路径含有有向性，同一个三角模体，路径会以顺时针和逆时针两种方向经过，所以第i个点的三节点模体度(kM3(i))公式有：

kM3(i)=cii/2

(4)

这就把模体度与邻接矩阵联系起来。

2.3 四边模体度代数算法

四节点模体有很多形态，但由Milo[6]研究得知，含有三角形的四节点模体与三节点模体有很大的联系，所以考虑四节点模体时不考虑含有三角形的四点模体，本文以下出现的四点模体全部是四边形模体。

记D=A4，同样，D中的每一个元素dij，表示的就是从i点到j点走四条边的路径条数。为了研究四点模体，来考虑对角线元素dii。也即是从i点出发到i点，走四条边的路径条数。这样就有以下几种情况：

1)路径刚好是一个四边形，也即是四点模体，如路径1→2→5→4→1；

2)路径走了一条边四次，如路径1→2→1→2→1；

3)路径走了两条不同的边两次，如路径1→2→5→2→1。

基于以上3种情况都属于走四条边的路径，但只有情形1)对求出四点模体有意义。排除情况2)3)可以导出第i点的四点模体度(kM4(i))公式有：

(5)

通过上述的模体度算法，就可以对模体节点提供了新的测量度，然后针对模体度这一新的测度，提出不同的针对模体的攻击策略。

3 模体攻击抗毁性研究

3.1 模体攻击策略

不同于传统攻击方式中的点边失效，现实生活中还有很多关于模体的失效机制。如三节点的蛋白酶网络，三节点作为一个整体不仅与外部节点有相互作用，三节点之间也有相互作用的关系，缺失一个节点，就会导致此三节点的相互作用失效，从而蛋白酶分子就失效[13-14]；移动传输BOSS三节点系统，系统元件中三节点之间相互传输信息，若一个节点失效，此传输系统元件失效[15]；mRNA转录遗传密码时，由三个核苷酸编译一个蛋白，在三个核苷酸完整的情况下才能保证完整的编译，若其中一个失效，则该mRNA段失去编译功能[16]。又如电子线路中的四边形模式中，一个电路元件的过压会导致小的电路模式的过压[17]。

基于上述研究和事实的网络失效方式，本文提出了一种针对模体特性的失效方式和攻击策略。模体攻击的失效方式是：攻击一个模体点后，与模体点相连的边失效，并且包含该点的模体也失效。即设网络为G(V,E)，其中V为网络中节点的集合，E为网络中边的集合，设M0为检测到的模体，若节点v0受到攻击，除了与v0相连的e失效，另外还有对于所有的M0⊇v0，其中的e0⊆M0全失效。

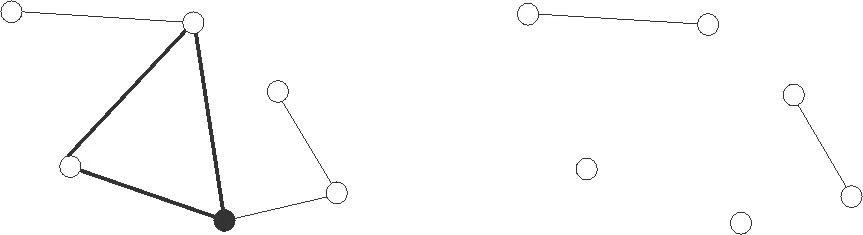
图4 模体攻击示意图

图4中的黑色节点为受到攻击的点，黑色粗边是包含该点的模体，在该点受到攻击后，除了与该点相连的边失效之外，该点所在模体中的边也相应失效。

攻击策略则是根据模体度的大小进行模体蓄意(MIA)和模体随机(MRA)两种不同方式的攻击。模体蓄意攻击是把节点按模体度的大小进行排序，优先攻击模体度大的节点；模体随机攻击则是随机挑选节点进行攻击。将两种模体攻击方式与传统的蓄意攻击(IA)和随机攻击(RA)对比。同样是分为蓄意攻击和随机攻击，传统的点边蓄意攻击策略是依据节点的度，而模体攻击则是模体度。通过网络边连通性指标[18]S(e)得到针对含有模体的网络，模体攻击的效果要优于传统攻击。因为关于模体的网络失效，影响的是点与点之间关系的破裂，也就是说影响的对象是边，所以本文选择的是边连通性，网络连通性指标如下：

S(e)=Ns/Nedge

(6)

其中，Ns为网络攻击后，形成的最大连通子图中所有连边数，Nedge为原始网络中的总边数。

事实上，也可以把两个节点和其连边看成一个两节点的模体，则传统的点边失效方式即是指攻击两点模体中的一个点，与该点相连的模体(也就是与点相连的边)失效，所以传统的点边失效是本文提出的基于模体攻击失效的特殊情况。

3.2 三节点模体攻击实验

1)模体存在性检验

由上述模体攻击的概念可知，只有当网络中显著存在模体时，模体攻击失效才显著区别于传统的点边攻击方式，而且不同的网络具有不同的模体特征，所以在攻击前，首先要检验模体的存在性。本文利用1.2中提出的模体存在性检验手段以及Rand-ESU[19]算法，通过模体发现软件FANMOD，对几种不同规模的虚拟网络(BA网络[1]、ER网络[20])和实证网络(橄榄球网络[21]、人体神经网络[22]、Email网络[23])进行模体存在检验，为接下来的模体攻击奠定基础。只有网络存在模体特征，模体攻击对该网络才有显著的毁坏性。

表1 网络中三角形模体的存在性Tab.1 The existence of triangular motifs in the network

根据表1，Z得分为正数，P值为0，得到以上5种网络都有三角模体特征，可以对其进行模体攻击。

2)模体攻击实验结果

根据模体度的大小，每次攻击一个节点，攻击次数为t，采用蓄意模体攻击(MIA)和随机模体攻击(MRA)以上5种网络，并与传统的蓄意攻击(IA)和随机攻击(RA)作比较。

从图4～图8中，可以得到，从蓄意和随机各角度看，在网络具有模体特征的情况下模体攻击后网络失效速率大于传统的点边攻击；每条曲线与S(e)=0.5的交点代表让网络崩溃的攻击次数的阈值[18]，具体次数由表2体现。可以看出模体攻击次数阈值小于传统的点边攻击次数阈值，说明对于模体攻击，只需要攻击较少的次数就能导致网络的崩溃，网络展现出较差的抗毁性。

而特别的，在ER网络(见图4)和橄榄球网络(见图6)中，模体随机攻击的速率甚至高于传统的点蓄意攻击方式，且崩溃阈值也是模体随机攻击小于点蓄意攻击。导致这一现象的原因可以从表1中分析得出，ER网络和橄榄球网络三角模体的平均模体频率较大，这说明网络中大量存在三角模体，像这样模体特征比较明显的网络，用模体攻击效果会更优。进一步说明，模体特征明显的网络在面对模体攻击的时候，表现出较差的抗毁性，且模体特征越明显，网络的抗毁性越差。

图5 不同策略攻击ER网络效果比较Fig.5 Comparison of different strategies to attack ER networks

图6 不同攻击策略攻BA网络效果比较

图7 不同策略攻击橄榄球网络效果比较Fig.7 Comparison of different strategies to attack football networks

图8 不同策略攻击神经网络网络效果比较

3.3 四节点模体攻击实验

针对四节点模体特征的网络，我们有针对性地研究四边形模体。因为许多四节点模体中已经包含了三节点模体，对于包含三节点模体的四节点模体许多性质与三节点模体相同，因为更高层次上的模体通常由其低层次模体的组合来显现[6]。例如在图2中的四节点模体中，只有最后一个不包含三节点模体，其余的都包含。为了避免重复研究，实验中的四节点模体都是四边形模体。

图9 不同策略攻击电子邮件网络效果比较

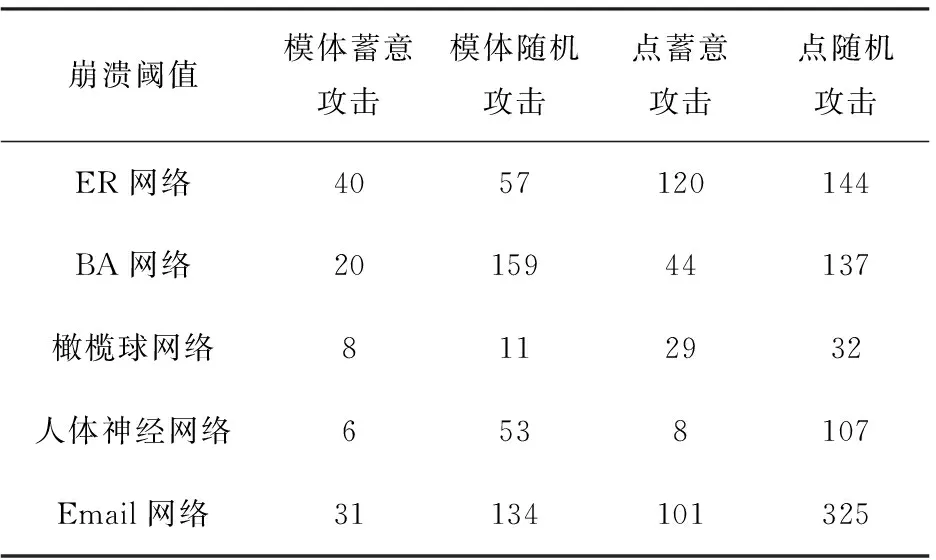
崩溃阈值模体蓄意攻击模体随机攻击点蓄意攻击点随机攻击ER网络4057120144BA网络2015944137橄榄球网络8112932人体神经网络6538107Email网络31134101325

1)模体存在性检验

与三节点模体类似，对一个网络考虑模体攻击，首先要考虑模体在该网络中的存在性，采用虚拟网络和实证网络各两个，接下来利用1.2中提出的模体存在性检验手段以及由Rand-ESU算法，通过模体发现软件FANMOD，对几种网络(BA网络、ER网络、酵母菌网络[24]、美国空军网络[25])进行模体存在检验，为接下来的模体攻击奠定基础。

表3 网络中四边形模体的存在性Tab.3 The existence of quadrilateral motifs in the network

根据表3，由于ER、BA网络的Z得分为负数，P值都为1，可以得到四边形模体不是上述两个网络的模体，或者说这两个网络四边形模体特征并不明显，因为在上述两个虚拟网络中，点与边的联系并不像现实网络中错综复杂，出现四边模体的概率就会很低，所以不考虑用模体攻击的方式。而在酵母菌和美国空军网络中，Z得分为正数，P值为0，可以认为这两种网络具有四边形模体特征，可以对其进行模体攻击。

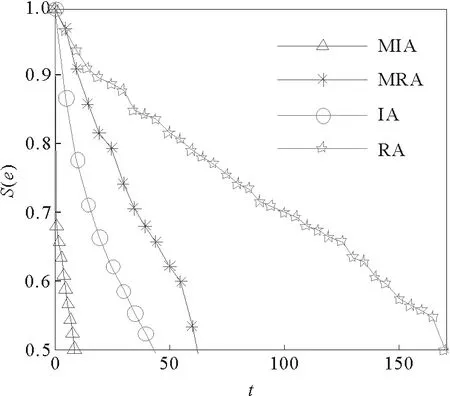
图10 不同策略攻击酵母菌网络效果比较Fig.10 Comparison of different strategies to attack yeast networks

图11 不同策略攻击美国空军网络效果比较Fig.11 Comparison of different strategies to attack USA air networks

2)模体攻击实验结果

与三节点模体攻击类似，根据各模体度的大小，每次攻击一个节点，攻击次数为t作为横坐标，采用蓄意模体攻击(MIA)和随机模体攻击(MRA)以上5种网络，并与传统的蓄意攻击(IA)和随机攻击(RA)手段作比较。

从图9和图10中，可以得到与三节点模体相似的结论，从蓄意和随机各角度看，在网络具有模体特征的情况下模体攻击后网络失效速率快于传统的点攻击；从表4中也可以看出，网络崩溃的阈值是模体攻击小于传统的点攻击，说明对于模体攻击，只需要攻击较少的次数就能导致网络的崩溃，网络展现出较差的抗毁性。

表4 网络崩溃攻击次数阈值Tab.4 Network crash attacks thresholds

4 总结与展望

本文针对有模体特征的网络提出了攻击方式与攻击策略。基于理论和现实中网络的失效方式，发现传统的失效方式并不能与之相适应，因此，在传统攻击失效的基础上，新的模体攻击方式被提出，针对此种攻击方式，又有与传统攻击策略类似的模体攻击策略与之对应。即先根据模体度的大小作为衡量模体节点重要性的一个指标。通过理论推导得到模体度的算法，再根据该指标在有模体特征的网络中进行随机、蓄意攻击，在不同规模、不同类型的网络中发现模体攻击方式优于传统攻击方式。而且网络的模体特征越明显，网络表现出的抗毁性越差。

目前对于含有模体特征的网络抗毁性研究刚刚起步，现有研究了针对模体度对模体节点进行攻击，导致模体特征网络失效。但一方面，衡量模体节点的重要性不仅仅只有模体度，新的衡量指标有待提出。另一方面，模体中还含有关键的边，如果对模体边进行攻击，网络又会呈现出不同的抗毁性，这也是未来亟待解决的研究问题。

[1]Barabasi A L, Albert R. Emergence of scaling in random networks[J]. Science, 1999， 286(5439):509.

[2]Crucitti P, Latora V, Marchiori M, et al. Error and attack tolerance of complex networks[J].Nature, 2004, 340(1-3):388-394.

[3]Holme P,Kim B J,Yoon C N,et al. Attack vulnerability of complex networks.[J]. Physical Review E (Statistical, Nonlinear, and Soft Matter Physics),2002,65(5):056109.

[4]Rinaldi S M, Peerenboom J P, Kelly T K. Identifying, understanding, and analyzing critical infrastructure interdependencies[J]. IEEE Control Systems, 2001, 21(6):11-25.

[5]黄仁全, 李为民, 董雯,等. 不同攻击策略下作战体系网络抗毁性研究[J]. 复杂系统与复杂性科学, 2012, 09(3):62-69.

Huang Renquan, Liweimin, Dong Wen, et al. Research on invulnerability of combat SoS under different attack strategies[J].complex systems and complexity science,2012,09(3):62-69.

[6]Milo R,Shen-Orr S,Itzkovitz S, et al. Alon U. Network motifs: simplebuilding blocks of complex networks[J]. Science,2002,298(5594).

[7]Krumov L. Local Structures Determine Performance Within Complex Network[M]. Darmstadt: Suedwestdeutscher Verlag fuerHochschulschriften,2010.

[8]Squartini T, Garlaschelli D. Triadic motifs and dyadic self-organization in the world trade network[M]// Self-Organizing Systems. Springer Berlin Heidelberg, 2012:24-35.

[9]韩华, 刘婉璐, 吴翎燕. 基于模体的复杂网络测度量研究[J]. 物理学报, 2013， 62(16):168904-168904.

Han Hua, Liu Wanlu, Wu Lingyan. The measurement of complex network base on motif [J].Journal of Physics, 2013, 62(16):168904-168904.

[10] Xie W J, Li M X, Jiang Z Q, et al. Triadic motifs in the dependence networks of virtual societies[J]. Scientific Reports, 2014, 4(14):5244.

[11] 吴翎燕, 韩华, 宋宁宁. 基于相关系数和最佳阈值的股票网络模型构建[J]. 复杂系统与复杂性科学, 2013, 10(4):49-55.

Wu Lingyan, Han Hua, Song Ningning. The construction of stock network model base on correlation coefficient and optimal threshold[J].complex systems and complexity science， 2013, 10(4):49-55.

[12] 张林, 钱冠群, 张莉. 软件系统网络模体及显著性趋势分析[J]. 系统工程理论与实践， 2010, 30(2):361-368.

Zhang Lin, Qian Guanqun, Zhangli. Network motif triad significance profile research on software system[J]. Systems Engineering-theory & Practice, 2010, 30(2):361-368.

[13] 贺勤斌, 刘曾荣. 三节点酶网络相互作用的适应性分析[C]// 全国非线性动力学和运动稳定性学术会议. 2011.

He Qinbin, Liuzengrong, Analyse adaptation of interaction three-node enzyme network[C]// The nonlinear dynamics and motion stability of academic conferences. 2011.

[14] Ma W, Trusina A, El-Samad H, et al. Defining network topologies that can achieve biochemical adaptation[J]. Cell, 2009, 138(4):760-73.

[15] 蒋长彬. 重庆移动BOSS系统三节点高可用性群集的设计与实现[D]. 重庆大学, 2007.

Jiang Changbin. Design and implementation of a three node high availability cluster for chongqing mobile BOSS system[D]. Chongqing University, 2007.

[16] Ross J. mRNA stability in mammalian cells.[J]. Microbiological Reviews, 1995, 59(3):423.

[17] Han J, Yang J, Yang F. Analysis of failure mode on fouble circuit tangent towers in ice disaster area[J]. Building Structure, 2010.

[18] Wang W X, Chen G. Universal robustness characteristic of weighted networks against cascading failure[J]. Physical Review E Statistical Nonlinear & Soft Matter Physics, 2008， 77(2 Pt 2):026101.

[19] Wernicke S, Rasche F. FANMOD: a tool for fast network motif detection[J]. Bioinformatics， 2006, 22(9):1152.

[20] Erdös P, RényiA. On random graphs I[J]. Publicationes Mathematicae, 1959, 6:290-297.

[21] Girvan M， Newman M E J. Community structure in social and biological network. Proc Natl Acad Sci USA.2002: 7821-7826.

[22] White J G, Southgate E, Thompson J N, et al. "The structure of the nervous system of the nematode C. Elegans", Phil. Trans. R. Soc.London 314, 1-340 (1986)

[23] Ebel H, Mielsch L I, Bornholdt S. Scale-free topology of e-mail networks[J]. Phys Rev E Stat Nonlin Soft Matter Phys, 2002, 66(3 Pt 2A):035103.

[24] Bu D, Zhao Y, Cai L, et al. Topological structure analysis of the protein-protein interaction network in budding yeast[J]. Nucleic Acids Research, 2003, 31(9):2443-2450.

[25] Vladimir B, Andrej M. Pajek data [DB/OL].[2017-03-30] http://vlado.fmf.uni-lj.si/pub/networks/data/,2006.