几类传染病模型中基本再生数的计算

崔玉美，陈姗姗，傅新楚

(上海大学数学系，上海 200444)

0 引言

传染病历来是人类健康的大敌，传染病的防治一直是人类社会面临的永恒课题。历史上，如鼠疫、天花、登革热、非典型性肺炎、肺结核、艾滋病等疾病多次肆虐全球，严重威胁着人类的生命安全[1-5]。近年来，诸如梅丽莎、灰鸽子、熊猫烧香、机器狗等计算机病毒的泛滥，因特网、社交网络上各种谣言的传播给人类社会带来了新的威胁和挑战。因此，研究疾病、病毒的传播和扩散机制以及相应的预防措施是当前复杂系统和传染病动力学研究领域的热点问题。早在1760年，D.Bernouli就用数学模型来研究天花的传播。1911年，Ross为研究疟疾传播过程建立的仓室模型为今后传染病动力学的研究奠定了基础。1927年两位数学家Kermack和McKendrick[6]研究黑死病及瘟疫的流行规律，建立了SIR仓室模型，提出预测传染病传播的“阈值定理”，直到今天仍被广泛应用和不断完善。

通过微分方程构建的传染病动力学模型虽然可以刻画许多疾病的动力学行为，然而这种基于均匀混合假设的模型有很大的局限性，它忽略了不同个体传染能力的差异。不论是疾病、计算机病毒或谣言等，他们的传播和扩散必然会受到网络拓扑结构的影响。通过将个体抽象为网络节点，个体间的相互作用关系抽象为节点之间的连边，我们能够更真实地刻画疾病的传播过程。1998年Watts和Strogatz[7]提出小世界网络及1999年Barabasi 和Albert[8]提出无标度网络，自此复杂网络理论获得迅猛发展。众多网络模型的提出和推导为传染病动力学的研究提供了新的方向。其中最经典的有3种：一类是2001年由Pastor-Satorras和Vespignani[9-11]提出的平均场模型；一类是2002年由Newman[12]提出的渗流模型以及相关的分支过程方法和概率生成函数方法；一类是2003年由Wang[13]等人提出的离散概率模型。此外还有对逼近方法[14]、度有效法[15]等等。文献[16]中总结了很多流行病建模的方法，比较全面地分析了这些动力学解析方法的前提假设、具体思路、步骤、及其应用局限。

在传染病动力学模型中，基本再生数R0是十分重要的参量，它表示在无病平衡状态时，引入一个新的染病者，在其平均染病周期内所能感染的人数。R0是决定一种病毒是否流行的标志。基本再生数的计算对疾病的预防和控制、免疫策略等具有指导性的意义。本文主要介绍了传染病模型中基本再生数的导出方法，并且以平均场模型及其相应的衍生模型度相关网络模型、对逼近网络模型、多菌株网络模型、加权网络模型以及时滞微分方程模型传播模型作为实例，计算了其基本再生数。

1 基本再生数的导出方法

我们可以通过以下几种方法导出基本再生数：定义法，根据初始时刻染病者的单调性导出基本再生数，根据正平衡点的存在性导出基本再生数，根据无病平衡点的局部稳定性即通过在无病平衡点处求解再生矩阵或者雅可比矩阵的方法导出基本再生数。

相比较而言，根据定义法导出基本再生数仅适用于比较简单的传染病模型。根据初始时刻染病者的单调性导出基本再生数并不是一个精确地结果，它并不是判断疾病爆发或消亡的充要条件，仅是一个充分条件。根据无病平衡点的局部稳定性，通过计算无病平衡点处的再生矩阵求解基本再生数的方法需要满足一系列的条件[17]，通过计算无病平衡点处的雅克比矩阵求解基本再生数的方法要求所有特征值均具有负实部。所以本文的第二章中以传染病模型中比较典型的几种模型为例子给了出比较精确的导出基本再生数的方法和具体步骤。

1.1 基本再生数的定义及性质

基本再生数R0是刻画传染病发病初期的一个重要参量，它表示在易感者人群中，引入一个染病者，该染病者在其平均染病周期内所能感染的人数的期望。当R0<1时，染病者在其平均染病期内能感染的人数小于1，那么疾病会自行逐渐消亡。当R0>1时，染病者在平均染病期内能传染的人数大于1，则对于SIS类易感者的补充模型，疾病将一直持续形成地方病；而对于SIR模型，患病者数量将出现增长，到达顶峰后再单调减少而最终趋向于零。

随着网络传染病动力学的发展，物理上常用传播阈值λc作为刻画病毒、信息等是否流行的参量，其作用与基本再生数R0是等价的，因为

(1)

当传播率λ<λc即R0<1时，疾病将会消亡；而当传播率λ>λc即R0>1时，疾病将会流行。因此，R0是判断疾病是否流行的重要标准。为控制疾病流行，必须尽量减小R0也就是提高传播阈值λc。

1.2 根据定义导出R0

对于一个常见的总人口恒定的SIR模型：

(2)

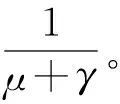
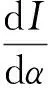
(3)

解上述函数可得I(α)=I(0)e-(μ+γ)α。令ξ表示一个染病者的感染寿命，可以得到概率函数

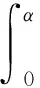
(4)

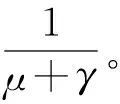
1.3 根据无病平衡点的局部稳定性导出

在本节中仅仅对传统的传染病模型进行一个简单的分析，最常用的方法就是根据无病平衡点的局部稳定性，采用再生矩阵的方法求出基本再生数R0。传统的传染病模型可以看作均匀网络上的传染病模型，则下文中对于网络传染病模型中基本再生数的其他求法当然也适用于传统的传染病模型，在这里就不一一赘述了，在后面会进行详细的介绍。

设有

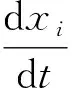
(5)

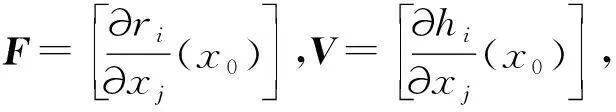
考虑一个一般的SIR模型：

(6)

其中，S，I,R分别为群体中易感者、染病者及恢复(移出)者的个数。这里假定新出生的人口数为A，自然死亡率为d，恢复率为γ，传染率系数为β。很容易求得该模型的无病平衡点为(0,A/d,0)，而且F=βA/d，V=d+γ，则

(7)

上边用再生矩阵方法求解了最简单而且最常见的SIR模型的基本再生数，下面利用同样的方法求解推广的SI模型的基本再生数。

(8)

其中，S,I分别代表群体中易感者、染病者的个数在总人口中所占的比重，显然S+I=1。在该模型中根据不同的感染阶段将I分成m组，易感者被染病者感染进入第1阶段I1，然后I1以一定的感染概率进入第2阶段I2……，一直持续到第m阶段Im，且Im不会再继续传染下去。这里设vi为从i阶段向i+1阶段发展的平均概率，di为染病者在第i阶段的死亡率，b为个体的出生率和易感者的自然死亡率，βk为处于第k阶段的个体的传染率系数。显然，该模型的无病平衡点为(0,…,0,1)，而且可以求得

(9)

(10)

令V-1=(αij)，则

通过计算再生矩阵的谱半径可以求得基本再生数

(11)

1.4 网络传染病模型中由初始时刻染病者单调性导出R0

对于一般的SIR网络传染病动力学模型：

(12)

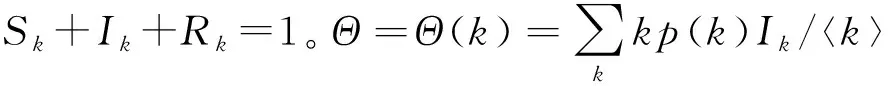
(13)

(14)

1.5 网络传染病模型中由正平衡点的存在性导出R0

对于易感者有补充的模型，当R0>1时，即一个染病者在平均染病期内能传染的人数大于1时，染病者数量逐渐增加，疾病一致持续形成地方病平衡点。则可以根据地方病平衡点的存在性判定疾病是否流行导出基本再生数。这方面工作主要来自文献[18]。对于一般的SIS网络传染病动力学模型：

(15)

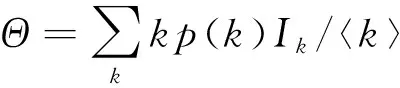
(16)

显然Θ=0始终是该自治方程的一个平凡解。下面导出自治方程(16)存在正解0<Θ<1的条件。

记

(17)

经计算有：

(18)

(19)

则F(Θ)为凹函数，因F(0)=0，且

则F(Θ)=0在(0,1)上有唯一正解的充分必要条件是在Θ=0时有

(20)

从而得到基本再生数：

(21)

当R0>1时，系统(5)存在唯一的正平衡点。

1.6 网络传染病模型中由无病平衡点的稳定性导出R0

根据初始时刻染病者的单调性，或者正平衡点的存在性导出的R0，只是对基本再生数的一种相对粗略的估计。比如根据正平衡点的存在性导出的R0，条件R0>1只能保证方程(15)存在正平衡点，并没有证明该正平衡点的稳定性。也就是说当R0>1时，疾病不一定会持续形成地方病。同理，R0<1只说明方程(15)不存在正平衡点，疾病不一定会逐渐消亡。为导出基本再生数的相对精确的表达式，可以应用微分方程稳定性理论的相关方法[19]。R0作为区分疾病是否流行的参考量，当R0<1时，少量感染者进入系统后疾病会逐渐消亡，即无病平衡点(零解)是局部渐近稳定的。根据系统局部渐近稳定性的条件即可导出R0的表达式。例如对于1.5中的式(15)，

设网络的最大度为n，则该方程在无病平衡点Ik=0处的Jacobian矩阵为

(22)

通过无病平衡点稳定性导出R0是目前最精确的计算传播阈值的方法。但对于相对复杂的微分方程系统，求解无病平衡点处Jacobian矩阵的所有特征值计算量较大，2002年Van den Driessche和Willboordse[17]提出了再生矩阵方法，通过计算再生矩阵的谱半径求得无病平衡点的渐近稳定性，从而导出基本再生数。

对于异质网络模型，记x=(x1,x2,…,xn)t，其中xi>0(i=1,2,…,n)表示每一组个体的数量或者比例。为方便计算将x分成两部分，前m项xi,…,xm表示感染组个体，剩下的xm+1,…,xn为非感染组个体。感染组与非感染组个体的划分应根据流行病学的生物意义，非单纯通过数学方程划分。设有如下微分方程：

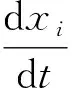
(23)

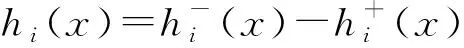
R0=ρ(FV-1)

例如，对于带有出生死亡的异质网络SIR模型：

(24)

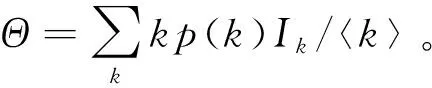
利用再生矩阵的谱半径计算其基本再生数：

胃癌是严重威胁我国居民健康的重大疾病，其发病率居恶性肿瘤第 2 位，死亡率居第 3 位[1]。辨证论治是中医临床诊疗的核心，但目前国内对胃癌的证候尚无统一的认知，也未形成确能提高疗效的共识。因此，基于中医自身的实践性与经验性，在临床中提出新的学术观点并在实践中进行验证，是提高胃癌中医诊治水平的必由之路。海军军医大学（第二军医大学）长征医院中医科作为国家教育部中西医结合临床重点学科，在名老中医魏品康教授带领下，几十年来致力于胃癌的中西医结合防治研究，在实践中提出并构建了较为系统的胃癌痰证理论。

第2步：求方程(24)对应的无病平衡点：

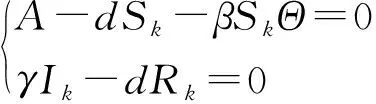
第3步：在无病平衡点E0处求解：

第4步：计算谱半径ρ(FV-1)得，系统(24)的基本再生数为

(25)

1.7 网络传染病模型中由数值估算阈值

对于网络传染病模型的不同理论分析方法，由于分析角度不同，可能会导出不同的基本再生数或者疾病的传播阈值，甚至有些传染病模型不能够通过理论分析求出流行阈值,正确且具体的表达形式。而数值模拟能够更加真实地刻画疾病传播的规律，得到更加真实有效的数据。因此数值模拟是理论分析的一个有效估计和补充，对于求解传染病模型的传播阈值起着非常重要的指导作用。2012年Silvio C. Ferreira等[20]通过对有限网络上SIS模型进行了大量的数值分析，提出可以通过敏感性峰值的方法有效估计传染病的流行阈值，并与异质平均场理论(HMF)、淬火平均场理论(QMF)得到的结果进行了比较分析。2014年Panpan Shu等[21]对其进行了补充说明，针对有限网络上SIR模型提出了估计传染病流行阈值的新方法——变异性峰值方法。2015年Can Liu等[22]将变异性峰值的方法，应用到基于人们行为反应的传染病模型，估计出合理的流行阈值，并且指出了利用平均场方法建模的局限性。本节主要介绍一下参考文献[20],[21]中提出的两种典型的估计传染病流行阈值的方法。

敏感性峰值方法：文献[20]中，将敏感性χ定义为

(26)

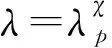
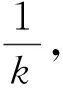
敏感性峰值方法是预测SIS模型流行病阈值的有效方法，但是由于SIR模型中λ>λc时爆发大小的双峰分布导致敏感性峰值方法用于预测SIR模型流行病阈值时，往往高于SIR模型实际的流行病阈值。所以参考文献[21]中提出了预测流行病阈值的新方法——变异性峰值方法。

变异性峰值方法：变异性

(27)

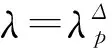
文献[22]通过比较在随机规则网络(RRN)SIS模型、SIR模型中应用变异性峰值方法估计的流行阈值与异质平均场理论(HMF)得到的流行阈值，发现二者是一致的，证明了变异性峰值方法估计SIS模型的流行阈值的准确性。通过研究无标度网络和实际网络Facebook等SIR模型的模拟阈值进一步表明，变异性峰值方法估计流行阈值比敏感性峰值方法准确。

2 几类典型网络传播模型的基本再生数的计算

2.1 度相关网络模型

在研究网络上的动力学行为时，网络的结构对节点的动力学行为具有重要作用。对于现实网络，还有很多情况需要考虑。真实世界网络中节点之间的连接选择并不均等，而是存在明显的偏好。大量实验研究表明[23]，蛋白质交互网络和神经网络等生物网络以及互联网等技术网络是异配的，也就是说网络中度大的节点更倾向于和度小的节点相连。而包括科研人员合作网或者电影演员合作网，微博，Facebook等在内的许多社交网络则多呈现较为明显的同配特性。从社会学与心理学角度分析，精英人士往往更倾向于和不低于自己地位的人交往，从而形成了节点度的正相关性。2002年，Marian Boguna和Romualdo Pastor-Satorras[24]研究了度相关网络动力学模型，并给出了基本再生数的计算方法，本节主要介绍文献[24]，[25]的相关工作。

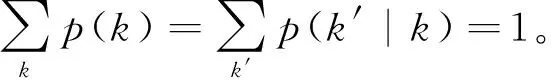
kp(k′|k)p(k)=k′p(k|k′)p(k′)≡〈k〉p(k,k′)

(28)

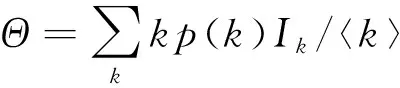
(29)

则Θk表示一条连接度为k的节点的边的另一端指向染病者的概率。由此可以建立度相关异质网络SIS平均场模型：

(30)

其无病平衡点Ik=0，k=1,2,…,n处的Jacobian矩阵L={lkk′}，其中

lkk′=-γδkk′+λkp(k′|k)

(31)

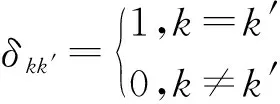
(32)

其中,Λm是网络的连接矩阵C={ckk′}，ckk′=kp(k′|k)的最大特征值。由此可见，度相关网络的基本再生数不仅与网络尺寸有关，还受到网络的相关性的影响，即条件概率p(k′|k)的表达式决定着R0的取值。

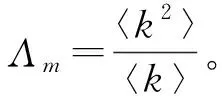
2.2 对逼近网络模型

在考虑传染性疾病在人群中的传播时，疾病的传染只有在染病者(I)和易感者(S)接触(即有边相连)时才可能进行。比如性传播疾病，在忽略同性性行为的假设下，只有异性之间发生性交(即网络中两点相连形成边)时，疾病才有可能传播。基于节点建立的平均场模型不能充分刻画疾病或者信息的传播必须通过网络连边进行这一基本特征。因此科学家建立了以边为研究对象的对逼近(Pair approximation)模型。记[S]、[I]、[SI]分别代表易感者、染病者及二者构成的二元组的数量。如果是完全图，显然有[SI]=[S][I]。但如果不是完全图，则上述微分方程不能封闭，需要给出[SI]随时间变化的动力学方程，这又涉及到[SS]、[II]以及三元组[SSI]等随时间的变化，最终将得到一组无限维的微分方程组。为了对模型进行动力学分析，就需要在误差允许的范围内对方程组进行封闭，这个过程称为“矩封闭”。对逼近是最简单的一种“矩封闭模型”，是关于二元组层面上的封闭，得到的是二元组变化的微分方程组。在矩封闭过程中，必须考虑网络的结构特性。在静态网络中，对于规则网络和节点的度波动不太大的随机网络的研究，已有大量研究成果。

1995年Altmann[26]首次建立了研究性病传播的对关系SIR模型，并利用Markov过程计算疾病传播的基本再生数。随后Keeling和Rand[27]等建立了SEIR对逼近模型来研究麻疹的传播。2001年Filipe[28]提出了正方形逼近方法(SA方法)、对角线逼近方法(DA方法)、混合成对团簇逼近方法(HPA方法)以及Sato团簇逼近方法。2003年Thomson[29]建立了有死亡的SIS网络传染病模型，提出了双边缘的对逼近方法(PEA方法)。2007年，Trapman[30]给出了均匀网络结构下的对封闭模型理论推导，定义了该网络下的有效再生数及其计算方法。下面将结合[30],[31]在均匀网络下建立一般的对逼近模型并求解。

因疾病的传播只有染病者(I)和易感者(S)接触才可能进行，据此可建立总节点数N不变的SIS对逼近传染病模型：

(33)

其中,[S]，[I]，[SI]分别代表易感者，染病者及二者构成二元组的数量。二元组[SI]的存在使方程(33)不能封闭，需要给出[SI]随时间变化的动力学方程。因为节点状态的变化受到与之相连的节点的影响，则根据网络结构可以用三元组来表示二元组[SI]的变化：

(34)

方程右端出现三元组使方程不能封闭，在此做近似截断如下：在均匀网络如ER随机网络中，如果节点的染病者邻居满足多项分布，则三元组[ABC]可由二元组逼近，近似公式为

(35)

其中,n表示网络的最大度。则对(34)中的三元组[SSI]与[ISS]可以近似为

(36)

(37)

将近似等式(36)(38)代入等式(34)封闭方程得到均匀网络下对逼近SIS模型：

(38)

其中,2[SI]+[II]+[SS]=nN,[S]+[I]=N。下面应用再生矩阵谱半径的方法计算R0。

首先求得方程(38)的无病平衡点：

E0=([S]*,[I]*,[SS]*,[SI]*,[II]*)=(N,0,nN,0,0)

(39)

当R0<1时，无病平衡点渐近稳定，疾病趋于消亡；而当R0>1时，平衡点不稳定。

2.3 多菌株网络模型

疾病传播过程中，对于不同的疾病，病菌的传染力和疾病的流行机理不同。传染病往往是多种病原体或多种菌株相互作用的结果。比如引起艾滋病(AIDS)的HIV病毒，有多种互不相同的菌株比如HIV-1，HIV-2等。以下主要根据文献[32]，[33]介绍两种简单的异质网络多菌株传染病模型及其基本再生数的计算。

2.3.1 不同感染力的多菌株SIS模型

在疾病的传播过程中，不同的人群具有相异的感染力。把具有很强传染力的人群称为核心人群。本小节主要介绍S.Nobuaki与A.Kazuyuki在文献[32]中的工作。在易感者与染病者每次接触过程中，易感者Sk一部分以概率1-p转化为具有较弱传染力λ1的一般感染者Uk，其余以概率p转化为具有较强传染力λ2的核感染者Vk。假设网络是度不相关的，在此情形下建立模型：

(40)

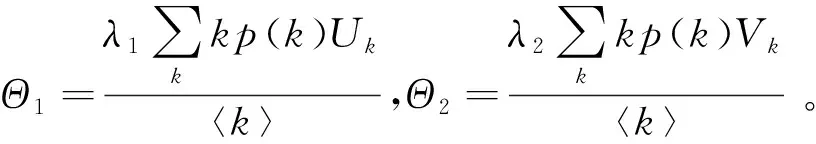
此处用正平衡点存在性导出基本再生数。首先令方程(40)右边等于零，得到模型的正平衡点：

(41)

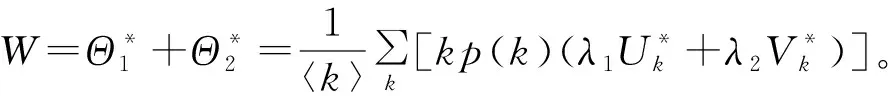
(42)

因为F(0)=0，

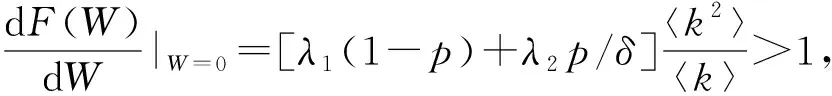
(43)

2.3.2 竞争病毒的SIS模型

在多菌株异质网络传染病模型中，相互作用的两个病毒之间主要存在3种关系：1)Competing pathogens，表示两种病毒相互竞争同一个寄主，不能共存；2)Super-infection，表示在同一个寄主中，一种病毒可以战胜另一种病毒取而代之；3)Co-infection，表示两病毒可以共存于同一个寄主中。以下介绍文献[33]中关于异质网络竞争病毒的SIS模型及其基本再生数的计算。

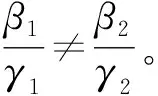
(44)

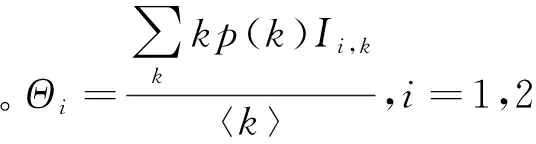
(45)

其中,

(J1)kk′=-γ1δkk′+β1kp(k′)/〈k〉

(46)

(J2)kk′=-γ2δkk′+β2kp(k′)/〈k〉

(47)

(48)

(49)

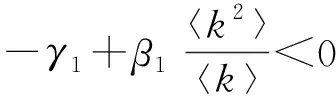
(50)

2.4 带有权重的无标度网络模型

现实世界的真实网络的拓扑结构一般是异质的，大多具有无标度特性，而这种不均匀性不仅表现为连边的数量不同，同时也体现在边上权重的差异。以接触网络为例，接触网络上连边的权重，往往表示连接节点之间的亲密程度或接触时间的长度，从而可以用来衡量疾病传播几率的大小，权重越大，连接的两个节点越亲密，则被感染的概率越大[34-37]。同时，在很多传染病模型中，一定时间内，感染节点能够接触到的邻居数(传染力)为节点度。但实际情况下，感染节点的传染力应该是与节点度有关的函数。文章[38]基于以上两点介绍了无标度网络上带有权重的SIR模型，下面主要介绍该文中对基本再生数的计算。

(51)

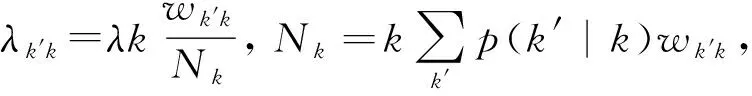
(52)

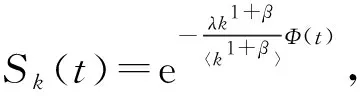
(53)

显然，为了得到基本再生数需要计算出Φ(t)的值。根据(52)及(53)得，

(54)

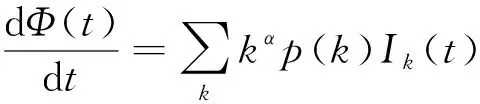
(55)

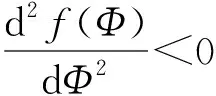
(56)

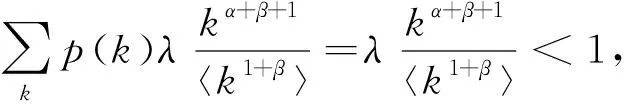
(57)

2.5 时滞微分方程网络模型

常微分方程是研究传染病传播机制和动力学行为的一个重要手段，但这是一种理想化的方法。现实生活中，如流感、SARS病毒、艾滋病、计算机病毒等，虽然一个易感者与一个染病者接触会以一定概率感染疾病，但此时病毒或病菌只是在其体内发展。经过一段时间(即潜伏期)后，才可能具有感染力或表现出症状。另外，染病者患病后也不可能立即恢复成易感者或移除者，这需要一段时间(患病期)的治疗或自我恢复。针对于此，学者们在模型中加入时滞来刻画潜伏期或恢复期对疾病传播的影响。对于经典的传染病模型，这方面的研究成果很多[39]。由于网络模型都是高维微分方程，再将时滞引入模型会使模型变得更加复杂。因此网络中利用时滞模型研究传染病的相关文章很少。文献[40]与文献[41]分别用离散和连续时滞微分方程讨论了异质网络上传染病的动力学行为。这两篇文献所用的求基本再生数的方法相似，我们以文献[40]为例介绍网络时滞微分方程的基本再生数的计算方法。

设网络节点数为保持不变，节点的最大度为。建立带有时滞的SIS微分方程模型，当时有：

(58)

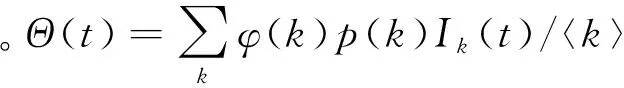
(59)

对等式(59)两边积分可得：

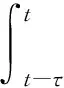
(60)

初始阶段即0≤t≤τ时，系统(59)或(60)服从一般的SI微分方程：

(61)

(62)

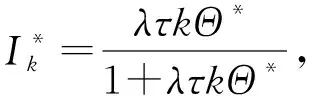
(63)

显然Θ*=0是方程(63)的解，即为该时滞系统的无病平衡点。

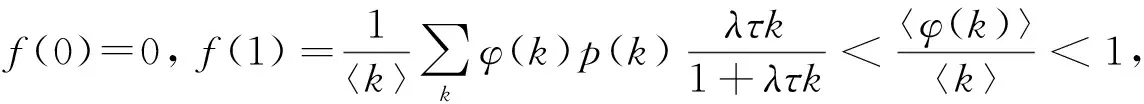
则f(Θ*)是(0,1)上的凸函数，在区间(0,1)上有正解的充要条件是：

由此导出网络上时滞微分方程的基本再生数为

(64)

特别地，考虑年龄结构的网络传播模型和时滞微分方程模型形式是一致的，在导出具有年龄结构的微分方程模型对应的基本再生数时，基本的方法是首先将偏微分方程化成常微分方程，然后通过基本再生数的定义或根据无病平衡点的稳定性来导出年龄结构模型的基本再生数。

2.6 有因病死亡的SIR脉冲预防接种模型

该模型一般根据无病周期解的存在性和局部渐近稳定来求解基本再生数。由于对网络上脉冲接种模型进行分析存在一定的困难,这方面的文献资料还不够完善，所以这里考虑当预防接种在离散的时间点(t=k,k=0,1,2…)以周期为1进行时，可以用以下脉冲系统来修正传统的SIR模型。

(65)

(66)

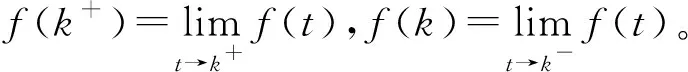
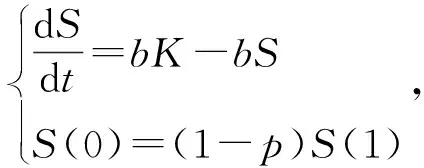
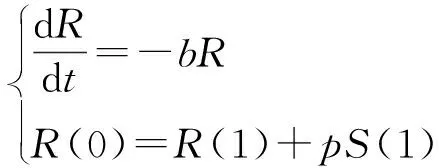
下面讨论无病1周期解的局部渐近稳定性。

引理1[42]设有周期系统

(67)

其中，f∈C[R×Rn,Rn]，φk∈C[Rn,Rn]，f(t+1,y)=f(t,y),∀t∈R；φk+1=φk；且系统(65)关于其周期解y(t)的线性近似系统为

(68)

并设Φ(t)是(68)中方程的一个基解矩阵，即满足

若矩阵M=B1Φ(1)的一切特征根的绝对值均小于1，则系统(68)的零解，也即系统(67)的周期解y(t)局部渐近稳定。

下面做变换x(t)=S(t)-S*(t),y(t)=I(t)-0,z(t)=R(t)-R*(t)，可以得到原系统的关于1周期解(S*(t),0,R*(t))的线性近似系统具有以下形式：

(69)

其基解矩阵为

(70)

其中,

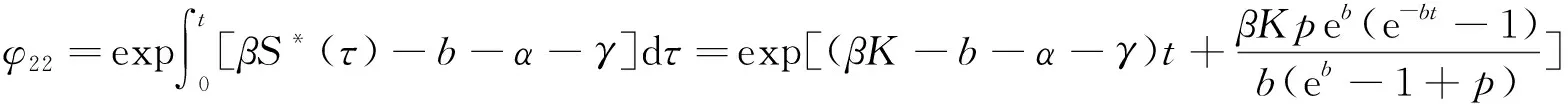
由方程组(66)可得

(71)

应用引理1，

(72)

可以求出M的3个特征根分别为

λ1=(1-p)e-b,λ2=φ22(1),λ2=e-b

由于00,所以0<λ1<1,0<λ3<1,

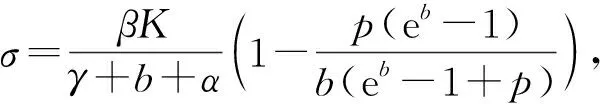
2.7 动态免疫网络模型

在上一节中提到对于网络上的脉冲接种模型的分析是具有一定困难的，目前还没有特别固定的模型和方法供我们使用。在本节中以文献[43]为例，考虑一个动态免疫网络模型的基本再生数的估计方法，利用近似函数根据无病平衡点的稳定性导出基本再生数R0，它为我们估计网络上脉冲接种模型的传播阈值提供了思路。

设网络节点总数为N，而且它可以抽象为一个由点集V和边集E构成的图G=(V,E)。A表示G的邻接矩阵，即当G中节点i和节点j有边相连时，aij=1否则aij=0。

一个节点如果与一个或者多个节点相连时，应该先被免疫。否则，它很有可能被邻居节点所感染，这样的节点称为高危节点。直觉上，我们可以通过控制高危节点来控制疾病的传播。这一模型中主要考虑某一集合Ω中的高危节点，显然⊂Ω⊂V。

文中通过马尔可夫链的方法构建了如下传染病模型:

(73)

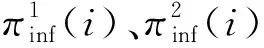
(74)

其中,β为传染率系数，δ为免疫概率，Ν(i)为节点i的邻域，即与节点i有边相连的点的集合。

首先考虑模型的平衡点。由于模型方程的第2个等式和第3个等式都是Ω中节点的方程，所以我们先考虑这两个等式。令这两个等式右端项等于0，且qi,t=qi，pi,t=pi可得pi=0。

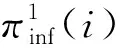
下面我们考虑无病平衡点pi=0，i∈V/Ω的局部稳定性。利用当a<<1，b<<1时(1-a)(1-b)≈1-a-b这一近似，可以把模型简化成以下形式：

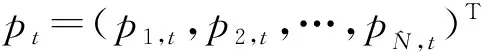
(75)

要使无病平衡点pi=0，i∈V/Ω局部渐进稳定，则

其中ΛmaxA表示矩阵A的最大特征值。该模型的基本再生数

3 时变的基本再生数

以上我们在确定各类参数以后求解的基本再生数都是一个固定的值，而传染病的传播是一个动态的过程，因此基本再生数可能会出现时变的情况。文献[44]表明，不同时期，基本再生数是会发生变化的。这一节我们就根据文献[44]描述的埃博拉病毒的传播特点建立合理的数学模型，通过计算基本再生矩阵的谱半径求出该模型的基本再生数。然后根据该模型中基本再生数的特点，在社区和卫生保健环境中通过调整基本传染率、诊断率和提高感染控制措施，来说明控制干预措施在埃博拉病毒爆发期间的影响。我们将人口分为5类：易感个体(S)、暴露个体(E)、感染个体(I)、住院个体(H)、康复或者死亡后移除个体(R)。具体模型如式(76)。

(76)

其中,N(t)为t时刻的人口总数，β(t)为传染率系数，l(t)量化了与社区中的染病者相比，住院患者的相对传染率。0≤l(t)<1反映了医院隔离措施的有效性，将埃博拉病毒的传播概率降到社区以下。感染个体以依赖于时间的诊断率γa(t)住院或者以概率γI康复而不住院，住院个体概率γR康复。

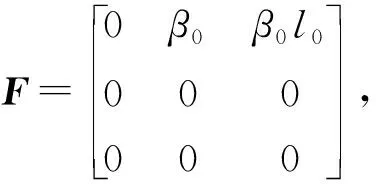
(77)

R0=Rcomm+Rhosp

因为传染率系数β(t)、相对传染率l(t)、诊断率γa(t)均是随时间变化的，所以在埃博拉病毒传播期间，基本再生数也是随时间不断变化的。因此在埃博拉病毒传播期间，埃博拉病毒爆发区域可以通过隔离或者增加防护装备、提高医疗水平等措施，来减少疾病爆发的可能性。这也说明了埃博拉病毒在发达国家不太可能爆发，而在卫生系统极差或者是缺乏的国家比如非洲国家爆发的可能性相对较大。可见当地社会经济和社会文化条件是疾病传播的关键性因素。

4 结论

随着1998年小世界网络及1999年无标度网络在真实系统中的发现和建立，复杂网络上的动力学行为研究是最近科学讨论的一个热点。采用复杂网络理论与流行病学相结合的方法已成为传染病动力学建模的主要趋势。本文总结整理了传染病动力学中基本再生数的几种主要导出方法。即通过基本再生数的定义，初始时刻染病者的单调性，正平衡点的存在性，无病平衡点的稳定性、数值模拟导出基本再生数。作为示例，本文分别介绍了度相关模型，对逼近模型，多菌株模型，加权网络模型和时滞微分方程模型5种网络传播模型，并导出了基本再生数的精确表达式。对于网络传播模型，基本再生数不仅与传染参数(如传染率，恢复率)有关，还与网络拓扑结构有关，而且基本再生数也有能出现时变的情况，因为疾病的爆发过程是一个动态过程，模型参数是随时间在改变的，所以不同时期，基本再生数是会发生变化的。

现有的关于基本再生数的计算方法并不精确，从而使由本文给出的几种方法导出的基本再生数R0不能同时保证当R0<1时疾病消亡，而当R0>1时疾病暴发。这需要进一步分析无病平衡点和正平衡点的全局动力学行为。这将成为今后网络传播动力学研究中的重点和难点。

由于疾病传播方式和网络拓扑结构的多样性，在本文中我们没有办法完全列举出所有传染病模型的基本再生数的导出过程。针对于特殊的传染病模型可能使用几种方法结合考虑才能到较为准确的基本再生数，甚至只能估计出一个基本再生数。但本文所总结的上述方法是主要的，且能够广泛应用于基本再生数的导出，相信这些方法能够给读者提供有益的参考。

感谢课题组的同仁们，特别是孙孟锋的热心帮助和大力支持！

[1]Feng Z L, Jorge X, Velasco-Hernández. Competitive exclusion in a vector-host model for the dengue fever[J]. Journal of Mathematical Biology, 1997, 35: 523-544.

[2]Chan-Yeung M, Xu R H. SARS: epidemiology[J]. Respirology, 2003, 8: 9-14.

[3]Small M, Tse C K, Walker D M. Super-spreaders and the rate of transmission of the SARS virus[J]. Physica D, 2006, 215(2): 146-158.

[4]Castillo-Chavez C, Feng Z L. To treat or not to treat: the case of tuberculosis[J]. Journal of Mathematical Biology, 1997, 35: 629-656.

[5]Castillo-Chavez C, Huang W, Li J. Competitive exclusion in gonorrhea models and other sexually-transmitted diseases[J]. SIAM Journal on Applied Mathematics, 1996, 56: 494-508 .

[6]Kermack W O, Mckendrick A G. Contributions to the mathematical theory of epidemics[J]. Proceedings of the Royal Society A, 1927,115: 700-721.

[7]Watts D J, Strogatz S H. Collective dynamics of small-world networks[J]. Nature, 1998, 393: 440-442.

[8]Barabasi A L, Albert R. Emergence of scaling in random networks[J]. Science, 1999, 286(5439): 509-512.

[9]Pastor-Satorras R, Vespignani A. Epidemic spreading in scale-free networks[J]. Physical Review Letters, 2000, 86: 3200-3203.

[10] Pastor-Satorras R, Vespignani A. Epidemic dynamics in finite size scale-free networks[J]. Physical Review E, 2002, 65(3): 035108.

[11] Pastor-Satorras R, Vespignani A. Epidemic dynamics and endemic states in complex networks[J]. Physical Review E, 2001, 63(6): 066117.

[12] Newman M E J. Spread of epidemic disease on networks[J]. Physical Review E, 2002, 66(1): 016128.

[13] Wang Y, Chakrabarti D, Wang C, et al. Epidemic spreading in real networks: an eigenvalue viewpoint[J]. International Symposium on Reliable Distributed Systems, 2003, 10(13)：25-43.

[14] Eames K T D. Modelling disease spread through random and regular contacts in clustered populations[J]. Theoretical Population Biology, 2008, 73(1): 104-111.

[15] Lindquist J, Ma J, Driessche P V D, et al. Effective degree network disease models[J]. Journal of Mathematical Biology, 2011, 62: 43-164.

[16] 李睿琪, 王伟, 舒盼盼, 等. 复杂网络上流行病传播动力学的爆发阈值解析综述[J]. 复杂系统与复杂性科学, 2016, 13(1):1-39.

Li Ruiqi, Wang Wei, Shu Panpan, et al. Review of threshold theoretical analysis about epidemic spreading dynamics on complex networks[J]. Complex Systems and Complexity Science, 2016, 13(1):1-39.

[17] Van d D P, Watmough J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission[J]. Mathematical Biosciences, 2002, 180(1/2):29-48.

[18] Pastor-Satorras R, Vespignani A. Immunization of complex networks[J]. Physical Review E, 2002, 65(3): 036104.

[19] 马知恩, 周义仓. 常微分方程定性与稳定性方法[M]. 北京: 科学出版社, 2001.

[20] Ferreira S C, Castellano C, Pastor-Satorras R. Epidemic thresholds of the susceptible-infected-susceptible model on networks: a comparison of numerical and theoretical results[J]. Physical Review E, 2012, 86(4): 041125.

[21] Shu P, Wang W, Tang M, et al. Simulated identification of epidemic threshold on finite-size networks[J]. Chaos, 2015, 544(10):167.

[22] Liu C, Xie J R, Chen H S, et al. Interplay between the local information based behavioral responses and the epidemic spreading in complex networks[J]. Chaos, 2015, 25(10): 103111.

[23] Newman M E J. Assortative mixing in networks[J]. Physical Review Letters, 2002, 89(20): 208701.

[24] Boguna M, Pastor-Satorras R. Epidemic spreading in correlated complex networks[J]. Physical Review E, 2002, 66(4): 047104.

[25] Boguna M, Pastor-Satorras R, Vespignani A. Absence of epidemic threshold in scale-free networks with degree correlations[J], Physical Review Letters, 2003, 90(2): 028701.

[26] Altmann M. Susceptible-Infected-Removed epidemic models with dynamic partnerships[J]. Journal of Mathematical Biology, 1995, 33: 661-675.

[27] Keeling M J, Rand D A, Morris A J. Correlation models for childhood epidemics[J]. Proc Biol Sci, 1997, 264(1385): 1149-1156.

[28] Filipe J A N, Gibson G J. Comparing approximations to spatio-temporal models for epidemics with local spread[J]. Bulletin of Mathematical Biology, 2001, 63: 603-624.

[29] Thomson N A, Ellner S P. Pari-edge approximation for heterogeneous lattice population models[J]. Theoretical Population Biology, 2003, 64: 271-280.

[30] Trapman P. Reproduction numbers for epidemics on networks using pair approximation[J]. Mathematical Bioscience, 2007, 210 (2): 464-489.

[31] 靳祯, 孙桂全, 刘茂省. 网络传染病动力学建模分析[M]. 北京: 科学出版社, 2014.

[32] Sugimine N, Aihara K. Stability of an equilibrium state in a multi-infectious type SIS model on a truncated network[J]. Artificial Life Robotics, 2007,11: 157-161.

[33] Wu Q C, Fu X C, Yang M. Epidemic thresholds in a heterogenous population with competing strains[J]. Chinese Physics B, 2011, 20: 046401.

[34] Read J M, Eames K T D, Edmunds W J. Dynamic social networks and the implicatins for the spread of infectious disease[J]. Journal of the Royal Society Interface, 2008, 5(26): 1001-1007.

[35] Barrat A, Barthelemy M, Vespignani A. Weighted evolving networks: coupling topology and weight dynamics[J]. Physical Review Letters, 2004,92(22): 228701-228704.

[36] Boccaletti S, Latorab V, Morenod Y, et al. Complex networks: structure and dynamics[J]. Physics Reports, 2006, 424: 175-308.

[37] Newman M E J. Analysis of weighted networks[J]. Physical Review E, 2004,70(5): 056131

[38] Roshani F, Naimi Y. Effects of degree-biased transmission rate and nonlinear infectivity on rumor spreading in complex social networks[J]. Physical Review E, 2012, 85(3): 036109.

[39] Ma Z E, Li J. Dynamical modeling and analysis of epidemics[J].International Association of Geodesy Symposia, 2009, 106(B11):498.

[40] Xia C Y, Wang Z, Sanz J, et al. Effects of delayed recovery and nonuniform transmission on the spreading of diseases in complex networks[J]. Physica A, 2013, 392: 1577-1585.

[41] Liu Q M, Deng C S, Sun M C. The analysis of an epidemic model with time delay on scale-free networks[J]. Physica A, 2014, 410: 79-87.

[42] Heesterbeek J A P, Roberts M G. Threshold quantities for helminth infections[J]. Journal of Mathematical Biology, 1995, 33(4): 415-434.

[43] Wu Q, Fu X, Jin Z, et al. Influence of dynamic immunization on epidemic spreading in networks[J]. Physica A, 2015, 419:566-574.

[44] Chowell G, Nishiura H. Transmission dynamics and control of Ebola virus disease (EVD): a review[J]. BMC Medicine, 2014, 12(1): 196.