复杂网络中观交通流动态限速控制策略研究
李树彬,傅白白,孙 涛, 党文修, 高 歌
(1.山东警察学院交通管理工程系,济南 250014;2.山东建筑大学a.建筑城规学院,b.交通工程学院,济南 250101;3.山东省公安厅交通管理局,济南 250031)
0 引言
近年来,对复杂性科学的研究已经进入了一个崭新的阶段,渗入到多个学科和领域,成为了系统科学中最前沿、最热点的研究方向,掀起了复杂性科学研究的又一轮热潮。小世界网络和无标度网络是最经典的代表作,于20世纪90年代末发表在著名杂志《Nature》和《Science》上[1-2],并由此引发了一系列的网络结构和动力学相互关系的成果,帮助人们加深了对现实世界的科学认识[3-9]。随着互联网和大数据时代的到来,更是把利用复杂网络研究交通问题引向深入,很多的科学认识指出了现实的交通网络具有小世界特征[10-12]。在这些相关的研究中,基本思路是交通流模型和复杂特性的探讨,尤其是前者自进入新世纪以来,更是蓬勃发展,提出了一系列的新成果[13-23]。有些学者提出了更类似于物理现象的观点[24-29],探讨了交通的动力学特征。之所以选择利用小世界网络研究城市交通问题,是因为城市道路交通网络在一定程度上都具有规则网络上结构的特征,但是随着交通拥堵越来越严重,城市建设速度的加快,越来越多的城市修建了城市快速路、高架快速路以及高架桥等,这就相当于规则网络中引入了长程边,使得城市道路网络具有了一定的小世界特性,因此本文基于小世界网络理论进行可变限速控制策略的研究。
为了更加清晰的认识复杂网络的结构形式,掌握车辆等物质在其上的运动规律,从而为现实的科学服务。需要把研究的重心从交通量的增加驱动网络结构的改变转移到不同的网络结构和控制措施如何影响交通的动力学上来。因此,对于研究城市交通系统的管控措施在不同网络结构上能够产生何种效果以及如何影响交通流的运行都具有十分重要的意义。
虽然在此方面已经有不少的研究成果出现,但是要真正搞清楚交通网络的复杂性机理以及其上的动力学关系,依旧缺乏深层次的理论研究,尤其是对这种传播进行主动控制的技术,较难检索到相关的文献。研究城市交通网络动力学以及拥堵传播的动态趋势是为了制定更好的管控制措施,文献[30]比较系统地分析了不同结构的小世界网络上交通拥堵的传播特性,揭示了网络结构对交通动力学的影响,可以为制定相应的交通管制措施提供理论依据。本文拟在此基础上利用可变限速控制理论与方法探讨不同网络结构上的交通动态情况,以便为交通管理部门提出具有可实际操作性的控制策略。可变限速控制的核心思想就是通过调整限速值对危险交通状态下的驾驶人行为进行主动干预,从而达到改善交通运行状态、降低事故风险、提升行车安全的目的。
近年来,陆续出现了一批主动交通控制系统中有关可变限速控制的研究成果[31-36]。但绝大部分也只是探讨了可变限速控制策略在维护交通安全方面的作用,很少涉及作为主要功能的调流控流的主动交通防御技术。该技术使可变限速不仅可以在交织区、匝道口保障交通安全,更有可能在控制交通系统秩序,确保交通流平稳顺畅运行方面发挥主要作用,从而实现交通管理从被动反应式到主动预防式的转变。本文就是利用复杂网络理论探讨可变限速所能发挥作用的特点,分析城市交通网络上的交通参数的分布状况,以便为交通管理部分制定规划、管控交通秩序提供科学的理论指导,进而合理的制定缓堵和保障交通安全的方案。反之,通过这些研究同样可以提示交通网络的复杂性,发现网络结构的演化机理,为建设基层拓扑提供科技支撑,为交通管理部门提供可靠的决策依据。
1 基于可变限速的中观交通流模型
随着计算机技术的进一步发展,计算机仿真技术已经全面的融入到交通流理论之中,可据此将交通流模型分为两种类型:解析交通流理论和基于仿真的交通流理论。前者具有严密的逻辑推理,可以得到精确的解析结果,如解的存在性、收敛性和唯一性等,便于分析交通流的演化特征。后者对于模型的解析性质没有提出具体的要求,但与实际的道路状况吻合度较高,便于适用到具体的交通实际当中。当然如果将两者进行完美的结合,则是研究交通流理论的最优途径。另一种分类方法则是根据所描述的研究区域范围大小将交通流分为宏观、中观和微观交通流模型,同样的每一种交通流模型都有其优缺点[37-40]。其中,中观交通流模型既具有较高的精度,同时也能够满足计算能力的要求,还具有一定的实时性,因此在近几年的智能交通研究中,引起了越来越多的学者注意。因此本文以中观交通流模型为基础,融合可变限速控制策略来观察复杂网络上的交通动力学特征,以验证网络结构和可变限速控制之间的互动演变关系。
1.1 队列模型
本文采用的队列模型来自文献[30],主要刻画车辆的排队形成与排队的消散过程,记录车辆的位置与时间的对应关系,计算统计车辆的排队延误。同样的,定义c为车道组的输出能力(路段被划分为车道,具有相同性质和作用的几个车道可以定义为一个车道组),交通控制的各种策略以及车队的消散等都可以表现在c的变化上。那么在车队的第i个排队车辆的延误可以表示为
(1)
定义t为小的时间段,那么ct就是该时间段内车道组输出车辆数。如果一个车辆恰好在时刻t这个时间点来到队列末尾,那么它的位置可以表示为:
q(t)=q(0)+l(ct-m)
(2)
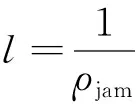
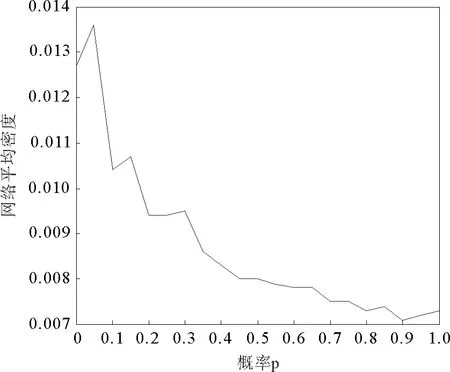
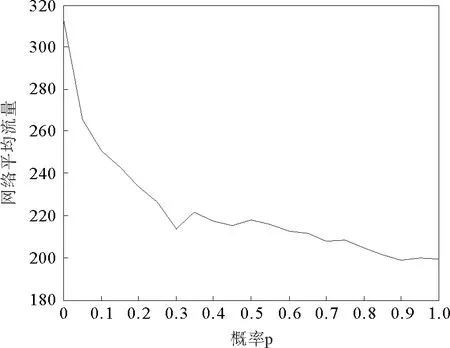
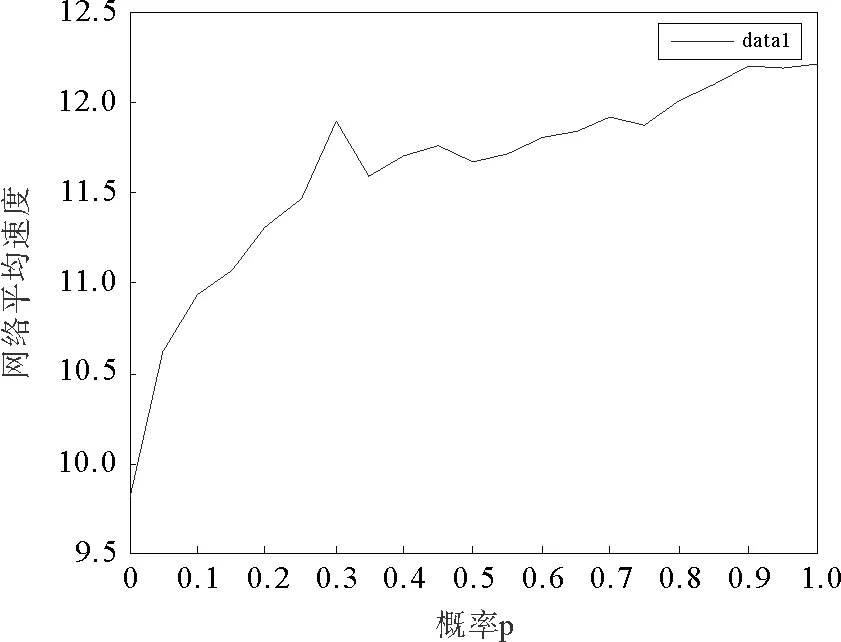
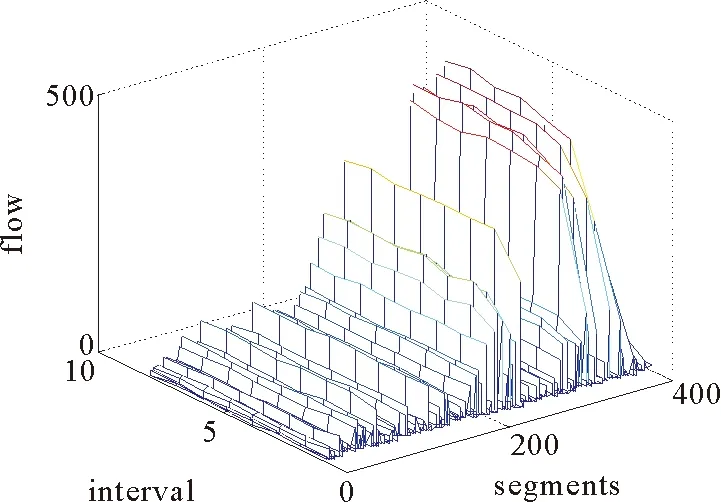
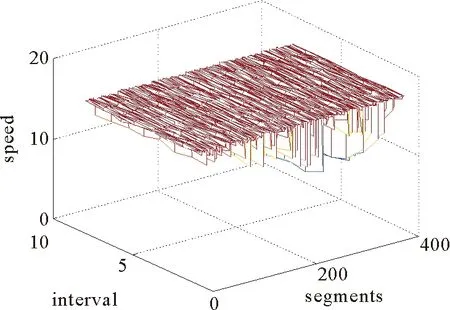
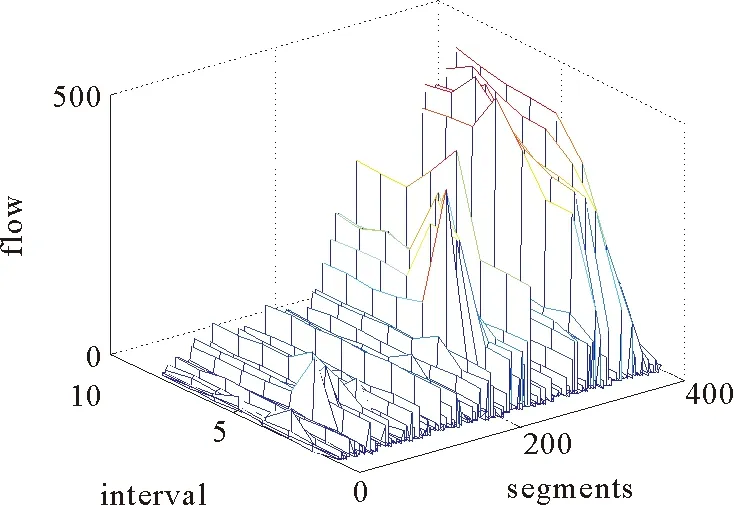
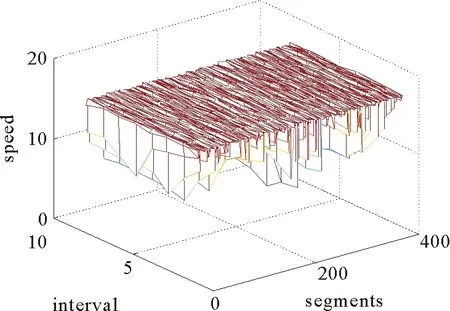
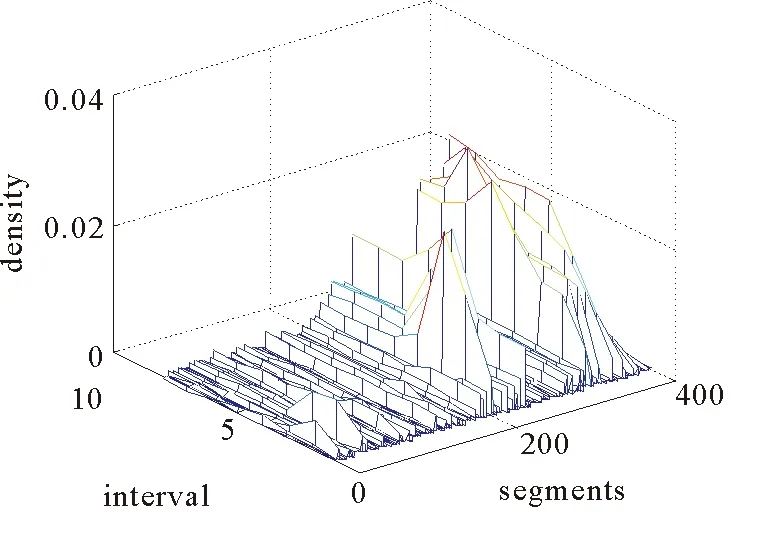
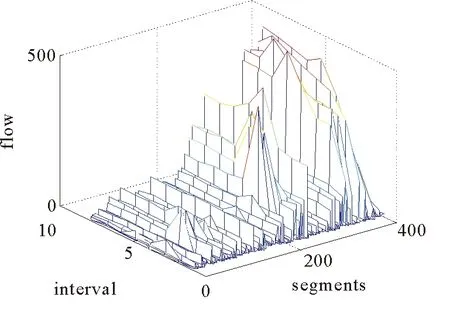
用L表示路段长度,那么模型的约束条件是0 图1 排队模型 大部分交通流模型可以描述spillback现象,如CTM和LTM可以清晰的对其进行展示。本文如图1所示也描述了排队的后溢,当排队超过路段的长队,队列的运动部分变为0,队列开始向上游蔓延。但是这种现象在本文中没有见到,因为本文研究的主要是内容是可变限速对交通流的影响。一旦出现spillback现象,那就说明了车辆出现了排队,车速趋近于0,可变限速没有起到作用。 可变限制速度模型是将可变限速控制的理念引入到原有的速度模型中,使得速度不仅仅符合基本参数的相互关系,更能体现出由于采取控制而使得速度对车辆位置变化的影响。在设计的仿真系统中,通常的交通网络由连接线、节点和交通小区组成。交通小区既是OD点,又是车辆产生或消失的地方;节点为交叉口或者路段的物理性质突变的点;连接线通常是指连接节点的路段,在本文中被划分为具有相同物理性质的节段,节段又可分为车道,在节段的下游处同向同作用的几个车道又被定义为一个车道组,车道组上承载着通行能力的任务。具体是说路段由节段组成,针对每一个节段,这个节段具有相同的物理特性,比如宽度、坡度、车道数等等。在同一个节段上,如果没有出现排队,那么整个节段均按照速度-密度关系模型描述车辆的运动。如果出现排队,那么将该节段分为两个部分,上游为运动单元,即车辆可以运动的部分和排队单位,即下游车辆排队的部分。运动单元内车辆的移动遵从速度-密度模型:为了更接近现实,此时的速度是随着车辆位置的变化而变化的,如图2所示,定义vu为节段上游端点的速度,vd是节段下游端点的速度,Ls是减速区域的长度,跟实际的交通状况密切相关,具体来说,下游如果出现排队,那么上游运动的车辆要想加入排队,那么必然在加入之前有一个减速过程,这个减速区域的长度由车辆的当前速度和和减速度决定,一般情况下设置为固定值Ls,vlim是此时的限速值。 图2 速度变化图 考虑到可变限速的限制,得到位置和速度的下述关系式 (3) 其中 (4) (5) 这里vf是自由流车速;kjam是阻塞密度;k是车流密度;kc是临界密度;α和β是待标定的模型参数,可根据不同的道路和交通实际通过实测获得。 文献[1]中定义了在运动单元中车辆位置和时间的对应关系,在没有排队的情况下,假设t=0时刻,车辆所在的位置是z0,那么在时间t(z)时,车辆的位置在z处,于是符合如下关系: (6) 反之,如果由时间推算,那么在时刻t,车辆的位置为z(t),可以得到如下关系: (7) 这里的λ同样由(4)得到。 当在某个时刻加入可变限速控制时,交通流的运行情况受到了干扰。值得说明的是在减速区内不需要限速,那么限速的强制性也只有从路段的上游节段实施,因此在上游的交通流中,车辆需要按照vu和vlim的较低者行驶,因此得到如下的改进公式: (8) (9) (10) q0,l,c,m的定义同前。 可以看出,在有速度限制的时间内,原有的速-密关系基本图改变了原有的形状,使得交通控制在该时间段内占有主导作用。改进的模型明显更加符合真实的道路状况,同样可以将其推广至其他的控制方式。那么在仿真实验中,采取同样的中观交通流仿真流程[37],区别在于,可以将可变限速值作为初始值作为输入,而对于在线仿真应用的目的下,还可以对这个策略进行在线优化,从而使得最优的交通控制发挥作用,具体的基于可变限速的仿真流程设计如下。 在设计中观交通流仿真流程时,需要注意时间刻度和交通网络大小的划定,如果交通网络过大,可以采用并行计算技术将网络进行切割,从而化大为小以提高精度。同样用T表示仿真时长,Δtupdate为“更新时段长度”,Δtadvance为“进时段长度”前,则存在如下关系: T=kuΔtupdate Δtupdate=kAΔtadvance 其中,kA和ku均为正整数。在Δtupdate时间段内,根据不同节段的物理特性和交通环境状况更新主要参数;在Δtadvance时间段内依据车辆移动模型移动车辆的最新位置,因此设计流程如下: 1)初始化: (1)构建交通网络,定义节点、连接线和节段的物理特性,包括节段的输入输出能力,控制策略等,将对应交通需求车辆加载到正确的位置上,设置时间t=0; (2)按照一定的规则重新定义节点的顺序; (3)设置更新时段的计数器j=0。 2)仿真循环开始: (1)调用更新时段; (2)计数器加1:j=j+ 1; (3)终止性检验:当j=ku时,算法终止。 3)优化技术循环: (1)调用输出信息,包括流量、密度、速度、排队; (2)选取指标,调用优化模型和算法; (3)执行(2),(3)步。 在仿真系统输入中主要包括:网络的具体描述、仿真时长、网络加载时车辆的信息(在网络中的位置、出发地、目的地、当前的路径等)。对于每个更新时段内,需要输入OD流量,即分配矩阵、节段的容量、节段的输入输出能力、如果遇到交通事件,则需要有交通事件的具体描述如严重程度、事发地点和事发事件以及预计消除的时间等。具体流程见图3。路径的产生与存储见文献[37],该算法是一种高效的路径存储结构设计,随时调用最短路径从而达到实时的在线应用的目的。 图3 中观交通仿真流程 将复杂网络的每条连接线分为P若干节段,节段用i表示,将仿真时间K等分,每个时段用k表示显然,p∈P,k∈K。在每个节段上都设置一个监测器,并都包含一个可变限速标志,从而可以获知当前时间的速度密度流量、占有率等信息。第k个时段第p节段的速度、密度、流量分别用vp(k)、ρp(k)、fp(k)来表示,ϑp(k)表示占有率,p减少的方向为行车方向,第p个节段第k个时段的限速值为vlim(p,k),目标函数是研究时段内整个网络的流量最大,那么可变限速优化模型由式(11)确定 (11) vlim(p,k)={20,30,40,50,60,70,80,90} p=1,2,…,P;k=1,2,…K vuplim(p,k)表示根据此时仿真时段的交通状态的最大限速值 ϑp(k)=f(ϑp(k,1),ϑp(k,2),…, (12) vp(k)=f(ρp(k)),p=1,2,…,P;k=1,2,…,K (13) mp表示第p节段包含检测器组数 ρp(k)=f(ϑp(k)),p=1,2,…,P;k=1,2,…,K (14) vlim(p,k)-vlim(p-1,k)≤D(p),p=1,2,…,P;k=1,2,…,K (15) D(p)表示相邻路段的速度差。 因此可变限速值由式(16)确定: vlim(p,k)=min{vuplim(p,k),vlim(p-1,k)+D(p),vp(k)} (16) 该模型的求解可调用Matlab中的牛顿算法。 很多现实的交通网络都呈现出了网络的复杂特征,尤其是对小世界网络的研究引起了一大批学者的兴趣[41-45]。小世界网路的生成算法为: 步骤1初始化,首先构造具有N个节点的最近邻连通环形网络,该初始网络节点都与其左右相邻的个k/2个节点连通(k为偶数)。 步骤2随机重连,以一定的概率p随机重新连接网络中的每条边,并要求不能存在多重边和自连。 本文采用100个节点的网络,由文献[30]的论述可知,选取概率为0,0.5,1为典型的代表网络,分别为规则网络、选择概率为0.5的随机网络,完全随机网络。同样定义V为网路节点的集合(本文中为100个),E代表连接线(边)的集合,G=(V,E)就是网络的拓扑结构,可以描述为一个N×N的关联矩阵{eij},N的大小决定网络的大小,当节点i和j之间有链接关系时eij为1,否则eij为0。3种典型网络图如下图4所示。 图4 3种典型的网络拓扑 由于本文主要探讨可变限速控制策略对交通流的影响,尤其是针对交通安全和交通拥堵的治理,所以本文构建的复杂网络类似城市主干道交通网络,在其主线上实施可变限速的控制。同样将所构建的具有100个节点的网络节点间距定义为500米,单向连接,设置双向两个车道,方阵式排列,根据中观交通流模型的定义要求,将每个节点定义为一个交通小区,为了简便起见将每个单向连接线定义为一个节段,共400个,每个节点均没有设置信号控制。 为了便于研究控制措施对交通演化规律的影响,揭示其内在的本质规律,统一定义交通流模型参数为:拥挤密度0.115 0pcu/m/l,α为1.942 0,β为0.504 0,每个路段的输出输入能力均为0.611v/s。城市快速路设计时速可达到80 km/h,因此可作为最高时速。仿真总时间为3个小时,每15 min一个时段,共12个。交通需求缺少真实的数据,但不影响对本文研究重点的影响,假设OD需求设置即可,经仿真测试,需求为1时网络畅通,个别路段速度偏低,随着需求的逐步增加网络开始变得越来越拥挤。需求设置为3时,网络几乎全线拥堵,因此也不宜实施限速控制,当需求设置为2时,少部分路段拥堵,大部分路段畅通,但平均速度偏低,也不太适宜应用可变限速控制,因此可选取网络较为畅通时的需求1为仿真的基础数据。 在不同的时间段内,部分路段上的可变限速控制策略取不同的值,通过在线优化可得到最优限速值。一般情况下,在拥堵路段拥堵方向的上游速度较快的路段上设置可变信息版用以显示限速值,通常所取限速值比当时的平均路段车流速度低10、20或30等整数速度值,从而简化了优化值取值域使问题相对容易求解。文中拥堵常发路段多数位于介数较大的边上,因此将可变信息版设置在于介数较大的边相连接的上下游路段上,从而控制本路段的车流速度,当出现严重拥堵时将可变信息版设置在次上游的路段上,并依此递增信息板数目。信息板越多控制的范围就越大,信息板位于路段的中心位置。 通过仿真研究,概率p的选取与网络平均速度、密度、流量的关系得到如下关系图5~图7,因此关于可变限速控制的时效性,同样可以选取概率为0、0.5、1的网络作为典型的研究对象。下面具体分析3种网络中在没有可变限速控制和实施可变限速控制时,复杂交通网络的交通流动力特性和传播规律。 图5 网络平均密度与p关系图 图6 网络平均流量与p关系图 图7 需求1时网络平均速度与p关系图 首先从宏观层面考虑整体网络在总仿真时段内的总密度、总流量和总速度和的变化情况,在没有任何控制措施的情况下可以得到:总的旅行时间为3 032.1h,总的出行距离为122 533.7 km,总流量为68 299辆,总延误为989.9 h,最大节点延误是226.4 h;总的平均速度40.4 km/h,网络总密度2.126 6,平均流量是21.519 7。在连接线较长的路段上设置16块可变信息版用以实施可变限速控制,为了测试有效性。因为在无控制状态下,总的平均速度是40.4 km/h,在本次试验中将从7:30分开始,限制速度为30 km/h,那么可以得到如下信息:总的旅行时间为3 386.8 h,总的出行距离为121 821.8 km,总流量为67 811辆,总延误为1 356.4 h,最大节点延误是227.4 h;总的平均速度36 km/h,网络总密度2.281 1,平均流量是21.393 4。 从以上结果可以看出,可变限速控制对交通流的分布和动态特征有较大的影响,由于速度限制的存在必然导致平均速度的降低,总体密度的增加,车辆行驶的总里程数也有所下降,但是可以看到最大节点延误并没有大幅增加。根据相关研究车辆平均速度的降低有利于保障交通安全、减少交通事故的发生。 其次考虑每个仿真时段内每个路段的平均密度、平均流量和平均速度的变化情况,如图8~图13所示。 从图8~图13可以看到密度的分布得到了部分均衡,在同一需求水平下,密度的均衡分布说明网络运行情况较好。在有可变限速控制的路段,流量有了大幅度的降低,但对其他路段影响不大,这说明其他路段并没有因为可变限速而变得拥挤,但同时部分路段得到了安全保证。在有可变信息版的路段,车辆速度均在限制速度之下,这也是实施可变限速的目的之一,即调整交通流。因此可以根据不同的目的采取不同的可变限速控制策略。下面给出可变限速控制优化后的平均速度、平均密度和平均流量的分布情况,如图14~图16。 可以看出,优化后的网络密度得到了均衡,虽然速度略有下降,但流量和延误都变化不大,这说明优化方法既保障了交通安全,又没有造成较大的交通延误,甚至平滑了部分路段,使整体网络交通状况更加畅通。 最后分析在同一优化状态下3种网络结构上的交通动力学特征,从宏观分析来看,p取0.5时,整个仿真时间段内,网络加载的最大车辆数是2 369,整个网络处于畅通状态,用绿色代表路段畅通,红色代表路段拥堵,黄色代表路段拥挤,那么各条路段占网络百分比如图17。对于完全随机网络,加载的最大车辆数是7 269,总的旅行时间为13 152.9 h,总的出行距离为497 218.4 km,总流量为426 219辆,总延误为4 865.9 h,最大节点延误是563.2 h;总的平均速度37.8 km/h。路段状况百分比如图18。同样分析规则网络,仿真时间段内加载的最大车辆数是18 692,总的旅行时间为22 671.6 h,总的出行距离为599 296.3 km,总流量为280 424辆,总延误为13 016.7 h,最大节点延误是410.5 h;总的平均速度25.6 km/h。路段状况百分比如图19。 图8 p=0.5时无控制状态下的节段时段密度情况Fig.8 p=0.5,uncontrolled density of the segments 图9 p=0.5无控制状态下的节段时段流量情况 图10 p=0.5时无控制状态下的节段时速度情况Fig.10 p=0.5,uncontrolled speed of the segments 图11 p=0.5控制状态下的节段时段密度情况 图12 p=0.5时控制状态下的节段时流量情况Fig.12 p=0.5, controlled flow of the segments 图13 p=0.5控制状态下的节段时段速度情况 图14 p=0.5时优化控制状态下的节段时密度情况Fig.14 p=0.5,optimal controlled density of the segments 图15 p=0.5优化控制状态下的节段时段流量情况Fig.15 p=0.5,optimal controlled flow of the segments 图16 p=0.5时优化控制状态下的节段时速度情况Fig.16 p= 0.5, optimal controlled speed of the segments 图17 p=0.5时的网络拥堵状态百分比 图18 p=0时的网络拥堵状态百分比Fig.18 p=0, the percentage of network congestion 图19 p=1时的网络拥堵状态百分比 可以看出在同一需求下,同样面积的网络,同样的节点数,同样在带有可变限速优化的状态下,完全随机网络、规则网络和不同概率的网络交通状况具有巨大的差别。所以不同的网络结构下,应采取不同的控制措施,根据不同的需要对城市交通进行不同的规划,从上述网络状况来看,p=0.5时的网络是最畅通的,因此就城市网络结构来看,格子网络加环线的规划是最好的网络形式。完全随机网络的布局较为复杂,连接线较多,致使复杂网络形式多元化,导致了更加复杂的交通动态,而规则网络由于具有一定顺序性,在最短路选择上车辆具有统一性,因而最为拥堵。 通过观察60个时空图,并且比对相关的数据,可以发现可变限速措施对交通流密度、流量、速度的影响显著,其分布形式在网络中也各具不同的特征,就网络整体而言介数较大的边上密度最大,最容易发生交通拥堵,密度最大的介数边都位于交通需求OD对间的最短路径上。如果介数边上发生交通拥堵,将会引发一系列的连锁反应,对整个交通网络性能影响巨大,因此有必要在介数边以及与介数边相连接的路段上实行可变限速控制措施,即在交叉口上游利用可变限速控制创造自由流区域,使得这个自由流区域的通行能力略小于进口道的通行能力,或者限制车速延缓车辆进入介数边从而减轻交通拥堵堵程度。这就相当于在城市快速路出口上游实施可变限速控制,延缓与地面衔接后出口处的交通压力。 正如前文所述,之所以选择小世界网络作为研究对象,是因为小世界网络的结构复杂性。通过虚构的网络对现实的交通网络进行模拟,改变了部分交通问题的不可实验性。因此这种尝试对交通管理工作具有积极的推动作用,也是智能交通发展的方向之一,同时本文提出的方法还可以用来研究城市交通网络的承载能力。 本文通过引入可变限速控制策略改进了中观交通流仿真模型,并利用复杂网络理论探讨了交通流在不同网络结构上的演变演化规律,提出了可变限速控制的优化模型。挑选了小世界网络中不同重连概率的三种网络进行测试,发现了不同网络拓扑结构上的交通拥堵传播规律,进而可以分析复杂网络上的交通动力学和交通控制策略的相互影响。仿真结果可以看出,可变限速控制策略对保障交通安全以及缓解局部交通拥堵有一定的积极作用,复杂网络介数较大的边上极易发生交通拥堵,在其连接的边上实施可变限速控制策略是有效缓解交通压力的方法之一,同时可以看出,不同拓扑结构网络上的交通流特性具有显著的差异性。本文的研究同样是理想的网络结构,也未获得真实的交通需求,没有考虑其他的交通控制形式,尤其是信号控制和可变限速的结合,这也是需要进一步研究的方向。 [1]Watts D J, Strogatz S H. Collective dynamics of ‘small-world’ networks [J]. Nature, 1998, 393(6684): 440-442. [2]Barabási A L, Albert R. Emergence of scaling in random networks [J]. Science, 1999, 286(5439): 509-512. [3]Cui D, Gao Z Y, Zhao X M. Cascades with coupled map lattices in preferential attachment community networks [J]. Chinese Physics B, 2008, 17(5): 1703-1708. [4]Zhang Z, Fu Z Q, Yan G. Synchronization speed of identical oscillators on community networks [J]. Chinese Physics B, 2009, 18(6): 2209-2212. [5]Cui D, Gao Z Y, Zheng J F. Properties of asymmetrically evolved community networks [J]. Chinese Physics B, 2009, 18(2): 516-521. [6]杜海峰,李树茁, Marcus W F, 等. 小世界网络与无标度网络的社区结构研究 [J]. 物理学报, 2007, 56(12): 6887-6892. Du Haifeng, Li Shuzhuo, Marcus W F,et al. Community structure in small-world and scale-free networks [J]. Acta Physica Sinica, 2007, 56(12): 6887-6892. [7]李季,汪秉宏,蒋品群, 等. 节点数加速增长的复杂网络生长模型 [J]. 物理学报, 2006, 55(8): 4051-4057. Li J, Wang Binghong, Jiang Pinqun,et al. Growing complex network model with acceleratingly increasing number of nodes [J]. Acta Physica Sinica, 2006, 55(8): 4051-4057. [8]赵明,汪秉宏,蒋品群, 等. 复杂网络上动力系统同步的研究进展 [J]. 物理学进展, 2005, 25(3): 273-295. Zhao Ming, Wang Binghong,Jiang Pinqun,et al. Recent advancement in research of synchronization of dynamical systems on complex networks [J]. Progress in physics, 2005, 25(3): 273-295. [9]罗群,吴薇,李丽香, 等. 节点含时滞的不确定复杂网络的自适应同步研究 [J]. 物理学报, 2008, 57(3): 1529-1534. Luo Qun,Wu Wei,Li Lixiang,et al. Adaptive synchronization research on the uncertain complex networks with time-delay [J]. Acta Physica Sinica, 2008, 57(3): 1529-1534. [10] Wu J J, Gao Z Y, Sun H J. Simulation of traffic congestion with SIR model [J]. Modern Physics Letters B, 2004, 18(30): 1537-1542. [11] Wu J J, Gao Z Y, Sun H J. Complexity and efficiency of Beijing transit network [J]. International Journal of Modern Physics B, 2006, 20: 2129. [12] Wu J J, Gao Z Y, Sun H J. Cascade and breakdown in scale-free net-works with community structure [J]. Physical Review E, 2006, 74(6): 066111. [13] Gupta A K, Sharma S. Nonlinear analysis of traffic jams in an anisotropic continuum model [J]. Chinese Physics B, 2010, 19(11): 110503. [14] Gupta A K, Sharma S. Analysis of the wave properties of a new two-lane continuum model with the coupling effect [J]. Chinese Physics B, 2012, 21(1): 015201. [15] Peng G H, Cai X H, Cao B F, et al. A new lattice model of traffic flow with the consideration of the traffic interruption probability [J]. Physica A, 2012, 391(3): 656. [16] 曾友志,张宁,刘利娟. 考虑司机扰动风险偏好异质的跟驰模型 [J]. 物理学报, 2014, 63(6): 378-384. Zeng Youzhi, Zhang Ning, Liu Lijuan. A new car-following model considering drivers’ heterogeneity of the disturbance risk appetite [J]. Acta Physica Sinica, 2014, 63(6): 378-384. [17] 敬明,邓卫,王昊, 等. 基于跟车行为的双车道交通流元胞自动机模型 [J], 物理学报, 2012, 61(24): 323-331. Jing Ming,Deng Wei, Wang Hao,et al. Two-Lane cellular automaton traffic model based on car following behavior [J]. Acta Physica Sinica, 2012, 61(24): 323-331. [18] Lakouari N, Bentaleb K, Ez-Zahraouy H, et al. Correlation velocities in heterogeneous bidirectional cellular automata traffic flow [J]. Physica A:Statistical Mechanics and its Applications, 2015, 439: 132-141. [19] Yang D, Qiu X P, Yu D,et al. A celluar automata model for car-truck heterogeneous traffic flow considering the car-trunk following combination effect [J]. Physica A: Statistical Mechanics and Its Applications, 2015, 424: 62-72. [20] 华雪东,王炜,王昊. 考虑驾驶心理的城市双车道交通流元胞自动机模型 [J]. 物理学报, 2011, 60(8): 084501-084508. Hua Xuedong, Wang Wei, Wang Hao. A two-lane cellular automaton traffic flow model with the influence of driving psychology [J]. Acta Physica Sinica, 2011, 60(8): 084501-084508. [21] 汪秉宏,文旭,许伯铭. 复杂网络 [M]. 上海: 上海科技教育出版社, 2006: 247-261. Wang Binghong H, Wang Wenxu, Xu Boming. Complex Neworks [M]. Shanghai: Shanghai Scientific and Technological Education Press, 2006: 247-261. [22] 华雪东,王炜,王昊. 考虑自适应巡航车辆影响的上匝道系统混合交通流模型 [J]. 物理学报, 2016, 65(8): 084503. Hua Xuedong, Wang Wei, Wang Hao. A hybrid traffic flow model with considering the influence of adaptive cruise control vehicles and on-ramps [J]. Acta Physica Sinica, 2016, 65(8): 084503. [23] 华雪东,王炜,王昊. 考虑车与车互联通讯技术的交通流跟驰模型 [J]. 物理学报, 2016, 65(1): 52-63. Hua Xuedong, Wang Wei, Wang Hao. A car-following model with the consideration of vehicle-to-vehicle communication technology [J]. Acta Physica Sinica, 2016, 65(1): 52-63. [24] 薛郁,董力耘,戴世强. 一种改进的一维元胞自动机交通流模型及减速概率的影响 [J]. 物理学报, 2001, 50(3): 445-449. Xue Yu, Dong Liyun, Dai Shiqiang. Model of traffic flow and the effect of deceleration probability [J]. Acta Physica Sinica, 2001, 50(3): 445-449. [25] 雷丽,薛郁,戴世强. 交通流的一维元胞自动机敏感驾驶模型 [J]. 物理学报, 2003, 52(9): 2121-2126. Lei Li, Xue Yu, Dai Shiqiang. One-dimensional sensitive driving cellular automaton model for traffic flow [J]. Acta Physica Sinica, 2003, 52(9): 2121-2126. [26] Fang Y, Chen J Z, Peng Z Y. The effect of moving bottlenecks on a two-lane traffic flow [J]. Chinese Physics B, 2013, 22(10): 108902. [27] Zheng Y Z, Zheng P J,Ge H X. An improved car-following model with consideration of the lateral effect and its feedback control research [J]. Chinese Physics B, 2014, 23(2): 020503. [28] Ling X, Hu M B, Jiang R, et al. Global dynamic routing for scale-free networks [J]. Physical Review E, 2010, 81(1): 016113. [29] Tang T Q, Huang H J, Wong S C, et al. A new car-following model with consideration of the traffic interruption probability [J]. Chinese Physics B, 2009, 18(3): 0975-0983. [30] 李树彬,吴建军,高自友, 等. 基于复杂网络的交通拥堵与传播动力学分析 [J]. 物理学报, 2011, 60(5): 050701. Li Shubing, Wu Jianjun, Gao Ziyou, et al. The analysis of traffic congestion and dynamic propagation properties based on complex network [J]. Acta Physica Sinica, 2011, 60(5): 050701. [31] Chang G, Park S Y, Paracha J. Intelligent transportation system field demonstration integration of variable speed limit control and travel time estimation for a recurrently congested highway [J]. Transportation Research Record: Journal of the Transportation Research Board, 2011, 2243: 55-66. [32] Chang G, Park S. Field evaluation of variable speed limit control for contending with recurrent highway congestion [R]. Maryland State Highway Research Report, 2010, MD-09-SP708B4B. [33] 王薇,杨兆升,赵丁选. 有限阶段马尔可夫决策的可变限速控制模型 [J]. 交通运输工程学报, 2011, 11(5): 109-114. Wang Wei, Yang Zhaosheng, Zhao Ddingxuan. Control model of variable speed limit based on finite horizon Markov decision-making [J]. Journal of Traffic and Transportation Engineering, 2011, 11(5): 109-114. [34] Abde-aty M, Cunningham R J, Gayah V V, et al. Dynamic variable speed limit strategies for real-time crash risk reduction on freeways [J]. Transportation Research Record, 2008, 2078: 108-116. [35] 蒲云,胡路,蒋阳升, 等. 高速公路主线收费站可变限速控制 [J]. 交通运输工程学报, 2012, 12(5): 119-126. Pu Yun, Hu Lu,J iang Yangsheng, et al. Variable speed-limit control before expressway mainline toll station [J]. Journal of Traffic and Transportation Engineering, 2012, 12(5): 119-126. [36] 张晶晶,庞明宝,任沙沙. 基于元胞自动机模型的高速公路可变速度限制交通流特性分析 [J]. 物理学报, 2012, 61(24): 244503-1-8. Zhang Jingjing, Pang Mingbao, Ren Shasha. Characteristic analysis of traffic flow in variable speed limit section of freeway based on cellular automaton model [J]. Acta Physica Sinica, 2012, 61(24): 244503-1-8. [37] 李树彬. 城市交通系统运行状态评估及控制策略研究 [D]. 北京:北京交通大学, 2012. Li Shubin. Research on the run state evaluation of urban transportation system and control strategies [D]. Beijing: Beijing Jiaotong University, 2012. [38] 谢东繁 基于微观模型的城市道路交通流若干典型问题研究 [D]. 北京:北京交通大学, 2010. Xie Dongfan. Analyzing of typical problems of urban road traffic flow based on microscopic models [D]. Beijing:Beijing Jiaotong University, 2010. [39] 王涛. 基于格子流力学模型的交通流建模及仿真研究 [D]. 北京:北京交通大学, 2015. Wang Tao. Research on traffic flow modeling and simulating based on the lattice hydrodynamic model [D]. Beijing:Beijing Jiaotong University, 2015. [40] Xie D F, Gao Z Y, Zhao X M. The effect of ACC vehicles to mixed traffc flow consisting of manual and ACC vehicles [J]. Chinese Physics B, 2008, 17(12): 4440-4445. [41] Jiang B,Claramunt C. Topological analysis of urban street networks [J]. Environment and Planning B, 2004, 31: 151-162. [42] Gao Z Y, Li K P, Li X G, et al. Scaling laws of the network traffic flow [J]. Physica A, 2007, 380: 577-584. [43] Wu J J, Gao Z Y,Sun H J. Urban transit system as a scale-free network [J]. Modern Physics Letters B, 2004, 18: 1043-1049. [44] Erdö s P, Ré nyi A. Publications of the mathematical institute of the hungarian academy of science [J]. Graph Theory, 1960, 5(1): 17-61. [45] 吴建军. 城市交通拓扑结构复杂性研究 [D]. 北京:北京交通大学, 2008. Wu Jianjun. Topological structure complexity of urban traffic research [D]. Beijing:Beijing Jiaotong University, 2008.
1.2 可变限制速度模型


1.3 基于可变限速的车辆移动模型
2 基于可变限速的中观交通仿真流程
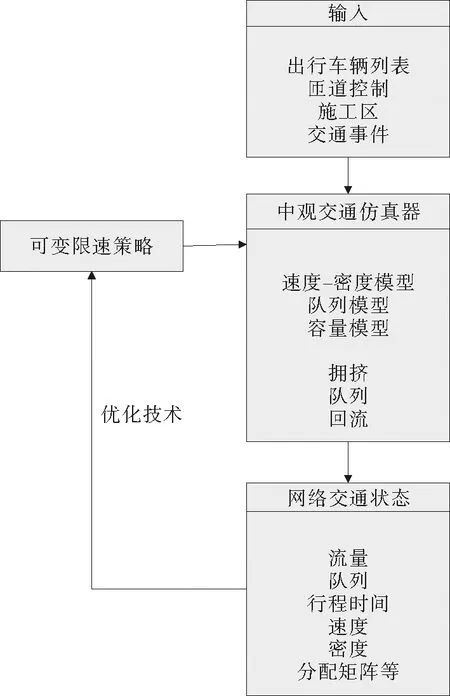
3 可变限速优化模型
ϑp(k,mp)p=1,2,…,P;k=1,2,…,K4 仿真研究
4.1 复杂交通网络拓扑的构建
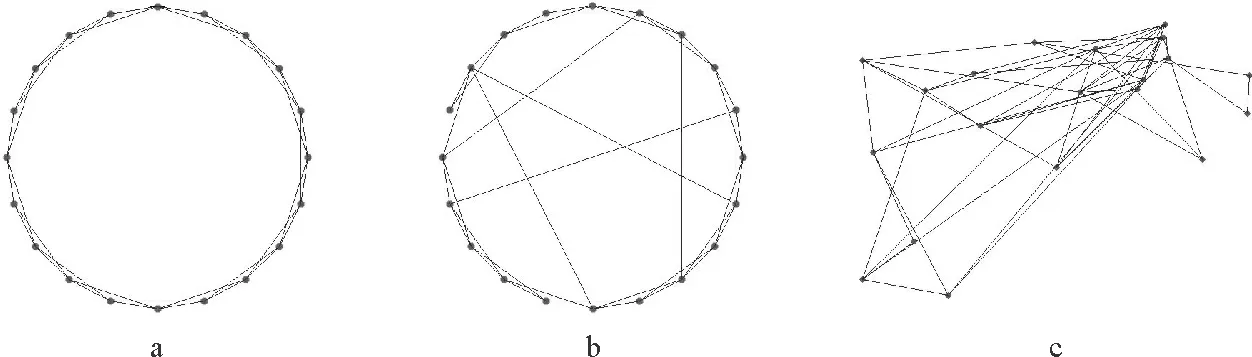
4.2 仿真环境
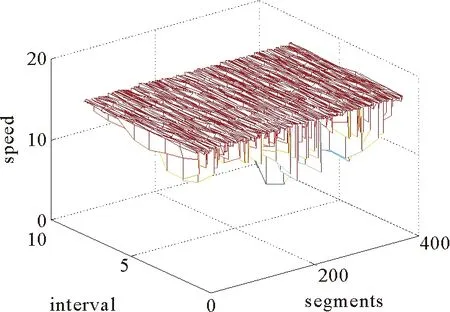
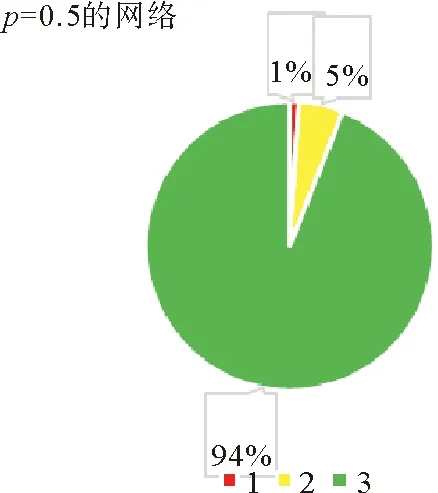
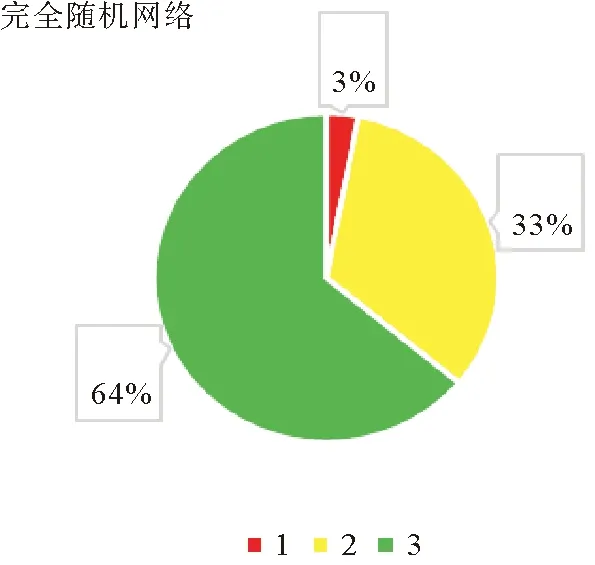
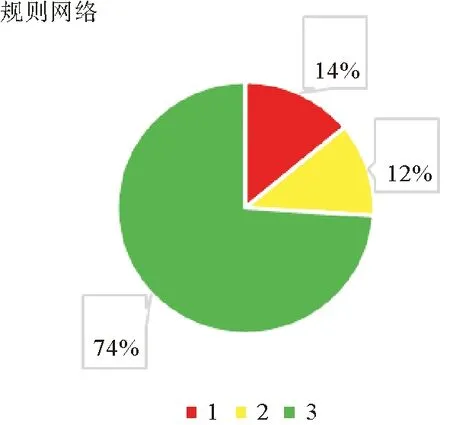
4.3 仿真结果以及分析


5 结论

