基于保证集的多智能体系统自触发控制
成 云,宋运忠
(河南理工大学电气工程与自动化学院,河南 焦作 454000)
0 引言
在信息物理系统的研究中,计算、通信与控制融合的重要性得到进一步重视[1-2]。为了确保网络化信息物理系统的运行效率,越来越多的工作投入到研究分布式控制器的设计和实时执行。近年来,多智能体系统控制的研究逐渐成为热点[3-10]。多智能体系统工作时,能耗与传感器采样、处理器重计算控制输入、执行器信号的传输和接收器侦听潜在输入信号的速率相关。周期性地[11]执行这些任务有时候是没有必要的。为了解决这些问题,相关学者提出了触发式控制,它的目的是找出一个标准以允许智能体调整控制器的执行和采样方案,从而完成系统的任务并达到期望的性能水平。在事件触发控制[12-18]中,关键点是查明网络执行中的事件,虽然减少了采样或控制器更新,但是大多需要全局的或邻居的连续可得信息,使得它的执行会受到较多外界因素的干扰。事件触发控制还有个根本的缺陷,即触发条件是被动检查的。参考文献[17]中探索了基于事件触发的分布式通讯和控制策略,在这一控制策略中,每个智能体有一个先验的局部误差容许范围,一旦超出了容许范围,此智能体就向邻居广播它的当前状态。而在自触发控制[19-21]中,只需依赖单个智能体的当前可得信息,这一特点使得自触发策略特别适合分布式控制器的执行。在参考文献[21]中,通过执行自触发通信方案实现了分布式控制,其中的一些智能体为自触发条件考虑了最保守的情况。
本文以保证集为基础,提出了一种新的自触发方法。因为保证集提供了大量关于智能体未来所有可能轨迹的信息,所以这一自触发方法有助于减小控制消耗等。
1 预备知识和问题描述
1.1 预备知识
R,R≥0分别表示实数集合和非负实数集合,‖·‖2表示向量的二范数。对于Ai∈Rmi×ni,其中i∈{1,…,N},本文用diag(A1,…,AN)∈Rm×n表示分块对角阵,其中
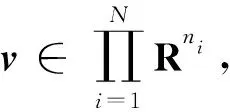
1.2 问题描述
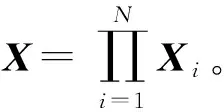
(1)
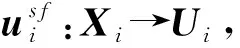

(2)
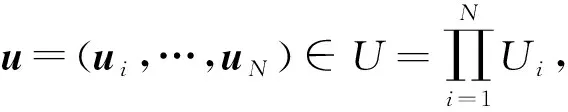

(3)

定义具有无向通信拓扑图G,动力学方程(3),同时满足公式(2)的智能体群体为一个网络化的信息物理系统。本文的目的是,找到一种控制协议使智能体群体汇聚到期望集合D中。假定存在一个连续的映射u*:X→U和一个有下确界的连续可微函数V:X→R(可以根据D的不同形式来设计相应的V(x)),使得期望集合D是极小化V之后的集合,且对于∀x∉D满足:
(4a)
(4b)
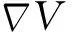
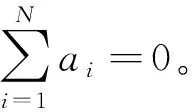
2 多智能体系统的自触发控制
从执行的角度看,控制器u*需要智能体间的连续通信及执行器信号的连续更新,这使得通信和执行的代价很高,因此并不适合实际情况。为了解决挑选请求信息的时刻这一问题,本文提出了一种新的自触发通信和控制策略。
2.1 自触发控制的理论基础
一般的思路是,在网络化信息物理系统(3)的状态演化过程中,保证李雅普诺夫函数V关于时间的全微分一直小于等于零,即使智能体所使用的信息是不精确的。
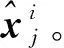
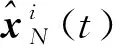
(5)
问题是,式(5)不仅需要全局信息,还无法用分布式的方法来检查。因此,本文定义了一个局部事件,即智能体i需要更新信息的时刻为
(6)

定义1(可达集) 在式(1)下,给定初始状态y∈Xi,从初始状态y出发,经过s秒的可达集为
其中,控制输入ui是个连续(时间)函数。可以看出,如果每个智能体都可以收到邻居的动力学方程和控制空间等信息,那么它就可以用这个公式构造出每个时刻可以获得的状态信息,且这一集合保证包含邻居的真实状态。

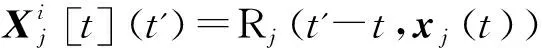
(7)

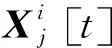
一般来说,计算出实际可达集或者保证集的代价很高。通用的方法是,通过凸多面体或椭球体来计算出一个关于实际可达集的过近似可达集[22-23]。再者,通过使用过近似可达集,智能体还可以处理无法获得邻居模型精确信息的情况。
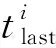
(8)
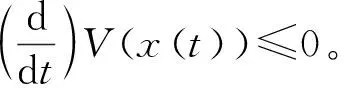
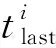
2.2 自触发控制的实现
前面介绍的自触发方法赋予了单个智能体自治的特性,这一特性可以用来查明在什么时间、需要什么样的信息。下面给出自触发控制的实现方法,包括集值信息模型下的控制器设计(一般意义上),以及对自触发信息的更新。
2.2.1 集值信息模型中的控制器设计
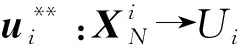
(9a)
(9b)

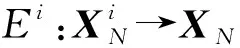
(10)
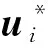

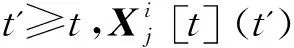
2.2.2 自触发信息的更新
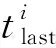
(11)

(12)
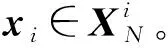
(13)
(14)

对于保证集来说,设定一个终止时间Texp>Td,self是合理的。即,保证集在t∈[tlast,tlast+Texp]时是有效的,而保证集的终止也会造成新的自触发更新。
2.2.3 自触法算法
在本文介绍的以上原理和设计的基础上,我们提出了一种自触发算法。
1)自触发信息的更新
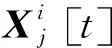
2)对请求的响应

2.3 自触发算法的收敛性
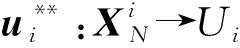
证明:在自触发算法下,函数V(x)关于时间是连续可微的或分段连续可微的。对其求全微分,可以得到:
(15)
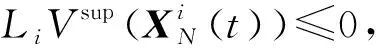
由以上证明可知,定理1是正确的。
3 仿真结果
用一个二维平面内多智能体运动控制问题来表明自触发方法的正确性。
在无向图G中,考虑4个智能体彼此通信,这个完整的拓扑图仅缺少了边(1,3)。期望集合D是一个长为2宽为1的矩形区域,其具体描述会在邻居智能体间的期望距离参数{dij}中给出。每个智能体都是独轮车模型,其动力学方程为
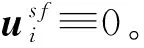
其中,dij是事先设定的智能体i和j之间的期望距离,而e(xj-xi)表示xj-xi方向上的单位向量。控制协议给定为
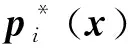

图1显示了自触发协议下所有智能体的运行轨迹。可以发现,所有的智能体都向着期望的矩形区域运动。
图2中显示了每个智能体自触发的时刻以及自触发的次数。
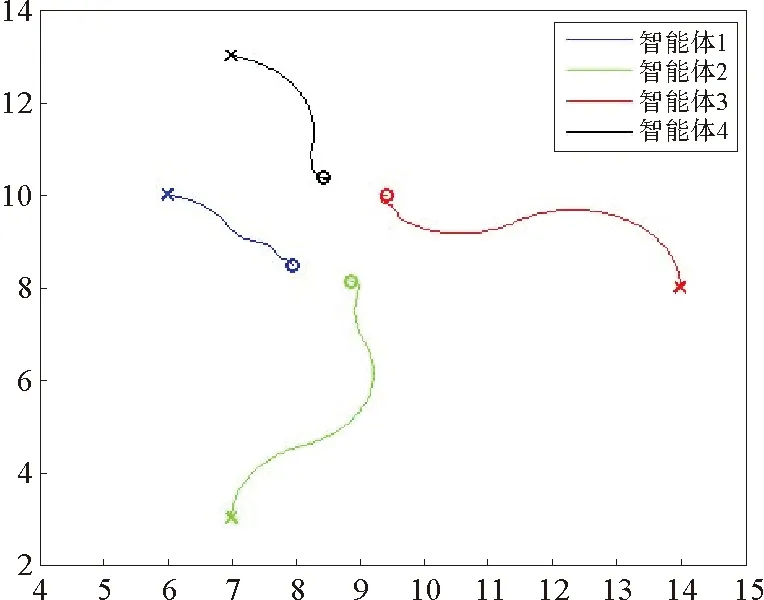
“x”和“o”分别表示每个智能体的初始状态和终止状态图1 执行自触发算法后的轨迹Fig.1 Trajectories of an execution of Self-Triggered algorithm
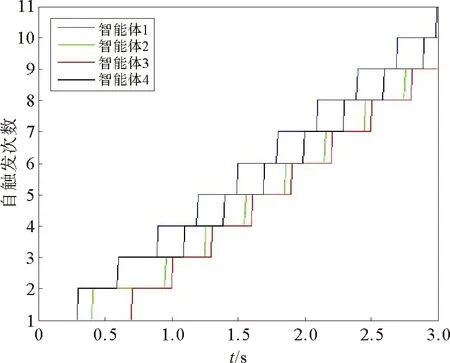
图2 每个智能体的自触发请求数量Fig.2 Number of self-triggered requests made by each agent
图3表明了自触发协议下的李雅普诺夫函数的演化是单调不增的,且减小速度较快。
图4中详细地显示了各个相邻智能体之间的距离随时间的变化。
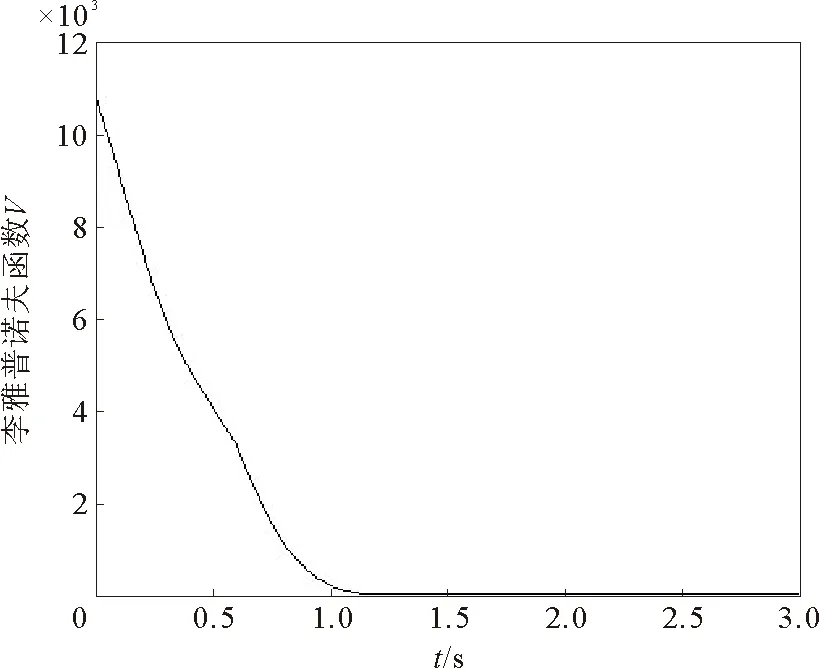
图3 李雅普诺夫函数V的演化Fig.3 The evolution of the Lyapunov function V
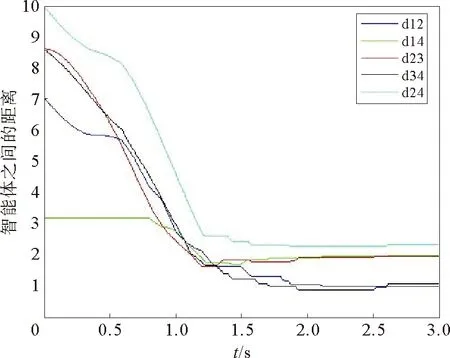
图4 相邻智能体之间的距离Fig.4 The distance between neighbor agents
4 结论
在保证集的基础上,本文为网络化信息物理系统中的分布式控制器的实时执行问题提供了一种新的解决方法,即自触发方法。在此方法下,智能体能够自治地安排请求信息及更新信息的时刻,不仅不需要邻居的连续状态信息,还降低了整体的执行消耗。一个多智能体系统汇聚控制的仿真结果验证了所提方法的正确性及有效性。本方法存在的问题是,随着智能体捕获邻居的所有可能轨迹,保证集会迅速变大,再加上智能体之间最终会过于接近,这些情况都会导致较保守的自触发执行。
[1]Kim K D, Kumar P R. Cyber-physical systems: a perspective at the centennial[J]. Proceedings of the IEEE, 2012, 100:1287-1308.
[2]Sztipanovits J, Koutsoukos X, Karsai G, et al. Toward a science of cyber-physical system integration[J]. Proceedings of the IEEE, 2012, 100(1):29-44.
[3]薛磊, 王庆领, 孙长银. 博弈论框架下的二阶多智能体系统领导者选择算法[J]. 控制理论与应用, 2016,33(12):1593-1602.
Xue Lei, Wang Qingling, Sun Changyin. Game theoretical approach for the leader selection of the second-order multi-agent system[J]. Control Theory & Applications, 2016, 33(12):1593-1602.
[4]金治群, 牛玉刚, 邹媛媛. 带有滑模观测器的多智能体一致性控制[J]. 控制理论与应用, 2017, 34(2):251-259.
Jin Zhiqun, Niu Yugang, Zou Yuanyuan. Consensus for multi-agent systems with sliding-mode observer[J]. Control Theory & Applications, 2017, 34(2):251-259.
[5]孙戎, 贾英民. 多智能体网络一致性鲁棒H∞控制问题[J]. 复杂系统与复杂性科学, 2012,9(1):16-22.
Sun Rong, Jia Yingmin. Robust H∞ control problem consensus of multi-agent network[J]. Complex Systems and Complexity Science, 2012,9(1):16-22.
[6]杨洪勇, 徐邦海, 刘飞, 等. 分数阶多智能体系统的时延一致性[J]. 复杂系统与复杂性科学, 2013, 10(3):81-85.
Yang Hongyong, Xu Banghai, Liu Fei, et al. Consensus of fractional-order multi-agent systems with communication delay[J]. Complex Systems and Complexity Science, 2013, 10(3):81-85.
[7]李勃, 陈增强, 刘忠信, 等. 含时延的多智能体系统的多静态领导者包容控制[J]. 复杂系统与复杂性科学, 2016, 13(2):105-110.
Li Bo, Chen Zengqiang, Liu Zhongxin, et al. Containment control for multi-agent system with multiple stationary leaders and time-delays[J]. Complex Systems and Complexity Science, 2016, 13(2):105-110.
[8]宋运忠, 赵威. 基于群体社会制度策略的主从多智能体汇聚[J]. 复杂系统与复杂性科学, 2012, 9(1):88-94.
Song Yunzhong, Zhao Wei. Leader follower multi-agents network rendezvous via swarm social system strategies[J]. Complex Systems and Complexity Science, 2012, 9(1):88-94.
[9]窦全胜, 刘柏枫, 厉玉蓉, 等. 线性均方一致性问题的偏差估计[J]. 自动化学报, 2017, 43(4):568-575.
Dou Quansheng, Liu Baifeng, Liu Yurong, et al. Variance estimation for linear mean square consensus problem[J]. Acta Automatica Sinica, 2017, 43(4):568-575.
[10] 李宗刚, 谢广明, 高溥. 一类线性多智能体系统输出反馈H∞包围控制[J]. 复杂系统与复杂性科学, 2013, 10(3):86-94.
Li Zonggang, Xie Guangming, Gao Pu. Output feedback H∞ containment control of linear multi-agent system[J]. Complex Systems and Complexity Science, 2013, 10(3):86-94.
[11] Hristu-Varsakelis D, Levine W S, Alur R, et al. Handbook of Networked and Embedded Control Systems (Control Engineering)[M]. Birkhäuser Boston, 2005.
[12] Tabuada P. Event-triggered real-time scheduling of stabilizing control tasks[J]. IEEE Transactions on Automatic Control, 2007, 52(9):1680-1685.
[13] Donkers M C F, Heemels W P M H. Output-based event-triggered control with guaranteed L∞-gain and improved and decentralized event-triggering[J]. IEEE Transactions on Automatic Control, 2012, 57(6):1362-1376.
[14] Dimarogonas D V, Frazzoli E, Johansson K H. Distributed event-triggered control for multi-agent systems[J]. IEEE Transactions on Automatic Control, 2012,57(5):1291 - 1297.
[15] Garcia E, Antsaklis P J. Model-based event-triggered control for systems with quantization and time-varying network delays[J]. IEEE Transactions on Automatic Control, 2013, 58(2):422-434.
[16] Heemels W P M H, Donkers M C F. Model-based periodic event-triggered control for linear systems [J]. Automatica, 2013, 49(3):698-711.
[17] Wang X, Lemmon M D. Event-triggered broadcasting across distributed networked control systems[C]// American Control Conference, IEEE, 2008:3139-3144.
[18] 杨若涵, 张皓, 严怀成. 基于事件触发的拓扑切换异构多智能体协同输出调节[J].自动化学报, 2017, 43(3):472-477.
Yang Ruohan, Zhang Hao, Yan Huaicheng. Event-triggered cooperative output regulation of heterogeneous multi-agent systems with switching topology[J]. Acta Automatica Sinica, 2017, 43(3):472-477.
[19] Velasco M, Mart P, Fuertes J M. The self triggered task model for real-time control systems[C]∥ 24th IEEE Real-Time Systems Symposium, 2004:67-70.
[20] Anta A, Tabuada P. To sample or not to sample: self-triggered control for nonlinear systems[J]. IEEE Transactions on Automatic Control, 2010, 55(9):2030-2042.
[21] Nowzari C S J. Self-triggered coordination of robotic networks for optimal deployment[J]. Automatica, 2012, 48(6):1077-1087.
[22] Althoff M, Guernic C L, Krogh B H. Reachable set computation for uncertain time-varying linear systems[C]// ACM International Conference on Hybrid Systems: Computation and Control, Chicago, 2011:93-102.
[23] Frehse G. PHAVer: Algorithmic verification of hybrid systems past HyTech[J]. International Journal on Software Tools for Technology Transfer, 2008,10(3):263-279.
[24] Blanchini F, Miani S. Set-Theoretic Methods in Control[M]. Boston: Birkhäuser Boston, 2008.

