两层星型网络上的传染病建模和控制
郑国庆,唐清干,祝光湖
(桂林电子科技大学数学与计算科学学院,桂林 541004)
0 引言
传染病数学模型可以追溯到1927年Kermack与McKendrick创立的“仓室模型”,至今仍在广泛应用,并被不断发展和推广[1-2]。传染病模型能够描绘疾病的传播过程,解释疾病的流行因素,并为疾病的防治工作给予理论指导[1]。模型中仓室结构以及个体在仓室的转移由具体疾病决定,考虑不同的疾病和传播方式,现已建立了非常多的传染病模型[1-2]。经典的有SIS和SIR模型,如在SIS模型中,所有个体将会被分成两类:S-易感者(Susceptibles)和I-染病者(Infected)。易感者被感染者感染后可以恢复,但不具备免疫力。模型用常微分方程描述如下:

其中β=pC(N)表示传染率,γ表示恢复率,C(N)是接触率,p表示每次接触的传染概率。传统模型假设群体是均匀混合,个体间的接触机会相等,如上式中C和β,这种假设往往无法体现个体的异质性,相应的模型往往不够准确。而新兴的复杂网络理论为传染病模型的构建提供了很好的工具,能够更精确地描述传播过程[3-4]。
从20世纪末开始,复杂网络研究逐步渗透到数理、生命和工程等众多不同的领域,并获得了很多开创性的成果[3-16]。在众多的网络结构中,星型网络是一种典型的规则网络,由一个中心节点和多个边界点构成,每一个边界点都与中心节点相连,但边界点之间不连接,如图1a所示。如局域网,内部所有个人计算机与一个总服务器相连,形成以总服务器为中心的一个星型网络。星型网络也可推广到多个中心的情形,如在社会网络中以少数人为中心的社区或单位[4]。最近研究表明系统都不是孤立存在的,因而由不同子网相互作用构成的耦合网络更能准确地刻画真实系统,如交通网络和计算机网络等[4-6]。本文将把单层星型网络推广到两层星型耦合网络,如图1b所示。这是一类特色的社团结构,特别的,在中心城市及其周边县城构成的交通系统中,如果把两个中心城看成是中心节点,周边县城看出边缘节点,而忽略交通量较少的县城连接,则此系统可用两层星型耦合网络表示。研究此网络上的传播能够揭示疾病在中心和周边地区传播扩散的规律并获得有效的防控策略。现实生活也有类似案例,如2003年非典先从中国经济繁荣、人口流动性大的广州和北京这两个中心城市开始蔓延至周边地区,之后引起大范围的扩散。

图1 两种星型网络两层星际网络由两个单层星型模型构成,两个中心节相连,每层中的边界点除了与该层的中心节点相连还与另一层中对应的边界点相连。
传染病的防控策略主要有3种:控制感染源、切断传播途径和保护感染者,具体有隔离和接种等。例如在非典全面爆发时期,政府将被感染者和疑似感染者进行隔离,对所有单位和学校等公共场所定期消毒,并号召人们出行带着口罩。这些措施有效减轻了SARS病毒扩散。另外,疫苗可以刺激机体产生抗体,通过提高对病毒的免疫力来预防疾病,进而减少疾病传播的范围。世界卫生组织的数据显示,通过接种全球麻疹死亡人数从2000年的54.4万例下降到2013年的14.5万例,降幅约75%。最近针对复杂网络结构特点,人们提出了几类有效的免疫策略,如熟人免疫、目标免疫和主动免疫等[7-9]。研究发现网络的异质性和个体行为的自适应性很大程度上左右着疾病的传播和控制[3,7-10],因此研究特定网络上的传染病扩散和防控有着实际意义。
本文利用Jennifer等人提出的有效度模型[11-12],研究两层星型网络上疾病的传播,探索有效的疾病控制策略。下一节我们给出刻画模型的常微分方程组。第3节我们采用The next generation matrix方法分析疾病的基本再生数。第4节我们介绍两种防控疾病的方法:截断传播途径和对易感者免疫。第5节中,我们利用Matlab分别对两种防控方法做数值模拟,通过依次改变传染率,群体规模和易感者的初值比较两种方法的优劣性。最后我们对结果进行分析与讨论。
1 有效度模型
有效度模型是由Jennifer等人于2010年提出的一种新的网络传染病的建模思想[11-13]。与传统的平均场模型相比,它不仅将所有节点根据状态分为易感者或感染者,而且还记录了相连的邻居个数和状态,例如用Ssi表示具有s个易感邻居和i个感染邻居的易感节点数量;如果一个Ssi类节点被它的i个感染邻居中的某个感染,则从Ssi类变为Isi类节点,节点状态发生了变化;如果一个Ssi类节点的i个感染邻居中某个恢复,节点就会从Ssi类变为Ss+1,i-1类;如果某个Ssi类节点的s个易感邻居中某个被感染,节点就从Ssi类变为Ss-1,i+1类。
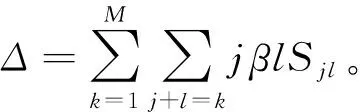
由此静态网络上SIS有效度模型可表示为[13]:
(1)
(2)

根据上述模型,本文分析两层星型网络传染病的有效度模型的常微分系统。假设每层边界点的个数为n,中心点个数为1,恢复率γ=1。对于边界点,它的度是2,即k=s+i=2。对应的有效度模型为

而对于中心节点,它的度是n+1,即k=s+i=n+1,有效度模型为
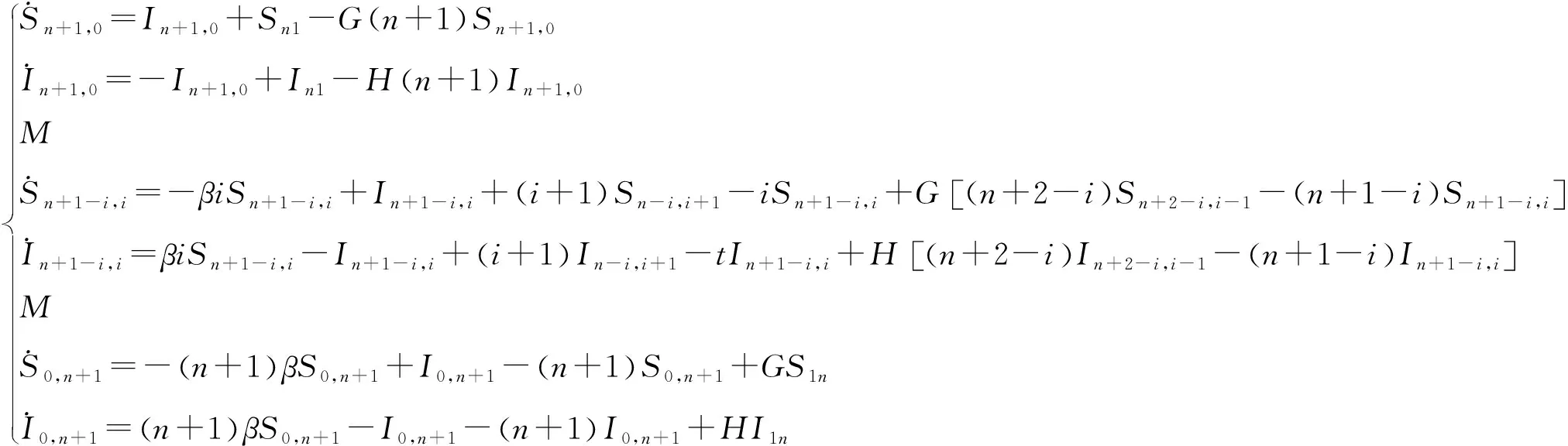
其中,0≤t≤n+1,G=Δ/Λ,H=Φ/Ψ。
2 基本再生数
在传染病动力学研究中,基本再生数是一个十分重要的概念。假设群体中的所有个体均是易感者,此时一个感染者在平均患病期内所感染的人数就定义为基本再生数[1,2,14],一般用R0表示。如果R0<1,则一个染病者在其患病期间感染人数不足一个,疾病将会迅速消亡;相反如果R0>1,则疾病会始终存在并形成地方病。因此为了防止疾病的流行,必须采取相应的方法尽量减少R0。通常用R0=1作为决定疾病是否消亡的阈值。
有效度模型(1)和(2)满足平衡条件,即所有易感节点的感染邻居总数和所有感染节点的易感邻居总数均等于所有连接易感节点和感染节点边的总数[11]:
(3)
根据式(3),方程(2)可以改写成:
(4)
在无病平衡点附近,感染节点的数量很少,一个易感节点的感染邻居数量多于1的情况不大可能,即对一切i>1,Ssi≈0。则有:
因此在无病平衡点附近有:
(5)
下面采用The next generation matrix方法来计算模型的基本再生数R0。将(1)和(5)在无病平衡点处线性化,其雅克比矩阵写成F-V的形式,其中F矩阵表示疾病生成项。V矩阵表示转移项[14]。对于一个固定的度k(1≤k≤M),(1)和(5)可以写成2(k+1)个方程,但由于Sk0是全易感类,没有机会接触染病者,这类方程可以忽略,这样需要考虑的方程共有2k+1个。
根据Jennifer等人的研究[11,13],矩阵F的表达式为
(6)
其中,uk和vk都是2(k+1)×1的向量。uk的第一个元素是kSk0,其它元素都是0。而vk的前k-1个元素分别是k-1,2(k-2),…,t(k-t),…,k-1,其余元素均为0。这里F是一个M(M+2)阶矩阵,对它进行初等变换可知道矩阵F的秩是1。


根据上面的方程可写出矩阵V2:
O.Diekmann等人用谱半径ρ来表示基本再生数R0=ρ(FV-1),ρ(A)表示矩阵A的谱半径,即矩阵A的最大特征值的绝对值[16]。有效度模型的基本再生数可以表示为[13]:
(7)
根据式(7),两层星型网络传染病的有效度模型的基本再生数可表示为
3 防控策略
为了控制疾病扩散,我们应该采取一些防控策略来降低基本再生数。这里我们介绍两种最常见的方法。第一种是控制感染源,切断传播途径,如禽流感病毒爆发时,应尽可能的减少与家禽的直接接触;第二种是保护易感者,对易感者接种疫苗,使其对病毒具有免疫能力。
3.1 切断连边
假设两层星型网络中每层边界点的个数为n,中心点个数为1。采取每种方法都会有3种不同的方案。我们先考虑第一种方法——切断传播路径,即断边,有下面3类实施方案。
1)切断两个边界点之间的边,如图2a所示。假设选择10%的边断开,此时模型中有3类节点,分别是度为1的节点,度为2的节点以及度为n+1的中心节点。根据(7)式,基本再生数可表示为

图2 切断传播路径的3种方案
2)切断边界点与中心点之间的边,如图2b所示。假设上下各选择10%的边断开,此时模型中有3类节点,分别是度为1和度为2的的边界点以及度为(0.9n+1)的中心点。根据式(7),基本再生数为
3)切断两个中心点之间的边,如图2c所示。此时模型中有两类节点,分别是度为2的边界点以及度为n的中心点。那么基本再生数为:
3.2 免疫节点
考虑第二种方法防控方法,即免疫节点,同样也有三种实施方案。

图3 免疫节点的3种实施方案
1)随机选择一些易感的边界点,对其进行免疫,如图3a所示。假设上下各选择10%的易感边界点进行免疫,则此时模型中有3类节点,分别是度为1和度为2的边界点以及度为(0.9n+1)的中心点。此时的基本再生数为:
2)免疫其中一个中心点,如图3b所示。则此时模型中有3类节点,分别是度为1点和度为2的边界点以及度为n的中心点。此时的基本再生数:
3)对两个中心点都免疫,如图3c所示。则此时模型中只有度为1的节点。此时的基本再生数为:
4 数值分析
我们已经计算了各种控制方案的基本再生数,为了揭示模型参数对传播过程的影响,从而出最佳的疾病控制方案,下面我们利用Matlab软件模拟传播模型与断边和免疫的3种方案的基本再生数R0随感染率β、S20的初值、边界点规模n变化的曲线图。下面假设γ=1,初始时刻有一个中心节点被感染。
4.1 切断连边的效果分析
图4表示在不同的参数条件下,切断连边对基本再生数的影响。左图表明基本再生数与感染率是成正比,因此降低感染率能有效地减少疾病的传播;中图表明基本再生数与S20的初值变化是成反比的关系,说明网络中易感节点越多疾病越不容易传播;右图表明基本再生数与边界点规模是成正比,因此减少边界点的规模能有效降低疾病的传播。总而言之,切断途径的3种方案的曲线都能降低基本再生数,但第1种方案(切断10%边界连边)效果不理想,而若只切断中心节点之间的一条边,效果也一般,第2种方案(切断10%边界与中心的连边)效果最佳。

图4 在不同的情况下,切断连边对基本再生数R0的影响Fig.4 The effects of disconnecting links on the basic reproduction number R0in case of different situations
4.2 免疫节点的效果分析
图4表示在不同的参数条件下,免疫节点对基本再生数的影响。结果发现免疫的3种方案都能有效地降低基本再生数。其中第2种方案(免疫一个中心节点)效果最差,第3种方案(免疫两个中心节点)效果最佳,基本能达到将基本再生数控制在0的附近,使疾病彻底消除。

图5 在不同的情况下,免疫节点对基本再生数R0的影响Fig.5 The effects of vaccinating nodes on the basic reproduction numberR0in case of different situations
从图5也可以看出免疫10%的边界点比免疫其中一个中心节点更有效。下面我们通过改变接受免疫的边界点数量,分析免疫边界点和一个中心节点的等效性,结果如图6所示。我们发现将接受免疫的边界点数量设定为1%时,两种方案的基本再生数曲线基本重合;当免疫的边界点越多,控制效果就会越好。由此可知,当网络规模很大时,免疫中心节点即有效又经济,而且规模越大,效果越明显。

β=0.03,S10(0)=0.01n,S20(0)=0.5n图6 免疫边界点与中心点的比较
5 结论
本文运用复杂网络和传染病动力学理论研究了传染病在两层星型网络上传播动力性。首先利用SIS有效度模型将个体根据其邻居的状态进行分类,从而细化了传播过程。接着根据The next generation matrix方法分析了模型的基本再生数。为了降低基本再生数从而控制疾病的传播,我们提出了切断传播途径和免疫个体两种方法,根据不同情况又将其各自细分为3种不同的实施方案,并求出相应的基本再生数。最后我们利用Matlab数值分析,获得了两层星型网络上参数对疾病的传播影响以及有效的控制方案。
研究表明基本再生数与感染率和边界点规模成正比,降低感染率或边界点规模都能有效的减少疾病的传播;基本再生数与易感者的初值规模成反比,网络中初始时刻感染者越多会使疾病迅速扩散。这说明两层星型网络的特殊结构对疫情传播有直接影响,那些与感染者有直接接触的易感者会很容易被感染,而且网络节点数越多疾病传播越迅猛。我们还发现在两层星型模型中,我们提出的六种防控方案都能降低基本再生数,但是通过比较可以看出切断部分边界点与中心点的接触途径以及免疫两个中心点对疾病控制最有效。因此我们在疾病防控时要重点关注那些活动频繁和度大的节点,将这些点隔离或者免疫能大大降低传染病对社会财产和人们生命安全的威胁。
本文结果是基于静态网络上的疾病传播,适用于传播速度相对于群体结构变化快得多的情况。我们设定的两层星型模型中心节点上下各一个,但在现实中,一个群体内的中心节点或许有多个,这样网络结构就会变得复杂多变。如何将我们的理论研究贴近实际情况,解决现实问题是我们今后研究的动力和方向。
[1]马知恩,周义仓,王稳地,等.传染病动力学的数学建模与研究[M].北京:科学出版社,2004.
[2]Diekmann O, Heesterbeek J A P. Mathematical epidemiology of infectious diseases: model building, analysis, and interpretation [M]. New York: Wiley, 2000.
[3]Read J M, Keeling M J. Disease evolution on networks: the role of contact structure [J]. Proc R Soc Lond B, 2003, 270: 699-708.
[4]汪小帆,李翔,陈关荣.网络科学导论[M].北京:高等教育出版社,2012.
[5]Newmann M E J. The structure and function of complex networks [J]. SIAM Rev, 2003, 45: 167-256.
[6]Gao J, Buldyrev S V, Stanley H E, Havlin S. Networks formed from interdependent networks [J]. Nature Phys, 2012, 8: 40-48.
[7]Cohen R, Havlin S, et al. Efficient immunization strategies for computer networks and populations [J]. Phys Rev Lett, 2003, 91(24): 247901.
[8]王琴,祝光湖,傅新楚.有向网络上流行病阈值比较和免疫分析[J].复杂系统与复杂性科学, 2012, 9(4): 26-33.
Wang Qin, Zhu Guanghu, Fu Xinchu. Comparison of epidemic thresholds on directed networks and immunization analysis [J]. Complex Systems and Complexity Science, 2002, 9(4): 26-33.
[9]Fu X C, Michael S, et al. Epidemic dynamics on scale-free networks with piecewise linear infectivity and immunization [J]. Phys Rev E, 2008, 77: 036113.
[10] 王阳阳,阚佳倩,张海峰.个体的多策略行为不利于控制疾病传播[J].复杂系统与复杂性科学, 2015, 12(3): 14-18.
Wang Yangyang, Kan Jiaqian, Zhang Haifeng. Individuals' multi-strategy behavior is not conducive to control the spread of epidemic [J]. Complex Systems and Complexity Science, 2015, 12 (3):14-18.
[11] Jennifer L, Ma J, P van den D, et al. Effective degree network disease models [J]. Mathematical Biology, 2011, 62:143-164.
[12] Ma J, Pvan den D, Frederick H W. Effective degree household network disease model [J]. Mathematical Biology, 2013, 66: 75-94.
[13] 郑国庆,唐清干,祝光湖.带接种免疫的网络传染病的有效度模型[J].数学的实践与认识,2015, 45(15): 315-322.
Zheng Guoqing, Tang Qingan, Zhu Guanghu. An effective degree epidemic model with vaccination on networks [J]. Mathematics in Practice and Theory, 2015, 45(15): 315-322.
[14] Pvan den D, James W. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission [J]. Mathematical Biosciences, 2002, 180: 29-48.

