人体手部运动的振荡共振辅助系统实验研究

张 立，孙华通，潘园园，段法兵

(青岛大学复杂性科学研究所，山东 青岛 266071)

0 引言

以人体为研究对象，对其进行运动学和动力学分析的人体动力学，是一门基础理论学科[1-2]，已在航空、汽车等领域得到了广泛应用，对于机电产品设计以及虚拟现实研究具有重要意义。近年来，经济的发展使得人类分工精细，生活节奏明显加快，各种劳动损失不断出现，这些因素使得人体手部神经系统对外界感知灵敏度降低，也造成大量的人体运动障碍患者，社会对人体运动功能康复的需求越来越旺盛，逐渐形成了人体运动康复医学工程方向[1-2]。目前以生物力学和解剖学为基础，人体运动康复仅仅注重了运动原理的研究，对于神经系统中随机因素作用的研究较少。

生物神经系统中很多实验证实，普遍存在的随机干扰对于生物信息的传输是必要因素[3-5]，比如小龙虾，蟾蜍和白鼠的机械性刺激感受器[6-8]在适宜的噪声水平下敏感性最佳，这就是神经系统中的随机共振现象[3-8]。人体运动响应更是一个复杂的非线性系统，对低于自身阈值的输入做出反应时，“非信号”随机干扰往往能够起到有益的作用。Kurita等[9]提出利用随机共振现象增强人体触觉感知能力，他们通过触觉运动能力的手术钳抓握实验，证明了输入噪声水平保持在一定范围内可以提高手部触觉灵敏度；Kaut等[10]测试了随机全身振动能帮助提高帕金森病人的运动能力；Hur等[11]通过测试脉冲噪声作用于肌肉，观察肌肉对外界扰动的反应时间，得出使用振动脉冲噪声会增加人们对潜在危险情况的快速响应能力；Rogan等[12]进行了随机共振现象对老年人静态和动态平衡性以及反应时间的可行性双盲实验，得出未经训练的老年人经过随机共振效应训练后，能够提高其平衡和反应时间。王康康等[13-15]发现乘法噪声，加性噪声，关联噪声和时间延迟对生物系统中的随机共振现象有复杂的影响，并且影响系统稳定性。

随机共振辅助人体运动的系统需要伪噪声信号源刺激人体感知部位，实际操作中这种随机信号源的类型与强度调谐是非常困难的。Landa和McClintock[16]发现高频振荡信号和随机噪声的作用是类似的，若非线性系统中的内部噪声替换为确定性高频信号，则系统性能同样能够在某一适宜的振荡强度下出现共振现象，即振荡共振。高频振荡信号的易实现性和某些电子设备中固有的高频振荡源使得振荡共振的研究成为热点[16-18]。如任昱昊等[16-17]利用电路仿真证实了硬限幅并联系统中振荡共振原理的可实现性；Ullner等[19]发现了激振系统中振荡共振现象，表明最佳幅度的高频振动提高了激振系统对低频信号的响应。

目前为止，还没有对振荡共振机理增强人体运动能力的研究。与随机共振机理类似，振荡共振在生物医学功能恢复治疗方面也具有重要的实际应用价值。本文设计了一套基于振荡共振原理的人体手部运动辅助系统，系统的高频振荡源是由多个微电机组成的，将不同振动强度的振荡信号作用于手背部。通过改变振荡共振的振幅和频率，探究振荡共振原理对手部运动瞬时稳定性和整体相关性的影响。实验结果表明振荡共振辅助系统能够增强手部运动的稳定性，为人体医学康复仪器设计和制作提供了很好的生理实验基础。

1 实验方法

1.1 实验系统

图1显示了作用于手背部的振荡共振辅助系统：振荡源由STM32F103ZET6控制的微电机阵列产生。利用STM32F103ZET6的脉冲宽度调制功能[20]给微电机不同的驱动电压，通过改变驱动电压使微电机的频率和振幅得到改变，从而改变它的振动强度。选取电机阵列中一个微电机作为实例：得到电压与频率关系如图2所示，频率随电压的增大而增高。使用测振仪UT-315测试记录得到微电机幅值随电压变化的情况如图3所示，电压与振幅呈现非线性变化关系，这是由微电机的物理特性决定的。实验中将不同的微电机振动强度作用于手背部，分析探究振荡共振原理对手部运动平稳性的影响。

实验过程的工作视图如图4所示。实验者站立在白色面板前固定距离处，摄像头固定在白色面板和实验者之间。实验者手持激光笔，使激光沿着白色面板上的一条标定直线运动。利用面板前的摄像头捕捉激光沿着面板标定直线运动的轨迹，通过激光运动的轨迹，可以定量地计算手部运动的稳定性情况。

图1 振荡共振辅助系统Fig.1 Vibration resonance aided system

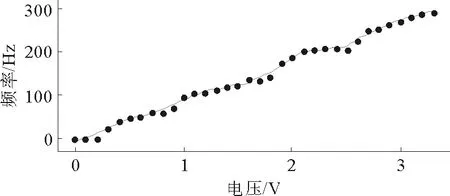
图2 微电机频率与电压关系

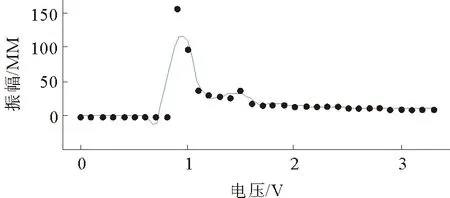
图3 微电机振幅与电压关系

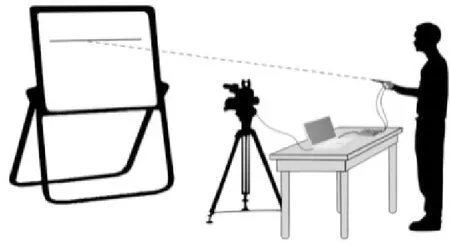
图4 系统工作图

1.2 实验条件

在单个微电机作为高频振荡源的情况下，采集了33级不同振动强度下手持激光笔的运动数据。分析数据得出以下实验条件：每次实验在20s-27s间完成，不在该时间段完成的实验数据不计入实验结果；在实验过程中，胳膊离身体外侧一定的距离，避免因身体支撑带来的实验误差；实验人员需保持正常呼吸；每8-10次实验为一组，避免身体疲惫造成的晃动方差变大。同时，在测试期间，一旦实验者对外部高频振荡源有任何不适，则立即停止实验。

1.3 测试方案

实验分别测试不同的微电机个数和不同的振动强度改善手部平稳性情况。将微电机个数作为组间因子，振动强度作为组内因子。依据微电机个数将实验分为4组(1个、2个、3个和4个)。实验表明，手背部的肌肉感知功能区域内，手背部微电机的放置位置对实验结果没有影响。每组选取了6级有特点的振动强度：0级时没有微电机的作用，1级时手部觉察不到微电机的作用，2级时手部能察觉到微电机轻微的振动，3级时手部能感觉到微电机明显的振动，4级时手部能察觉到微电机强烈的振动，5级为最大振动强度。施加电压与振动强度对应关系如表1所示。

表1 施加电压与振动强度对应关系Tab.1 Correspondence between voltage and vibration intensity

2 实验结果

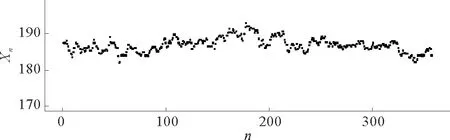
图5 特征点时间序列

使用Opencv库中VideoWriter类的write方法将摄像头捕捉到的图像写入视频文件，设置图像分辨率640×480，捕捉帧率25fps，那么特征点的采样间隔Δt=40ms，记一个像素宽度为Δs。每帧图像上的激光点称为特征点且唯一存在。处理数据时，首先使用Opencv的VideoCapture类的get方法获取视频文件的每帧图像，用SimpleBlobDetector特征检测器提取每帧图像特征点的纵坐标[21-22]。所有特征采样点按时间先后组成离散序列Xn，序列长度为N。例如，微电机个数为1，振动强度为2级时采集到的时间序列Xn如图5所示。

根据时间序列Xn，估计手部运动轨迹的均值和方差分别为[23]

(1)

(2)

运动轨迹的方差反映了手部运动过程的瞬时变化，D(X)越小，手部运动的瞬时稳定性越强。

为了测量长时间手部运动的整体相关性，时间相关函数Rm定义为[24]

(3)

其中，Xk和Xk+m是Xn在k和k+m的取值，k=1,2,…,N，m=1,2,…,N-k。定义相关时间τ=hΔt,h=1,2,…,N[24]，τ实际中由式(4)计算

R(τ)≤0.05R(0)

(4)

也就是取R(τ)=0.05R(0)的时间间隔τ。对于不同的离散时间序列，在R(τ)相等的情况下，τ数值越大，手部整体相关性越好。

不同的微电机个数以及振动强度的实验方差如图6和图7所示。由图6可知，在同等振动强度下，随着微电机个数的增加，D(X)总体呈现下降的趋势，但是分布不均匀。噪声水平为0级时，D(X)无明显变化。振动强度为2级时，D(X)变化比较明显，说明振动强度微弱的情况，不同的振动微个数对手部运动瞬时稳定性影响很大。振动强度为3级和4级时，D(X)变化幅值较小，说明在手部明显感知到外部振动的情况下，微电机个数对手部运动瞬时稳定性影响较小。图7显示了在微电机个数相同时，不同的振动强度对D(X)的影响。微电机个数相同时，随着振动强度的增大，D(X)呈现先下降后上升的趋势。当3个微电机同时作用时，这种趋势尤为明显。

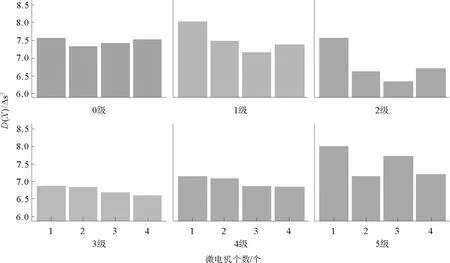
图6 同等振动强度下方差随微电机个数变化情况

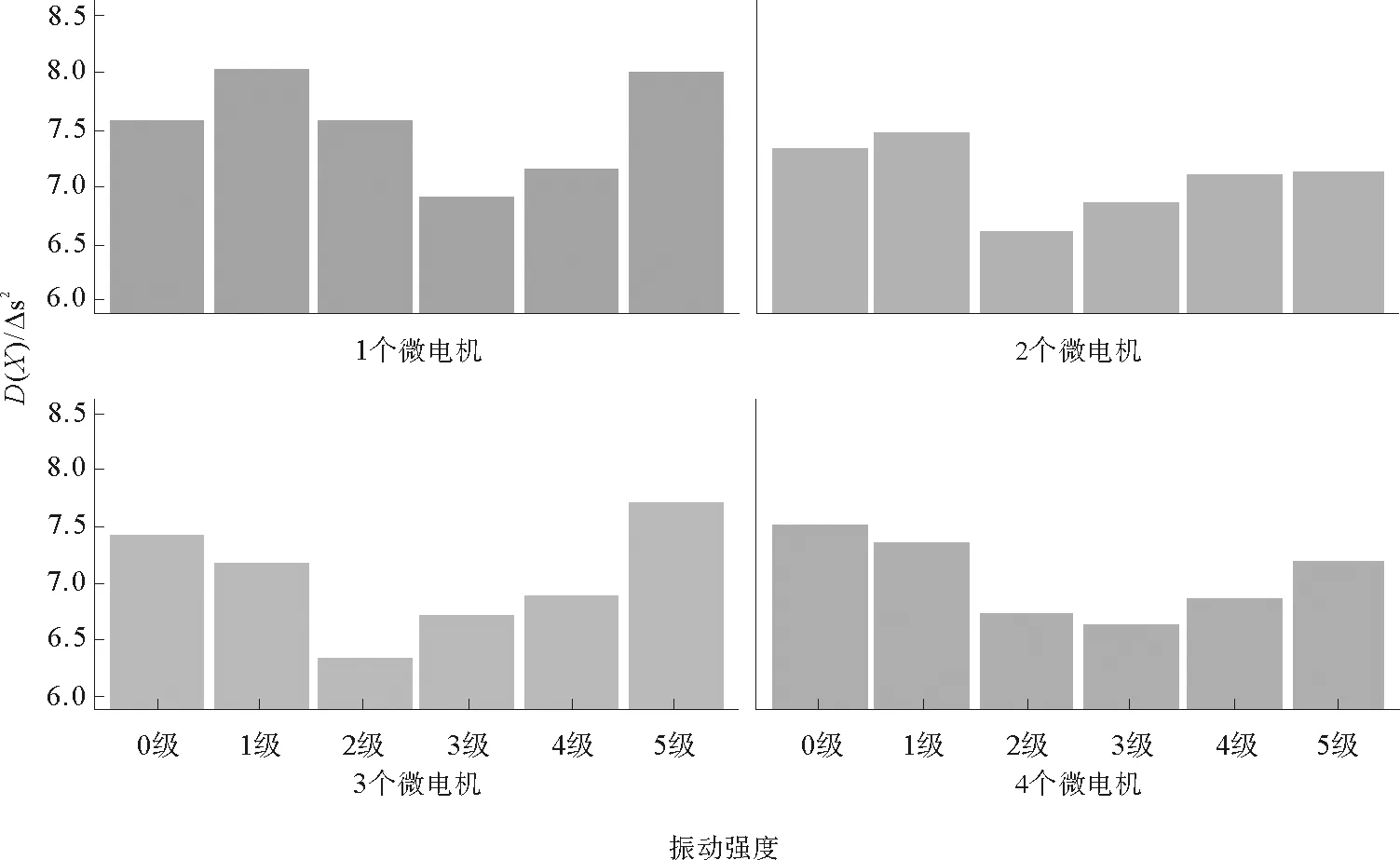
图7 相同微电机个数下方差随振动强度变化情况

为了探究手部运动瞬时稳定性的改善情况，定义比值ηi

(5)

这里,Di(Y)表示振动强度为i级时的方差值，i=1,2,3,4,5。计算ηi得到相同微电机个数作用下方差随振动强度变化表2。

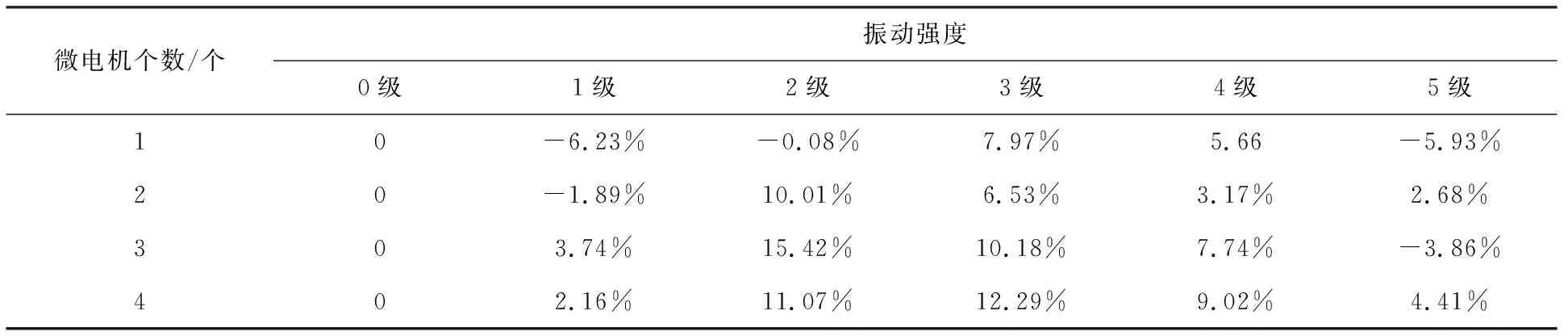
表2 相同微电机个数下方差随振动强度变化表Tab.2 Change of variance with vibration intensity for the same number of micro-motors

从表3中可以直观地看出微电机个数和不同振动强度对D(X)的影响。微电机个数为3，振动强度为2级时，D(X)减小15.42%，激光相对直线瞬时偏离程度最小，手部运动的瞬时稳定性最好；在振动强度为3级和4级时，D(X)均变小，手部运动瞬时稳定性均得到改善。可以得出使用振荡共振原理能够提高手部运动的瞬时稳定性。

图8展示了相同振动强度下，微电机个数对τ的影响。随着微电机个数的增加，τ总体上呈现上升的趋势。其中在振动强度为2级时，这种变化趋势尤其明显，说明同等振动强度下，微电机个数越多，手部运动的自相关性越强。图9给出了在微电机个数相同时，不同的振动强度对τ的影响。微电机个数相同时，随着振动强度的增大，τ大体上呈增大的趋势。其中4个微电机作用于手部时，4级和5级的振动强度相较于3级的振动强度τ变小。表明当振幅和频率过大时，也会导致手部运动的相关性下降。

为了更直观的探究微电机个数和不通振动强度对τ的改善情况，定义比值θi

(6)

这里τi表示振动强度为i级时的τ值。计算θi得到了同微电机个数下相关时间随振动强度变化表3。

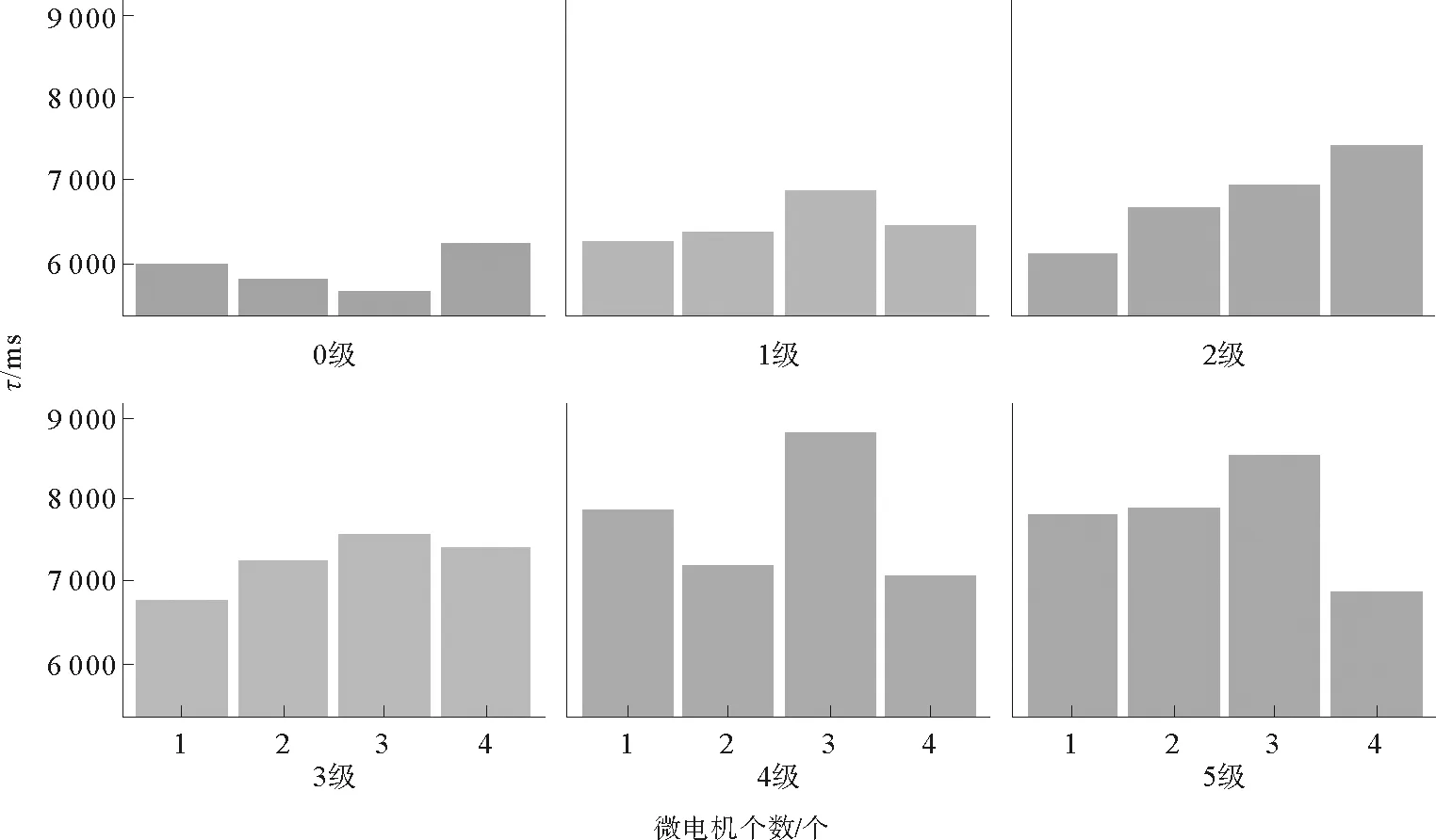
图8 同等振动强度下相关时间随微电机个数变化情况

图9 相同微电机个数下相关时间随振动强度变化情况

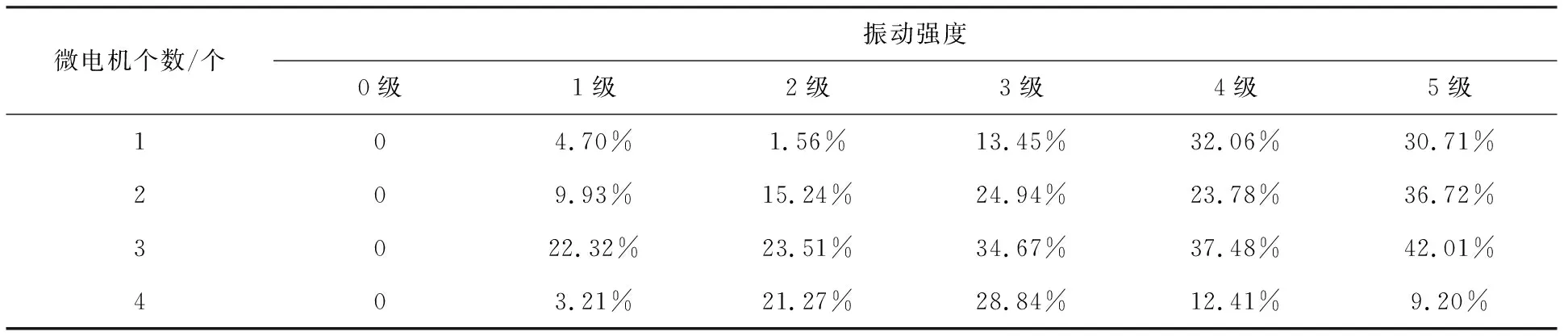
微电机个数/个振动强度0级1级2级3级4级5级104.70%1.56%13.45%32.06%30.71%209.93%15.24%24.94%23.78%36.72%3022.32%23.51%34.67%37.48%42.01%403.21%21.27%28.84%12.41%9.20%

从表3中可以直观地看出微电机个数和不同振动强度对τ的影响。随着振动强度的增加，τ都增大了；微电机个数为3，振动强度为5级时，τ增加了42.01%，激光沿着直线运动时间相关性最好，手部运动的平稳性最好。可以得出振荡共振原理能够提高手部运动长时间的稳定性。

3 结论

本文基于振荡共振原理的基本知识，设计了一套基于振荡共振原理的人体手部运动辅助系统，通过改变微电机个数和振动强度两组因子对人体手部进行的生理实验，研究了振动共振现象对手部运动平稳性的影响。计算不同振幅频率的振动强度作用于手部时的方差值和相关时间值，证实了振荡共振原理可以改善手部运动的平稳性。这些结论为人体医学康复仪器设计和制作提供了很好的生理实验基础。本文只对有限数量微电机和几个明显差异的振动强度进行了实验探究，对于更多数量微电机和更细分的振动强度以及不同年龄段人群的可行性值得进一步研究。

[1]Anderson F C, Pandy M G..Dynamic optimization of human walking[J]. Journal of Biomechanical Engineering, 2001, 123(5):381-390.

[2]Stucki G, Ewert T, Cieza A. Value and application of the ICF in rehabilitation medicine[J]. Disability and Rehabilitation, 2003, 25(11-12):628-634.

[3]Benzi R, Sutera A, Vulpiani A. The mechanism of stochastic resonance[J]. Journal of Physics A General Physics, 1981, 14(11):L453-L457.

[4]Benzi R, Parisi G, Sutera A, et al. Stochastic resonance in climatic change[J]. Tellus, 1982, 34(1):10-16.

[5]Mcnamara B, Wiesenfeld K. Theory of stochastic resonance[J]. Physical Review AGeneral Physics, 1989, 39(9):4854-4869.

[6]Douglass J K, Wilkens L, Pantazelou E, et al. Noise enhancement of information transfer in crayfish mechanoreceptors by stochastic resonance[J]. Nature, 1993, 365(6444):337-340.

[7]Collins J J, Imhoff T T, Grigg P. Noise-enhanced information transmission in rat SA1 cutaneous mechanoreceptors via aperiodic stochastic resonance[J]. Journal of Neurophysiology, 1996, 76(1):642-645.

[8]Fallon J B, Carr R W, Morgan D L. Stochastic resonance in muscle receptors[J]. Journal of Neurophysiology, 2004, 91(6):2429-2436.

[9]Kurita Y, Sueda Y, Ishikawa T, et al. Surgical grasping forceps with enhanced sensorimotor capability via the stochastic resonance effect[J]. IEEE-ASME Transactions on Mechatronics, 2016, 21(6):2624-2634.

[10] Kaut O, Allert N, Coch C, et al. Stochastic resonance therapy in Parkinson's disease[J]. Neurorehabilitation, 2011, 28(4): 353-358.

[11] Hur P, Wan Y H, Na J S. Investigating the role of vibrotactile noise in early response to perturbation[J]. IEEE Transactions on Biomedical Engineering, 2014, 61(6): 1628-1633.

[12] Rogan S, Radlinger L, Hilfiker R, et al. Feasibility and effects of applying stochastic resonance whole-body vibration on untrained elderly: a randomized crossover pilot study[J]. BMC Geriatrics, 2015, 15(1):1-8.

[13] Wang K K, Wang Y J, Li S H. Stability and stochastic resonance for a time-delayed cancer development system subjected to noises and multiplicative periodic signal[J]. Fluctuation and Noise Letters, 2017, 16(3): 1750022.

[14] Wang K K, Xu Z R,Wang Y J , et al. Stochastic resonance for a forest growth system subjected to non-Gaussiannoises and a multiplicative periodic signal[J]. Chinese Journal of Physics, 2017, 55(4): 1387-1399.

[15] Wang K K, Wang Y J, Li S H, et al.Double time-delays induced stochastic dynamical characteristics for a metapopulation system subjected to the associated noises and a multiplicative periodic signal[J]. Chaos, Solitons and Fractals, 2017, 104: 400-417.

[16] Landa P S, McClintock P V E. Vibrational resonance[J]. Journal of Physics A Mathematical and General, 2000, 33(45):L433-L438.

[17] Ren Y H, Duan F B. Theoretical and experimental implementation of vibrational resonance in an array of hard limiters[J]. Physica A Statistical Mechanics and Its Applications, 2016, 456:319-326.

[18] 任昱昊, 季冰, 许丽艳,等. 振荡随机共振的信噪比增益研究与电路仿真[J]. 复杂系统与复杂性科学, 2015, 12(1):104-109.

RenYuhao, Ji Bing, XuLiyan, et al. Research and circuit simulation on SNR gain of vibrational stochastic resonance[J]. Complex Systems and Complexity Science, 2015, 12(1):104-109.

[19] Ullner E, Zaikin A, GarcíA-Ojalvo J, et al. Vibrational resonance and vibrational propagation in excitable systems[J]. Physics Letters A, 2003, 312(5/6):348-354.

[20] STMicroelectronics N V. RM008 Reference manual[DB/OL]. [2012-8-20]. http://www.st.com.

[21] Laganiere R. Opencv 2 Computer Vision Application Programming Cookbook[M]. Birmingham:Packt Publishing, 2011:168-188.

[22] opencv.org. The opencv reference manual release.2.4.13.0[DB/OL]. [2016-5-12]. http://docs.opencv.org.

[23] 盛骤. 概率论与数理统计[M]. 第3版.北京:高等教育出版社, 2008:100-110.

[24] 吴祈耀, 朱华, 黄辉宁. 统计无线电技术[M]. 北京:国防工业出版社, 1980:75-90.