“海上丝绸之路”集装箱航运网络路由策略研究

封学军，张 铖，蒋柳鹏，张 艳，蒋 鹤

(河海大学港口海岸与近海工程学院，南京 210098)

0 前言

“海上丝绸之路”作为中国“一带一路”战略的重要组成部分，其核心是港口和航线构成的航运网络，成为中国与沿线国家沟通的重要通道。“海上丝绸之路”航运网络主要由港口、航线、船舶等要素构成，其属于典型的复杂网络[1]。近年来，随着小世界网络和无标度网络的提出，复杂网络理论成为目前针对复杂系统进行研究的热点工具之一。复杂网络理论将真实系统的各个要素及要素之间的关系转化为网络中的节点和节点间的边，以网络的形式描述系统中的各部分的关系，强调系统的拓扑性质，揭示现有系统的本质和演变机理[2-3]。

复杂网络已经成功应用于互联网、交通运输系统、社会经济等多个领域，取得了大量的研究成果[4-6]。近年来，复杂网络理论也被应用于港口航运系统的研究，为港口航运系统的动力学问题提供了全新的研究工具，复杂网络视角下，集装箱航运网络的研究是当前港口航运系统研究的前沿问题之一[7]。当前其主要成果集中在两个方面：首先是港口航运网络复杂性分析，田炜对Maersk Line航运网络进行分析，得出其网络具有局部节点最短距离过大，大部分节点具有较大的集聚系数等特性[8]；牟向伟以CMA-CGM公司班轮网络数据进行分析，发现集装箱班轮网络具有较短的平均距离和较大的集聚系数[9]；武配剑、胡一紘、吕康娟等学者分布以集装箱航运网络、世界海运网络、干散货网络和世界航运城市网络为对象，均得出其网络具有无标度性和小世界性[10-12]；其次是航运网络管理及优化问题，熊文海、颜章龙分析了世界航运网络的结构特性和动力学机制，指出世界航运网络的演化趋势[13-14]；宗康、Jiang等学者基于复杂系统理论，研究了航运网络的连通性问题，指出航运网络的连通性主要由一些枢纽港口的稳定性决定，应优先保证枢纽港口的正常运营[15-16]；张其林、文宏等分析了在无标度网络的性能提升策略和优化方法，指出无标度网络优化的主要参数和内容[17-18]。

综上所述，当前研究成果主要集中在航运网络的复杂性和演化趋势分析上，缺乏针对航运网络的拓扑性质和路由策略方面的研究成果。因此，本文依托复杂网络理论，对“海上丝绸之路”集装箱航运网络的拓扑性质和路由策略开展研究，该研究具有重要意义。

1 “海上丝绸之路”集装箱航运网络的构建

集装箱航运网络作为交通运输网络的重要组成部分，港口、航线、船舶是港口航运网络的基本构成要素。港口作为航运网络的节点，港口间的航线作为航运网络的边，则可定义“海上丝绸之路”集装箱航运网络为：G(V,E)。其中，V={vi|i=1,2,…,n}为网络的节点，即海上丝绸之路沿线港口，n为港口的数量，n=706，E={eij|i,j=1,2,…,n,i≠j}表示网络的边，即海上丝绸之路港口间的航线。由于集装箱航线大多循环布置，因此不考虑边的方向，即为无向无权的网络模型。

本文数据来源于中国国际海运网(http://ship.shippingchina.com/)的集装箱班轮船期数据，时间范围为：2016年7月1日-2016年11月1日，节点范围为：在海上丝绸之路沿线国家的港口。边的范围：中国国际海运网中海上丝绸之路沿线国家港口间所有班轮航线，并剔除重复的航线。该航运网络中港口节点为706个，边有8754条。其邻接类型选择为L型，即当航线由港口v1经过港口v2达到港口v3时，认为v1和v2是相连的，v1和v3不连接。以邻接矩阵作为网络的存储方式，运用R语言中“igraph”程序包对航运网络进行可视化处理，航运网络示意图如图1所示。

2 “海上丝绸之路”集装箱航运网络类型的拓扑性质分析

2.1 常用复杂网络特性及其主要特征

随着网络理论的突破性发展，网络分析的评价方法体系不断充实和完善，为“海上丝绸之路”航运网络的评价提供了更为科学的分析手段，目前主流的复杂网络特性及其特征如表1所示。

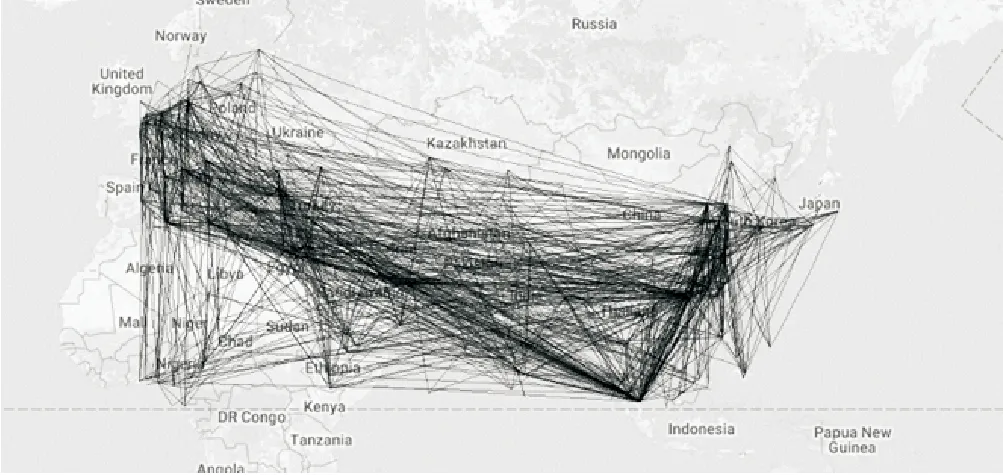
图1 “海上丝绸之路”航线网络连接示意图Fig.1 Illustration diagram of the “Silk Road on the Sea” route network

序号复杂网络特性特征条件1规则网络度分布p(k)符合δ函数2小世界特性平均距离小,集聚系数高3无标度特性度分布p(k)符合幂律分布4随机特性度分布p(k)为泊松分布

由表1可以发现，通过分析网络的主要特征，例如度分布、平均距离、集聚系数就可以判断该网络的主要特性，故本文构建集装箱港口航运网络的指标集合：

S={P(k),L,CI}

(1)

式(1)中，S为集装箱港口航运网络的指标集，P(k)为网络的度分布，L为网络平均距离，CI为网络平均集聚系数。通过网络的指标集合S可以判断出“海上丝绸之路”集装箱航运网络的主要特性。

2.2 集装箱航运网络特征集的计算方法

网络的度分布P(k)：在集装箱港口航运网络G中，港口vi的度ki指与港口vi直接相连的边数，反映网络节点的联通程度这一局部特征。通过计算网络G中节点的度值ki，可以计算出网络中所有节点的度值ki的分布情况P(k)。

平均距离L：平均距离L是网络中两个港口之间相互连接需要经过的最少边数。对所有港口对之间的距离求平均值即可得集装箱航运网络的平均距离。其计算公式如下：

(2)

式(2)中，L为网络的平均距离，dij为网络节点vi和vj之间的距离，即港口vi和港口vj连接需要最少的边数，N为网络总节点数。

集聚系数CI表示与网络中某个节点相连的各个节点之间也相互连通的可能性。某个港口vi的集聚系数等于与该港口相连的所有节点之间(除去该港口)相连的边的数目占可能存在的最大边数的比例。计算公式如下：

(3)

式(3)中，CI为网络的平均集聚系数，ki为港口vi的度，ki(ki-1)/2为ki个港口之间两两相连可以存在的最大边数，Mi为航线网络中ki个港口节点之间存在的边数，N为网络总节点数。

2.3 “海上丝绸之路”航运网络的网络类型和拓扑性质

对“海上丝绸之路”集装箱航运网络所有节点进行度分布统计分析可得该网络的度分布P(k)，如图2所示，在该网络中，港口的度分布极不平均，即度很大的港口较少，集中在几个港口，度较小的港口很多，80%港口的度值均在25以下，对图2中坐标轴取双对数得到图3，拟合结果显示：网络度分布P(k)符合指数为-3的幂指数分布(p-value<0.05)。图像结果表明，“海上丝绸之路”航线网络分布符合幂指数分布，曲线拟合较好。

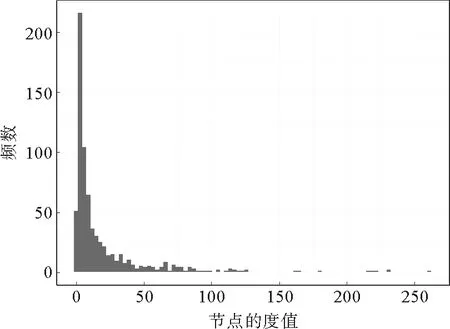
图2 “海上丝绸之路”航运网络度值分布图Fig.2 Distribution of degree of the “Maritime Silk Road” shipping network

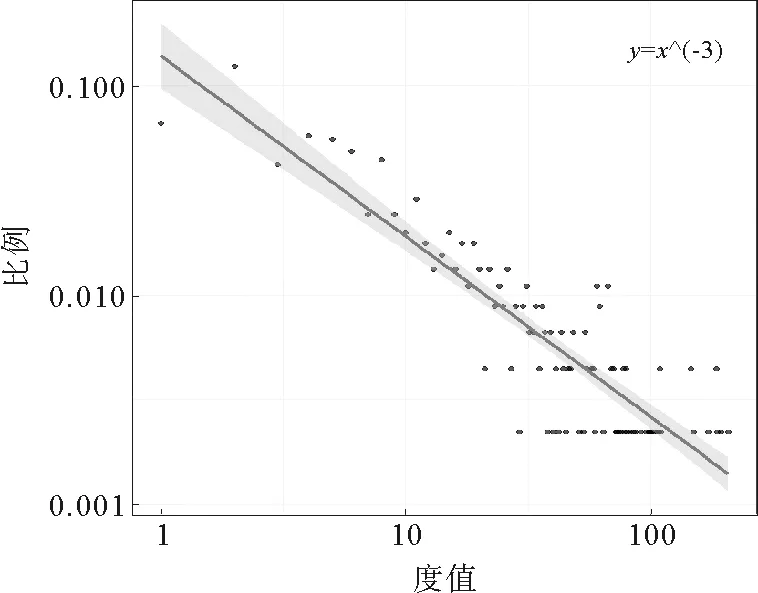
图3 双对数坐标轴下各度值节点数占总体的比例图Fig.3 Proportion of different degree vertex in double logarithmic axis

通过计算可得，“海上丝绸之路”航运网络平均距离L=2.799，即在网络中任意两个港口间平均只需经过3个中间港口即可完成运输。所有节点距离均小于6；网络集聚系数平均值CI=0.574，在该网络中，80%以上的港口节点的聚集系数分布在[0.3,0.9]之间。

结果表明：“海上丝绸之路”航运网络具有较短的平均距离L和较高的平均集聚系数CI，可判定具有小世界特性；网络度分布P(k)满足幂指数分布规律，而具有无标度特性；网络度分布P(k)符合指数为-3的幂指数分布(p-value<0.05)，因此可认为“海上丝绸之路”集装箱航运网络是具有小世界性的BA复杂网络。说明网络中存在着少量的枢纽港口，与这些枢纽直接相连的港口数量非常的巨大，而其他大部分港口只与少量港口直接相连。

3 “海上丝绸之路”航运网络仿真优化模型

基于BA无标度网络性能提升理论，BA无标度网络性能的优化主要针对以下三方面展开：网络拓扑结构，路由算法，网络中节点处理能力，对应于“海上丝绸之路”集装箱航运网络中的航线网络拓扑结构、路由算法、港口处理能力。本文对“海上丝绸之路”集装箱航运网络进行仿真实验，尝试找出相应的性能提升策略。

3.1 模型界定

本文构建“海上丝绸之路”集装箱航运网络仿真模型：以上述网络G(V,E)为基础，添加集装箱作为港口间流动的货物，每个港口具有处理能力C和等待处理队列Q，每个港口在单个时间周期t内可完成C个集装箱的转运，未完成装运的集装箱将被存入等待处理队列。

①在该网络中，集装箱生成量为G(TEU)，通过随机抽样(有放回)选择G组港口作为始发港和目的港，并将所生成的集装箱放入始发港等待处理队列的尾部；

②每个始发港口检查自身等待处理队列最前的集装箱的目的港是否为当前港口，如果为当前港口，则完成运输并将集装箱从网络中删除；否则港口将按照一定的路由规则将集装箱传递到相邻节点。

本文通过控制路由算法参数α来实现对不同路由策略的模拟，路由算法具体如下：如果相邻港口中存在目的节点，该港口会将集装箱转发给目的港口，如果相邻港口中没有目的节点，该港口将按公式(4)转发给其邻居节点之一。

(4)

式(4)中，Pi为该港口将集装箱发送给其邻居港口vi的概率，ki为该港口的邻居港口vi的度，α为路由算法参数，不同的α值代表不同的集装箱路由策略。α值越大，表明网络中集装箱越倾向于通过枢纽港口进行中转，现实航运网络中，港口的寡头趋势越来越明显，枢纽港口在航运网络中的作用越来越明显。

为描述航运网络的整体通畅程度，我们定义集装箱港口航运网络的拥塞度η为：

(5)

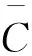
3.2 “海上丝绸之路”航运网络性能优化实验

论文针对不同的网络路由算法、节点处理能力配置方案进行理论分析，以提出合适的港口航运网络性能提升策略。根据BA无标度网络理论和港口航运网络的结构特征[18]，可得到如下2个定理：

定理1对于BA复杂网络应用公式(4)所示的路由算法，网络的拓扑结构决定了节点i获得相邻节点转发的货物数正比于该节点度值ki的1+α次方。

目前，我还在负责阿里的国际化、生态体系建设、文化建设以及经济体协同等方面的工作，在接下来的一年里，我也会做好交接。

定理2在网络随机产生货物时，所产生的货物的运输目的地节点是节点i(度值为ki)的相邻节点的概率正比于节点i的度ki。

基于以上两个定理，设计仿真实验，通过不同实验结果的对比选择最优的网络性能提升策略。

4 网络性能优化策略仿真实验

仿真实验程序基于Java平台，对集装箱在“21世纪海上丝绸之路”集装箱航运网络中生成、运输、发送和移除的过程进行模拟。通过调整节点处理能力C、路由算法参数α两个核心参数，分析不同参数组合下网络中集装箱生成速率G对网络拥塞度η的影响，实现对网络不同状态的模拟。实验将分为两阶段共六组对照实验，第一阶段实验模拟网络在节点处理能力C为给定的情况下，不同路由算法参数α对网络的影响，第一阶段实验方案见表2。

表2 第一阶段实验方案设计表Tab.2 The program table of the first stage experimental

第1组实验：分析当节点处理能力C均为常数时，不同路由算法参数α对网络拥塞度η影响，其结果如图4所示。

由图4可知：当α=0，及集装箱选择节点与节点度无关时，网络的拥塞值η最小，故当C均为常数下，α=0为最佳路由算法参数。

第2组实验：分析在提高处于枢纽港口(在度分布中度值ki处于前3%的港口)的处理能力C1对整个网络性能的影响，本文取C1=30，非枢纽港C2=20，其实验结果如图5所示。

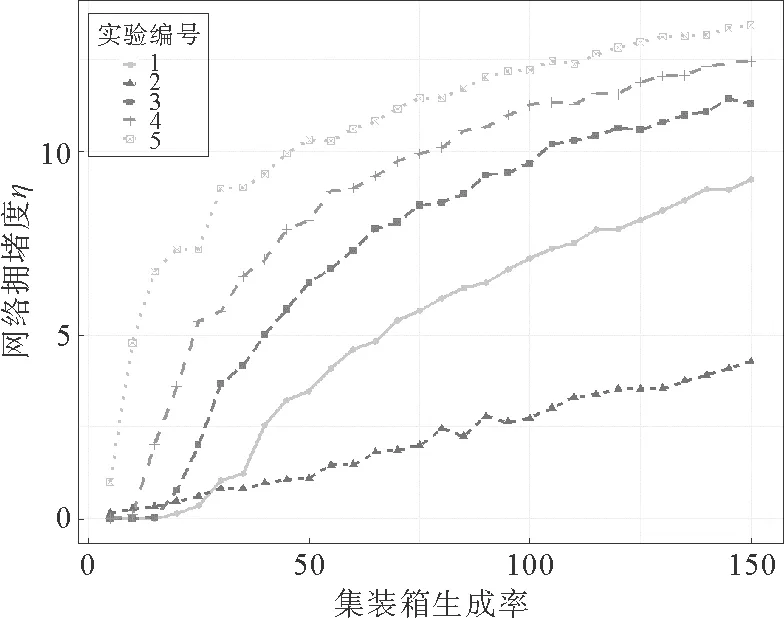
图4 C均为常数，不同α下“海上丝绸之路”航运网络拥塞度的影响Fig.4 Capability of the “Maritime Silk Road” shipping network in different α value and C value in the same conditions

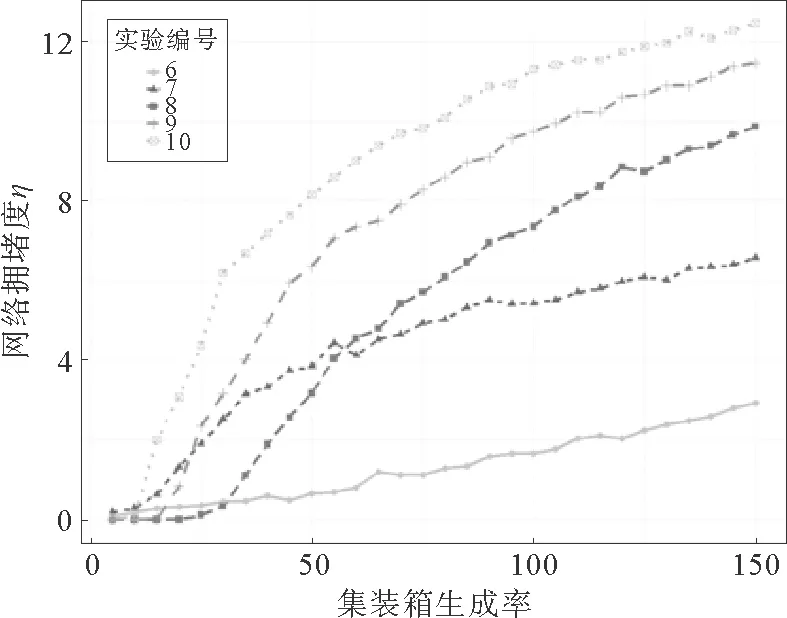
图5 提高枢纽港容量下α值对“海上丝绸之路”网络拥塞度的影响Fig.5 Congestion of the “Maritime Silk Road” shipping network when improve the α value of hub port

由图5可知，当提高系统中处于枢纽港口的处理能力，α=-1时网络拥塞值η最小，即α=-1为最佳路由算法参数。这一结果也证明了定理1的正确性，即当α=-1时，节点i获得相邻节点转发的货物数正比于该节点度值ki，集装箱将分散到网络中各个港口而非集中于枢纽港口，整个网络荷载较为合理。

第3组实验：为了对网络中港口的处理能力配置进行分析，以实现在网络总处理能力约束下降低网络的拥塞值。根据定理1，节点得到货物的概率正比于ki的1+α次方，因此第3组实验设置Ci=βki，β为总处理能力约束参数，保证港口节点的总处理能力基本不变，本文取β=1，其结果如图6所示：

由图6可知：当Ci=βki时，即α=1时，网络的拥塞值η最低，即α=1为最佳路由算法参数。即实现了在整体港口处理能力约束下，网络的拥塞值最小。

第1阶段实验模拟网络在节点处理能力C为给定的情况下，不同路由算法算法参数α对网络的影响，第2阶段实验模拟网络在已知最佳路由算法参数α的情况下，不同情景下C配置变化对网络拥塞值η的影响。第2阶段实验方案如表3所示。

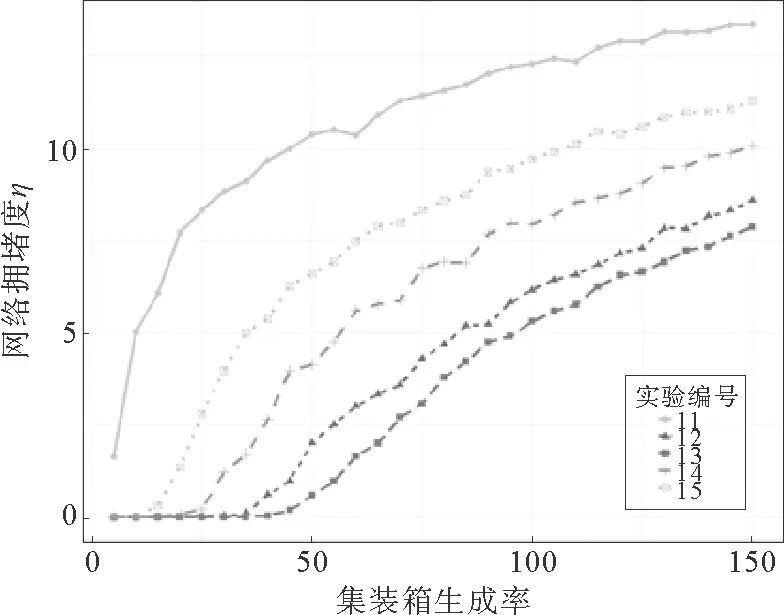
图6 在Ci=βki时，α值对“海上丝绸之路”航运网络拥塞度的影响Fig.6 The influence of α on Congestion of “Maritime Silk Road” shipping network when Ci=βki

实验组别实验编号实验参数港口总体处理能力四16α=0,C=107,06017α=0,C=2014,12018α=0,C=3021,180五19α=-1,C1=20,C2=107,48020α=-1,C1=30,C2=1510,90521α=-1,C1=40,C2=2021,390六22α=1,Ci=βki,β=113,34923α=1,Ci=βki,β=226,69824α=1,Ci=βki,β=340,047

第四组实验：由第1组实验可知，当网络中所有节点处理能力均为C时，最佳路由算法参数α=0，第4组实验分析当α=0，网络中所有节点处理能力均为10，20和30时，网络的拥塞度η随着集装箱生成速率G的变化情况，其结果如图7所示。

由图7可知，当α=0，随着节点的处理能力C增大，“海上丝绸之路”航运网络的拥塞度η逐渐降低，且效果与C的提升幅度成正比。符合海上丝绸之路集装箱航运网络中增加港口作业能力，降低港口拥塞的现实情况。

第5组实验：第2组实验中当网络中核心港口(度排名前3%)通过能力C1和非核心港口通过能力C2不一样时(C1>C2)，α=1为最佳路由算法参数。第5组实验分析当C1和C1同时增大时，网络的拥塞度η随着集装箱生成速率G的变化情况，其结果如图8所示。

图7 C为常数且α=0时，不同的平均处理能力对“海上丝绸之路”航运网络拥塞度的影响Fig.7 When C is a constant and α=0, effects of different average processing capabilities on congestion of “Maritime Silk Road” shipping network

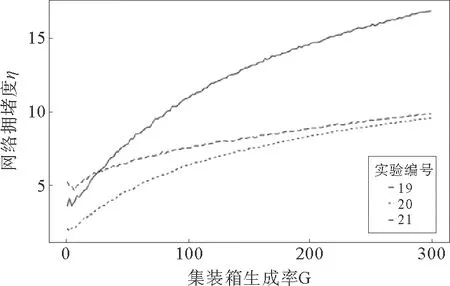
图8 C1≠C2且α=-1时，C1和C2变化对“海上丝绸之路”航运网络拥塞度的影响Fig.8 When C1≠C2 and α=-1, the effects of different capabilities on congestion of “Maritime Silk Road” shipping network

图9 Ci=βki且α=1时，β值变化对“海上丝绸之路”航运网络拥塞度的影响Fig.9 When Ci=βki and α=1, the effects of different β on congestion of “Maritime Silk Road” shipping network

由图8可知，当α=-1时，随着C1和C2的同时提升，第20号实验(C1=30，C2=15)和21号实验(C1=40，C2=20)的拥塞度η比第19号实验效果有所提升，但是21号实验相对20号实验的提升效果不如20号实验相对19号实验的提升效果提升明显，存在规模递减效应。

第6组实验：第3组实验中当Ci=βki时，即α=1时，网络的拥塞值η最低，即α=1为最佳路由算法参数。第6组实验分析当α=1，β值变化时，网络的拥塞度η随着集装箱生成速率G的变化情况，其结果如图9所示。

由图9可以看出，当网络中节点的通过能力Ci=βki，α=1时，随着β值的提升，网络拥堵的出现时间发生了后移，网络的拥塞有所改善。增加β值，可有效改善“21世纪海上丝绸之路”集装箱航运网络的拥塞情况。

5 结论

本文以“海上丝绸之路”集装箱航运网络为研究对象，通过构建网络特征集并对网络指标进行计算，得出其网络同时具有小世界性和无标度性，并对其网络的度分布进行数值拟合，其幂律分布的幂的阶次为-3，得出“海上丝绸之路”航运网络属于BA复杂网络的结论。

基于BA网络的性能优化理论，本文构造网络拥塞度η，设计两阶段共六组24个仿真实验，第一阶段实验分析在Ci给定时，分析Ci为常数、C1>C2、Ci=βki三种情况下，路由算法参数α变化时，网络的拥塞度η随着集装箱生成速率G的变化情况，并找出每种Ci配置对应的最佳α值。第1阶段3组实验表明：当网络中Ci均为同一常数时，α=0为最佳路由算法参数；当C1>C2时，α=-1为最佳路由算法参数；当Ci=βki时，α=-1为最佳路由算法参数。第二阶段实验在已知α值，通过变化三种情况下Ci的数值，分析Ci数值大小对网络的拥塞度η的影响。第2阶段三组实验表明：当Ci均为同一常数时候，提升常数值，网络的拥塞度η降低，且效果与Ci的提升幅度成正比；当C1>C2时，同时提升C1与C2的大小，网络的拥塞度η降低，但降低效果与Ci的提升幅度相比逐渐降低，存在规模递减的情况；当Ci=βki时，提升β值，网络的拥塞度η降低，且效果与Ci的提升幅度成正比。

本文研究了“海上丝绸之路”集装箱航运网络的网络拓扑特性，并对该网络的核心参数做了计算机仿真实验，讨论了不同参数组合对网络拥塞度的影响。但是目前学者对该网络的动力学过程、特别是集装箱流传播的认识仍有不完善之处，这也是本文下一步研究的方向。

[1]Wang N, Wu N, Dong L L, et al. A study of the temporal robustness of the growing global container shipping network[J]. Scientific Reports, 2016, 6, 1-10.

[2]Watts D j, Strogatz S H. Collective dynamics of “small-world” networks[J]. Nature, 1998, 393(6684), 440-442.

[3]Barabasi A L, Albert R. Emergence of scaling in random networks[J]. Science, 1999, 286(5439): 509-512.

[4]Albert R, Jeong H, Barabasi A L. Internet-diameter of the World-Wide Web[J]. Nature, 1999, 401, 130-131.

[5]Summers, T. China's 'New Silk Roads': sub-national regions and networks of global political economy[J]. Third World Quarterly, 2016, 37(9):1628-1643.

[6]Buldyrev S V, Parshani R, Paul G, et al. Catastrophic cascade of failures in interdependent networks[J]. Nature, 2010, 464, 1025-1028.

[7]Bartholdi J J, Jarumaneeroj P, Ramudhin A. A new connectivity index for container ports[J]. Maritime Economics & Logistics, 2016, 18(3):231-249.

[8]田炜，邓贵仕，武佩剑. 世界航运网络复杂性分析[J]. 大连理工大学学报，2007, 47(4), 605-609.

Tian Wei, Deng Guishi, Wu Peijian. Analysis of complexity in global shipping network[J]. Journal of Dalian University of Technology, 2007, 47(4), 605-609.

[9]牟向伟，陈燕，杨明. 班轮航运网络拓扑特性[J]. 大连海事大学学报，2009, 35(2), 34-37.

Mou Xiangwei, Chen Yan, Yang Ming. Topological features of liner shipping network[J]. Journal of Dalian Maritime University, 2009, 35(2), 34-37.

[10] 武佩剑，邓贵仕，田炜. 集装箱航运网络拓扑特性研究[J]. 武汉理大学学报(交通科学与工程版)，2008, 32(4), 665-668.

Wu Peijian, Deng Guishi, Tian Wei. Topological features of liner shipping network[J]. Journal of Wuhan University of Technology(Transportation Science & Engineering), 2008, 32(4), 665-668.

[11] 胡一竑. 基于复杂网络的交通网络复杂性研究[D]. 复旦大学，2008.

Hu Yihong. Research on traffic network complexity based on complex network[D]. Fudan University, 2008.

[12] 吕康娟，张蓉蓉. 基于复杂网络的世界航运中心网络结构与特征[J]. 系统管理学报，2012, 21(1), 86-92.

Lv Kangjuan, Zhang Rongrong. On the structure and characteristics of international shipping center based on complex network theory[J]. Journal of Systems Management, 2012, 21(1), 86-92.

[13] 熊文海．世界航运网络的结构特性及其动力学行为研究[D]．青岛大学，2009．

Xiong Wenhai. Structural characteristics and dynamic behavior of the world shipping network[D]. Qingdao University, 2009.

[14] 颜章龙．世界海运网络拓扑结构及演化规律研究[D]．大连海事大学，2013．

Yan Zhanglong. Research on evolution motion of world shipping complex network[D]. Dalian Maritime University, 2013.

[15] 宗康，胡志华．基于复杂网络的海运航线网络连通性分析[J]．大连海事大学学报，43(1)，80-84，2017

Zong Kang, Hu Zhihua. Research on the connectivity of shipping route network based on complex network[J]. Journal of Dalian Maritime University, 43(1), 80-84, 2017.

[16] Jiang J L, Lee L H, Chew E P． Port connectivity study: an analysis framework from a global container liner shipping network perspective[J]． Transportation Research Part E: Logistics and Transportation Review, 2015, 73, 47-64．

[17] 张其林，董政呈，赵永标. 一种具有核心—边缘结构的无标度网络演化模型[J]. 计算机工程与科学，2017，39(3)，500-504.

Zhang Qilin, Dong Zhengcheng, Zhao Yongbiao. A scale-free network evolving model with core-periphery structure[J]. Computer Engineering and Science, 2017, 39(3), 500-504.

[18] 文宏，樊晓平，张会福，等. BA无标度网络性能优化方法研究[J]. 小型微型计算机系统，2016，37(8)：1812-1815.

Wen Hong, Fan Xiaoping, Zhang Huifu, et al. Research on BA scale-free networks performance optimization[J]. Journal of Chinese Computer Systems, 2016, 37(8): 1812-1815.