数学课堂教学中问题情境的创设艺术

广东徐闻县第一中学 方良京

教育家第斯多惠说：“教学的艺术不在于传授的本领，而在于激励、唤醒、鼓舞。”创设适宜的问题情境，正是关于激励、唤醒、鼓舞的一种教学艺术。好的情景教学不仅能够提高学生的学习兴趣，提高教学效率，而且有利于培养师生之间的情感交流，为学生创造一个良好的学习氛围。那么在数学课堂教学中如何创设问题情境呢？

一、趣例激疑，营造和谐氛围

兴趣是激发学生主动学习的催化剂，在课堂上教师要依照知识的科学性和趣味性，选用适当的趣例来设置疑问，诱发学生急于解疑的心态，激起学生强烈的学习动力。

例如，在“等比数列求和”的教学中，我先讲述一个故事：从前有人卖了一匹马得钱1560元，但买主反悔，认为这匹马根本不值这么多的钱，要把马退给卖主。可卖主提出新的条件：“既然你嫌贵，如果你能改买马蹄子上的钉子，我就把马白送你如何？”买主听后略加思索便问卖主怎个卖法。卖主讲，每个马蹄子上有6枚钉子，共24枚，

二、引入矛盾，于无疑处生疑

古人云：“于无疑处有疑，方为进矣”。在课堂教学中往往出现书上怎么说，学生就怎么回答的情况，“书”云亦云，如何医治这种毛病？有效手段就是教师要适时引入矛盾，于无疑处生疑，活跃学生思维，树立创新意识。

例如，在“双曲线概念”的教学过程中，学生在已有椭圆概念的基础上，通过预习，对课本所述双曲线定义：“平面内与两个定点F1、F2 距离的差的绝对值是常数（小于F1F2）的点轨迹叫做双曲线。”似乎没有什么疑问了，其实这种无疑往往不是真正无疑，而是没有用心体会定义，没有深入思考的表现，这时在教学过程中可以设问：

（1）定义中“平面内”三字可以去掉吗？

（2）如果把定义中“绝对值”三字去掉，其轨迹又是怎样呢？

（3）定义括号内的条件“小于F1F2”改为“等于F1F2”，这时点的轨迹又是什么呢？

在这里，于学生“无疑”处生疑，让学生经历了“无疑——有疑——无疑”的过程，使学生对此概念的内涵和外延理解得更加深入和透彻。

三、课堂开头，巧妙设置悬念

悬念是指学生对新学知识感到不解而产生的迫切等待的心理状态。因此，教学中教师要根据教学的需要，精心设计悬念，“吊”足学生的胃口，激发学生探究知识的欲望，使学生集中注意力，丰富了想象。

例如，在教学“等差数列的通项公式”时，我们是用不完全归纳法得到的。但这种方法很不严密，有时得出荒谬的结论。比如，一个数列的通项公式是，当n=1、2、3、4时，我们能说对于任意吗？不能！那么要证明公式。对仅仅n∈N*都成立。因为自然数的个数有无穷多个，无论如何也试不完，用完全归纳法是行不通的。对于这类问题，有没有一种既可靠严谨，又易于操作的方法呢？有！这就是我们这节课要讲的《数学归纳法》。这就诱发了学生心理上的悬念，使学生有一种追根求源之感，求知的热情自然而生，因此对接下来课堂的内容也会更容易接受。

四、疑感错误，善于设置陷阱

教学中，针对学生对某些数学概念、法则、定理、公式等方面理解肤浅而表现在判断、推理及解题上的失误现象，有的放矢地选编一些颇具迷惑性的题目，在易错的节骨眼上布设“陷阱”，“诱”使学生误入歧途，引发争论，辨析正误，使学生增长防御陷阱的经验，取得学习的主动权。

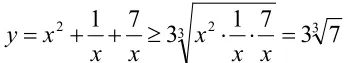
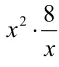
通过上述引导，不仅使学生从“陷阱”中跳出来，更主要的是能使学生逐步养成用批判的态度来对待每一个问题的习惯，从而培养了学生思维的批判性。

总之，作为数学教师应当把创设最佳的问题情境作为自觉设计教学过程的产物，并惯穿于教学过程的始终，以获取最大的教学效益。换句话说，创设数学教学问题情境，已成为课堂教学改革的切入点。

创设问题情境可以更好地抓住青少年学生的好奇心理，引起学生主动学习的兴趣，以达到事半功倍。