浅谈充分必要条件解题技巧

广东英德市英德中学 邓金华

一、充分必要条件常见的题型分析

充分必要条件常见的题型是选择填空题，但是不管是选修2-1新授课时，还是高三即将参加高考的考生，会有相当一部分同学遇到关于充分必要条件试题时，无法正确作答，下面针对此类题型介绍处理的思想方法，能有效的帮助学生掌握解题的思想和方法首先，要明确充分必要条件题目的本质都可以归结为是两个对象元素的范围问题，不同的只是背景不同，可以是圆锥曲线，不等式，集合等等；其次，充分必要条件是满足一个原则“小范围推出大范围，大范围推不出小范围”，并且推出符号“⇒”左边是充分条件，右边是必要条件，最后，要解决此类题的关键是结合语文知识中语句的抽取主干（主谓宾）思想。下面我们通过例子分析问题：

二、典例剖析

（一）判定充分必要条件关系

例1.是方程表示椭圆的（ ）

A 充要条件 B 充分不必要条件

C 必要不充分条件 D 既不充分也不必要条件

解：

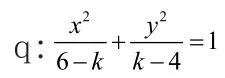
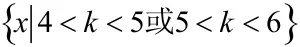
所以，即是表示椭圆的必要不充分条件，故选C

小结：本题的难点是在发现“p的范围大，q的范围小”的时候怎么确定p,q的充分必要关系，在题目中给出了p,q两个条件，需要先求出两个条件代表的范围，根据“小范围推出大范围，大范围推不出小范围”原则写出p,q的符号关系“”，再从符号关系读出p是q的必要不条件, 从符号关系pq≠＞可以读出p是q的不充分条件系，所以p是q的必要不充分条件。

（二）利用充分必要条件关系求参数范围

例2. 已知，，若¬p 是 ¬q 的必要不充分条件，则实数a的取值范围是（ ）

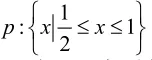
∴pq¬¬是的必要不充分条件，∴q是p的必要不充分条件，

∴p是q的充分不必要条件，

小结：本题的难点是分析出题目中p，q代表的范围大小关系，题目提供了两个条件其中一个带有参数，首先求出两个条件代表的范围，利用逆否命题的等价性把的必要不充分条件转化为q是p的必要不充分条件，接着利用“主谓宾”分析p,q关系，“q是p的必要不充分条件”提取“主谓宾”可以得到“q是必要条件”“q是不充分条件”，其中“q是必要条件”转化为符号是“⇒q”, “q是不充分条件”转化为符号是“p≠＞”,最后把得到的两个符号补充完整得到p,q关系是“ q ⇒ p , p ≠＞q ”，所以得到的结论q是代表的范围小，p的范围大，利用数轴就可以得到不等式组。

（三）证明充分必要条件关系

例3.证明：ABC∆是等边三角形的冲要条件是

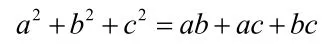
这里a,b,c是ABC∆的三边。

证明：（1）充分性：如果，那么

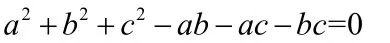
所以

所以

即 a=b=c

所以是ABC∆等边三角形。

（2）必要性：如果ABC∆是等边三角形，那么

所以

所以

所以。

小结：关于充要条件的证明，需要分为证明充分性和必要性两个步骤，学生容易在答题中把证明的两个步骤证明反了，因此分析清楚充分性必要性证明方向异常重要；首先，分析题目中哪个是条件，哪个是结论，利用“主谓宾”思想，，其次，要明确充分性是从条件证向结论，必要性是结论证向条件；从题目中可以提取出“主谓宾”的表达是“条件是”，因此，充分性证明：已知条件是“”，需要证明的结论是“∆ABC是等边三角形”；必要性证明，已知条件是“∆ABC是等边三角形”，需要证明的结论是“”。

从以上的例子可以发现充分必要条件的解题关键是分析出关于p,q的范围，并且掌握从充分必要条件的符号翻译成文字描述，也能够从文字描述的关系转化为符号表达，就能理清楚题目的意思，进而求解。