极坐标的简单应用

广西柳州地区民族高级中学 王文刚

极坐标是新课标选考内容之一，由于是新增的内容，考纲要求比较简单，只有理科学生学，所以在高考中一般以基础题目出现，而圆锥曲线是高考的热点，常以压轴题的形式出现。圆锥曲线问题的基本解题思路，就是借助点的坐标来表达条件，但是，在很多具体问题中，很多几何条件并不方便借助点的直角坐标来表达，从而导至运算繁琐，运算量过大，使得学生望而生畏，半途而废。随着对极坐标知识的深入学习，利用极坐标知识解决某些圆锥曲线问题，常可以化繁为简，高效解答。特别在圆锥曲线的焦点弦类问题及题设中含有垂直、特殊三角形等等这类问题时带来方便。下面举例说明。

一、题设中含有垂直关系

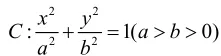
（1）求椭圆C的标准方程；

（2）,,D M N为椭圆C上的三个动点，D在第一象限，M, N 关于原点对称，且

求∆DMN的面积最小值时， 点的坐标.

（2）方法一：（常规解法）由题意知ODMN⊥，设，

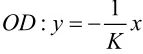
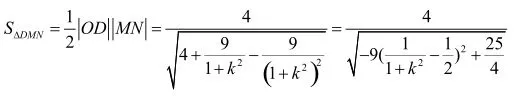
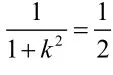
方法二：（极坐标法）如图：以直角坐标系中的原点O为极点，x轴非负半轴为极轴建立极坐标系.设D(ρ1, θ)

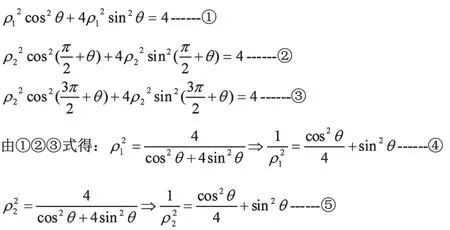
评注：比较以上两个方法我们可以看到，合理建立极坐标系，利用极坐标系建立相关关系，可以避免繁琐的运算而使问题得到快速解决，彰显极坐标法的好处。

二、圆锥曲线焦点弦问题

1.圆锥曲线的统一极坐标方程的推导及结论

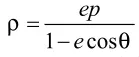
2.圆锥曲线的焦点弦问题是高考考查的重点，热点，圆锥曲线的极坐标方程解决这类问题带来了简便方法，有效地避免繁琐的代数运算。

（1）求椭圆C的标准方程；

（2）若抛物线上存在两个点M,N，椭圆上也存在两个点P,Q,使M, N, F2三点共线，

P, Q, F2三点共线，且PQ⊥MN，求四边形PNQM面积的最小值.

（2）如图以椭圆的右焦点 F2为极点， F2x为极轴建立极坐标系，

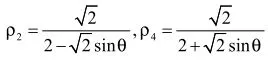
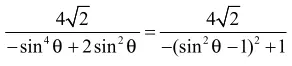
评注：本题若用常规方法求解，要经过繁琐的代数运算，给解答带来不便，而利用极坐标方法，合理选择相应的方程解决问题，可起到事半功倍的作用。以上角度只是对极坐标在求解圆锥曲线某些类问题的一个初探，事实上，在高考中考查类似的问题有很多，这里就不一一列举了，这里起到一个抛砖引玉的作用。