如何让学生能做大一些的事情——再学“新课标下的小学数学教学设计”讲座有感

河北孟村县育才小学（061400）

河北东光县找王镇后屯小学（061600） 孙国元

最近，我再次在河北省中小学教师全员远程培训平台上观看了北京教科院范存丽老师的讲座“新课标下的小学数学教学设计”。讲座深入浅出、精彩至极，尤其是“让学生能够独立地做大一点的事情”的观点，更是对数学课程标准修订版的最好诠释。基于“让学生能做大一些的事情”理念，范老师评点了“圆的周长”的一个教学案例。我对其评点持有异议，现写出来与同仁商榷。

［教学案例］“圆的周长”第二次试教的基本环节。

1.结合如图1的直观图，猜想圆的周长与什么有关。

图1

图2

2.结合图2所示的直观图，进一步猜想圆的周长与直径有怎样的关系。

3.学生提出验证猜想的方法后，用手中的学具测量，想清量什么，量完后怎么办，并完成下表的表头设计。

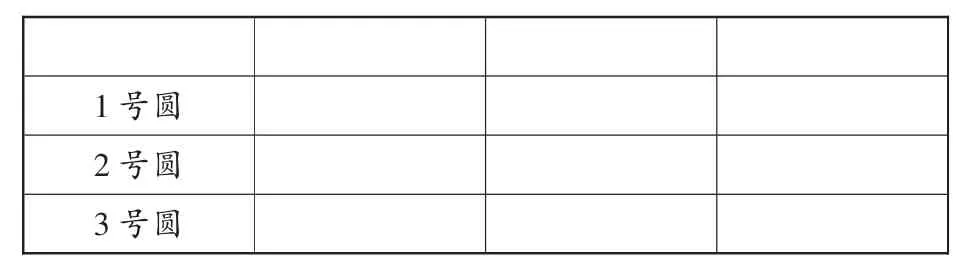
1号圆2号圆3号圆

4.操作并填表。学生用计算器计算周长与直径的倍数关系，记录在表中。

5.汇报。得出公式C=dπ后，进一步了解相关的数学文化。

6.练习。

异议一：环节1对启发学生思维颇有好处，但直接给出这组同心圆，简化了思考和探究的过程，缩小了思维活动空间，不利于学生积累活动经验和发展创新思维。

异议二：环节2中所创设的正方形、圆、正六边形的组合图，看似新颖独特、生动直观，但这其实是成人化思维的产物，超越了小学生的认知水平。正六边形的认识及其周长的计算对小学生来说比圆的周长计算要困难得多，属于小学生的未知范畴。用未知来说明未知，不符合小学生的认知规律。

异议三：环节1、2中的直观图都是教师设计好后直接呈现给学生的，这时的学生尽管不是单纯的操作工，但也不是真正意义上的探索者，所以还不能认为是给了学生更多的机会，学生也没有做更大的事情。

那么，如何让学生做大一些的事情呢？笔者认为关键是让学生自主发现、提出和解决两个问题：（1）圆的周长和哪些因素有关？（2）圆的周长和直径到底有什么关系？

第一，在没有任何提示和启发的状态下，让学生开放性地发现和提出问题（1）。学生应该能猜到圆的周长和直径有关。如果学生不能猜到圆的周长和直径有关，教师可画三个大小不一、位置不同的圆来帮助学生思考和发现，然后再把这三个圆通过平移放在一起，变成同心圆（可制成课件），这样就便于学生观察和比较，就能更好地印证学生的发现。至此，问题（1）被学生发现并解决，从而得出结论“圆的周长随着直径的增大（减小）而增大（减小），同时，学生也有了良好的体验和积累了丰富的活动经验。

第二，让学生自由发挥来解决圆的周长和直径到底有什么样的关系的问题。在学生遇到困难时，教师可适时通过以下几种方案进行引导（如学生有此发现，拿来推广最佳）。

1.画出一组圆内切正方形的组合图，通过观察让学生发现：①圆的周长小于边长是直径的正方形的周长，而正方形的周长和边长的比是4。②圆的周长随着直径的增大而增大，而周长和直径的比值小于4。

2.给出三个大小不同的学具圆，将其周长展开后再和直径进行直观比较，让学生自主发现周长是直径的3倍多一点。

由以上不难猜想：圆的周长和直径的比是一个固定的数值（定值），介于3和4之间。剩下的环节按原案例中的3～6环节进行即可。

综上可知，在教学时，教师要认真倾听学生的想法，要给学生留足“折腾”的空间，学生才能做大一些的事情。