追寻刹那间的思维光亮——谈小学数学教学中学生直觉思维的培养

江苏南京市长江路小学（210000）

【教学片段】

师：如图1，平行四边形的面积是24.8平方厘米，阴影部分的面积是多少平方厘米？

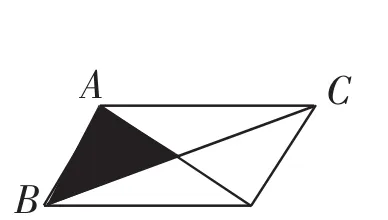
图1

生1：用24.8除以4就能算出。

师：为什么？

生1（迟疑很久）：△ABC的面积是平行四边形面积的一半，阴影部分和△ABC等底，而高是△ABC的一半，所以阴影部分的面积是平行四边形面积的一半又一半，因此除以4。

……

类似的场景不止一次出现过，我注意到这些学生大多都是数学学习的佼佼者，殊不知，他们能如此快地进行判断和论证，其实“数学直觉思维”功不可没。

当前的小学数学教学一直反复强调逻辑思维，总是追问“为什么？”，殊不知，这样却抑制了学生的直觉思维发展。还有一些教师对于直觉思维的认识也存在一定的误区，认为直觉思维是那些创造者的特权，对学生直觉思维中的突发性和非逻辑性存在偏见，觉得没有严密的推理和思考的结果是不科学的。

直觉作为一种心理现象，贯穿于学习、研究和生活中，但是它更倾向于一种“感”，或是一种“悟”，所以直觉思维出现时，思维者对它也没有清晰的意识，在课堂教学中容易被忽视，或者是被错过。

一、把握本质，走近数学直觉思维

关于数学直觉思维，美国教育家布鲁纳认为“直觉是直接的了解或认知”，法国数学家彭加勒认为“数学直觉就是对于数学对象内在的和谐与关系的直接洞察”，我国心理学者朱智贤、林崇德认为“直觉思维是直接领悟的思维或认知”，郑毓信认为“数学直觉是一种直接反映数学对象结构关系的心智活动形式，是人脑对数学对象的某种直接的领悟或洞察”。

一般来说，可以将思维分为逻辑思维、形象思维和创造性思维，直觉思维是创造性思维的重要组成部分。不同于逻辑思维，直觉思维过程不遵循一定的逻辑规则，没有清晰的思维步骤。简单地说，直觉思维是没有严格的逻辑推理的，是直接而快速地理解、思考问题。

我认为，数学直觉思维就是在遇到比较复杂的问题时，能够快速检索自己的知识系统和经验储备，经过整体全面的观察，抓住问题本质，做出猜想并迅速判断和推理，一下子找到解决问题的关键，从而非常快地解决问题。

一般来说，数学直觉思维会表现出如下一些特征。

其一，迅捷性。

面对一个问题，无须考虑和推理，根据自身的知识经验，结合具体情况，立刻做出判断，即运用已有的知识经验，经过整体全面的判断，把握问题的本质。

【案例】“一看就知道。”

题目：31.8×1.31＝（ ）。

A 4.1658 B 41.658 C 40.64 D 416.58

生1：选B。（其他学生惊讶于他的速度）

师：怎么想的？

生1：一看就知道。

生2：怎么一看就知道呢？

生1：答案显然是三位小数啊！其他就可以全部淘汰了。

师：如果答案里还有另一个三位小数，那该怎么办？

生1：末位肯定8，而且三位小数必须大于30小于100。

显然，这个学生能做出快速的判断，是因为他掌握了小数的乘法计算的本质，并且理解小数计算过程中估算的方法，所以整体观察之后就能迅速得到了正确的答案。这里体现的就是数学直觉思维的迅捷性。

其二，跳跃性。

数学直觉思维会带领思考者径直走向最后的定论，这种跳跃性主要表现在想问题时不按部就班地进行，而力求在问题中抓住某些信息就直接解决问题，具有一定的突然性。

【案例】“我有更简单的办法。”

题目：比较2/5和4/7的这两个分数的大小时，应该怎么比？

生1：通分。

生2：我有更简单的办法。拿它俩都和1/2比，得到一个比1/2大，一个比1/2小。

在解决这个问题的时候，学生找到了“1/2”这个思维的支撑点，主要运用的就是分数的数感，体现了数学直觉思维的跳跃性。

其三，偶然性。

【案例】“哎呀，不对！”

题目：商场进行抽奖活动，有3个箱子，如果允许去掉一个空箱子，得奖的可能性会变大吗？

生（齐）：当然了！

师：商场进行抽奖活动，有3个箱子，你任意选一个箱子，然后打开剩下的2个箱子中空的那个，这时如果给你一次换箱子的机会，你换吗？

生1：我不换，因为剩下两个箱子选一个，选中的可能性都是1/2。

（其他学生表示同意）

师：真的不换吗？

生1：哎呀，不对！还是要换！第一次选的时候得奖的可能性是1/3，如果知道了哪个是空箱子并把它去掉，就相当于给你选了两个箱子，所以得奖的可能性是2/3！

数学直觉思维往往都是无意识发生的，有时如闪电一般突然产生，思维者也经常说不出为什么，无法阐述过程和原因。学生由于经验上的差异，会对事物产生不同的直觉，得到的结果也就会有差异，可能是对的，也可能是错的，存在一定的偶然性，最终还是要经过逻辑论证或实践证明。因此，对待学生正确的数学直觉思维结论，教师首先要引导学生思考，找寻理论上的依据，而对于错误的数学直觉思维结论，则要给予恰当的解释，帮助学生分析原因。

其四，创造性。

直觉思维是对研究对象的整体把握，着眼于从整体上揭示事物的本质和联系，是非逻辑性的思维，它是丰富多彩的，是向外发散拓展的，因而有时候是独树一帜的，具有创造性。

【案例】“我知道！”

题目：平行四边形和三角形的面积和底分别相等，平行四边形的底是20厘米，高是12厘米，三角形的高是（ ）。

生1:20×12×2÷20。

生2:我知道！三角形的高是24厘米，是平行四边形的2倍。

这里，生2一反常规思路，根据公式和图形之间的联系，运用敏锐的直觉思维找到了具有创造性的、便捷的计算方法。

二、贴近儿童，走进数学直觉思维

徐利治教授指出：“数学直觉是可以后天培养的，实际上每个人的数学直觉也是不断提高的。”因此，教师要结合直觉思维的特点，关注学生直觉思维能力的培养。

其一，夯实知识储备。

扎实的知识基础是直觉思维产生的源泉，直觉思维并不会凭空产生，首先要有扎实的基础知识和丰富的经验方法。因此，教师要理解学生，设计相应的教学活动，以此提升学生的认知理解水平，促进学生直觉思维的发展。

【案例】原来这么简单！

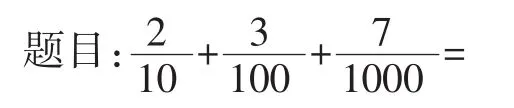
生1：0.237。

师：你怎么算得这么快？算式是分数，你的答案怎么是小数呢？

生1：换成小数算很简单（如图2）。

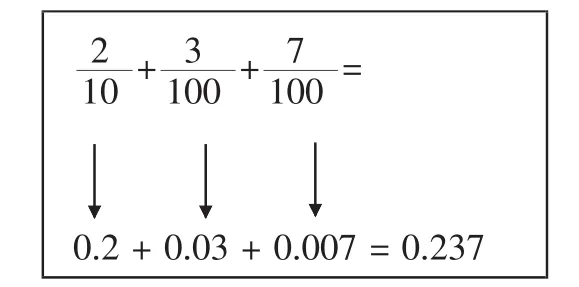
图2

在学习分数和小数的简算时，如果对它们之间的互化、定律、性质等不熟练，没有一定的简算模型，是不可能有如此的直觉思维。因此，教师必须加强基础练习，帮助学生积累学习经验，特别是将知识模块化、结构化。

其二，揭示思维过程。

多数的直觉思维让人短时间内说不出具体的原因和思考过程。教师要引导学生抓住事物的本质和内在联系，指导学生还原直觉思维的过程，把思维跳跃的地方清晰地说出来，从而完善想法，因为好的直觉思维也不是天上掉下馅饼。

【案例】“可以这样想……”

师：怎样求长方体的体积呢？

图3

图4

生1：长×宽×高。用1立方厘米的正方体来铺满它，有几个正方体体积就是多少，只不过数起来有点麻烦。

生2：如果不是正好铺满，这种方法就不行。其实可以把长方体看成“底面积×高”，任意两边相乘都得到一个面，再乘另一条“高”就行。（如图3）

生3：我同意生2的想法，而且我觉得正方体和圆柱的体积也可以这样求。

生4：可以这样想，把那个底面看成小薄饼，高度非常非常小，然后一片一片累积起来，这样体积就是小薄饼的面积乘“高度”。（如图 4）

关于长方体的体积公式，生1仅仅停留在“事实性知识”的层面，生2则达到了“概念性水平”，生3进一步思考，在概念和已有经验之间建立联系，他的理解属于“方法性水平”，而生4所获得的知识已经达到“主体性水平”。在这个有层次的思考过程中，学生的直觉思维也不是无迹可寻的，教师只要坚持展示学生的思维过程，就能帮助学生养成正确直觉思维的习惯。

其三，引导整体观察。

研究表明，借助图形特征解题对培养学生的直觉思维有很大的帮助。

【案例】题目：求 1/2＋1/4＋1/8＋1/16的值。由图5，数形结合可知1/2＋1/4＋1/8＋1/16＝ 1－1/16 ＝15/16。

对于某些情况，由题目的条件和问题得出图形规律或数量关系等，能帮助学生进行跳跃性的思维，提高数学直觉思维能力。对于一些特别复杂的问题，教师要引导学生转换思路，找到关键之处，那么问题就会迎刃而解。

其四，鼓励猜想。

数学猜想是依据数学知识对未知知识或关系做出推理，是一种科学假设。教师应留给学生一些直觉思维的空间，不要急于说出答案，而是让学生在观察整体与局部中发现事物的规律，进而猜想判断。

例如：用转化的策略，能够计算很多平面图形的面积，那么圆形的面积公式是否也能通过转化的策略得出呢？转化成哪种图形最好？猜想并验证三角形的内角和是180°。由一位小数和两位小数的意义猜想三位或多位小数的意义……

图5

其五，提升开放空间。

【案例】“我还有办法！”

师：通过预习，我们知道三角形的面积公式是“三角形面积＝底×高÷2”，能想办法证明这个公式吗？请每个小组至少想出两种不同的办法。

生1：我们把两个完全一样的三角形拼成一个平行四边形，三角形面积就是平行四边形面积的一半。这是把三角形转化成平行四边形。

生2：我在书上看到古人把三角形转化成长方形。实际上就是“1/2底×高”。

生3：我觉得还可以用“1/2高×底”。

生4：我还有办法!可以这样画。（如图6）

师：面积怎么好像变小了呢？

生4：那边叠起来之后是2层，所以还要×2，就相当于“1/2高×1/2底×2”。

巧妙和求异的想法只有在一个宽松、开放的空间里才能得以释放。课堂上，多创设让学生数学直觉思维生长的空间，真正让数学直觉思维生根发芽！

总的来说，教师要及时捕捉学生在学习中出现的灵感，同时，给学生更多的自主权，鼓励学生有自己的奇思妙想，保护学生刚刚萌芽的数学直觉思维。另外，教师应该顺学而教，让学生也能尝试“跟着感觉走”并获得成功的体验。最后，借用斯图尔特曾说过的一句话共勉：数学的所有力量就在于严格性和直觉巧妙地结合在一起，富有灵感的逻辑和控制的精神！

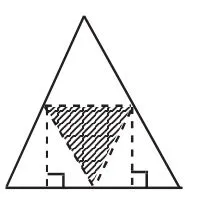
图6

［1］徐立治，王前.数学与思维［M］.大连：大连理工大学出版社，2016.

［2］郑毓信.数学思维与数学方法论［M］.北京：教育出版社,2005.

［3］陈冬梅.小学数学课堂教学培养学生创新能力的探索［J］.小学教学参考，2009（18）.

［4］蒋桂兰.小学数学教学中学生思维能力培养的探索［J］.江苏教育研究，2007（6）.

［5］张宏政.直觉思维与逻辑思维的巧妙结合［J］.数学教学通讯，2007（11）.

［6］潘霖.如何在高中几何教学中培养直觉思维［M］.金华：浙江师范大学，2007.

［7］李铭伟，数学直觉思维在中学数学问题解决中的作用［J］.中学教学参考，2010（17）.

［8］孙红丽.数学直觉思维的培养［J］.新课程，2007（1）.

［9］苏立云.论小学数学直觉思维及其培养［J］.当代教育理论与实践，2009（6）.