内化推理策略 提升思维品质——以“简单推理——数独”的教学为例

浙江杭州市萧山区楼塔镇中心小学（311200）

数独是一种需要玩家根据方格内已知的数，利用规则，推理出所有剩余空格的数的填数游戏。这种游戏十分考验解答者的观察力和逻辑推理能力。本文以“简单推理——数独”（人教版教材二年级下册第110页）的教学为例，谈谈自己的感悟。

一、初次尝试

我上课前的想法是让学生掌握好解决数独问题的一般步骤与方法，并加以拓展应用，从而巩固推理的知识，感受推理的作用，培养学生解决问题、有序思考的能力，进而提升学生的思维品质。

第一次试教时，我处处围绕“掌握解决数独问题的方法”来教，引导学生根据填数规则“（1）每行、每列都有1～4这四个数；（2）每个数在每行、每列中只出现一次。”来解决四个☆处填几的数独问题（如图1），依此形成解决数独问题的策略。

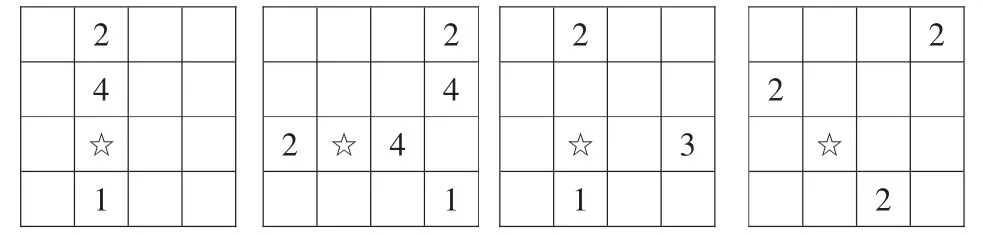
图1

尝试应用环节以同桌两人合作学习的形式，借助上一环节中形成的解决数独问题的策略，先确定图2中☆处填几，最后把整个方格图填写完整，从而深化解决数独问题的策略。

图2

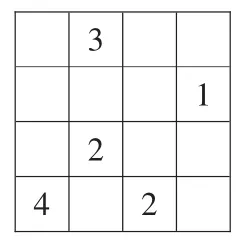
图3

巩固练习环节，学生根据已掌握的解决这类问题的策略，先独立解决图3所示的数独，再同桌交流，最后班级汇报，达到对这种策略的强化和巩固。

整节课存在以下几个问题：

问题一：整节课中，都是我带领着学生学习如何解决具体的数独问题，学生处于被动学习的状态，自然不会积极思考问题。

问题二：整节课中，部分学生跟不上教学节奏，教学不能照顾到接受能力较弱的学生。

问题三：很多时候，学生虽然知道☆处填几，却不能较好地表述自己的推理过程。

问题四：数独，既然是数学游戏，那么该节课的游戏味应有所体现。

带着这些问题，我对该课进行了深入思考，并确定了该课教学的主方向：让学生自创学习素材，并在完善学习素材的过程中，内化推理策略，提升思维品质。

二、再次实践

（一）问题指引，形成学习素材

师（出示图4）：谁能来介绍一下这个图形？把1、2、3、4这四个数填入16个小方格中的任意四个位置，你会吗？请在方格纸上用你喜欢的方法填完。

【设计意图：通过以上两个问题的指引，既复习了“行和列”的知识，又为新课教学提供了来自学生自身创作的学习素材。】

图4

（二）尝试完善，获得推理策略

1.认识规则

师（出示学生作品一，如图5）：这位同学已经把第一行填好了，接下去需要把余下的三行填写完整。不过填的时候，需要满足两个规则：（1）每行、每列都有1～4这四个数；（2）每个数在每行、每列中只出现一次。

师：谁能用自己的话来介绍一下这两个规则？

【设计意图：对填数规则有一个明晰的了解，这对学生后期解决这类问题能起到极大的促进作用，同时有利于指引学生完成该类问题后进行快速检验。】

2.完成第二行——应用填数规则

师：根据这两个规则，第二行可以怎样填？

生1：2、1、4、3。（如图 6）

师：你是怎么想的？

生1：只需要和第一行（对应方格）不一样就行了。

师：还可以怎样填？

【设计意图：该环节是借助规则直接填数，只为让学生再次认识填数规则，并为第三行的填写埋下伏笔。】

3.完成第三行——获得推理策略

师：第三行第一个方格，可以填几？

生2：3。

师：接下去，这行的第二个方格可以填几？

生3：可以填4。上面已经有了2和1，左边也有了一个3，所以只能填4。

师：是的，你观察得很仔细。我们不仅要观察列中出现的数，还要观察行中出现的数。你的回答体现了解决这类数学问题的一个很重要的推理策略：当空格所在的行和列中出现了三个不同的数，它里面只能填剩下的那个数。

图5

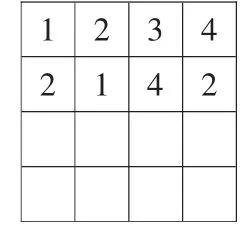
图6

图7

师：请大家齐读这个策略，然后说说这个策略中哪几个字最关键。

生4：三个不同的数。

师：是的，这个策略中最关键的就是“三个不同的数”，它是确定一个位置填什么数的关键信息。我们可以结合这个策略来描述推理过程。因为它所在的行和列中已经出现了 3、2、1，所以只能填 4。

师：如果第一个方格中填4，那么第二个方格又该怎么填？

【设计意图：第三行第二个方格的填写，蕴藏着解决本类问题的关键推理策略——“唯一”解法；又因“语言是思维的外壳”，学生能够清楚地表述推理过程，就能形成思维的逻辑性，所以课堂上不仅要注重推理策略的形成，而且要注重能够利用推理策略表述推理的过程。】

4.完成第四行——运用推理策略

师：现在只剩第四行了，我们可以怎么填？谁来填？

生5：因为每一列都出现了3个不同的数，所以只能填 4、3、2、1。

5.验证作品——小结填数策略

师：我们已经把这位同学的作品补充完整了，接下来请同学们验证每行、每列是否符合规则要求。

师：我们不仅正确地把方格图补充完整了，还发现了一个解决这类问题的一个关键的推理策略，请同学们一起读一读。

【设计意图：完成一个问题后，能回过头去验证是一个很重要的学习习惯，这样能够帮助学生确认解答的合理性和正确性。在小结环节中，特意引导学生验证，并再次强调推理策略，既帮助学生内化推理策略，又培养了学生良好的解题习惯。】

（三）合作解决，巩固推理策略

师（出示学生作品二，如图7）：这位同学是斜着填的。谁能根据刚才的两个规则把第一行或第一列补充完整？

图7

图8

生6：填第一列 3、4、2。（如图 8）

师：接下去哪几个位置可以利用刚才的推理策略优先确定？请把能优先确定的位置圈出来。

图9

师：是的，这三个位置所在的行和列中都出现了三个不同的数，所以能优先确定。接下来，又能优先确定哪几个位置？

图10

师：看来，这个策略在解决这类填数问题时能为我们提供很大的帮助。

【设计意图：“唯一解法”是解决数独问题的一种重要推理策略，而这一策略是需要学生在实际应用的过程中逐渐认识并掌握的。利用推理策略找出能优先确定的位置，使得学生对这一策略能有进一步的认识。】

（四）学生创问，同桌交换解答

1.学生创问

师：刚才我们解决了好多填数问题，请自己创造一个问题，让你的同桌来解决。

师：请在4×4方格纸中，挑选一些空格填上数，然后交由你的同桌把余下的空格填充完整。

2.作品展示

师（出示图11）：请大家一起来验证这位同学的作品是否符合规则。

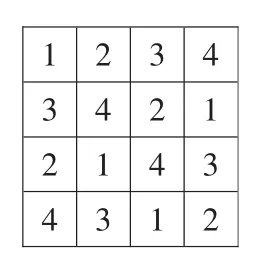
图11

师：这位同学的作品中不光每行、每列，而且每个2×2小正方形中都有1～4这四个数。

3.错例辨析

师（出示图12）：老师发现有一位同学填不下去了，你们认为是什么原因造成的?

师：一开始的问题是怎么样的？老师把它圈出来（如图 13）。

图12

图13

师：第二行第三列所在的空格，还能填吗？

师：在设计问题的时候，需要考虑到填数规则。

【设计意图：让学生经历自己创造问题、同桌互换解决的过程，学生既能感受到数独游戏的乐趣，又能在错例辨析中进一步认识到数独游戏的特点。】

（五）拓展提升，内化推理策略

师（出示问题：把我、爱、数、学这四个字填入方格图中（如图 14）。（1）每行、每列都有我、爱、数、学这四个字；（2）每个字在每行、每列中都只出现一次；（3）每个粗线框内都要有我、爱、数、学这四个字。）：这三个规则大家看得明白吗？谁能来解释第三个规则?

师：这个问题怎么解决？

图14

【设计意图：根据二年级学生的年龄特征，设计了变式练习的运用环节，由此可以使学生进一步掌握解决这类问题的推理策略，也进一步培养学生有序、全面思考问题的意识。】

三、课后感悟

1.重视学生的思维形成过程

试教时，我都是领着学生学习如何解决一个个特定的数独问题，学生处于被动的学习状态，根本不会积极思考问题，提升学生的思维品质也就无从谈起。

改进之后的再次实践中，把解决这类数独问题的策略藏身于学生自主完善方格图的过程中，通过学生的自主发现“列中已经有了2和1，行中有了一个3，所以只能填4”引出该策略，接着在后面环节中深化与巩固，并引导学生用语言表述出推理过程，这样一个推理策略的呈现流程符合学生的认知过程和思维形成过程，不但内化了推理策略，还提升了学生的思维品质。

“语言是思维的外壳”，能够用自己的语言清楚地表达出推理过程，就能有效地培养思维的逻辑性。因此，教师不仅要注重推理策略的形成，还要注重学生利用推理策略表述推理的过程。

2.注视学习素材的呈现形式

学习素材的呈现，可以来自教材，也可以来自学生自身的创造，而后一种呈现形式更能够调动学生的学习兴趣。第二次教学实践中，先将学生一开始完成的作品“把1、2、3、4这四个数填入16个小方格中的任意四个位置”作为学习素材组织新课教学，接着对该作品进行完善，引出推理策略，到之后的“学生创问，同桌互换解答”，整节课都是借助学生的作品进行新课教学，十分贴近学生。

在“学生创问，同桌互换解答”这一环节中，让学生既能感受到数独游戏的乐趣，又能在错例辨析中进一步认识到数独游戏的特点。

3.珍视学生把握规则的能力

每一个数独问题，都有与之相对应的填数规则，学生是否能够准确地了解这些规则，是解决数独问题的首要条件。为此，需要引导学生准确掌握填数规则，运用推理的知识，把握关键信息，找出每个数字的确切位置。

在变式练习时呈现前面问题中没有出现过的第三个规则“每个粗线框内都要有我、爱、数、学这四个字”，使学生进一步掌握解决这类问题的推理策略，也进一步培养他们有序、全面思考问题的意识。