在感悟问题中“玩”数学

浙江省湖州市双林中学

李建潮 (邮编：313012)

问题268(《数学通讯》2016年第9期问题268)已知a、b、c≥0,bc+ca+ab+abc=1，求证：

①

初涉数学，人们是学数学；到了一定的阶段，便开始“玩”数学了，因为数学好玩．人们在“玩”数学中，去更好地理解数学、认知数学和领悟数学．今以问题268为例浅淡“玩”数学．

1 “玩”(问题268之)证明

证法1作为自然证法莫过于等价转换法，①式等价于：

b4c4+c4a4+a4b4+2a4b4c4≤1

②

由题设易见：0≤bc、ca、ab、abc≤1，故而b4c4≤b2c2，c4a4≤c2a2，a4b4≤a2b2，a4b4c4≤a2b2c2．所以，欲证②式成立，只需证：

b2c2+c2a2+a2b2+2a2b2c2≤1

③

事实上，由题设两边平方，便有

1=(bc+ca+ab+abc)2≥(bc+ca+ab)2(因abc≥0)

=b2c2+c2a2+a2b2+2abc(a+b+c)

≥b2c2+c2a2+a2b2+2abc·a

≥b2c2+c2a2+a2b2+2abc·abc

这就证明了③式，从而问题268获证．

评注1从证法1看，问题268宜改进为：已知a、b、c≥0,bc+ca+ab≤1，求证：

①′

评注2从①式与②式的等价性看，发现一组代数等价式：

bc+ca+ab+2abc=1

④

⑤

⑥

(其中实数a、b、c均不为-1)本文的“后劲”亦在于此．

证法2本法给出条件yz+zx+xy≤1的一种“玩”法.

由题设，易得b2c2+c2a2+a2b2≤1．对此技术处理如下：

a2(b2+c2)≤1-b2c2

⟺a4(b2+c2)2≤(1-b2c2)2

⟺a4(b2+c2)2+(b2+c2)2≤(1-b2c2)2+(b2+c2)2

⟺(1+a4)(b2+c2)2≤(1+b4)(1+c4)

于是

=2.

2 “玩”(问题268之)引申

首先，“玩”问题268的一般情形．事实上，由以上两种证法看到，我们已经“玩”出：

已知a、b、c≥0,bc+ca+ab≤1,2≤α∈R，则

⑦

但注意到两种证法皆有一定的可塑性．于是，大胆再“玩”起：

⑧

分析欲证⑧式，(看到)即证：

同问题268的证法1，须只需证：

⑨

“玩”数学发现，事实上，只要将题设两边立方，并注意到代数恒等式：

(x+y+z)3=x3+y3+z3+3[yz(y+z)+zx(z+x)+xy(x+y)]+6xyz

及

x2(y+z)+y2(z+x)+z2(x+y)=yz(y+z)+zx(z+x)+xy(x+y)

便有

1≥(bc+ca+ab)3=b3c3+c3a3+a3b3+3[ca·ab(ca+ab)+ab·bc(ab+bc)+bc·ca(bc+ca)]+6bc·ca·ab

=b3c3+c3a3+a3b3+[ca·ab(ca+ab)+ab·bc(ab+bc)+bc·ca(bc+ca)] +2abc[a2(b+c)+b2(c+a)+c2(a+b)]+6a2b2c2

=b3c3+c3a3+a3b3+[ca·ab(ca+ab)+ab·bc(ab+bc)+bc·ca(bc+ca)] +2abc[bc(b+c)+ca(c+a)+ab(a+b)]+6a2b2c2

由此可知⑨式正确，引申1获证．

评注3据上分析，引申1的一般性、精准性是显而易见的，值得欣慰．

其次，考虑“玩”问题268的“反向”情形．适当改进问题268的条件，且条件参照“评注2”(并注意到④、⑤二式的等价性)．于是，又大胆设想下述“反向”情形：

引申2已知a、b、c≥0,bc+ca+ab+2abc=1，1≤α∈R，则

⑩

也很难奏效．不得已又“玩”起了问题268的证法1(分析法)来……

证明用分析法知，所证⑩等价于：

3≤(2α-2)(aα+bα+cα)+(2α+1-1)(bαcα+cαaα+aαbα)+3(2abc)α

⟹3≤(2α-2)[(aα+bα+cα)+2(bαcα+cαaα+aαbα)]+3[(bαcα+cαaα+aαbα)+(2abc)α] (α≥1)

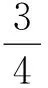
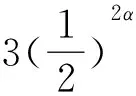
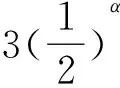
其三，再用Jensen不等式，并注意到题设，有

(bc)α+(ca)α+(ab)α+(2abc)α

⑩

3 “玩”出经典

前面评注2指出：等式④、⑤、⑥是一组代数等价式．下面向读者推荐我们由此“玩”出的几个经典不等式(或组)．

一“玩”条件式⑤：

证明题设两边同乘以bc(1+a)+ca(1+b)+ab(1+c)，并应用三维柯西(Cauchy)不等式，立得

注意到题设⑤的等价式④：bc+ca+ab+2abc=1，知上式即为

再“玩”条件式⑥：

a+b+c≥2(bc+ca+ab)

证明题设两边同乘以a(1+a)+b(1+b)+c(1+c)，并应用三维Cauchy不等式，立得

a(1+a)+b(1+b)+c(1+c)≥(a+b+c)2

即a+b+c≥2(bc+ca+ab)

经典2获证．

三“玩”条件式④：

经典3已知a、b、c≥0,bc+ca+ab+2abc=1

④

证明由④得

1-bc=ca+ab+2abc

同理

以上三式相加，并注意到题设④，得

移项，经典3获证．

评注5经典1的式与经典3的内涵是：

(其中a、b、c≥0,bc+ca+ab+2abc=1)

三角形经典1在锐角△ABC中，有

(cosA+cosB+cosC)2≤2+2cosAcosBcosC

⟺(cosA+cosB+cosC)2≤sin2A+sin2B+sin2C

⟺(cosB+cosC)2+(cosC+cosA)2+(cosA+cosB)2≤3

三角形经典2在锐角△ABC中，有

≥2(cos2A+cos2B+cos2C)

三角形经典3在锐角△ABC中，有

cosA+cosB+cosC≥1+4cosAcosBcosC

本文的确立当归功于①式与②式等价的思维模式，通过思维的不断完善、升华与发散让一个原本名不见经传的问题枝繁叶茂.

数学好玩！