一道初三数学压轴题的研究与教学思考

上海市青浦区实验中学

范莉花 (邮编：638400)

2018年1月，上海市青浦区一模数学压轴题如下：

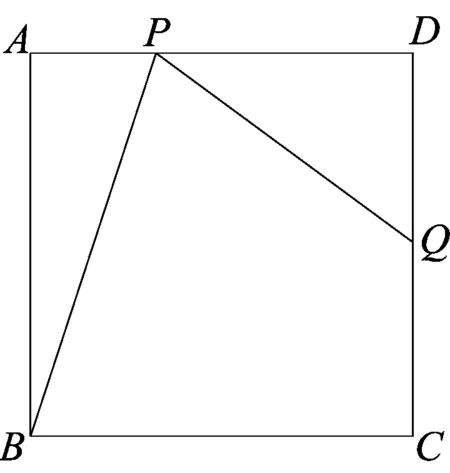
如图，在边长为2的正方形ABCD中，点P是边AD上的动点(点P不与点A、点D重合)，点Q是边CD上一点，联结PB、PQ，且∠PBC=∠BPQ.

(1)当QD=QC时，求∠ABP的正切值；

(2)设AP=x，CQ=y，求y关于x的函数解析式；

(3)联结BQ，在△PBQ中是否存在度数不变的角，若存在，指出这个角，并求出它的度数；若不存在，请说明理由.

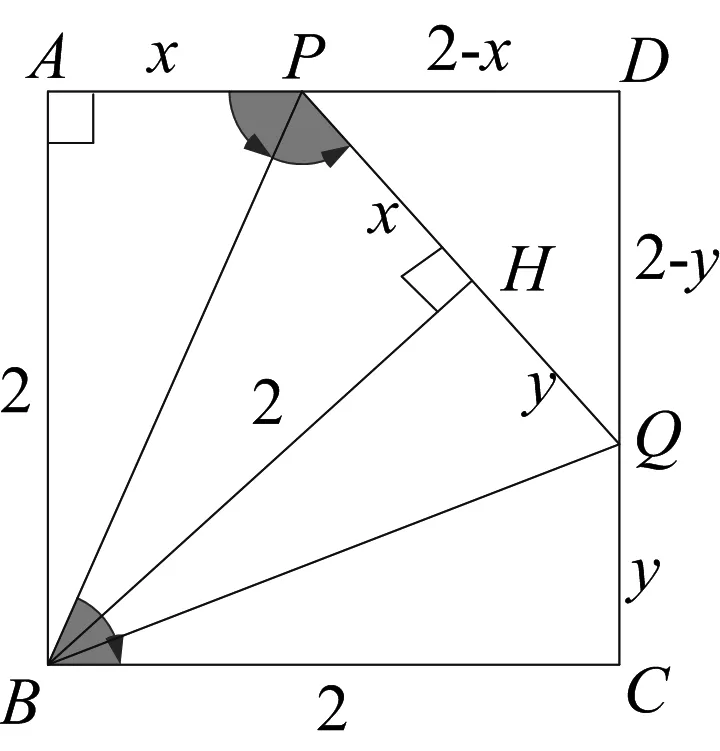
(第一小题是第二小题的特殊情况，解法相同，第二小题解法如下)

解法一(标准答案)过点B作BH⊥PQ，垂足为点H，联结BQ.

易证Rt△ABP≌Rt△HBP和Rt△HBQ≌Rt△CBQ，AP=PH=x，QH=CQ=y，

则PQ=x+y，在Rt△PDQ中，PD2+DQ2=PQ2,

解法二(BH是高,用等积法)过点B作BH⊥PQ，垂足为点H，联结BQ.

易证Rt△ABP≌Rt△HBP和Rt△HBQ≌Rt△CBQ，AP=PH=x，QH=CQ=y，则PQ=x+y，

因∠A=∠C=∠D=90°，BH⊥PQ，故S△ABP+S△PBQ+S△BCQ+S△PDQ=S正ABCD.即

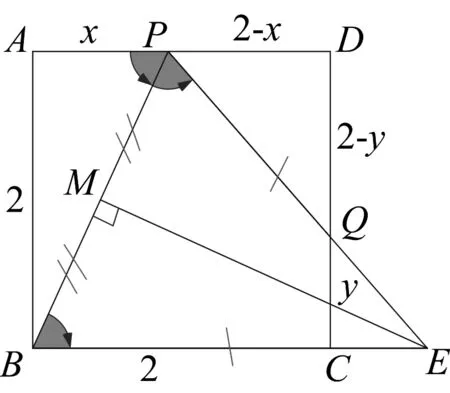
解法三(构造基本型)

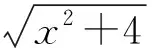
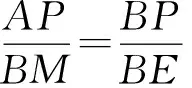
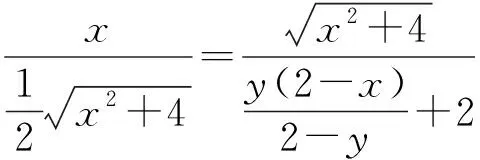
本题的实测结果不尽如人意，14分的压轴题区平均得分只有2.4分，为什么会出现这样的结果呢？压轴题到底有多难？是不是只有优等生才能做？面对压轴题，教师究竟该如何有效教学？

其实，看到此题，不难联想到下面两道题：

1 2010年黄浦区二模压轴题

如图，一把“T型”尺(右下图)，其中MN⊥OP，将这把“T型”尺放置于矩形ABCD中(其中AB=4,AD=5)，使边OP始终经过点A，且保持OA=AB，“T型”尺在绕点A转动的过程中，直线MN交边BC、CD于E、F两点.(如上图)

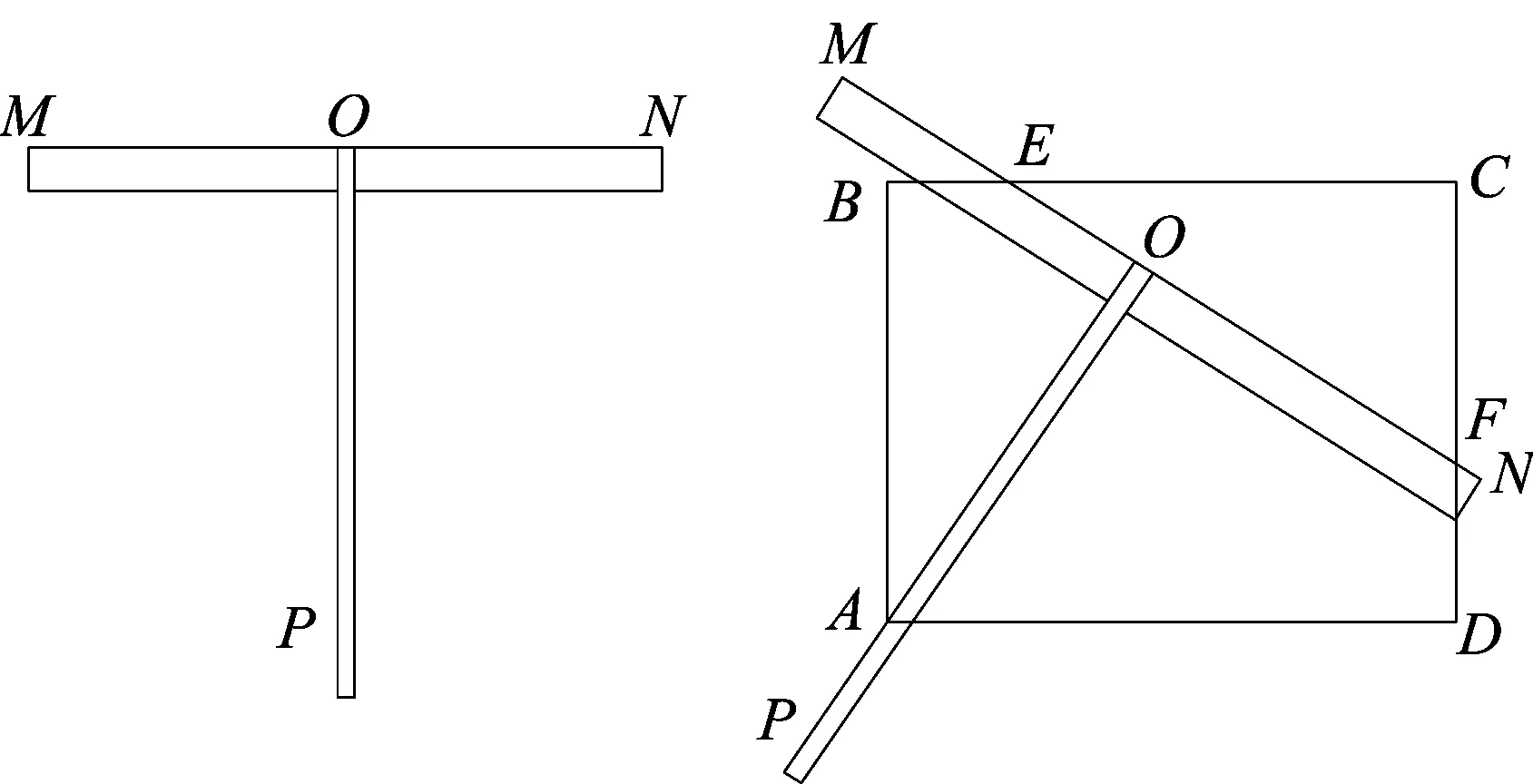
(1)试问线段BE与OE长度关系如何？说明理由；

(2)当△CEF是等腰直角三角形时,求线段BE的长；

(3)设BE=x,CF=y，试求y关于x的函数解析式，并写出函数定义域.

第三小题解法一(标准答案)

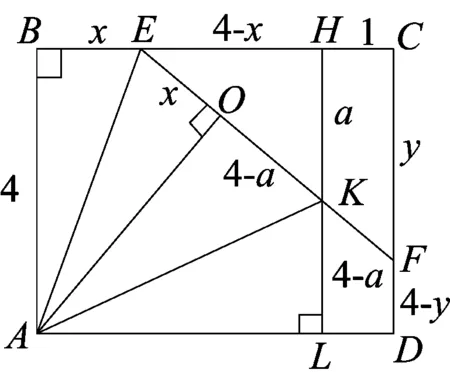
在BC上取点H，使BH=BA=4，过点H作AB的平行线，交EF、AD于点K、L(如图)易知四边形ABHL为正方形，EH=4-x,

易证Rt△ABE≌Rt△AOE和Rt△AOK≌Rt△ALK得BE=OE=x，KL=KO.

令HK=a,KL=KO=4-a，EK=x+4-a,在Rt△EHK中，EH2+HK2=EK2,

因为4-x2+a2=x+4-a2,

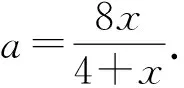
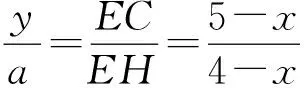
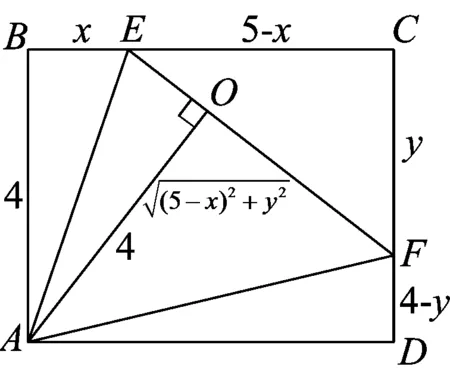
解法二(AO是高：用等积法)

联结AE、AF,得EC=5-x，DF=4-y，在Rt△ECF中，

因∠C=∠B=∠D=90°，AO⊥EF

故S△ABE+S△CEF+S△ADF+S△AEF=S矩ABCD,

(较多学生想到这种方法，但由于整理的过程较为复杂，成为这种解法的“坎”，部分学生最终得不出答案.)

解法三(构造基本型)

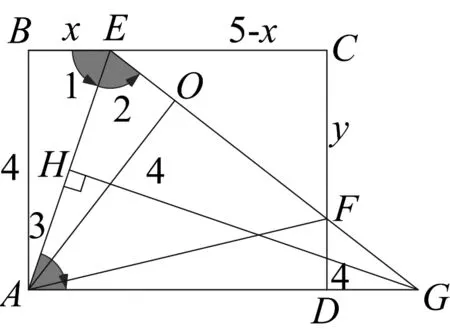
延长EF、AD交于点G，过点G作GH⊥AE，垂足为点H，由∠B=90°.

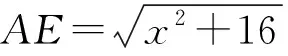
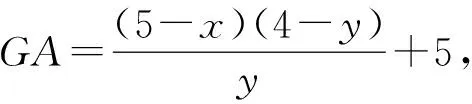
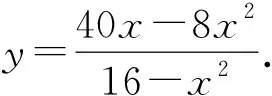
解法四(构造基本型)

过E作EG∥AB，交AO于点G,

由于∠1=∠3，又∠1=∠2，所以∠3=∠2，AG=EG=a，则OG=4-a，∠EOG=90°.

由勾股得x2+(4-a)2=a2

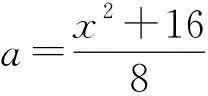
易证∠4=∠5，

所以tan∠4=tan∠5

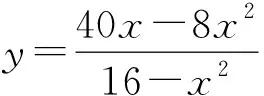
2 2013年上海市中考数学压轴题

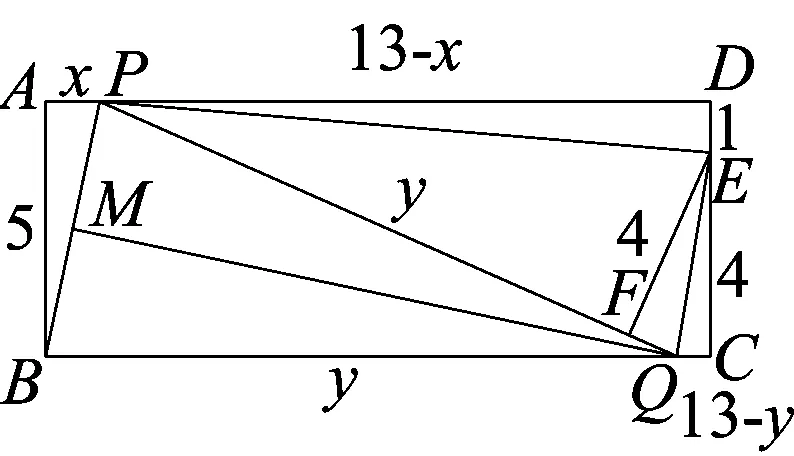
在矩形ABCD中，点P是边AD上的动点，联结BP，线段BP的垂直平分线交边BC于点Q，垂足为点M，联结QP(如图)．已知AD=13，AB=5，设AP=x，BQ=y,

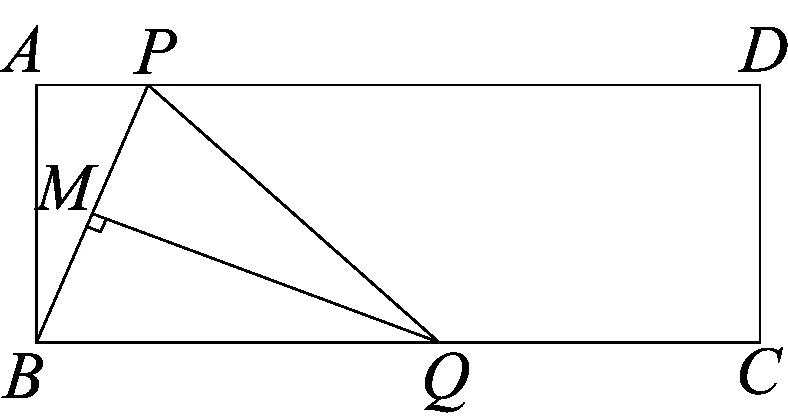
(1)求y关于x的函数解析式，并写出x的取值范围；

(2)当以AP长为半径的⊙P和以QC长为半径的⊙Q外切时，求x的值；

(3)点E在边CD上，过E作直线QP的垂线，垂足为F，若EF=EC=4，求x的值．

第一小题解法(找出基本型)

因为AD∥BC，所以∠APB=∠PBQ

因为四边形ABCD是矩形.

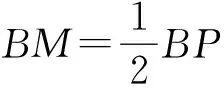
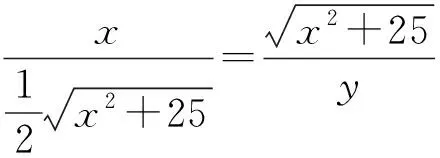
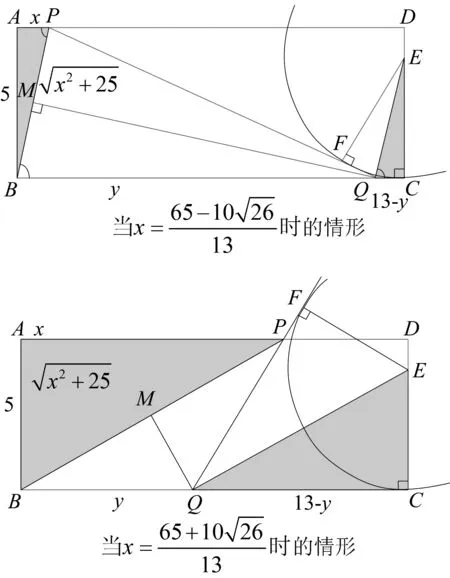
第三小题解法一(标准答案)联接EQ,

因为EC=EF=4，易证△ECQ≌△EFQ

所以∠EQC=∠EQF可得 2(∠DQF+∠PQM)=180°,所以∠EQM=90°,

可得∠EQC=∠PBC=∠APB，

又因为∠A=∠C=90°,所以△APB∽△CQE

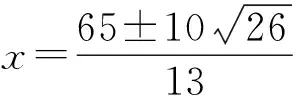
解法二(EF是高：用等积法)

联结PE、EQ,易证BQ=PQ=y，EF=EC=4，DE=1，PD=13-x,

而∠D=∠C=∠EFP=90°，得S△PQE=S梯PQCD-S△PDE-S△ECQ.

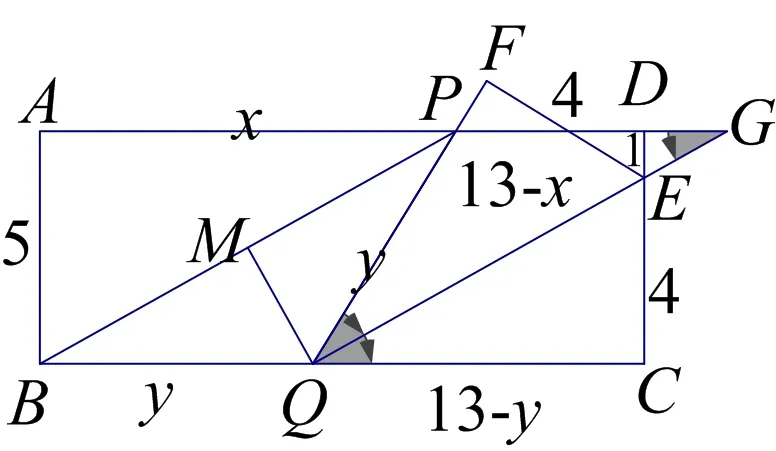
解法三(构造基本型)

联接EQ，延长QE和AD和交于点G.

因为EC=EF=4，所以△ECQ≌△EFQ

故∠EQC=∠EQF,又AD∥BC,

故∠EQC=∠G=∠EQF，

故PQ=PG,又EC=4，DE=1，QC=13-y,AD∥BC,

三个压轴题的比较分析：三个压轴题，时隔8年，虽然有着不同的动态几何背景，但都考查了相似的函数问题，都融合了相似的知识点，都蕴涵着相似的数学思想方法，因此，这三个压轴题有着相似的解题方法.

3 对教学的启示

3.1 按命题背景或解题策略分专题研究压轴题，提高教师“理解压轴题”的能力

数学教育理论界在研究教学问题时有一个潜在假设：凡数学教师，对所教的知识都是了如指掌的，都已具备“理解数学”的能力.然而，大量课堂观察表明，数学教学质量低下的原因，追本溯源，主要来自于教师的数学理解不到位.在日常工作中，确实有教师参考标准答案分析压轴题的现象；更多的是按照备课组教学安排，一题一题认真做题，用多种方法分析压轴题，可往往只是以题论题，缺少分析题与题之间的区别和联系，做不到以题论法；偶尔也会有“考过的压轴题，绝对不会再考，不做也没关系”的侥幸心理.

因此，教师想要有效教学压轴题，必须自身对压轴题理解到位，需要把2008年以来(即二期课改以来)的所有一模、二模和中考的压轴题都认真研究一遍，并按命题背景或解题策略进行专题分类，不仅会做，还要尽量用多种方法做，多与备课组同事交流不同的解题方法，挖掘其中的一些重要的数学思想方法和解题策略，对这些压轴题的解法、区别及联系做到了然于胸，提高教师自身对压轴题的理解能力.

教师只有把解压轴题中的孤立的知识点在大脑中形成知识网络，才能在教学时设置有利于学生理解知识的教学主线，提出具有启发性和挑战性的问题，对学生解压轴题进行针对性、有效性的指导，才有希望培养学生形成真正的独立解决新压轴题的能力.

3.2 按题组进行教学，提高学生分析解决问题的能力，增强学生解压轴题的自信心

在日常教学中，明显感受到学生在解压轴题时有畏难的情绪，常听学生说“我就是不会做”，也常有家长反映，做压轴题时学生对网上的答案有依赖性，所以，如何增强学生解压轴题的自信心，是提高压轴题教学质量关键所在.

比如，教师把三个压轴题作为一组题组进行教学，先教学2018青浦一模压轴题：①学生独立思考问题；②鼓励同学间讨论问题；③教师一一分析不同的解法；④学生用多种方法完善解题过程；再教学2010年黄浦的二模压轴题：①学生独立思考问题；②鼓励同学间讨论问题；③师生共同分析不同的解法；④学生用多种方法完善解题过程，让学生在不同的几何背景中，独立分析出相似的解题方法，巩固上一题的解题策略；最后教学2013年中考压轴题：①学生独立思考问题；②鼓励同学间讨论问题；③让有不同解法的学生自主分析解法；④学生用多种方法完善解题过程，让认真解题的学生能当一回小老师，激发学生探究压轴题的积极性，让学生觉得压轴题也是可以做的、能做的、会做的，最后建立起解题的自信心.而不是孤立地“刷”压轴题，一味地搞“题海战术”，教师应该对压轴题有整体的把握，能系统地思考，站得高才能望得远，找到适当的方法提高学生的解题质量，所以，在教学中，教师需要做到引导学生从“以题论题”到“以题论法”，再到“以题论道”，走出解答压轴题的误区.

著名数学家波利亚指出，一个完整的解题步骤包括：弄清问题、拟订解题计划、实现解题计划和解题回顾四个环节.在解题回顾环节中，学生们可以对解题过程进行总结和反思，回顾每一个步骤的合理性和必要性，对比联想相关的解题思想，长期坚持下去，就有可能升华为解题策略.

通过，上述三题为一组的题组教学，让学生有这样的自信心，只要平时认真、肯下功夫，压轴题是完全能做的.

1 章建跃.理解数学是教好数学的前提[J].数学通报.2015(6)

2 章建跃.中学数学教学概论(第2版)[M].北京：北京师范大学出版社，2008