高考复习中落实数学核心素养的误区及对策

安徽省无为中学

胡 海 (邮编：638400)

2017年新修订的数学课程标准给出六个“数学核心素养”，即：数学抽象、逻辑推理、数学建模、数学运算、直观想象和数据分析.新课标明确“落实立德树人，提升核心素养”是数学学科目标.每年高考遵循考试大纲要求，体现新课标理念，有效地检测考生的数学核心素养.因此落实数学核心素养就是高考复习的关键.

尽管核心素养为高考复习指明了方向，但是还存在一些误区，高三教师应该重视并采取一定的措施，进而提高复习质量.

1 落实数学核心素养的误区

1.1 轻推理抽象

图1

A．△ABC的三边长一定成等差数列

B．△ABC的三边长一定成等比数列

C.△ABI,△ACI,△CBI的面积一定成等差数列

D．△ABI,△ACI,△CBI的面积一定成等比数列

答案：B.

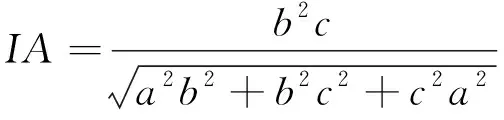
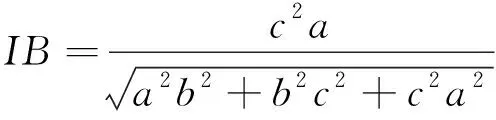
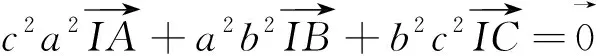
1.2 轻模型建构

例2(2018·常德高三模拟理16)在△ABC中，∠ACB=60°,BC>2,AC=AB+1,则△ABC周长的最小值为______.

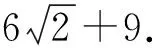
此题学生不会建构关于边长BC为自变量，△ABC周长的函数不等式模型.这次特别将数学建模引入数学核心素养，可见数学建模的重要性.培养学生的建模意识，是高考复习的重要目标.

1.3 轻运算求解

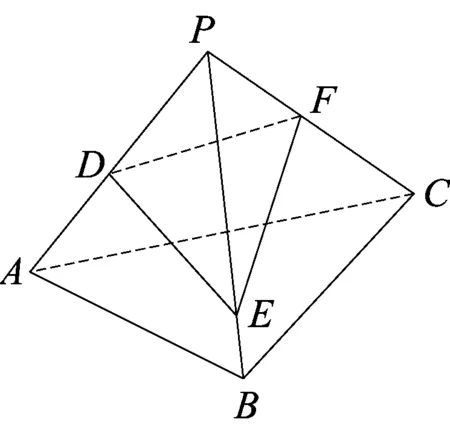
图2

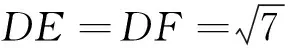
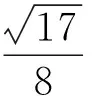
①

②

③

此题对运算求解要求很高，让人望而生畏.再好的思维方法，没有运算能力也枉然.

数学运算是数学活动的基本形式，是得到数学结果的主要手段.通过运算促进数学思维发展，学生能够形成一丝不苟、严谨求实的科学精神.

1.4 轻直观想象

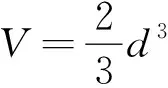
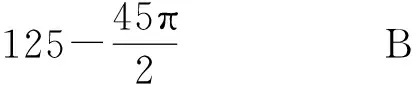
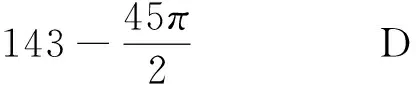
答案：C.

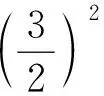
牟合方盖是刘徽构造的一个优美几何体，它是由完全相同的四个曲面构成，相对的两个曲面在同一个圆柱的侧面上，好似两个扣合在一起的方形盖.对牟合方盖的直观图想象不出来，就难求出体积.直观想象是发现和提出数学问题、分析和解决数学问题的重要手段，是探索和形成论证思路、进行逻辑推理、构建抽象结构的思维基础.

1.5 轻数据处理

例5(2018·安庆二模理19)某市有两家共享单车公司，在市场上分别投放了黄、蓝两种颜色的单车，已知黄、蓝两种颜色的单车的投放比例为2：1.监管部门为了了解两种颜色的单车的质量，决定从市场中随机抽取5辆单车进行体验，若每辆单车被抽取的可能性相同.

(1)求抽取的5辆单车中有2辆是蓝色颜色单车的概率；

(2)在骑行体验过程中，发现蓝色单车存在一定质量问题，监管部门决定从市场中随机地抽取一辆送技术部门作进一步抽样检测，并规定若抽到的是蓝色单车，则抽样结束，若抽取的是黄色单车，则将其放回市场中，并继续从市场中随机地抽取下一辆单车，并规定抽样的次数最多不超过n(n∈N*)次.在抽样结束时，已取到的黄色单车以ξ表示，求ξ的分布列和数学期望.

分析本题考查离散型随机变量的分布列、数学期望和数列求和.(1)问主要考独立重复试验事件概率的计算；(2)问一方面求随机变量ξ的分布列，另一方面计算期望时考查了错位相减法.

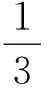
(2)ξ的可能取值为：0，1，2，…，n.则

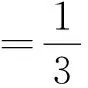
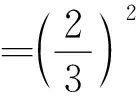
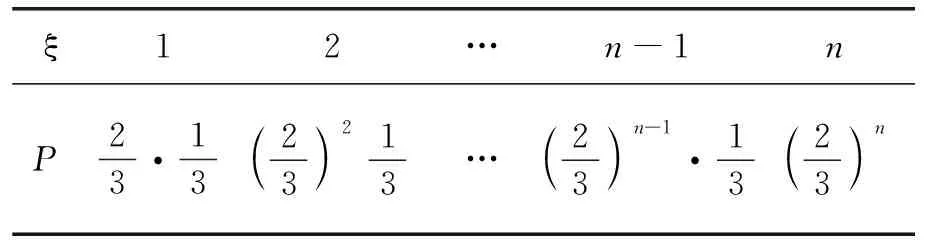
ξ12…n-1nP23·1323 213…23 n-1·1323 n

ξ的数学期望为：

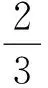
①

②

①-②得：

.

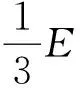
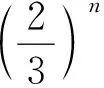
本题是一道考查“几何分布”的概率题，统计概率问题是提升数据分析素养的最有效载体..

2 落实数学核心素养的策略

2.1 夯实基础，落实素养

新课程标准提出课程目标是“四基”、“四能”，即学生通过学习，获得必需的基础知识、基本技能、基本思想、基本活动经验；提高从数学角度发现问题和提出问题的能力、分析问题和解决问题的能力.

案例以导数为例

通过一轮复习，导数专题中的“四基”“四能”基本完成.但在后期的复习中还要加强以下几点：

(1)研究“四大常考函数”.

函数 函数fx=xlnx

函数fx=xex 函数

(2)积累常见“母不等式”：

ex≥x+1,ex≥ex,

(3)常见的题型——含参数不等式成立问题处理方法

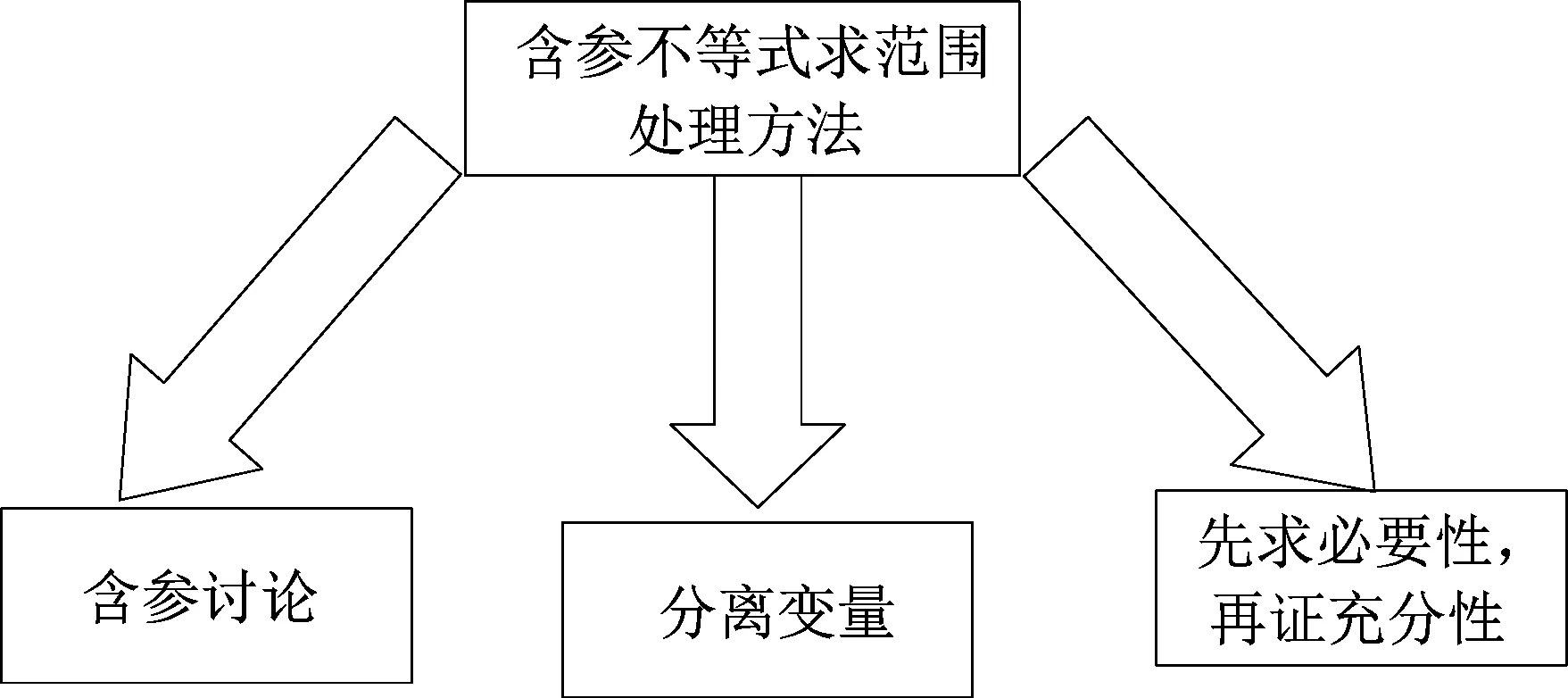
(4)研究导数的奇技巧招：“四大增长函数”的极限、“洛必达法则”、“中值定理”……

2.2 回归课本，落实素养

课本是数学知识、思想、方法的载体,是教学的依据,更是高度智慧的结晶,具有权威性、指导性、规范性.高考复习要充分发挥课本作为提升数学核心素养的作用.

案例以椭圆生成为例

图3

图4

(1)第一定义：平面内与两个定点F1、F2的距离的和等于常数(大于F1F2)的点的轨迹叫做椭圆.

(2)第二定义：

变形得:

图5

由椭圆定义求标准方程过程可得：b2x2+a2y2=a2b2,

图6

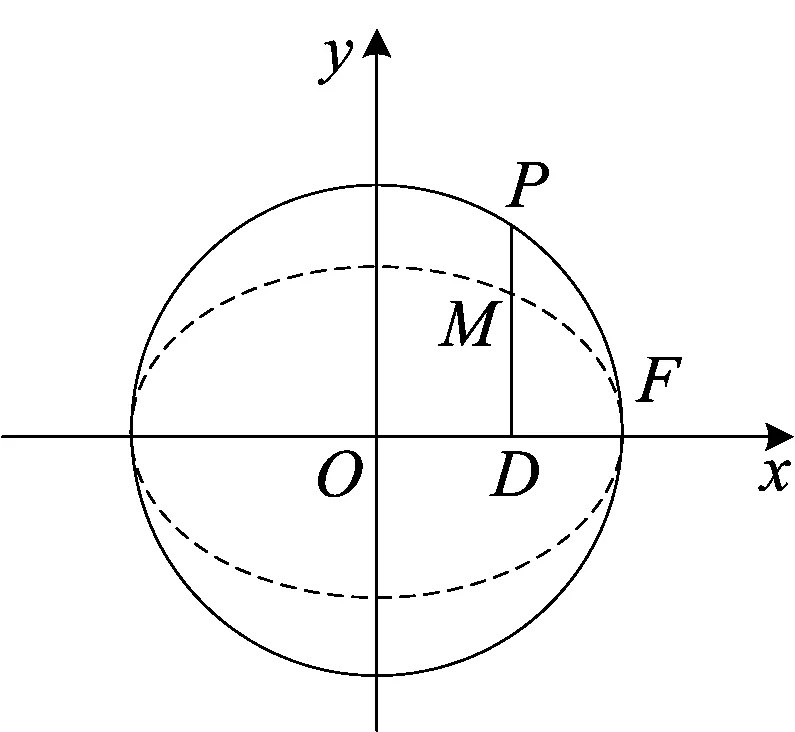
图7

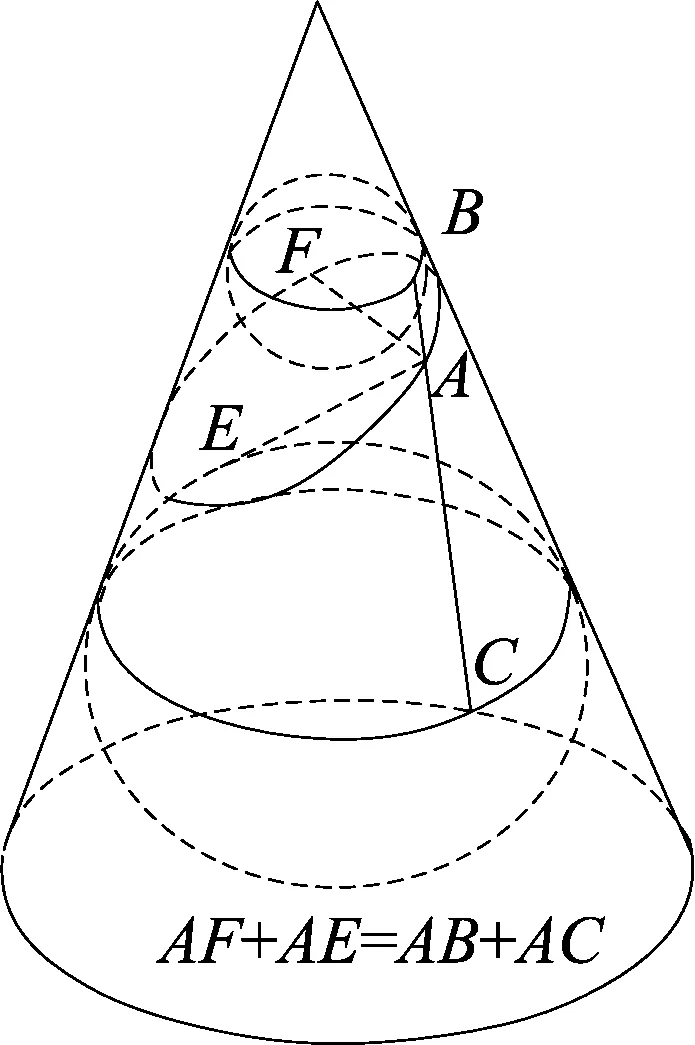
图8

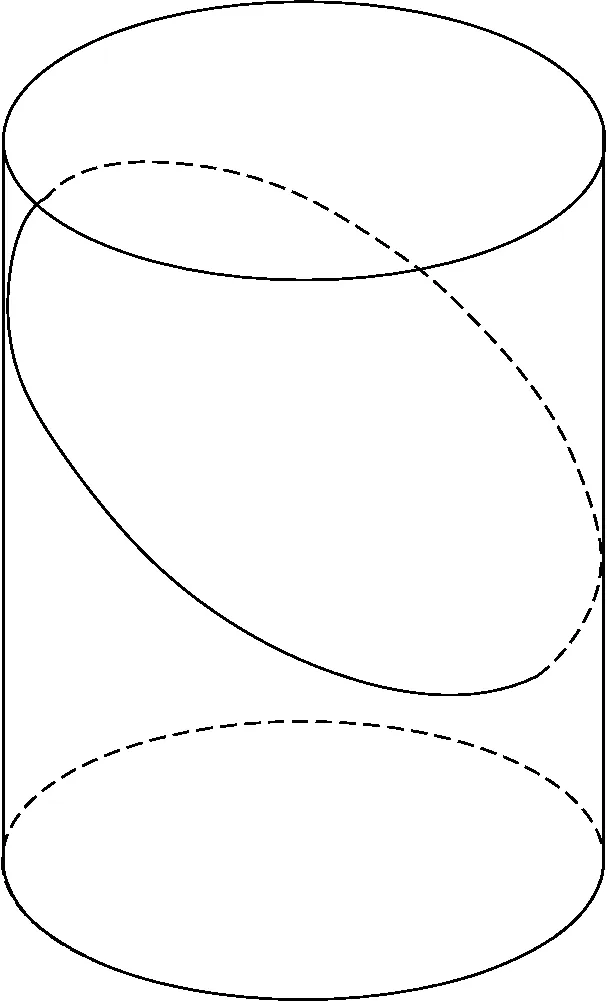
图9

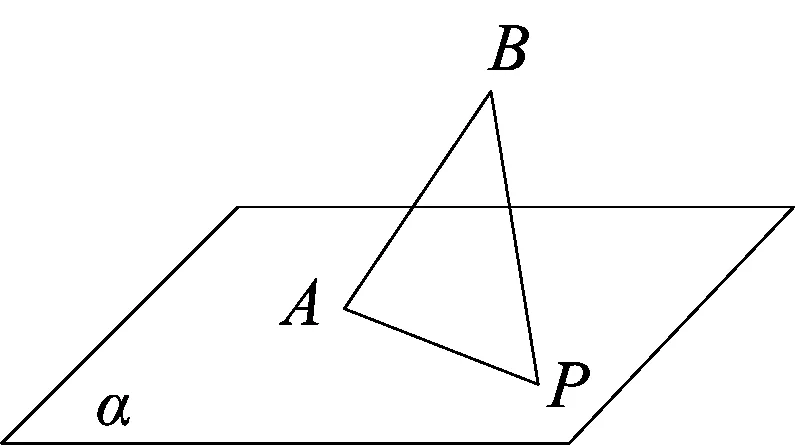
图10

(4)折痕成椭圆(图6)

(5)椭圆与圆的伸缩变化(图7)

(6)动圆与两圆外切、内切生成椭圆

教材上习题：一动圆与圆x2+y2+6x+5=0外切，同时与圆x2+y2-6x+91=0内切，求动圆圆心的轨迹方程，并说明它是什么曲线.

(7)丹德林(Dandelin)双球与椭圆(图8)

(8)平面截圆柱生成椭圆(图9)

链接高考(浙江省高考)如图10，AB是平面α的斜线段，A为斜足，若点P在平面α内运动，使得△ABP的面积为定值，则动点P的轨迹是( )

A．圆 B．椭圆

C．一条直线

D．两条平行直线

△ABP的面积为定值，动点P的轨迹是以AB为轴的圆柱，点P在平面α内运动，则动点P的轨迹是平面截圆柱得的椭圆.

2.3 发散思维，落实素养

波利亚说:“数学是锻炼思维的极好的学科”.通过问题解决，发展学生思维，提升核心素养.

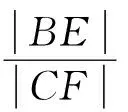
解法1用中线长公式来求解

根据条件3sinC=2sinB,不妨取b=3,c=2,以边a为自变量，建构函数求解.由中线长公式得

.

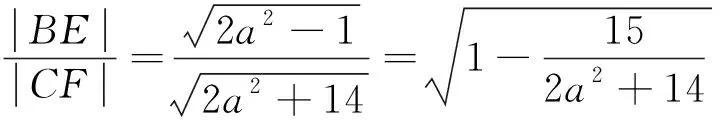
解法2引角求解

.

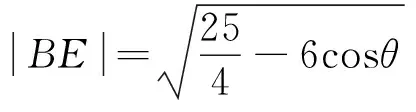
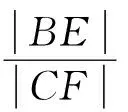
反思三角函数是解决求范围问题的利器.

解法3向量工具求解

不妨取b=3,c=2,设∠BAC=θ,

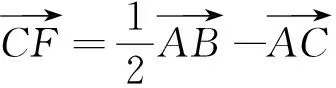
反思向量是高中数学的有利工具，多用向量解题.

解法4坐标化求解

可以A为原点，建立直角坐标系，不妨取b=3,c=2,设C3，0,Bx,y,则由

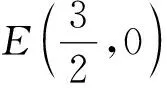
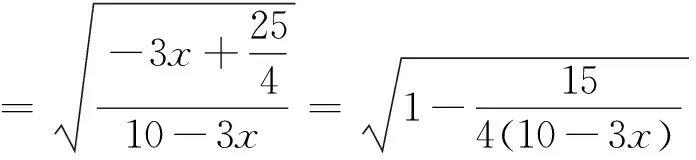
反思解析几何方法是高中数学的通法，几乎能解决所有问题.但遇到困难时，不妨建系设点引入坐标，常常使问题得以解决.

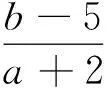
A．-ln3 B．-ln2

C．-1-ln3 D．-1-ln2

这是一道导数压轴题，可一般化求解，但是费时费力.根据逻辑推理，可这样巧解：

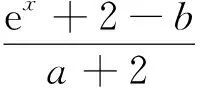
学生的思维水平直接影响其解决问题的能力.在高考复习中，应努力促进学生的思维发展，提升数学核心素养.

结语

落实核心素养教师是关键，教师是参与者、组织者、引导者和促进者.在复习中教师应思正在和将要做的，如：小题狂练的全面性；专题复习的针对性；研究答题细则的规范性和考前指导的实用性等.教师应从“点、线、面”多维度来落实核心素养.“点”是每堂复习课，“线”可以是每一个复习专题，“面”是整个高考复习工作.将点连成线，将线铺成面，全面落实核心素养.

总之，高考复习除了传授数学知识、培养数学能力、领悟数学思想，更重要的是落实数学核心素养，立德树人.

1 李尚志.核心素养渗透数学课程教学.数学通报[J].2018(1)

2 罗增儒.核心素养与课堂研修[J].中学数学教学参考(中旬)[J].2017(8、9)

3 董林.关于勃罗卡点的基本结论及若干推论[J].数学通讯[J].2016(12)