高中数学核心素养评分标准模型初探

华东师范大学数学系

孙 浩 (邮编：200241)

1 研究背景

2014年3月30日，教育部颁布了《关于全面深化课程改革 落实立德树人根本意见》.这是教育部在党的十八大后，关于立德树人根本任务的部署，也是社会发展的必然要求.同时也标志了新一轮基础教育改革的开始.作为数学教育的研究生，对本次的数学课程改革格外关注.其中最为重要的一个环节便是高中课程标准的修订，而此次《普通高中数学课程标准(2017版)》的一个亮点便是高中数学六大核心素养：数学抽象、逻辑推理、数学建模、直观想象、数学运算和数据分析.

这两年随着数学核心素养的兴起，国内关于数学核心素养的研究也是百花齐放，异常丰富.郑毓信(2016)、蔡金法，徐斌艳(2016)、史宁中(2017)等专家也对数学核心素养进行了深入的研究，并给出了具有建设性的建议和看法[2～4].目前国际上关于学习评价模型主要有布鲁姆模型、PISA模型、SOLO模型.

国内关于课程难度的经典模型也有不少，具有代表性的一种是由鲍建生(2002)[5]建立的习题综合难度模型，难度因素分别是推理、运算、背景、知识含量和探究；另一种是由史宁中(2005)[6]提出的从课程时间、课程广度和课程深度三个方面来描述数学课程难度的模型，相比于这类模型如此之丰富，目前国内关于数学核心素养的评分标准模型却很少见.

2 数学核心素养测试卷编制的标准

我们想要尝试着提出数学核心素养的评分标准模型，而这里有个前提，我们必须有一份科学合理的测试卷.通过这张测试卷，我们希望能够最大限度反映出学生数学核心素养水平，所以我们希望测试卷的构成能够以解答题为主，之所以希望以解答题为主，是为了能够观测出学生的解题过程，避免了客观题(如选择题，填空题.只有正确和错误这两种情况.而同时测试卷的选题也需要具有一定的标准，必须科学地包含六大数学核心素养.因此我们依据的选题标准如表1：

表1 测试题制定标准依据

3 测试题数学核心素养水平划分的标准

根据高中数学核心素养水平划分，我们要将测试题所包含的数学核心素养水平作出如下的梳理：(1代表水平一、2代表水平二、3代表水平三)详见[7].例如表2：

表2 测试题数学核心素养水平

通过这样的梳理，我们可以很清晰地观测出测试卷的构成，以及每道测试题所包含的相关数学核心素养(一般情况下，我们认为是测试题所包含的最重要的两个数学核心素养)，通过这样的梳理我们很自然地发现测试卷里同样分值的两道题目，如1和5，都是8分，它们所对应的数学逻辑推理核心素养分别为1、3.如果只是用考生的卷面得分去代表他们的数学逻辑推理核心素养的得分，这显然是不科学的，因此这就需要我们去制定一个相对科学的数学核心素养评分标准模型.

4 数学核心素养评分标准模型

由于不同的数学题里包含的数学核心素养的层次有所差异，因此这就需要我们制定一个评判数学题的数学核心素养评分标准模型.当然，如何做出一个客观的评分标准模型也绝非易事，在此提出几种关于数学核心素养评分标准模型，希望能够抛砖引玉.

4.1 学生数学核心素养表现层次的划分模型

我们以数学抽象核心素养为例，首先我们筛选出所有包含数学抽象核心素养的测试题，并根据这些测试题的分值，计算出总值p,

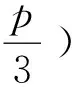
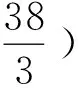
为A层次.显然这样的划分适用于按模块分类，将一张测试卷依照6个数学核心素养分为6个部分，通过这个模型可以量化学生在各个核心素养上的表现层次的比重；也可以运用于不同的对象(学校与学校，地区与地区等)之间的比较.

4.2 测试题学生数学核心素养评分标准模型

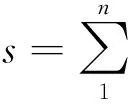
5 案例分析

例如测试题中有一道题目如下：

在一些城市中，街道大多是相互垂直或平行的，从城市的一点到达不在同一条街道上的另一点，常常不能仅仅沿直线方向行走, 而只能沿街走(转直角弯).因此可以引入直角坐标系，对给定的两点A(x1,y1)和B(x2,y2),用以下的方式定义距离：d(A,B)=|x1-x2|+|y1-y2|(注：下述问题中提到的距离都是指上述距离).

(1)证明：对任意的三点A、B、C，满足d(A,B)≤d(A,C)+d(B,C)；

(2)画出到定点O(0,0)距离为1的点P(x,y)构成的图形，并表述图形的特征；

(3)设A(-1,0)、B(1,0),画出到A、B两点距离之和为4的点P(x,y)构成的图形，并表述图形的特征.

这道题目反映出了现实生活中的一种特殊的距离.这与学生们平常所学的欧氏距离有所区别.这需要学生能够理解“街道”距离的定义，规则，并通过这种规则去证明和讨论一些基本的数学问题，着重考查了学生的逻辑推理数学核心素养，(2)、(3)两问同时也考查了学生的直观想象核心素养.在这里我们以(3)为例.

以下是部分测试者的答案：

A同学：

B同学：

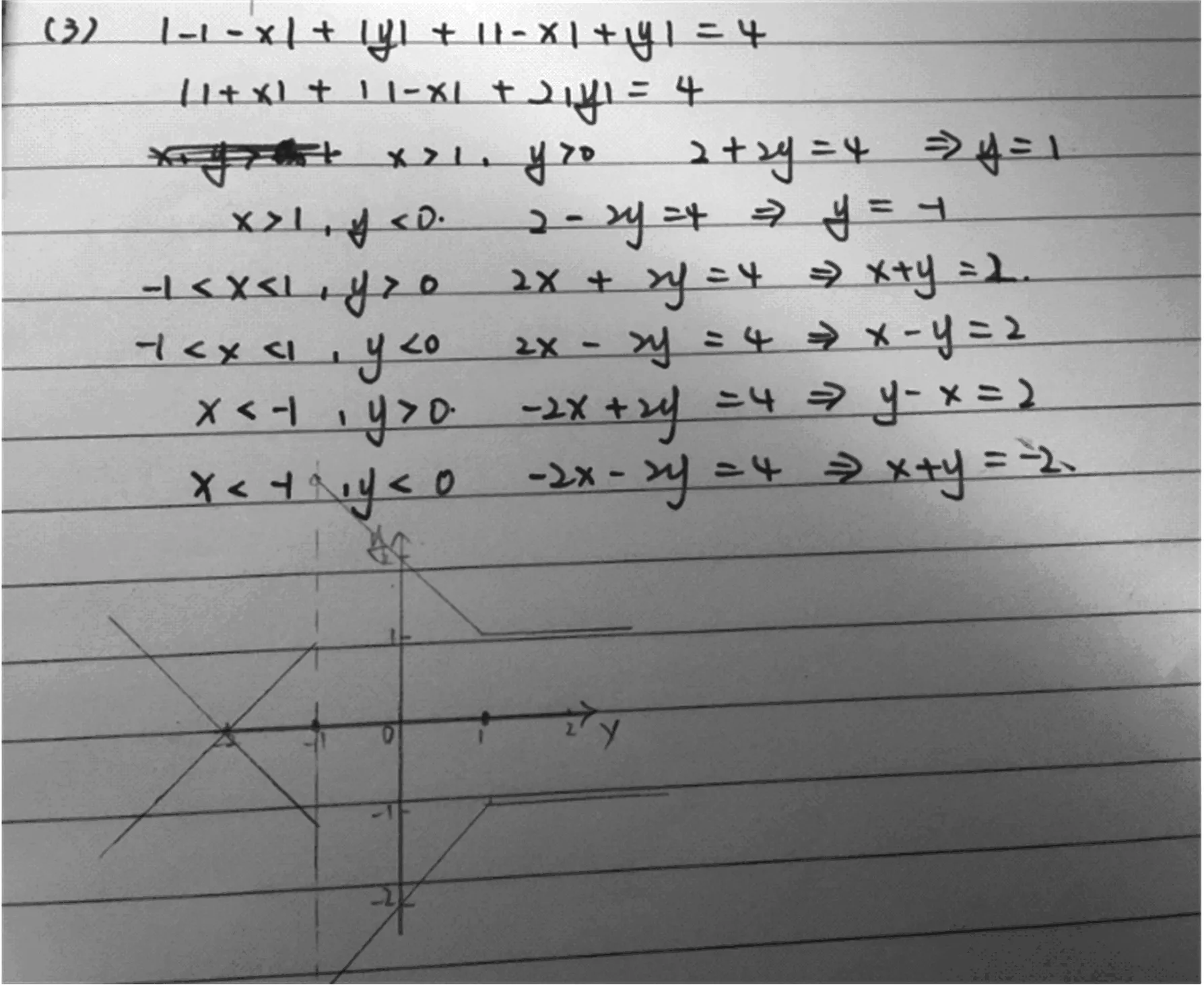
C同学：

D同学：

显然这四种答案的数学核心素养的层次是不一样的，这就需要我们制定较为科学合理的答案，我们可以将其答案分为四个步骤：

1空白或完全错误0″………………………………2能够列出代数式,但是化简错误,导致画图错误2″………………………………………………3画出正确的图形,但没有相应的代数证明;代数证明完全正确,但没有画出正确的图象4″………4图形正确,代数证明正确6″………………………

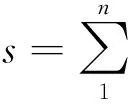
1 核心素养研究课题组.中国学生发展核心素养[J].中国教育学刊,2016,(10):1-3

2 郑毓信.数学教育视角下的“核心素养”[J].数学教育学报,2016,25(3)

3 蔡金法,徐斌艳.也论数学核心素养及其构建[J].全球教育展望,2016,(11):3-12

4 史宁中,林玉慈,陶剑,等.关于高中数学教育中的数学核心素养——史宁中教授访谈之七[J].课程·教材·教法[J],2017.37(4):8-14

5 鲍建生.中英两国初中数学期望课程综合难度的比较[D].华东师范大学,2002

6 史宁中.课程难度模型:我国义务教育几何课程难度的比较[J].东北师大学报(哲学社会科学版),2005,(6):151-155

7 中华人民共和国教育部制定.普通高中数学课程标准(2017年版)[M].北京:人民教育出版社,2017