一个六元分式不等式的证明——兼擂题(114)的解答

重庆市长寿龙溪中学

吴 波 (邮编：401249)

《中学数学教学》2017年第6期擂题(114)是万惠华先生提供的一个优美的六元分式不等式：

我们将证明这个擂题．先给出一个引理．

其中36x4-168x3+253x2-169x+96=1-x36x21-x+96x2-121x+48+48>48>0．

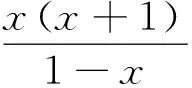
擂题114的证明原不等式⟺

≥3a+b+c．

①

(1)当a、b、c能构成三角形(包括一边等于另两边之和这种退化情形)时，设2p=a+b+c，则p-a，p-b，p-c非负，而ax+by+cz=p-ay+z+p-bz+x+p-cx+y．而由Cauchy不等式知：

令a=y+z，b=x+z，c=x+y(此处的x、y、z不是擂题中的x、y、z)，因为a、b、c能构成三角形(包括退化的)，则x、y、z为非负数且其中至多有一个为0．

结合引理知，只需证：∑-36x4+96x3-61x2+35x≥24即可．

因∑x=1，将上式齐次化，即证：-36∑x4+96∑x3∑x-61∑x2∑x2+11∑x4≥0．

将其配方得：10∑x2x-yx-z+28∑xyx-y2≥0．

结合Schur不等式可知：上式显然成立！因此此时原不等式成立．

(2)当a、b、c不能构成三角形时，不妨设c>a+b．

令c′=a+b，因此存在k>0使得：c=c′+k．此时

②

结合②式知：①式左边

③

④

现在我们要证明③式中的后两项之和大于3k．事实上，我们有(注意c′=a+b)：

⑤

由③式并结合④、⑤两式知：

①式左边>3a+b+c′+3k=3a+b+c．因此此时原不等式成立．

综合(1)、(2)可知擂题(114)的结论成立．证毕．

另外，在情形(1)的证明中我们还得到了如下结论：

注对一边等于另两边之和这种退化情形仍成立．

1 万惠华．有奖解题擂台(114)[J]．中学数学教学，2017(6)：封底.