说题:多维视角下解析一道高考试题
浙江省宁波中学
傅 婷 (邮编:638400)
笔者有幸参加宁波教研室组织的高中数学说题比赛.在参加比赛之前,笔者的学生问了这样一个问题:已知一个抛物线型的酒杯,杯口宽4cm,杯深4cm,若将一个玻璃球放进酒杯中,当玻璃球的半径在什么范围内,玻璃球一定会触及酒杯底部?笔者在给学生解答的过程中,发现这个酒杯中的数学与2016年浙江高考理科数学试卷第19题其实是同一类型的问题.遂选择了这个题目进行说题,题目如下:

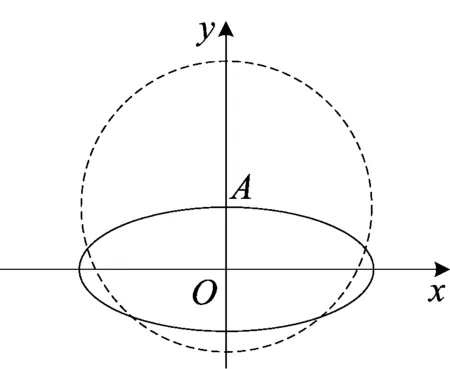
(I)求直线y=kx+1被椭圆截得的线段长(用a、k表示);
(II)若任意以点A(0,1)为圆心的圆与椭圆至多有3个公共点,求椭圆离心率的取值范围.
1 解法分析
考点弦长公式;圆与椭圆的位置关系;椭圆的离心率
几何条件含参圆与椭圆至多有三个交点;离心率范围
目标动态圆锥曲线交点问题的转化

.

第(II)题:考查的是双二次曲线的交点问题,本题中有动态和恒成立两个难点,故问题的解决关键在于交点问题的转化.
视角一代数视角
由于圆锥曲线的交点个数可以转化为方程有解问题,便有解法1.
解法1方程在区间上根的分布问题

(a2-1)y2+2y+r2-1-a2=0
(*)
先考虑有四个交点情况,则需要方程(*)在(-1,1)上有两不同根,由


知识圆与椭圆的对称性、根的分布问题
策略正难则反
思想方程思想
方程的有解问题可以转化为函数的交点问题,故有解法2.
解法2函数在区间上的交点个数

(1-a2)y2-2y+1+a2=r2.


当a2>2时,圆与椭圆有4个不同的公共点.
思想函数与方程思想、数形结合思想
视角二几何视角

椭圆具有对称性,要保证圆与椭圆至多有3个公共点,则圆与椭圆y轴单侧不可能有2个公共点,即弦长在y轴单侧处处不相等.将两条动态曲线的交点问题转化为弦长问题,再代数解决.
解法1弦长相等(浙江省考试院提供的参考答案)
假设圆与椭圆的公共点有4个,由对称性可设y轴左侧的椭圆上有两个不同的点P、Q,满足AP=AQ,记直线AP、AQ的斜率分别为k1,k2,且k1,k2>0,k1≠k2.







①

因此,以点A(0,1)为圆心的圆与椭圆至多有3个公共点的充要条件为1 知识圆与椭圆的对称性、弦长公式 思想函数与方程思想 在解法1的基础上,若AP=AQ,则三角形APQ为等腰三角形,连接PQ,取其中点M,连接AM,如图所示,则AM垂直PQ.涉及中点、垂直的位置关系,可以考虑用点差法,将弦长相等的数量关系转化为几何的位置关系. 解法2点差法 即(x1-x2)(x1+x2)+a2(y1-y2)(y1+y2)=0,得 ② 由AP=AQ,得AM⊥PQ,即 知识圆与椭圆的对称性、点差法 思想设而不求思想、函数思想 视角三函数视角 圆与椭圆至多有3个公共点,即当点P从上定点逆时针旋转到下定点时,PA处处不相等,即弦长在y轴左侧单调.可以考虑构造函数,将交点问题转化为函数的单调性. 解法1弦长在y轴单侧单调递增 知识弦长公式、单调性 思想函数思想 在解法1的基础上,弦长单调递增,即意味着弦长是具有最大值的.反思解法1,利用弦长公式构造出的函数,较为复杂,不便于研究.点P为椭圆上的任意动点,可以利用椭圆的方程进行三角换元来设点P的坐标,则PA为P、A两点间的距离公式. 解法2弦长的最大值 圆与椭圆至多有3个公共点,即当点P从上顶点逆时针旋转半圈到下顶点时,PA单调递增,即当且仅当点P(acosθ,sinθ)为下顶点B(0,-1)时,PAmax=2. PA2=a2cos2θ+(sinθ-1)2=(1-a2)sin2θ-2sinθ+1+a2,(-1≤sinθ≤1) 因为PA的最大值当且仅当sinθ=-1时取到,且1-a2<0, 知识距离公式、二次函数最值 思想函数思想、数形结合思想 对于一个复杂的动态圆锥曲线的交点问题,若直接处理起来比较困难,有时候可以考虑特殊位置. 视角四特殊视角 若需满足题目条件,只需当临界情况,即半径r=2时,椭圆完整在圆内,否则只需半径再大一点就会有4个交点. 策略考虑临界位置 思想函数思想、数形结合思想 解法小结对于本题,解法众多,但笔者认为最理想的解法是转化为距离(弦长)的最值. 本题所涉及的动态圆与椭圆的交点问题,其本质是y轴上的定点A到圆锥曲线椭圆上动点P的距离PA的最值问题.解决步骤如下:(1)两点坐标;(2)距离公式;(3)构造函数;(4)函数最值.深入研究本问题,还是得到一些其他的结论:在y轴单侧,PA单调递增时,圆与椭圆的交点个数为2或1或0个;在y轴单侧,PA不单调时,圆与椭圆的交点个数为4或3个. 以下两个问题也是定点到圆锥曲线(椭圆、抛物线)上动点的距离的最值问题. 有一种酒杯的轴截面近似一条抛物线,杯口宽4米,深8米,称之为抛物线酒杯,当玻璃球的半径为多大时,玻璃球一定会触及到酒杯底部. 对于2016年浙江高考理科数学试卷第19题,定点A在y轴上的位置比较特殊,恰为椭圆的上顶点,故对这个问题还可以进行拓展. 变式1点A在y轴上,椭圆外 变式2点A在在y轴上,椭圆内 变式3点A在y轴正方向上运动 解设椭圆上动点为P(acosθ,bsinθ),则 PA2=a2cos2θ+(bsinθ-tb)2=(b2-a2)sin2θ-2b2tsinθ+t2b2+a2,(-1≤sinθ≤1), 变式5点A在x轴正方向上运动 解设椭圆上动点为P(acosθ,bsinθ),则 PA2=(acosθ-t)2+b2sin2θ=(a2-b2)·cos2θ-2atcosθ+t2+b2(-1≤cosθ≤1), 一般结论: 变式6圆与抛物线的交点问题 设抛物线方程为x2=2py(p>0),若任意以点A(0,t)(t>0)为圆心的圆与抛物线至多有3个公共点,求t、p需满足的条件. 变式7点A为平面上任意一点 通过对这道高考试题的研究,笔者得到了一些启发.任何一个复杂解析几何问题的解决,都需要用到基本知识,因此在教学的过程中应该注重学生基础知识、基本技能的夯实;引导学生从不同视角下进行研究,挖掘问题的本质;关注解析几何问题(比如交点问题)转化中的通性通法,方程与函数、数形结合等思想的应用.通过对问题的变换、推广和转化,可以有效培养学生思维的广阔性.



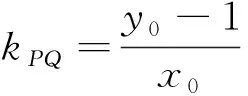













2 背景分析
2.1 本质研究
2.2 问题链接

3 拓展变式







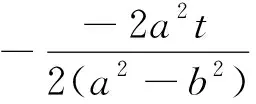





4 教学启示

