智能车辆换道行驶的经济车速研究∗

金 辉，丁 峰

(北京理工大学机械与车辆学院，北京 100081)

前言

智能车辆是集感知定位、规划决策和运动控制等功能于一体的复杂智能控制系统[1]。随着计算机、人工智能和传感器等关键技术的飞速发展，智能车辆技术的发展也取得了巨大进步，这对于提高车辆的智能化水平、改善交通安全性和提高燃油经济性等，具有重要的现实意义，同时将对智能交通和节能减排等方面做出重大贡献。

智能车辆技术主要包含辅助驾驶和自动驾驶两个方向。当前对于智能车辆发展的研究思路主要分为两种:一类是以谷歌、百度为代表的互联网企业，凭借其电子地图和传感器技术等优势直接进行完全自主的自动驾驶车辆的研发；另一类是传统的汽车行业，考虑以辅助驾驶为主，逐步推动自动驾驶的实现。例如，2014年5月，谷歌发布了第三代无转向盘、油门与制动踏板的自动驾驶汽车，累计行程超过100万英里，极大推动了自动驾驶技术的发展。国内百度推出的自动驾驶汽车，于2015年12月在国内首次完成了城区及高速路况下的自动驾驶。而传统车企走的是循序渐进的路线，如奥迪A7实现了车速在64km/h下的车道保持和自主车速控制技术。沃尔沃也进行了智能车辆的自动驾驶测试和展示。国内上汽开发的第二代名爵IGS实现自动巡航、车道保持、车辆换道和自主超车等辅助驾驶功能[2]。一汽等企业也相继推出了智能车辆发展战略。目前智能车辆正处在大力发展时期，根据美国汽车工程师学会对汽车自动化层次分级，可以预计到2020年左右，智能汽车可实现全工况自主驾驶[3]。

但智能汽车要从满足“功能”要求向满足“性能”需求突破，不仅要保障智能汽车在各工况下的安全行驶功能，更要提高其在复杂行驶条件下的经济性。《中国制造2025》明确要求，到2020年，掌握智能辅助驾驶总体技术和各项关键技术；到2025年，掌握自动驾驶总体技术和各项关键技术，综合能耗较常规汽车降低10%以上，减少排放20%以上[4]。

在智能汽车的经济性优化控制技术研究中，文献[5]中指出，在正常的交通流下，ACC减少了44%～52%的加速度标准差，验证了节约燃油的可行性。文献[6]中通过仿真进一步说明，减少加速波动的混合交通流可减少约8%的总燃油消耗。文献[7]中提出了一种基于雷达、机器视觉和GPS等融合信息实现混合动力系统分层预测控制的方法，该方法基于制定的最优巡航轨迹，采用模型预测控制算法，可减少燃油消耗达5%。文献[8]中探究了一种能在智能汽车中应用的新型的燃料经济优化系统(FEOS)，通过车辆参数和环境变量输入，利用Lagrange算法得到车辆最佳加减速度，结果验证该系统可节省燃油达20%左右。

综上所述，智能汽车性能的提升，不仅仅是单一性能的提升，而是安全性、经济性等在复杂行驶条件下的协同提升。然而，目前关于智能车辆技术的研究大多集中在主动安全性方面，而对经济性的研究尚处在探索阶段，特别是未考虑不同行驶条件(直道行驶和换道等)下道路因素对车辆燃油经济性的影响，而这些因素极大影响车辆燃油消耗[9]。特别是，对车辆换道经济车速问题尚未得到深入研究。

本文中提出了基于换道轨迹道路曲率信息的车辆经济车速研究方法，实现智能车辆在换道过程中的燃油经济性最大化。在建立瞬态燃油消耗模型和车辆动力学模型的基础上，利用动态规划算法求得车辆在换道过程中的经济车速轨迹。通过Matlab/Simulink与CarSim联合仿真验证所提算法的有效性，最后对实验结果进行分析与总结。

1 换道经济车速问题

车辆通常以稳态经济车速在直道上行驶，当需要执行换道任务时，车辆提前规划出换道轨迹，根据换道轨迹道路曲率大小，进行换道经济车速优化，如图1所示。假设驾驶员可按期望速度行驶，道路中没有交通信号灯和其他车辆的干扰，车辆能从高精度电子地图中获得前方道路属性数据，从而提前规划好换道轨迹路线，进而基于瞬态燃油消耗模型和车辆动力学模型，利用动态规划算法得到换道过程中的经济车速轨迹。该车速可作为目标车速发送至车速控制系统，实现期望车速跟随，从而实现智能车辆在换道过程中燃油经济性最大化。

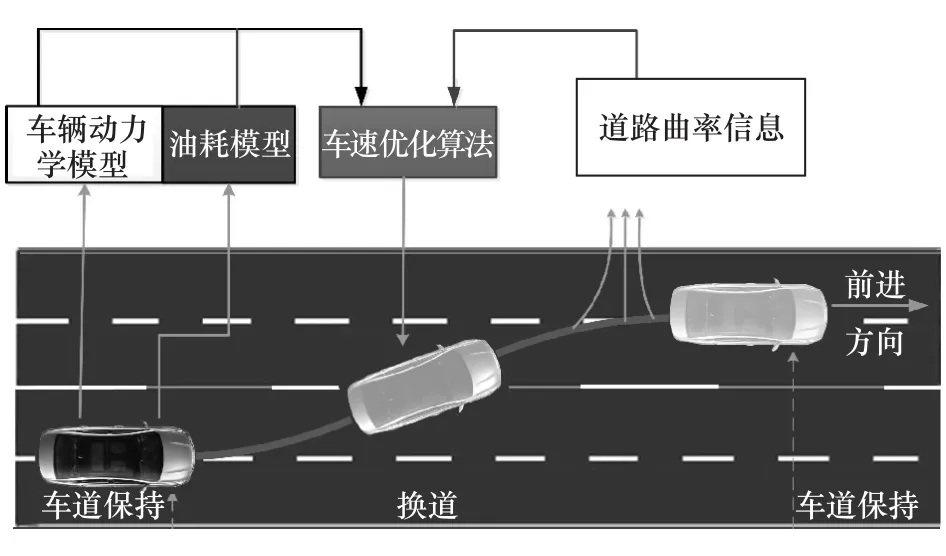
图1 车辆换道经济车速优化示意图

2 车辆相关模型的建立

2.1 换道轨迹模型

在现有研究中，常见的车辆换道轨迹模型有等速偏移换道模型、圆弧轨道模型、基于期望侧向加速度换道模型和正弦函数换道模型。通常换道轨迹要满足两个条件:一是要保证换道轨迹曲率连续变化，没有突变；二是要保证换道轨迹始点和终点处曲率值为零，且便于转向驾驶操作。前两种模型形式简单但不满足换道轨迹曲率连续变化的要求，后两种模型曲线平滑性较好，但分别存在着操作不便和换道始末车轮转角不为零等问题。从简单实用的角度，结合等速偏移换道模型和正弦函数换道模型的优点，本文中采用 X-Sin函数模型，换道轨迹函数[10]为

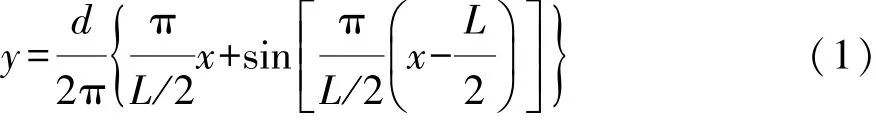
式中:d为两车道的中心线距离，d＝3.75m；L为完成换道过程沿车道方向的纵向位移。

对纵向位移变量x求导得

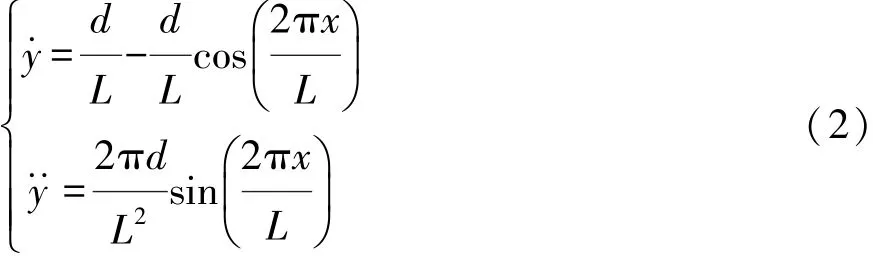
根据曲率计算公式，该换道轨迹上任一点的曲率K为

则当换道纵向距离长度L＝50m时，换道轨迹及其相应的曲率变化如图2所示。

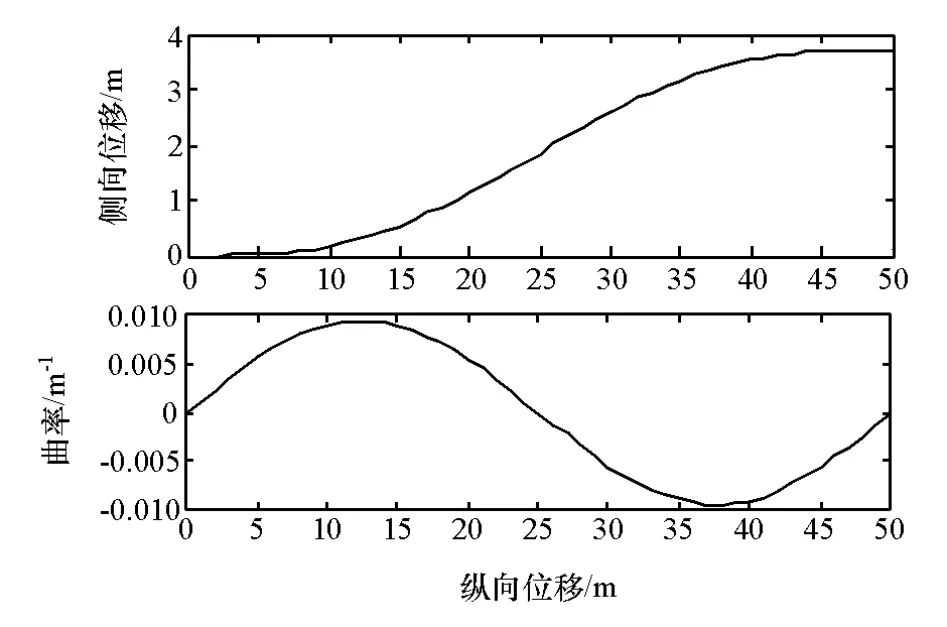
图2 换道轨迹及其相应的曲率变化示意图

由图2可知，基于X-Sin换道轨迹模型道路曲率连续变化，没有突变，且保证车辆在换道初始时刻和终了时刻的前轮转角为零，符合实际驾驶场景操作，且计算较为简单，因此该换道模型完全适用于换道经济车速的研究。

2.2 瞬态燃油消耗模型

现有经典的燃油消耗模型大多为稳态油耗模型，往往测量精度较差；而少数为瞬态燃油消耗模型，它通过引入瞬态变量来提高测量精度。基于本课题组研究基础，本文中采用基于“稳态初估＋瞬态修正”两模块组成的BIT-TFCM瞬态燃油消耗模型[11]。该模型稳态模块的输入为发动机转矩和转速，利用二维插值得到稳态油耗；模型瞬态修正模块为车辆速度和加速度，利用多项式拟合得到瞬态油耗和稳态油耗之间的差值。

瞬态燃油消耗的数学模型为

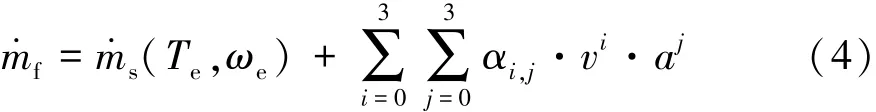
式中:s(Te，ωe)为稳态模块燃油消耗率；f为车辆瞬时燃油消耗率；Te和ωe分别为发动机转矩和角速度；αi，j为模型回归系数；v和a分别为车辆的瞬时速度和加速度。该部分所建油耗模型的数据来自于D3数据库[12]，选取了一款2013款现代索纳塔轿车测试数据来建模。

对建立的BIT-TFCM燃油消耗模型，进行了多种工况下的仿真验证，由于篇幅有限，图3仅示出在US06循环工况下的验证结果。由图可见，BIT-TFCM油耗模型估计的油耗值与实际油耗值较为吻合，表明所建油耗模型具有较高精度。

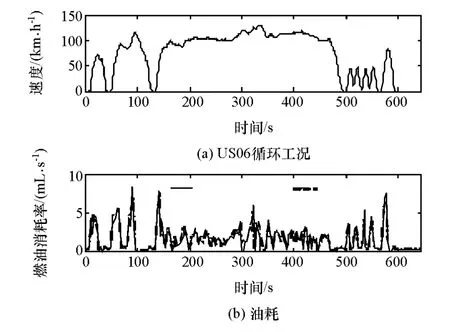
图3 US06循环工况仿真对比图

2.3 车辆动力学模型

因燃油经济性通常只考虑车辆在纵向的加速和制动情况，故建立纵向动力学模型。当车辆挡位固定时，有

式中:Ie为发动机转动惯量；Te为发动机输出转矩；Tc为离合器输入转矩。

若轮胎的转动惯量总和为Iw，车轮半径为rw，前轮牵引力为Fw，总传动比为i，传动系统效率为η，则存在如下关系:

接下来对车辆纵向受力进行分析，根据牛顿第二定律，车辆纵向动力学方程[13]为

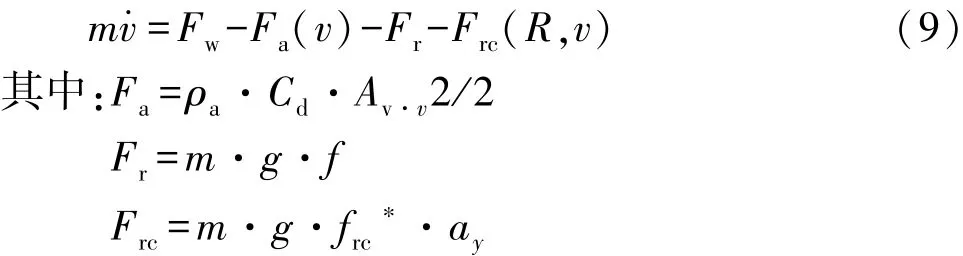
式中:Fa为空气阻力；ρa为空气密度；Cd为空气阻力系数；Av为迎风面积；Fr为不考虑侧偏时就存在的滚动阻力；f为滚动阻力系数；Frc为弯道行驶时附加的滚动阻力；frc为线性化的弯道滚动阻力系数斜率；R为弯道行驶时的车辆转弯半径。

考虑到轮胎有效的线性范围，图4给出了车辆弯道阻力系数frc与侧向加速度ay之间的关系。

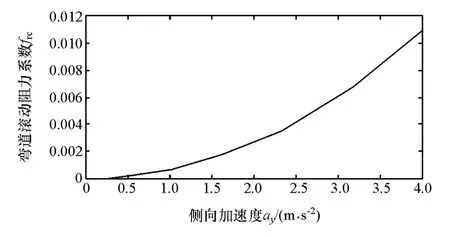
图4 frc与ay的关系(选用CarSim中215/55 R17轮胎)

由图4可见，当侧向加速度过大时，弯道滚动阻力系数会迅速增大，为方便分析问题，本文中只考虑轮胎线性工作范围，侧向加速度区间选取[0，2.5]m/s2，此时附加滚动阻力与侧向加速度成正比。综合式(5)～式(9)，可得

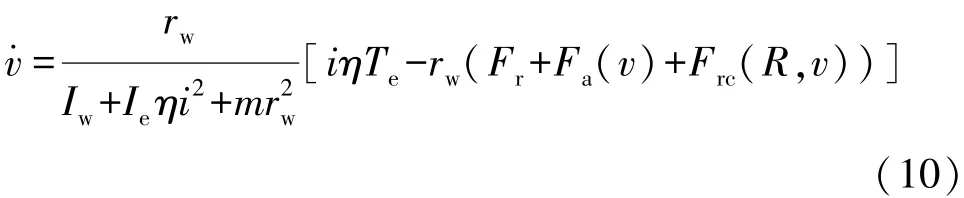
3 车辆经济车速推导

3.1 直道上稳态经济车速

相关研究表明，车辆在水平弯道上行驶时的稳态经济车速为定值[14]。为求直道上的稳态经济车速veco，可令车辆加速度v·＝0，同时Frc＝0，则由式(10)可得车辆在直道上作匀速行驶时的发动机转矩表达式为

此外，发动机转速ne和车速v之间的关系为

当车速和挡位已知时，便可得到相应的发动机转速和转矩。此时，便可作为油耗模型的一组输入得到相应的单位行程燃油消耗。通过计算不同挡位不同车速下的汽车单位行程燃油消耗，取其最小值便可得到对应的直道上的经济车速，结果如图5所示。由图可见，(56，0.05155)为整个图像的最低点，表明6挡时的56km/h是该车在直道上的稳态经济车速，即 veco＝56km/h。

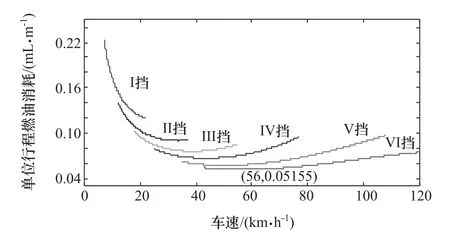
图5 不同挡位不同车速下单位行程燃油消耗

3.2 换道经济车速算法构建

换道经济车速问题可利用动态规划算法来解决。动态规划是基于Bellman最优化原理，适用于求解多段最优决策问题[15]。本文中研究问题的本质为一个确定性多阶段决策问题，因此采用离散系统的动态规划(dynamic programming，DP)算法来求解。

将式(10)按空间离散，得到系统状态方程为

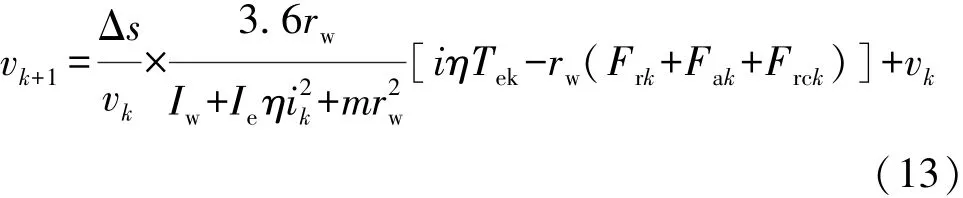
以车辆换道过程中的总燃油消耗作为系统代价，则车辆通过一段路程的代价函数为

由于车辆换道的初始和终点位置都在直道上，故车辆的始末状态都为直道上的稳态经济车速，即

将道路曲率作为扰动引入到系统中，则任意阶段k的道路曲率可根据式(3)离散化得到，即

考虑到车辆实际运动状态，须分别对车速、纵向加速度、侧向加速度和发动机转矩进行约束，即

4 实验结果与分析

下面将给出车辆在不同纵向换道长度下的换道经济车速仿真结果。对照仿真车辆选取CarSim中一款D级轿车，以直道上的稳态经济车速进行定速巡航(CC)模式行驶。仿真车辆相关模块参数与所建油耗模型车辆保持一致。换道轨迹路线可在Car-Sim中设置好，车辆可按照预期道路轨迹行驶，且由PI控制器来调节车辆的制动与油门，以跟随设定的定速巡航车速。

出于安全角度考虑，换道纵向长度不可太短，故下面考虑L＝50m和L＝80m下仿真结果，如图6和图7所示，其中DP表示动态规划算法给出的实验结果，CC表示定速巡航算法给出的实验结果。

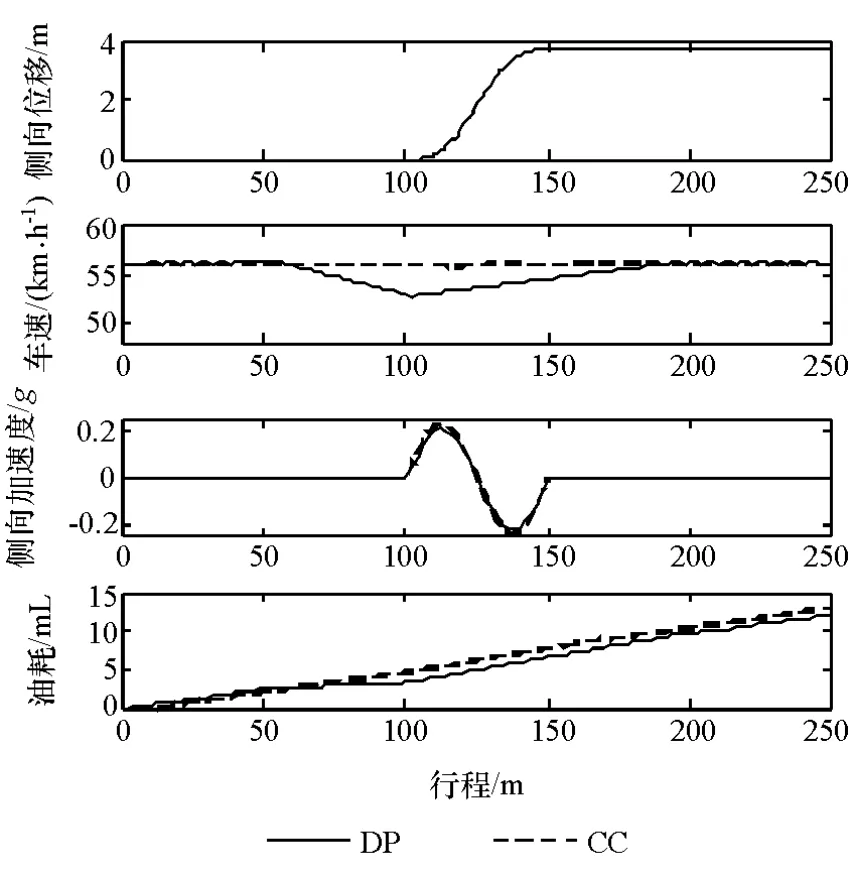
图6 L＝50m换道车速仿真结果

由图6可见，当L＝50m时，采用定速巡航算法消耗燃油 13.01mL，而采用 DP算法消耗燃油11.94mL，DP算法节油达8.22%。由图7可见，当L＝80m时，采用定速巡航算法消耗燃油14.46mL，DP算法耗油13.31mL，DP算法节油效果为7.95%。从经济车速曲线(图6(b)和图7(b))来看，车辆在进入换道之前首先有一小段轻微的加速过程，在此之后有一段明显的减速过程；在开始换道操作时便逐渐加速，直到加速至直道上的稳态经济车速。另外，从侧向加速度图中(图6(c)和图7(c))可以看出，车辆的侧向加速度较小，保证车辆轮胎处在线性区间。

图7 L＝80m换道车速仿真结果

此外，通过大量实验可以发现，随着换道纵向长度L逐渐增大，车辆进入换道前下降的车速差逐渐减小，当L＞250m以后，DP规划出的车速与CC车速基本重合，这说明当换道纵向长度足够大时，车辆保持直道上的经济车速行驶即可实现该过程燃油经济性最大化。究其原因，主要是因为随着换道纵向长度的增加，换道轨迹道路曲率变化绝对值越来越小，直至趋近于零。从本质上来说，是因为在换道轨迹曲率值较大处由轮胎侧偏现象引起的附加滚动阻力明显增加，从而影响车辆在换道时的经济车速。

5 结论

本文中提出了基于车辆换道轨迹道路曲率信息的经济车速优化方法。车辆通常在直道上保持稳态经济车速行驶即可，当需要执行换道操作时，根据提前规划好的换道轨迹，利用动态规划算法可得换道时的经济车速轨迹，在保证换道安全、舒适的前提下实现换道总过程燃油经济性最大化。通过CarSim与Matlab/Simulink联合仿真，验证了换道经济车速优化算法的有效性。当换道纵向长度逐渐增大时，换道经济车速曲线逐渐平缓，即与直道经济车速趋于一致。这是因为随着换道纵向长度逐渐增大，换道轨迹道路曲率变化逐渐减小，由轮胎侧偏现象引起的附加滚动阻力也逐渐减小，直至为零。该技术可在智能车辆安全行驶的基础上，提升其燃油经济性，为智能车辆换道时的速度控制提供决策依据。

[1] 陈慧岩.无人驾驶汽车概论[M].北京:北京理工大学出版社，2014.

[2] 上汽集团“新能源＋互联网＋X”亮相上海车展[EB/OL].http://www.cs.com.cn/ssgs/gsxw/201504/t20150420＿4691176.html，2015－04－20.

[3] SMITH B W.Summary of levels of driving automation for on-road vehicles[J].Center for Internet and Society， Stanford Law School，2013.

[4] 国务院.国务院关于印发《中国制造2025》的通知[EB/OL].http://www.gov.cn/zhengce/content/2015－05/19/content＿9784.htm，2005－05－08/2005－05－19.

[5] MARSDEN G，MCDONALD M，BRACKSTONE M.Towards an understanding of adaptive cruise control[J].Transportation Research，2001，9(1):3－51.

[6] BOSE A，IOANNOU P A.Analysis of traffic flow with mixed manual and semi automated vehicles[J].IEEE Transactions on Intelligent Transportation Systems，2003，4(4):173－188.

[7] SHIDA M，DOI T，NEMOTO Y，et al.A short-distance vehicle platooning system 2nd report-evaluation of fuel savings by the developed cooperative control[C].Proceedings of the 10th International Symposium on Advanced Vehicle Control(AVEC)，2010，Lough borough，UK.

[8] WU C X，ZHAO G Z，OU B.A fuel economy optimization system with applications in vehicles with human drivers and autonomous vehicles[J].Transportation Research Part D，2011，16(7):515－524.

[9] RAHMAN M，CHOWDHURY M，XIE Y，et al.Review of microscopic lane-changing models and future research opportunities[J].IEEE transactions on intelligent transportation systems，2013，14(4):1942－1956.

[10] ZHANG S，LIUW，LIB，et al.Trajectory planning of overtaking for intelligent vehicle based on X-Sin function[C].Mechatronics and Automation(ICMA)，2014 IEEE International Conference on.IEEE，2014:618－622.

[11] ZHOU M，JIN H.Development of a transient fuel consumption model[J].Transportation Research Part D:Transport and Environment，2017，51:82－93.

[12] Argonne National Library， Transportation Technology R＆D Center.Downloadable dynamometer database[DB].http://www.transportation.anl.gov/D3/.

[13] SCHWICKART T，VOOSH，HADJI-MINAGLOU J R，et al.A fast model-predictive speed controller for minimised charge consumption of electric vehicles[J].Asian Journal of Control，2016，18(1):133－149.

[14] FRÖBERG A， HELLSTRÖM E， NIELSEN L.Explicit fuel optimal speed profiles for heavy trucks on a set of topographic road profiles[C].SAE Paper 2006－01－1071.

[15] BELLMAN R.Dynamic programming[M].Princeton University Press，1957.