商用车鼓式制动器热流双向耦合分析技术研究

陈 静，张 群，陈 莹，韩业鹏，刘艳贺，韩忠田

(1.中国一汽解放商用车开发院，长春 130011； 2.英特工程仿真技术(大连)有限公司，大连 116023)

前言

鼓式制动器在客车和重型车辆上具有广泛的应用，它的温度场分析对于摩擦制动器的制动性能乃至汽车行驶安全性和可靠性尤为关键[1]。随着汽车行业技术水平的提高，汽车不断地向高速、重载的方向发展，在此条件下的频繁或长时间制动，对汽车制动鼓的使用寿命提出了新的挑战。深入研究鼓式制动器在制动过程中的温度状态，分析其影响因素，完善研究方法，对于设计开发出具有足够热容量、在高温条件下保持足够机械强度的制动鼓结构，具有重大的理论与现实意义。

鼓式制动器工作过程中产生的热量主要通过导热和对流的方式进行传递和交换，对制动器生热和能量交换过程的研究涉及摩擦学、流体力学、接触力学和传热学等，是一个典型的热流耦合问题。目前国内外对该类问题的分析通常采用热流顺序耦合的方法[2－6]，即先进行制动器与工作环境的流场仿真分析，输出制动鼓在恒转速和恒温条件下与外界空气的对流换热系数，然后将获得的对流换热系数作为边界条件加载到传热模型中。热流顺序耦合方法虽然计算效率较高，但并未考虑环境温度升高对对流换热系数的影响，根据文献[7]中关于对流换热系数对制动器散热效果的研究可知，随着制动次数的增加，对流换热系数对制动器散热效果的影响将不可忽视，因此，热流顺序耦合方法不适用于多次制动工况。文献[8]中利用ANSYS Workbench平台针对盘式制动器建立了一种三维热流双向耦合分析模型，即流场和热场的数据交换是双向的，但由于盘式制动器与鼓式制动器在摩擦面上的压力分布形式不同，且该模型未考虑摩擦因数的非线性变化，所以不能完全应用到鼓式制动器上。

为建立一套适用于多次制动过程且能够准确描述接触属性的非线性变化、满足工程要求的鼓式制动器热流双向耦合分析方法，本文中开发了一套制动器专用热流双向耦合数值模拟方法。该方法充分利用了不同分析领域商用软件的优势，通过脚本语言控制Fluent和ABAQUS软件，分别进行制动器与周围环境的流场分析和制动器摩擦生热与传热分析。软件之间的数据传递、数据映射和插值以及收敛性判断等均通过编程语言实现，能够实现流体场和温度场数据的实时双向传递。为了验证所开发方法的精度，对鼓式制动器台架试验正常路面工况进行了热流双向耦合仿真，结果表明，该方法技术手段先进，分析精度高，能有效地帮助设计师提高制动器结构设计的可靠性。

1 热流双向耦合理论分析

1.1 摩擦生热分析

制动过程中，摩擦片与制动鼓的摩擦生热是鼓式制动器热流耦合仿真分析的热量来源，能否准确描述该行为是提高仿真精度的关键因素。假定消耗的机械能完全转化为热能，则制动过程中摩擦接触面上单位时间单位面积上产生的热量即热流密度可以表示为

式中:q为热流密度；f为摩擦因数；p为接触压强；v为制动鼓和摩擦片的相对速度。摩擦热流平均分配到制动鼓和摩擦片上。

古典滑动摩擦理论认为两物体表面的摩擦因数只与材料属性有关，与摩擦接触面积、相对运动速度和正压力无关。然而在实际工程计算和调研相关文献[9－10]后发现，实际的摩擦因数也会因相对滑动速度、制动器温度和压强的波动而改变。根据试验结果拟合获得的制动鼓摩擦因数随制动压强p、车速v和接触点温度T变化的关系为

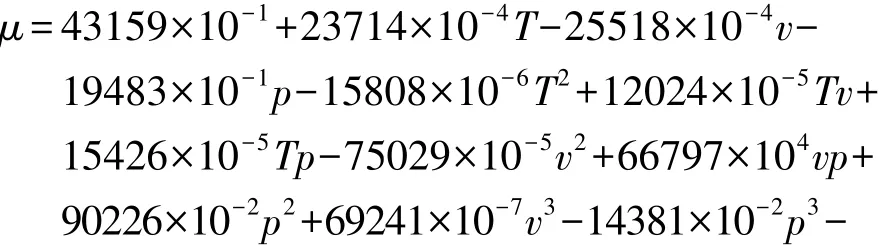
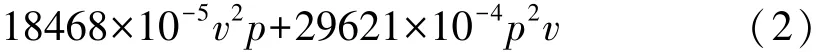
本文中利用ABAQUS软件的用户子程序二次开发功能，应用Fortran语言定义并在计算过程中实时读取制动鼓摩擦面各节点的空间位置，根据节点不同空间位置的线速度、压强、温度值按式(2)计算得到该点的摩擦因数，进而通过式(1)得到该点的热流密度值。

1.2 传热学分析

在热力学分析中，热量的传递方式包括:热传导、热对流和热辐射3种。鼓式制动器系统内进行热量传递的方式主要是热传导，与周围空气介质进行热量交换的方式是热对流和热辐射。鼓式制动器系统通过热辐射与周围空气交换的热量约占总换热量的5%～10%[11]，本文中将热辐射损失系数定为0.05，该系数将直接作用到式(1)热流密度值的计算中。

在不考虑热辐射的基础上，鼓式制动器系统与周围空气介质相接触的自由表面满足牛顿冷却定律:

式中:h为对流换热系数，与流体的速度、接触面的形状和温差密切相关；T为制动鼓与周围空气的接触面温度；T0为周围空气温度。

1.3 流体分析

制动鼓周围流场的相对速度远低于0.3Ma，可视为不可压缩湍流运动。流体分析过程中遵循质量守恒定律、动量守恒定律和能量守恒定律。湍流模型采用标准k-ε方程，包括湍流动能方程和湍流应力方程，在忽略浮力项的影响的条件下，它们分别为

式中:k为湍流动能；ε为湍流动能耗散率；μ为动力黏性系数；μt为湍流黏度梯度引起的湍动能项；C1ε，C2ε，Cμ，σk和 σε为模型常数，取值分别为 1.44，1.92，0.09，1 和 1.3。

1.4 耦合分析

耦合方法可以分为强耦合(直接耦合)和弱耦合(迭代耦合)两种[12]，强耦合方法直接对统一的耦合方程进行求解，耦合方程中的变量将同时更新。与此相反，弱耦合方法对单场分别求解，物理场之间的耦合通过耦合面上的数据传递实现。本文中采用弱耦合的方法计算制动鼓热流双向耦合问题，对流体场和温度场采用单独的求解器，在热流耦合界面，需要满足温度的连续性条件和热流平衡条件:

式中:Tf为流体场界面温度；Ts为温度场界面温度；qf为流体场界面热流密度；qs为温度场界面热流密度。

耦合面间的数据映射和插值采用控制面法，此算法具有全局守恒的特点，能够保证最精确的数据映射和插值结果。流固耦合界面数据传递的收敛性判断公式为

其中 ε＝‖ϕnew－ϕpre‖/‖ϕnew‖

式中:ε为对耦合面传递的数据进行归一化处理的结果；ϕnew为当前耦合迭代步的耦合界面载荷矢量；ϕpre为上一个耦合迭代步的耦合界面载荷矢量；toler为用户输入的容差值。当ε∗≤0，即 ε＜toler时，默认收敛。

热流双向耦合分析的具体流程如下，流程示意图如图1所示。

(1)通过脚本控制启动Fluent软件开始流场分析，计算制动鼓初温条件下的表面热流量，计算完成后输出耦合面上的热流量值，将输出的热流量作为初始面载荷，通过点对点的映射和插值加载到ABAQUS热场分析模型中。

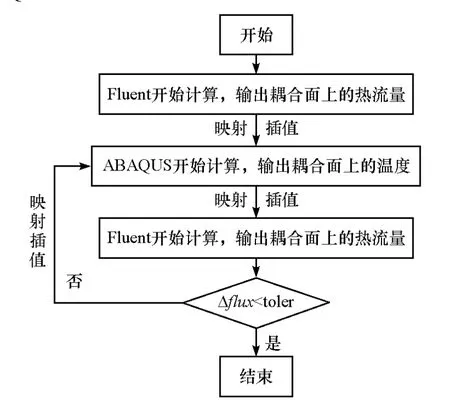
图1 鼓式制动器热流双向耦合分析控制流程

(2)通过脚本控制启动ABAQUS软件进行热场分析，计算完成后输出耦合面上的温度值，将输出的温度值作为壁面边界条件，通过点对点的映射和插值加载到Fluent流场分析模型中。

(3)重复Fluent软件与ABAQUS软件之间的数据传递，当热流量值的计算残差小于用户输入的容差值时，耦合平衡，计算结束。

图中，Δflux相当于式(8)中的 ε，Δflux＝‖fluxnew－fluxpre‖/‖fluxnew‖，表示耦合界面上热流量变化的归一化值。

2 热流双向耦合验证算例

2.1 模型描述

鼓式制动器热流双向耦合分析基于台架试验工况进行，包括热场分析模型和流体场分析模型两部分。采用ABAQUS的热-结构位移耦合模块对制动鼓进行热场分析，热场分析模型包括制动鼓和摩擦片。为提高计算精度和效率，对制动鼓和摩擦片采用规则六面体网格，整体网格数量约为4万，如图2所示。制动鼓与摩擦片表面定义接触关系，在摩擦片上各节点通过用户子程序施加热流载荷。制动鼓绕轴向转动，摩擦片固定不动。制动鼓材料为灰铸铁，摩擦片为非石棉基复合材料，在ABAQUS中分别定义这两种材料随温度变化的弹性模量、泊松比、密度、热膨胀系数、热导率和比热容。

图2 鼓式制动器热分析模型

流场分析模型以整个制动器惯性试验台箱体空间为基础，包括:惯性试验台箱体、气体进出口、鼓式制动器总成、配重、密封盖和台架，如图3所示。采用滑移网格模拟制动鼓及配重的旋转运动，滑移面之内为内部旋转域，滑移面之外为外部域，制动鼓及配重表面边界层采用棱柱单元，第一层厚度为0.1mm，共8层单元，内部域与外部域全部采用四面体网格，整个流体场模型网格数量约为11.5万，整体模型剖面如图4所示。

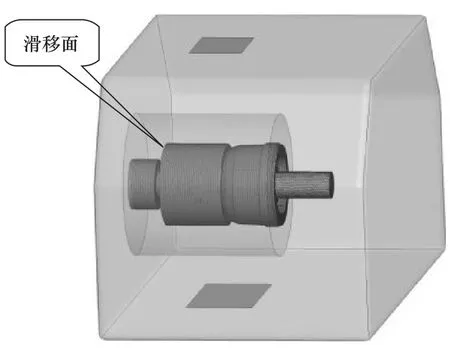
图3 鼓式制动器流场分析模型

图4 鼓式制动器流场模型剖面图

2.2 工况描述

鼓式制动器热流双向耦合分析以制动器企业标准台架试验工况作为验证算例，初始车速为50km/h，匀减速制动4.63s，制动末速度为0，平均制动力矩为11 700N·m，然后解除制动加速回50km/h，散热55.37s，之后再次重复以上工况，总共反复20次制动-散热循环，制动鼓初温为80℃，试验台进口风速为3m/s，进口温度为15℃。

2.3 分析结果

查看制动鼓热流耦合面瞬时表面换热系数分布情况，如图5所示。由图可见，制动鼓表面不同位置的换热系数均不相同。制动-散热周期60s内制动鼓热流耦合面换热系数最大值的时域变化曲线如图6所示。由图可见，制动初期由于制动鼓温升较快，与环境温差大，换热系数持续上升，进入散热阶段后，随着制动鼓与环境温差的逐渐减小，换热系数变化率逐渐减小，趋于稳定。由以上分析结果可见，该制动器热流双向耦合分析方法既考虑了制动鼓表面不同位置的换热差异性，又考虑了换热的时域差异性。

分别提取制动鼓内外壁面测温点在每个循环周期(20次)制动结束时刻和散热结束时刻的温度值，绘制成的温度随制动周期的变化曲线如图7所示，其中横坐标中的刻度1代表第1个周期制动结束时刻，2表示第1个周期散热结束时刻，3表示第2个周期制动结束时刻，以此类推。由图可见，制动鼓内外表面温度呈波浪形上升趋势，每个周期制动结束时刻温度最高，散热结束时刻温度最低，这种温度周期性的升高降低，将最终导致制动鼓出现热疲劳现象。在20次循环制动散热过程结束后，制动鼓内表面温度从最开始的80升高至239.3℃。制动鼓外表面温度从最开始的80升高到208℃。

图5 制动鼓实时表面换热系数分布云图

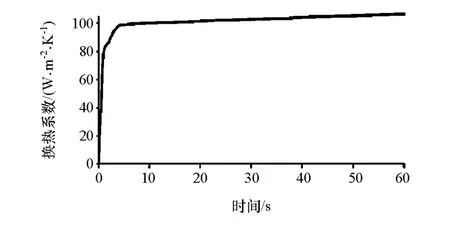
图6 制动鼓表面最大换热系数时域变化曲线

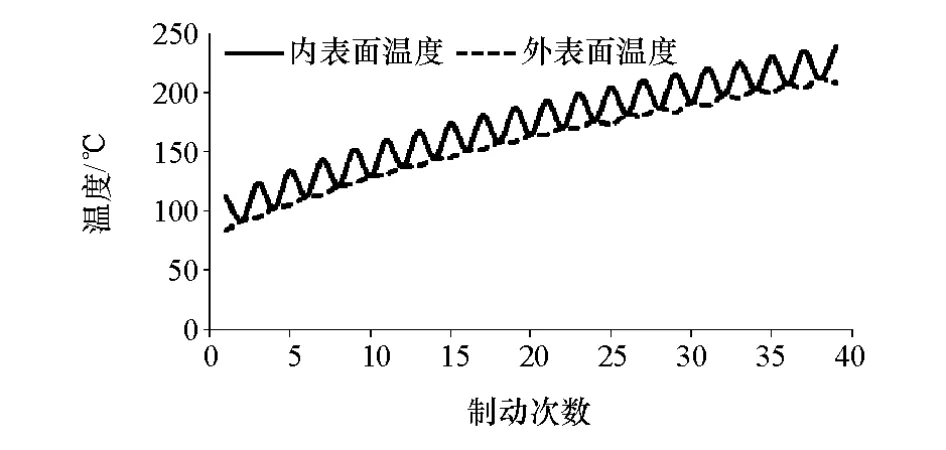
图7 20次连续制动工况制动鼓内外表面温度变化曲线

图8 为第20个循环周期，制动鼓制动结束时刻径向和轴向温度分布，此时制动鼓的温度在径向和轴向上均存在温度梯度，最高温度达到239.3℃。为了防止摩擦副在高温下出现晶相组织变化，进而导致在连续下坡路段，频繁制动时发生制动失效[7]的问题，设计时可将制动鼓内最高温度作为设计指标，控制摩擦副间的最高温度在300℃以下。散热结束后制动鼓整体温度分布如图9所示，此时制动鼓内外表面径向温度分布基本趋于一致，而轴向温度在连接法兰处仍存在温差。

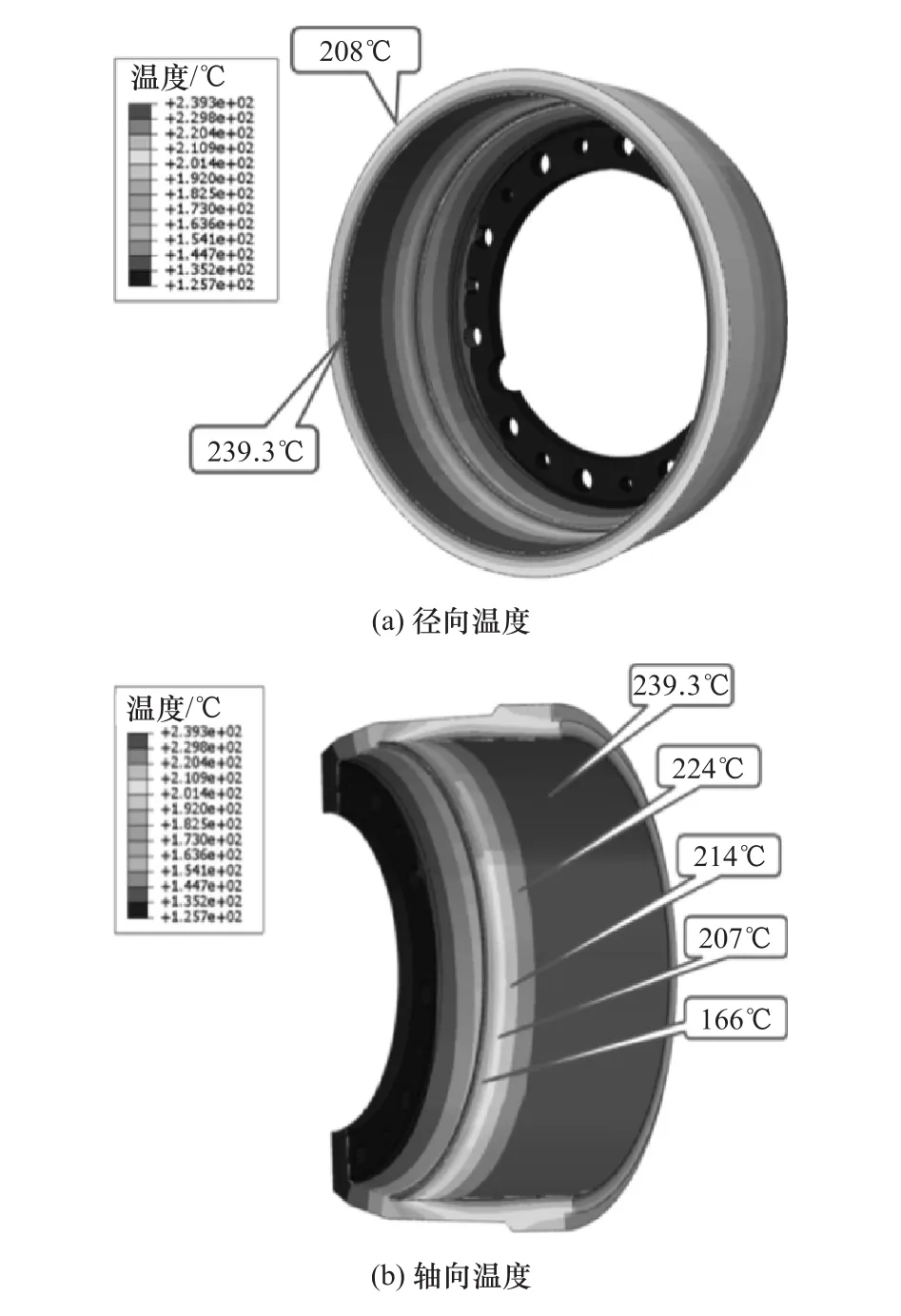
图8 制动鼓制动结束后径向和轴向温度分布

图9 散热结束时制动鼓温度分布

3 制动鼓热流双向耦合分析精度

3.1 制动鼓正常路面工况台架试验

制动鼓正常路面工况台架试验在重型汽车制动器惯性试验台上进行，整体台架如图10(a)所示，为减小试验测试数据的离散性，提高精度，试验采用3件制动鼓总成样品。使用高精度耐高温热电偶，在距制动鼓外表面端口15cm处，从外表面向内打一穿透的小孔，将热电偶从内孔塞入，打磨平整，与制动鼓内表面完全齐平，共埋放2个热电偶，位置相对，如图10(b)所示。热电偶引线统一安装在集流器上。试验前应注意检测制动鼓整体圆周跳动量，试验环境同仿真分析条件完全相同，试验中实时监控3个样品各2个测点的温度值。

图10 制动鼓试验现场和热电偶埋放位置

3.2 精度对比

3个试验样品测温点1和测温点2的试验温升曲线如图11和图12所示，为消除试验误差，分别对测温点1和测温点2的3个样品取均值，作为试验对比结果。同时，因为测温点1和测温点2是制动鼓同一个圆周上相对180°的两个点，无法与仿真模型中同一圆周上的具体点定位，又因为制动鼓同一圆周上各位置温度基本一致，所以将距制动鼓外表面端口15cm处圆周上所有节点的仿真温度取平均值，作为仿真对比结果。试验对比结果和仿真对比结果随制动周期的变化曲线如图13所示。

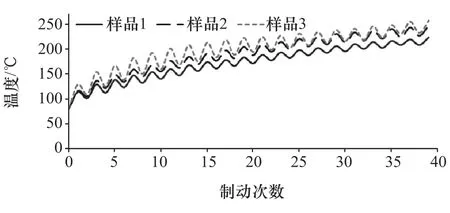
图11 3个样品测温点1试验温升曲线

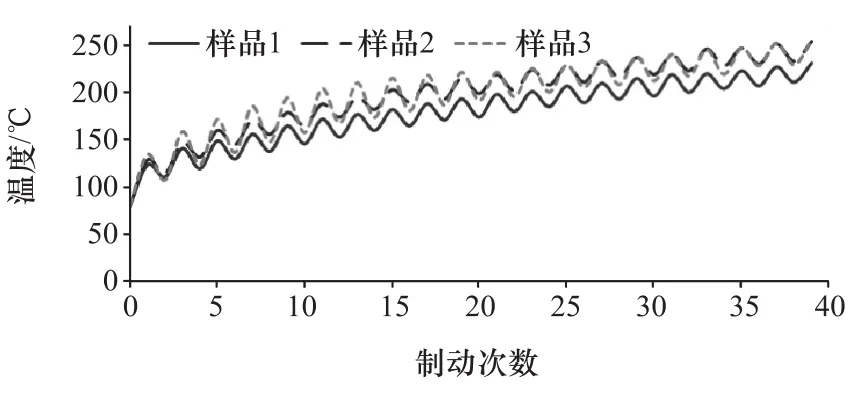
图12 3个样品测温点2试验温升曲线

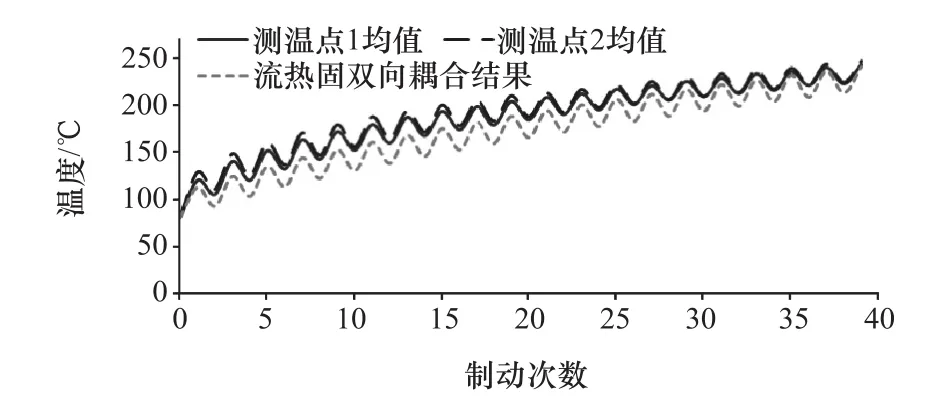
图13 仿真均值与试验测点1均值、试验测点2均值随制动周期变化曲线

采用试验值与仿真值的相对误差对数据进行误差分析。仿真温度值与测温点1和测温点2温度值的相对误差随制动周期的变化曲线如图14所示。

图14 仿真均值与试验测温点1均值、试验测温点2均值随制动周期变化的相对误差曲线

由图可见:仿真值与试验值的误差随着循环次数的增加逐渐减少；在20次循环制动散热过程中，仿真温度值与测温点1温度值的最小相对误差仅为1.2%，最大相对误差约为14%；仿真温度值与测温点2温度值的最小相对误差仅为2.7%，最大相对误差约为17%，整体精度在83%以上。

4 结论

本文中开发的制动器热流双向耦合分析方法，既实现了在分析中引用摩擦副摩擦因数按节点空间位置随压强、温度和速度实时变化结果的能力，又实现了自动控制Fluent软件和ABAQUS软件之间的热流耦合分析的功能，与常规的热流顺序耦合方法相比，考虑问题全面，能准确还原模拟制动器的实际工作状态，特别适用于汽车多次循环制动散热问题。通过与台架试验的精度对比，开发的制动器热流双向耦合分析方法整体精度在83%以上，能够满足工程要求，该方法具备工程应用推广价值。

[1] 包圳，苏小平，张桃沙.汽车鼓式制动器热结构耦合分析与仿真[J].机械设计与制造，2015(8):189－192.

[2] 赵凯辉，魏朗.鼓式制动器三维热 机耦合温度场仿真[J].农业机械学报，2009(2):32－36.

[3] 张立军，陈远，刁坤，等.盘式制动器接触压力与热机耦合特性仿真分析[J].同济大学学报:自然科学版，2013，41(10):1554－1561.

[4] 包圳，苏小平，张桃沙.汽车鼓式制动器热结构耦合分析与仿真[J].机械设计与制造，2015(8):189－192.

[5] VOLLER G P，TIROVIC M，MORRISR，et al.Analysis of automotive disc brake cooling characteristics[J].Proceedings of the Institution of Mechanical Engineers，Part D:Journal of Automobile Engineering，2003，217(8):657－666.

[6] BELHOCINE A，BOUCHETARA M.Thermal analysis of a solid brake disc[J].Applied Thermal Engineering，2012，32:59－67.

[7] ADAMOWICZ A，GRZES P.Influence of convective cooling on a disc brake temperature distribution during repetitive braking[J].Applied Thermal Engineering，2011，31(14):2177－2185.

[8] 曾红，苏国营，郭超，等.盘式制动器流固耦合传热仿真分析及试验研究[J].机械传动，2016(9):114－117.

[9] 王成焘，姚振强，陈铭.汽车摩擦学[M].上海:上海交通大学出版社，2002.

[10] 陈兴旺.鼓式制动器制动温度场的研究[D].西安:长安大学，2006.

[11] 陈晋兵.重型载货车辆鼓式制动器热力耦合有限元分析[D].太原:太原理工大学，2011.