汽车乘员约束系统多目标不确定性优化∗

刘 鑫，付 庆，尹来容，张志勇

(1.长沙理工大学，工程车辆安全性设计与可靠性技术湖南省重点实验室，长沙 410114；2.长安大学，汽车运输安全保障技术交通行业重点实验室，西安 710064)

前言

当汽车发生碰撞时，由安全带、安全座椅和安全气囊等装置组成的乘员约束系统不但能有效缓冲乘员所受到的冲击载荷，还能避免乘员与车身内饰发生二次碰撞，从而起到汽车乘员防护作用。研究表明[1－2]，汽车乘员约束系统的防护性能将直接决定乘员的损伤程度和死亡率。因此，汽车乘员约束系统是汽车安全技术研究的重中之重。

然而，目前对于汽车乘员约束系统的研究，多数是在系统参数模型处于确定性条件下展开讨论的[3－4]。但在实际的汽车碰撞过程中，由于路况条件、边界条件和初始条件存在误差或不确定性，如果仍把这些因素看作确定性因素来对待，则将导致系统响应与实际响应产生较大的偏差。同时，在汽车碰撞过程中的很多问题通常由相互冲突的多个目标组成。特别是对乘员约束系统进行设计时，既要考虑能最大限度地保护乘员头部，又要考虑使其胸部损伤值最小，同时还要考虑乘员的腿部损伤值不能超过人体的耐受极限，这些设计目标的改善可能相互抵触。而且，对于乘员约束系统这类复杂的工程多目标优化问题而言，往往涉及非常耗时的数值分析模型。因此，为提高优化效率，基于近似模型技术的优化方法得到了广泛应用[5－6]，该方法主要是通过构造简单的显式函数作为近似模型来替代原数值分析模型，并与非线性优化技术相结合以构造近似优化问题进行快速计算。

据此，本文中基于局部加密近似模型技术，研究针对汽车乘员约束系统的多目标不确定性优化设计方法。首先基于MADYMO分析软件建立某型汽车前碰撞乘员约束系统数值模型，并通过开展实车前碰撞试验对该模型进行校正；然后通过区间变量来描述乘员约束系统不确定性参数的波动范围，并利用区间序关系将不确定性优化问题转换为确定性优化问题；为提升计算效率和计算结果的精度，将局部加密近似模型技术引入迭代求解过程，并通过多目标不确定性优化方法求解满足乘员约束系统防护性能的非支配解集(Pareto最优解集)，从而确保汽车乘员的安全性。

1 乘员约束系统数值模型的建立与验证

1.1 模型的建立

针对某微型客车100%正面碰撞工况，并结合MADYMO分析软件建立了乘员约束系统数值模型，如图1所示。该模型主要由车体、假人和安全带3大部分组成。其中，车体模型主要采用多刚体模型进行构建，包括地板、座椅、转向系统、前围板、脚踏板、A柱和前风窗玻璃；假人模型采用HybridⅢ 50百分位多刚体男性假人；安全带模型则采用混合三点式安全带模型，包括织带、带扣、D－环和锚点。整个碰撞过程由MADYMO多刚体动力学软件进行仿真求解，从而获得假人头、胸、腿各部位的动态响应曲线和损伤指标值。

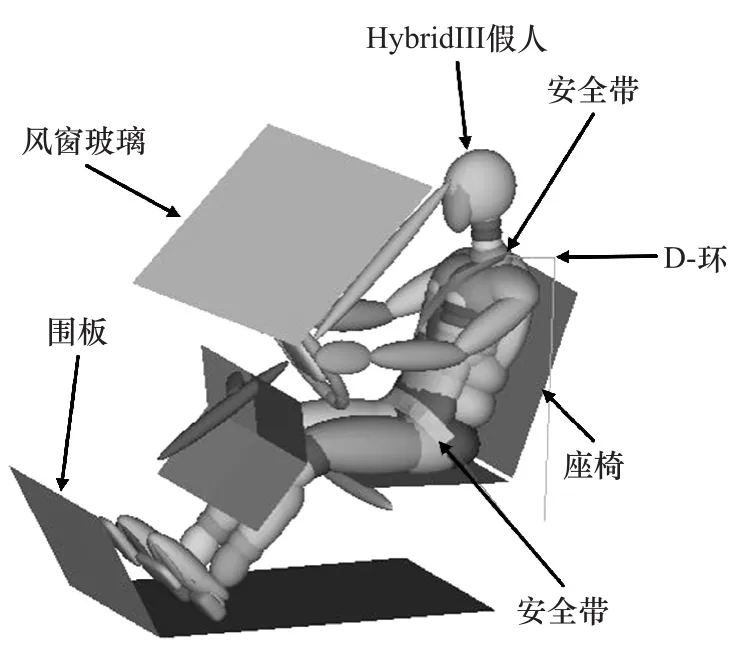
图1 乘员约束系统数值模型

1.2 试验验证

为验证上述汽车乘员约束系统数值模型的准确性，本文按照GB11551—2003《乘用车正面碰撞的乘员保护》所规定的试验方法和程序进行了实车碰撞试验。

首先通过NI数据采集系统获得车体所受的冲击加速度曲线(图2)和假人头、胸、腿部的动态响应曲线(图3)。然后将实车碰撞试验获得的车体所受冲击加速度曲线作为数值模型的输入，通过数值仿真计算亦可获得假人头、胸、腿部的动态响应曲线，并将仿真结果与试验结果进行对比来不断校正数值模型的准确性，直到满足要求为止。

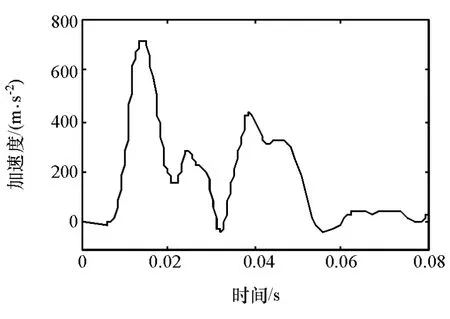
图2 车体所受的冲击加速度曲线

图3 为假人动态响应曲线仿真与试验结果对比，图4为假人运动响应仿真与试验结果对比，表1为假人损伤响应仿真与试验结果对比。从图3和表1可以看出，右大腿轴向压力FFR的仿真数据与试验数据存在差异，这是由于在汽车碰撞试验过程中，乘员座椅与车身之间的链接部件发生变形，致使试验假人体位发生偏转，因此导致右大腿轴向压力FFR产生误差。总体来说，假人头部、胸部和腿部动态响应曲线的仿真与试验结果基本吻合，虽存在一定的误差，但各响应曲线的峰值误差均在10%以内，且峰值出现的时间基本一致，且图4中的假人运动响应仿真图像与试验结果相对一致，说明该数值模型和建模方法是有效的，可在此模型上进行优化设计。

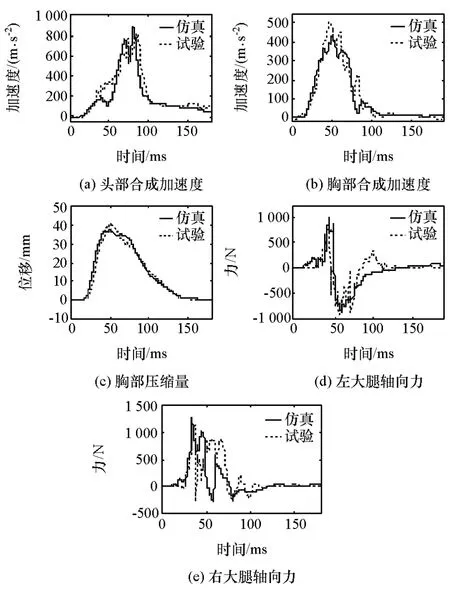
图3 假人动态响应曲线仿真与试验结果对比

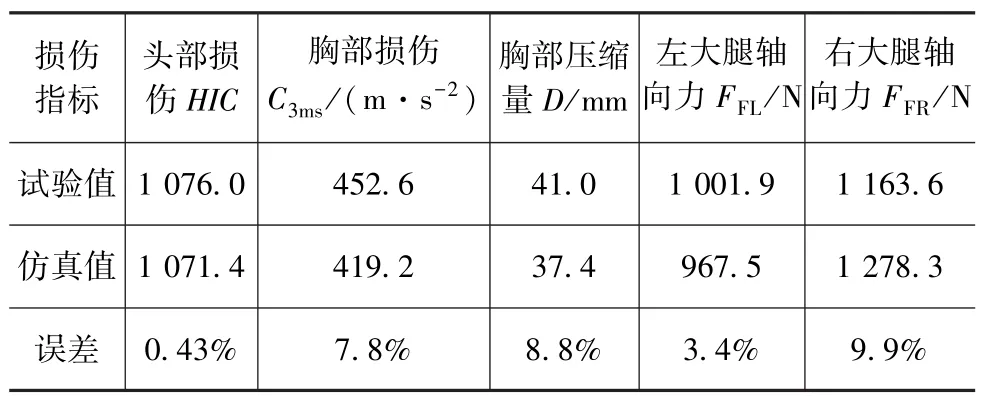
表1 假人损伤响应仿真和试验结果对比

2 乘员约束系统不确定性优化问题的描述

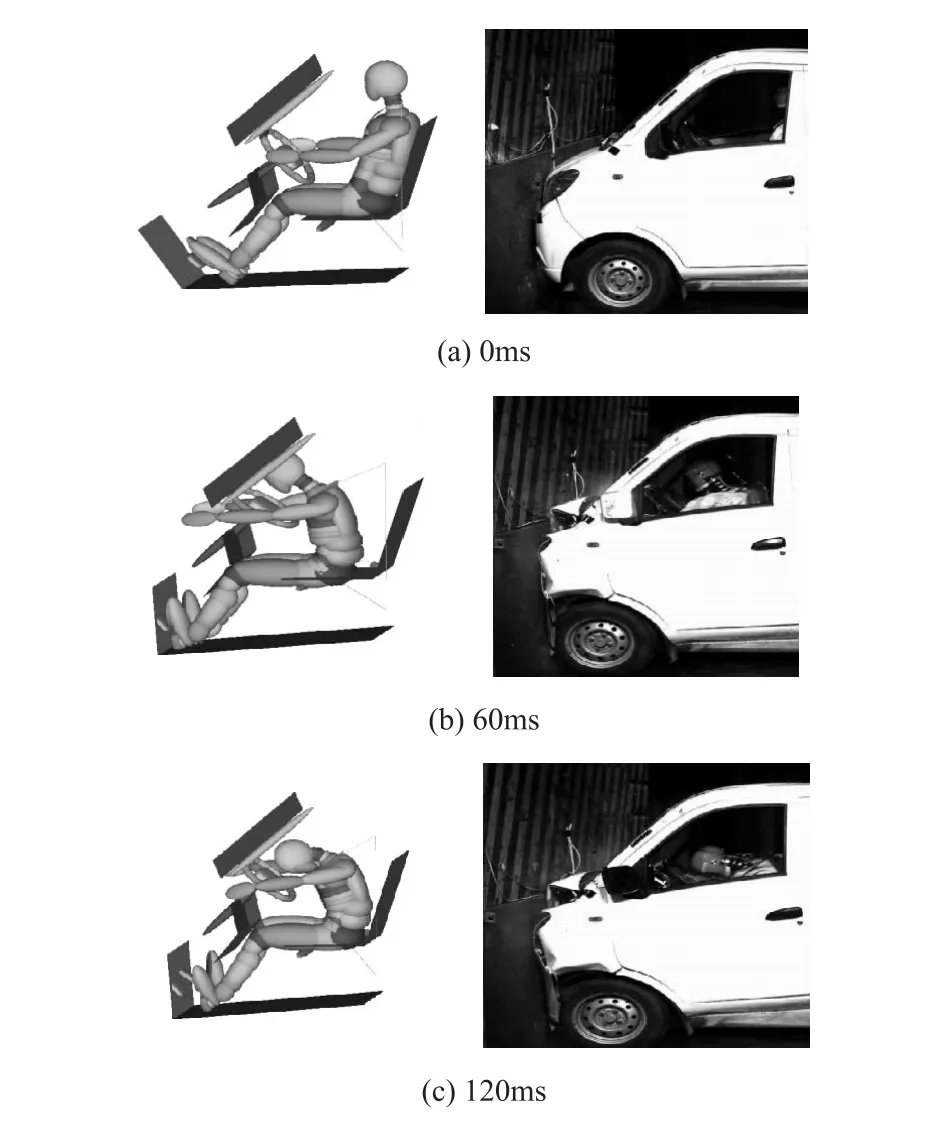
图4 假人运动响应仿真与试验结果对比

从表1可知，目前乘员约束系统对人体头部和胸部的防护效果较差，其中头部损伤 HIC值为1 076，超过了国家标准GB11551—2003规定的极限值1 000；胸部损伤C3ms加速度值为452.6m/s2，也接近人体的耐受极限值600m/s2。而人体的大腿轴向力值远小于人体的耐受极限10 000N，说明该乘员约束系统对腿部具有较好的防护效果，因此选取头部综合性能指标HIC值和胸部C3ms加速度值作为优化目标，胸部压缩量D和左、右大腿轴向压力FFL，FFR作为约束条件；在设计过程中，乘员约束系统可通过调整安全带上挂点的位置、锚点的位置和安全带伸长率来完善其防护效能，因此选取以上3种变量作为设计变量；考虑到制造和安装的误差将导致安全带的初始应变和座椅的刚度存在一定的波动，所以把它们作为不确定性变量，则可建立不确定性优化设计模型如下:

式中:f1为头部损伤HIC值；f2为胸部损伤的C3ms值；g1为胸部压缩量D值；g2与g3分别为左、右大腿轴向压力FFL与FFR；X为设计变量，其中X1为安全带上挂点的位置，X2为安全带锚点位置，X3为安全带伸长率；U为不确定性变量，其中U1为安全带的初始应变，U2为座椅的刚度系数。由于式(1)所示的优化问题包含了不确定性向量U，所以导致传统的优化方法无法有效对其进行求解。下面将利用非线性区间数规划对上述不确定优化问题进行求解。

3 乘员约束系统特性参数不确定性优化

3.1 不确定目标的转换

区间序关系用于判断一区间是否优于或劣于另一区间，以用于区间数的排序[7]。本文中采用文献[7]区间序关系≤cw处理式(1)中的不确定目标函数。区间序关系≤cw为

式中:I为区间；c和w分别为区间的中点值和半径。

式(2)表示当BI的中点和半径均小于或等于AI的中点和半径时，则BI要优于或等于AI。用序关系≤cw比较式(1)中的目标函数，以期找到一个最优的设计向量，使头部损伤HIC值和胸部损伤C3ms值的区间具有最小的中点值和最小的半径，则式(1)中的乘员约束系统多目标中的每一个子目标函数可转换为如下的确定性多目标优化问题:

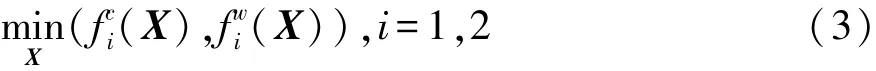
其中

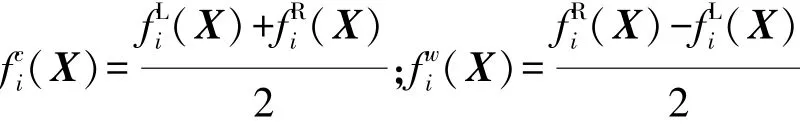
式中:分别为目标函数的区间中点和区间半径，L和R分别为区间下界和区间上界。对于任一设计向量X，目标函数fi的区间上下边界可通过下式求解:

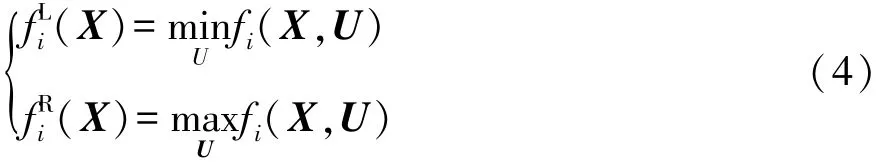
其中 U＝{U｜－0.05≤U1≤0，0.9≤U2≤1.0}

3.2 不确定约束的转换

在区间数优化中，通常采用区间可能度水平对区间不确定约束进行描述[7]。对于乘员约束系统不确定性问题式(1)中≤型的不等式约束，可转换为如下的确定性不等式约束:

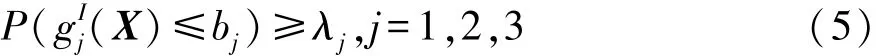
式中:λj为一预先给定的可能度水平，对于实际的工程问题一般取值为1；(X)为乘员约束系统不确定性约束函数；bj为第j个不确定约束的允许上限。(X)在任一确定的X处由不确定性向量U造成的可能取值区间为

一旦求得(X)，即可通过式(7)求解约束可能度P((X)≤bj)，并判断约束可能度是否满足给定的可能度水平。

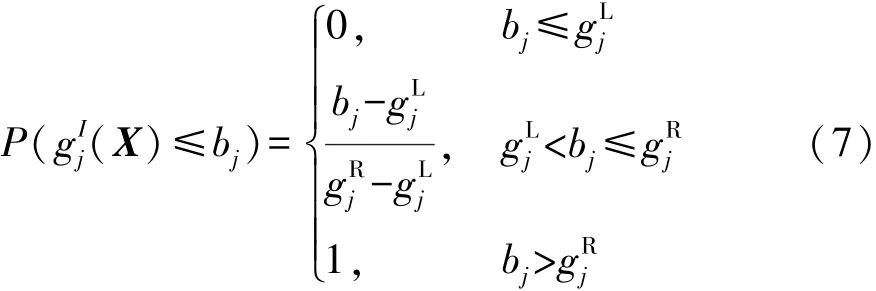
3.3 转换后的确定性优化问题

基于线性加权法和罚函数法对目标函数和约束函数进行处理，式(1)可进一步转换为如下以罚函数fPi(X)表示的无约束多目标优化问题:

其中

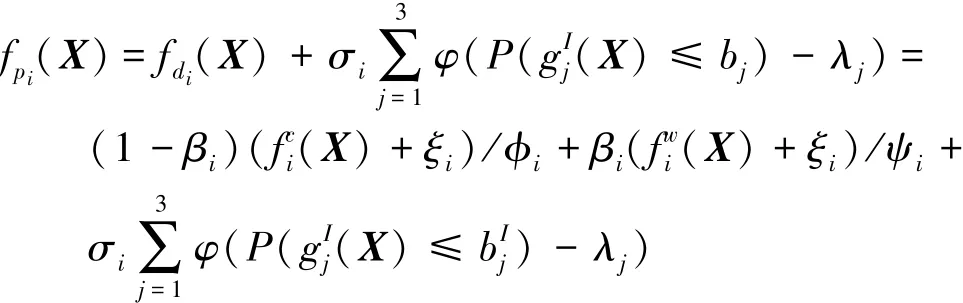
式中:fdi为目标评价函数；0≤βi≤1 为权系数；ξi为保证(X)＋ξi和(X)＋ξi非负的参数；ϕi和 ψi为正则化因子，实际应用中，可依据各自目标同一量级的值进行选取；σi为罚因子；φ为罚函数。φ可通过式(9)获得:

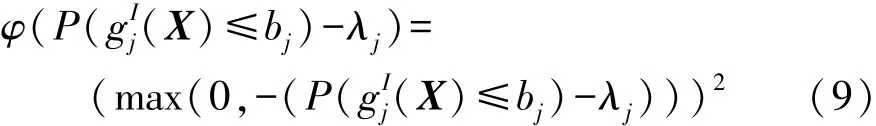
3.4 近似优化问题的建立和求解

由于真正对于优化过程起主要作用的是目标函数和约束在设计向量处的上界和下界，所以本节基于局部加密近似模型技术将依据迭代步获得的部分近似设计点来加密样本，着重提高目标函数和约束函数近似模型在区间边界处局部区域的精度，从而提高优化结果的精确性。采用径向基函数[8]可获得乘员约束系统近似确定性优化问题如下:

其中

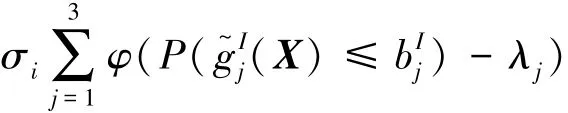
式中:为近似优化问题式(10)的罚函数；为近似目标评价函数。

以上得到的乘员约束系统确定性优化问题属于两层嵌套优化问题，其中外层用来求解最优设计向量，而内层则用来求解不确定目标函数和约束函数的区间。本文中采用全局搜索性能较好的微型多目标遗传算法(μMOGA)[9]和隔代映射遗传算法(IPGA)[10]作为外、内层求解器来求解上述问题。整个求解迭代步骤如下。

(1)利用拉丁超立方采样(Latin Hypercube Design LHD)[11]在设计变量和不确定性变量空间上进行样本点采样，并利用乘员约束系统数值模型计算乘员各项损伤值，从而获得目标函数和约束函数的初始样本。给定允许误差ε＞0，置s＝1。

(2)基于样本点数据，结合径向基函数构建出乘员约束系统近似不确定性优化问题。利用区间序关系转换模型获得如式(10)所示的确定性优化问题，并基于μMOGA和IP-GA的两层嵌套优化算法进行求解，从而获得此近似多目标不确定性优化问题的非支配解集:

(5)计算误差emax:

其中

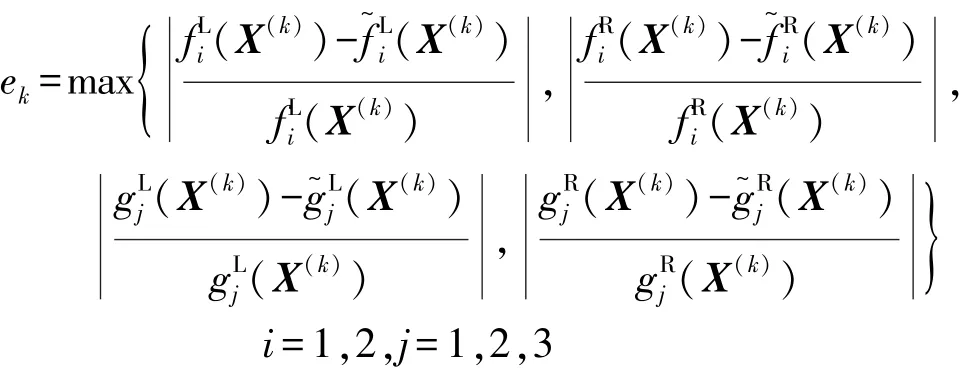
如果emax＜ε，则输出非支配解集，迭代终止；否则，转下步。

(6)把非支配解集对应的目标函数两个边界坐标点(X(k)，)和(X(k)，)作为新样本加入到目标函数样本集；同理，对应于每一个约束的两个边界坐标点(X(k)，)和(X(k)，)也加入此约束的当前样本集，转至步骤(2)，并置 s＝s＋1。

具体优化流程图如图5所示。

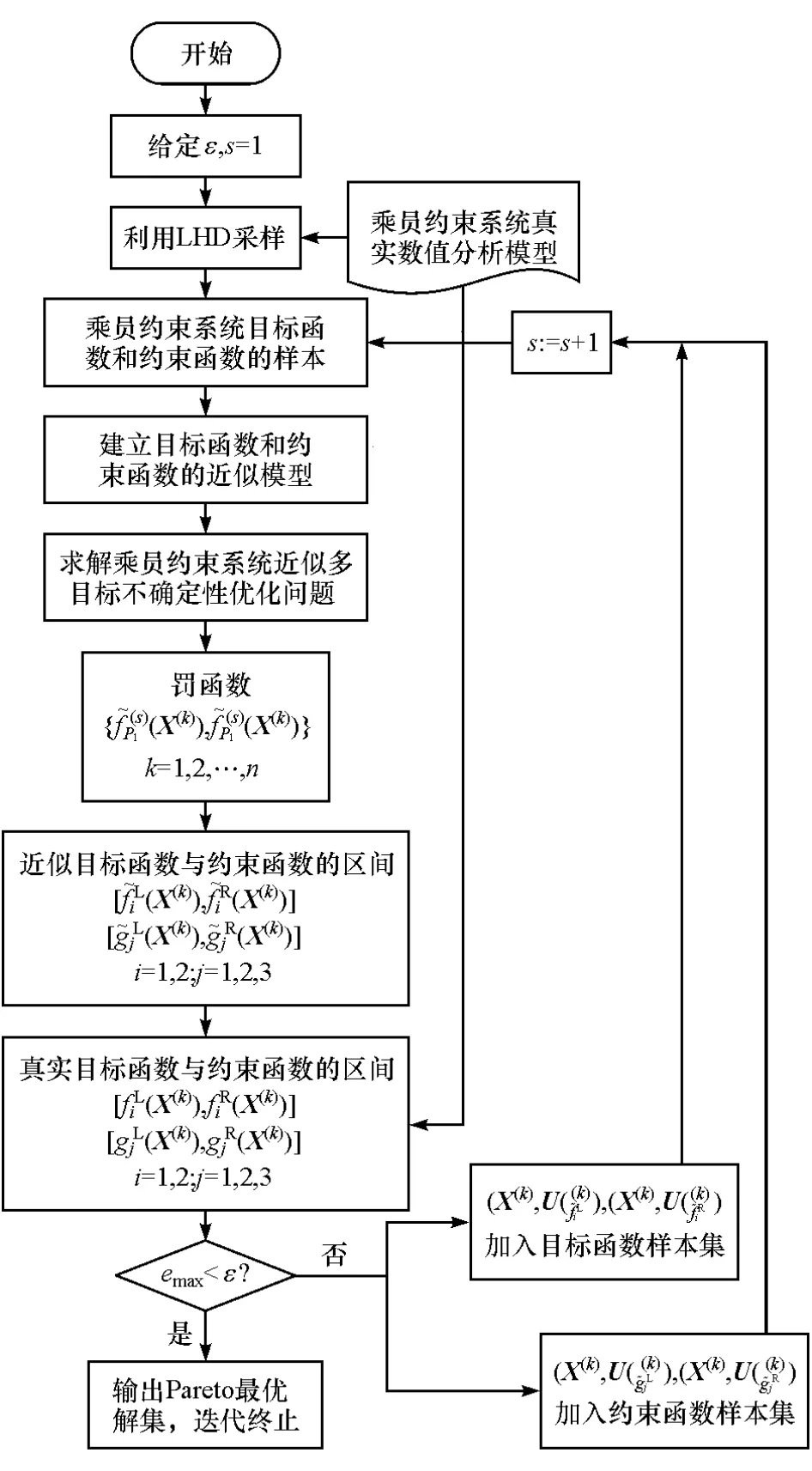
图5 乘员约束系统多目标不确定性优化流程

4 优化结果与分析

整个优化过程中，允许误差ε为15%，目标函数和约束函数的初始样本点为80个，采用μMOGA和IP-GA对式(10)所描述的多目标优化问题进行求解。优化过程中，相关的参数设置如下:ξ1＝ξ2＝0，正则化因子 ϕ1＝ϕ2＝1.0和 ψ1＝ψ2＝1.0，权系数 β1＝β2＝0.5。

在第1个迭代步中，设置外层μMOGA的迭代次数为200代，内层IP-GA的迭代次数为100代。基于初始样本点可获得多目标优化问题Pareto最优解集，如图6所示。

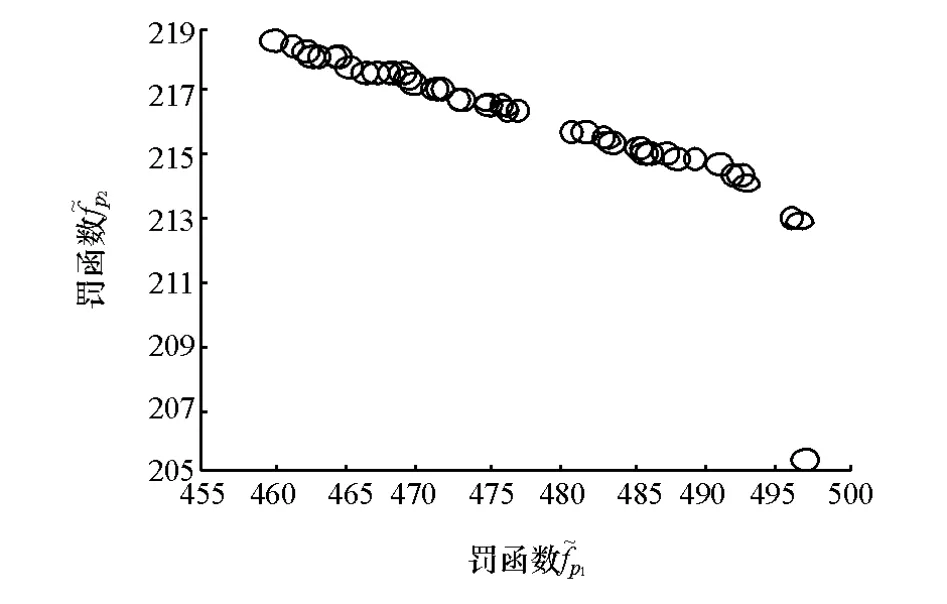
图6 第1个迭代步的Pareto最优解集(样本点80个)

在样本点加密过程中，只要测得Pareto最优解集中的优化值与仿真值之间的最大误差超过许用误差值，即把该优化解作为样本点加入到原样本空间中去，然后进行下一步迭代。表2为设计向量X在(0.84405，－0.00968，0.06123)处的各项目标函数和约束函数值。从表2可以看出，目标函数和约束函数的优化值与仿真值之间的最大误差达到34.5%，超过了许用误差值15%，说明此时的目标函数和约束函数的近似模型相对粗糙，因此把边界样本点:(0.84405，－0.00968，0.06123，0.0，0.9)，(0.84405，－ 0.00968， 0.06123， － 0.05， 1.0)， (0.84405，－0.00968， 0.06123， 0.0， 1.0) 和 (0.84405，－0.00968，0.06123，－0.05，0.9301)作为新的样本点加入到原有的样本空间中去，从而构建更精确的近似模型。

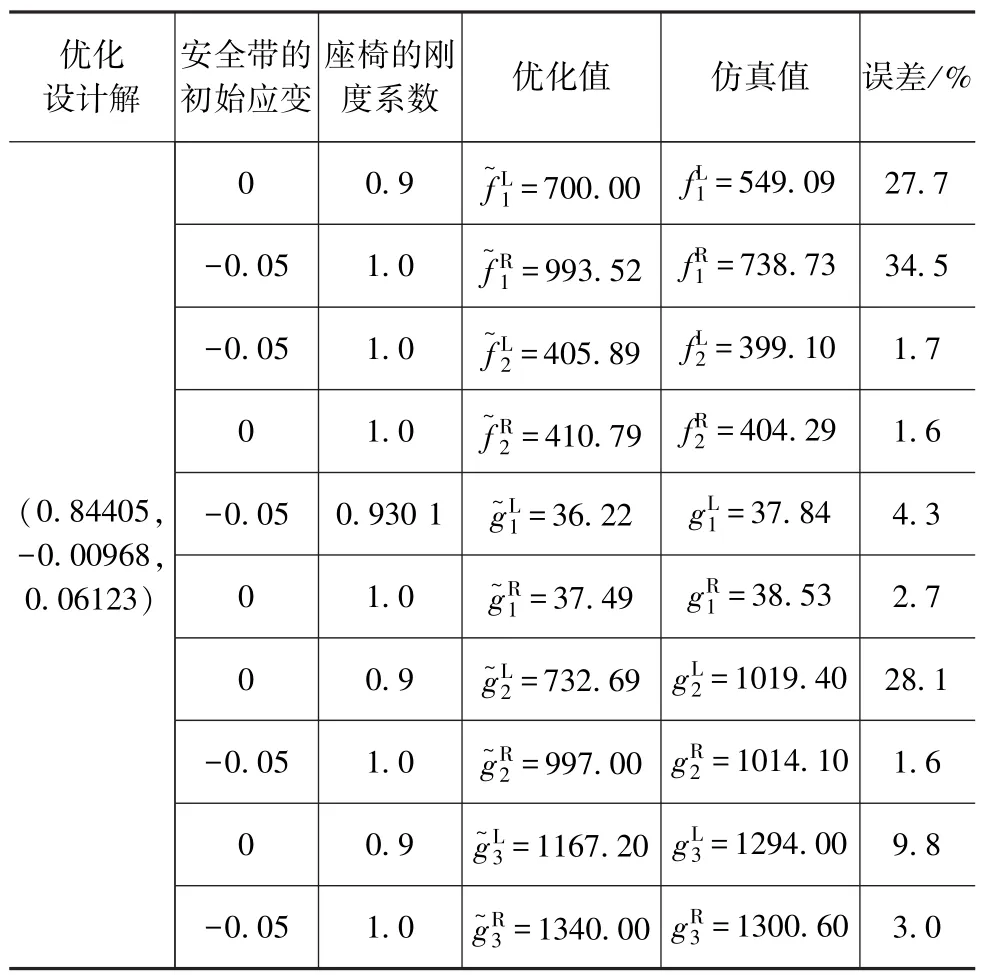
表2 设计向量X＝(0.84405，－0.00968，0.06123)对应的优化结果

在第2个迭代步中，内、外层迭代次数均设为100代。基于84个样本点可获得多目标优化问题Pareto最优解集，如图7所示。通过计算可发现此迭代步的Pareto最优解集对应的目标函数和约束函数的优化值与仿真值之间的最大误差均低于许用误差值。而且，在当前Pareto最优解集中，各项乘员损伤值均在乘员耐受极限范围内，因此优化结果达到设计要求。最后可根据经验或工程人员的偏好选择其中的某一个解作为最优解。表3列出了设计向量 X 在(0.84317，－0.00997，0.06510)处的各项目标函数和约束函数值的区间。从表3可以看出，乘员头部、胸部和腿部的损伤区间均未超过人体耐受极限范围，说明乘员约束系统达到保护乘员的目的。

图7 第2个迭代步Pareto最优解集(样本点84个)

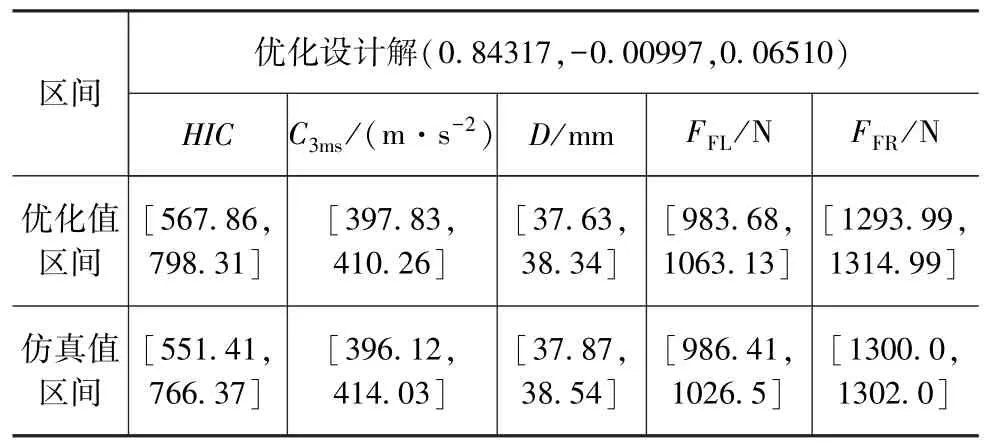
表3 设计向量X＝(0.84317，－0.00997，0.06510)对应的优化结果

5 结论

针对乘员约束系统不确定性参数对乘员安全性的影响，基于区间序关系将不确定性优化问题转换为确定性优化问题，并利用局部加密近似模型技术快速求解目标函数和约束函数的区间，从而获得了满足乘员约束系统安全性的Pareto最优解集。该方法不但能有效提高乘员约束系统的防护性能，而且在汽车安全领域具有广泛的工程应用价值。

[1] 洪亮，葛如海.正面碰撞中基于新型前排安全座椅的后排约束系统优化研究[J].汽车工程，2015，37(11):1277－1283.

[2] 张斌，杨济匡，张维刚，等.轿车侧面安全气囊匹配设计与优化研究[J].汽车工程，2009，31(9):848－853.

[3] 蒋小晴，杨济匡，肖志.基于车身结构与约束系统集成优化的乘员胸部保护研究[J].汽车工程，2013，35(4):369－374.

[4] 葛如海，臧绫，王浩涛，等.汽车座椅坐垫倾角对正面碰撞乘员保护影响分析[J].机械工程学报，2009，45(11):230－234.

[5] VIANA F A C，SIMPSON T W，BALABANOV V，et al.Metamodeling in multidisciplinary design optimization:How far have we really come?[J].AIAA Journal，2014，52(4):670－690.

[6] 龙腾，郭晓松，彭磊，等.基于信赖域的动态径向基函数代理模型优化策略[J].机械工程学报，2014，50(7):184－190.

[7] JIANG C，HAN X，LIU G R.A nonlinear interval number programming method for uncertain optimization problems[J].European Journal of Operational Research，2008，188:1－13.

[8] ZHAO Z H，HAN X，JIANG C，et al.A nonlinear interval-based optimization method with local-densifying approximation technique[J].Structural and Multidisciplinary Optimization，2010，42:559－573.

[9] LIU G P，HAN X，JIANG C.A novel multi-objective optimization method based on an approximation model management technique[J].Computer Methods in Applied Mechanics and Engineering，2008，197:2719－2731.

[10] LIU G R，HAN X.Computational inverse techniques in nondestructive evaluation[M].Florida:CRC Press，2003.

[11] YANG R J，WANG N，THO C H，et al.Metamodeling development for vehicle frontal impact simulation[J].Journal of Mechanical Design，2005，127:1014－1020.