基于脑电信号的疲劳驾驶状态研究∗

陈骥驰，王 宏，王翘秀，化成城，刘 冲

(东北大学机械工程与自动化学院，沈阳 110819)

前言

近年来，随着我国的汽车保有量急剧增加，交通事故也大幅增多，其中，疲劳驾驶是导致交通事故的主要因素[1－2]。近期有关汽车驾驶研究表明，疲劳驾驶状态下发生事故或接近发生事故的概率是清醒驾驶状态下的4～6倍[3－4]。当驾驶员疲劳时，驾驶员对外界环境的注意力和反应能力都会降低，从而可能引发严重事故[5]。因此，开发车载疲劳干预系统，对驾驶员和车辆运行状态进行实时监控并择机进行干预被视为预防疲劳驾驶的核心技术，如何准确快速检测驾驶员驾驶疲劳状态成为值得研究的重要课题。

检测疲劳驾驶状态一般可从主观和客观两方面进行研究。常用的主观检测方法有多维尺度分析法、成对比较法(pairwise comparison，PC)和排序法等[6]，但主观检测方法由于受驾驶员和研究者主观判断能力的影响，在检测疲劳状态时有一定的局限性，一般作为辅助方法使用。与传统的主观评价方法相比，利用生理电信号来评价驾驶员驾驶疲劳状态能做到客观准确、采集方便和使用条件限制少，是一种较有前景的研究疲劳影响的方法。文献[7]中基于驾驶期间的心率变异性并结合转向盘握力来评估驾驶员的疲劳程度。然而，在众多生理信号中，脑电(electroencephalogram，EEG)具有较高的时间分辨率和精度，更适合评价疲劳效应[8－9]。文献[10]中利用汽车模拟驾驶系统并记录其脑电分析特征量，进而分析平均功率谱密度比R和关联维数D，以评价驾驶员疲劳程度。文献[11]中利用汽车模拟驾驶系统提出一种基于独立分量分析的脑电疲劳状态判断方法，进而求得信号的功率谱密度，从而获得各波段脑波的相对能量值，判断驾驶员的疲劳程度。然而，现有的研究方法主要基于功率和能量熵等，这类方法与振幅相关，其性能易受到EEG振幅的影响，且驾驶员利用汽车模拟驾驶系统采集到的脑电信号与在真实车辆中采集到的相比，由于缺少了转向盘力反馈以及在车速变化时驾驶员的感知，在一定程度上影响脑电信号的分析结果。

为克服这一问题，并提高疲劳检测精度，本文中选取真实驾驶环境，利用便携式脑电采集设备Emotiv，实时采集驾驶员的脑电信号，并对其进行小波包分解与重构，提取各个节律信号，然后分别计算各导联间的相位迟滞指数来构建连接矩阵，并提取脑网络特征。通过对驾驶员主观疲劳度与所提取特征的神经网络回归分析，最终得到二者间的复杂关系。研究结果表明，该方法对驾驶员疲劳检测系统的开发具有重要意义。

1 实验

1.1 实验方案

选取8名男性驾驶员(编号为A～H)，年龄在26～33周岁，身体健康，视力正常，无任何神经病史。要求驾驶员在实验前将头发清洗干净，维持正常睡眠时间，在实验过程中不饮用任何类型的刺激饮料，如酒精、茶或咖啡等。文献[12]中利用汽车模拟驾驶器研究驾驶员在50min脑电特征变化，并分别将前后各10min脑电信号标记为清醒状态和疲劳状态。因此本实验设计如下:实验时间选为晴天中午，驾驶路线从东北大学南湖校区沿G1501高速至沈阳怪坡风景区，驾驶时间约1h。对每位驾驶员脑电信号进行两次采集，采集时间分别是在开始驾驶的3min和结束时的3min，这两个时间段分别对应驾驶员的清醒状态和疲劳状态。实验流程如图1所示。文献[13]中使用Emotiv设备通过脑电信号检测情绪，从脑电信号中提取特征，以便在二维情感模型中表征心理状态，得到较好结果。考虑到该设备具有成本低、对被试者影响小等优点，因此采用Emotiv脑电采集分析系统对驾驶员两种状态下的脑电信号进行了记录。 导联分别为 AF3，F7，F3，FC5，T7，P7，O1，O2，P8，T8，FC6，F4，F8 和 AF4，电极按照 10－20国际标准放置，其布置如图2所示。采样频率为128Hz。

图1 真实驾驶实验流程

1.2 数据处理

由于真实驾驶环境中采集到的脑电信号会含有一定的干扰，首先使用EEGLab工具包，对信号进行去噪。包括伪迹去除和基线校正，并使用独立分量分析(independent component analysis，ICA)方法去除眼电干扰。实现对采集的脑电信号的预处理[14]。

为提取脑电信号中δ，θ，α和β节律信号，本文中选取小波包分解与重构方法，该方法可克服小波变换的频率分辨率随信号频率的升高而降低的缺陷，并能对信号进行更加精确地分析，从而更好地反映信号本质特征[15]。以f(t)表示原始信号，经小波包分解后，在第i分解层得到2i个子频带，故原始信号f(t)可表示为

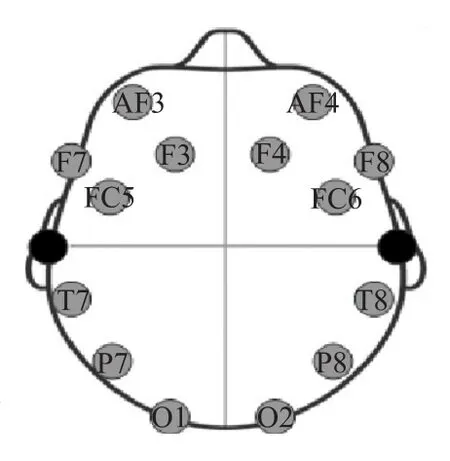
图2 采集脑电信号的脑部导联示意图

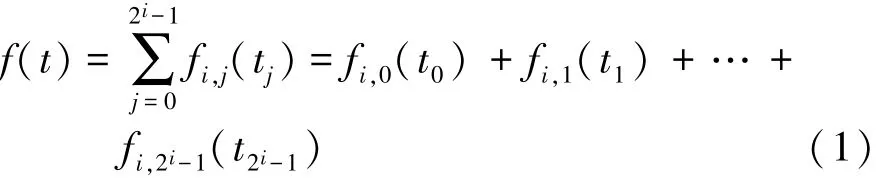
式中:j＝0，1，2，…，2i－1；fi，j(tj)为小波包在第 i层节点(i，j)上分解的重构信号。本文中对频带进行4层分解，提取信号中 δ(0－4Hz)，θ(4－8Hz)和 α(8－12Hz)节律，并重构β(12－32Hz)节律。F7导联的小波包分解与重构的结果如图3所示。

图3 脑电信号的小波包分解与重构

2 数据特征提取与分析

通过计算两信号之间的同步似然值(synchronization likelihood，SL)可评判信号之间的非线性相关程度[16]。但在EEG信号采集过程中容易产生容积传导问题，而SL法可能在两组信号间产生虚假的高相关性[17]。相位迟滞指数(phase lag index，PLI)讨论两信号之间的相位同步性，对容积传导现象不敏感，可避免产生虚假的高相关性，能对信号之间的非线性耦合程度提供一种可靠的评价指标。因此，本文中采用PLI来构建不同导联信号之间的非线性相关性。

2.1 相位迟滞指数分析

相位分析通过检查信号之间的瞬时相位的关系，避免了振幅对分析结果的影响，该方法已被证明是推断神经连接性的有效方法。对任意的EEG信号x(t)，其解析信号xA(t)可通过一复杂函数定义[17]为

式中:xH(t)为x(t)的希尔伯特变换(Hilbert transform)。定义瞬时相位φ(t)为

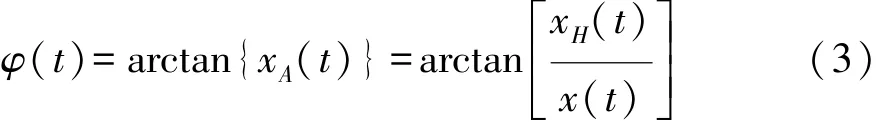
则任意两个导联的时域信号ϕm(t)和ϕn(t)的瞬时相位差 ϕm，n(t)可表示为

将PLI定义为是对这个相位差分布的不对称测量值，即

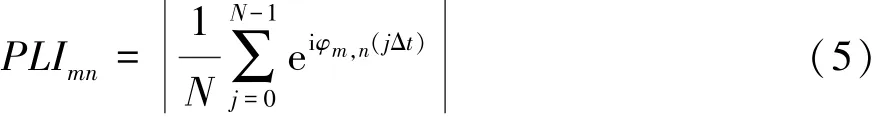
式中:N为采样点数；PLImn的范围为0～1，PLI＝0表明两组信号之间没有相位同步，PLI＝1表明相位严格同步于一个常数，并且延迟为0。

2.2 非线性脑网络参数分析

图(graph)提供了一种用抽象的点和线表示各种实际网络的统一方法，图论分析方法是以图为研究对象的数学方法，因此也成为目前研究复杂网络的一种共同的语言。这种抽象的一个主要好处在于有可能透过现象看本质，通过对抽象的图的研究而得到具体的实际网络的拓扑性质(topological property)[16，18]。本文中将脑电信号的通道定义为节点，通道间的相关值定义为边连接值，图对应的邻接矩阵则由该边连接值表示。清醒和疲劳状态下总平均邻接矩阵如图4所示。

该矩阵为14×14方阵，横轴和竖轴分别对应全脑区各个导联，每个节点表示各个导联信号之间的相位滞后指数值，该值介于0到1之间，若两个导联之间的相位同步性越强，其值越趋近于1。从图4可以看出，相比清醒状态，疲劳时PLI值有所减小，且这种减小趋势在θ，α和β节律段比较明显。

聚类系数和特征路径长度是图的两个最基本的特征量[14]，文献[19]中利用聚类系数和特征路径长度这两个参数来描述急性抑郁患者的睡眠脑网络变化，并得到较好的分析结果。因此，本文中采用聚类系数和特征路径长度来对比驾驶员清醒和疲劳时的脑网络特性。网络的聚类系数(clustering coefficient，C)定义为网络所有节点的聚类系数的平均值，即

图4 清醒和疲劳状态下总平均邻接矩阵

式中:N为网络中的节点数；Ci为网络中一个节点i的聚类系数。

式中:ki为节点i的度，即无向网络中其他节点与该节点直接相连的边的数目；Ei为节点i与ki个邻居节点间实际存在的连接边数；分母ki(ki－1)/2为该节点与邻居节点可能存在的最大边数。聚类系数用于测量复杂网络的连接性，较高的聚类系数说明网络在某些区域具有较为密集的连接。

网络的特征路径长度(characteristic path length，L)定义为整个网络中任意两个节点最短路径长度的平均值，即

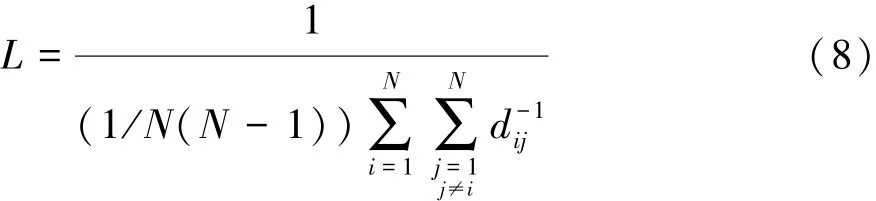
式中dij为连接节点i和节点j的最短路径上的边的数目。节点间的相互作用即为神经元间的相互作用，反映神经元递质的传递，是脑网络认知过程中信息传递和处理的基础[20]。特征路径长度越短，表明脑网络中连接距离较远的两个节点所需的边数越少。

为更加直观地观察到不同状态下脑网络连通性的变化，须对邻接矩阵选择一个合适的阈值，滤掉矩阵中小于该阈值的元素。图5为选取阈值0.32后得到的各个节律的脑网络拓扑图。从图5可以看出，清醒状态和疲劳状态之间的功能连通性存在明显不同，值得注意的是，在θ，α和β节律段，与清醒状态相比，疲劳状态下前额极至顶极和额极至枕极的功能连通性被削弱。由此可以推测，前额极至顶极EEG功能连通性将反映前额极至顶极区域的感觉信号，前额极至顶极功能连通性可以由前额极至顶极信号主动调节，随着驾驶时间增加，驾驶员疲劳程度增加，这些信号强度有所降低，导致连通性变差。为定量比较清醒和疲劳状态的特征，计算各个节律对应的聚类系数和特征路径长度，如图6所示。从图6(a)可以看出，在各个节律段，与清醒状态相比，疲劳状态下聚类系数均有所减小，特别是在α和β节律段，下降幅度较为明显。从图6(b)可以观察到，在各个节律段，疲劳状态下特征路径长度比清醒状态下有所增加。

3 脑电特征与疲劳的相关分析

3.1 主观评价方法

通过成对比较法(PC)获取驾驶员对自身疲劳程度的评价。PC法以驾驶员驾驶前后的疲劳程度的比较为基础，采用1～9比例标度法进行评判，1表示A和B一样疲劳；3表示A略微疲劳；5表示A比较疲劳；7表示A很疲劳；9表示A非常疲劳；而2，4，6和8则分别表示相邻评判的中间状态。

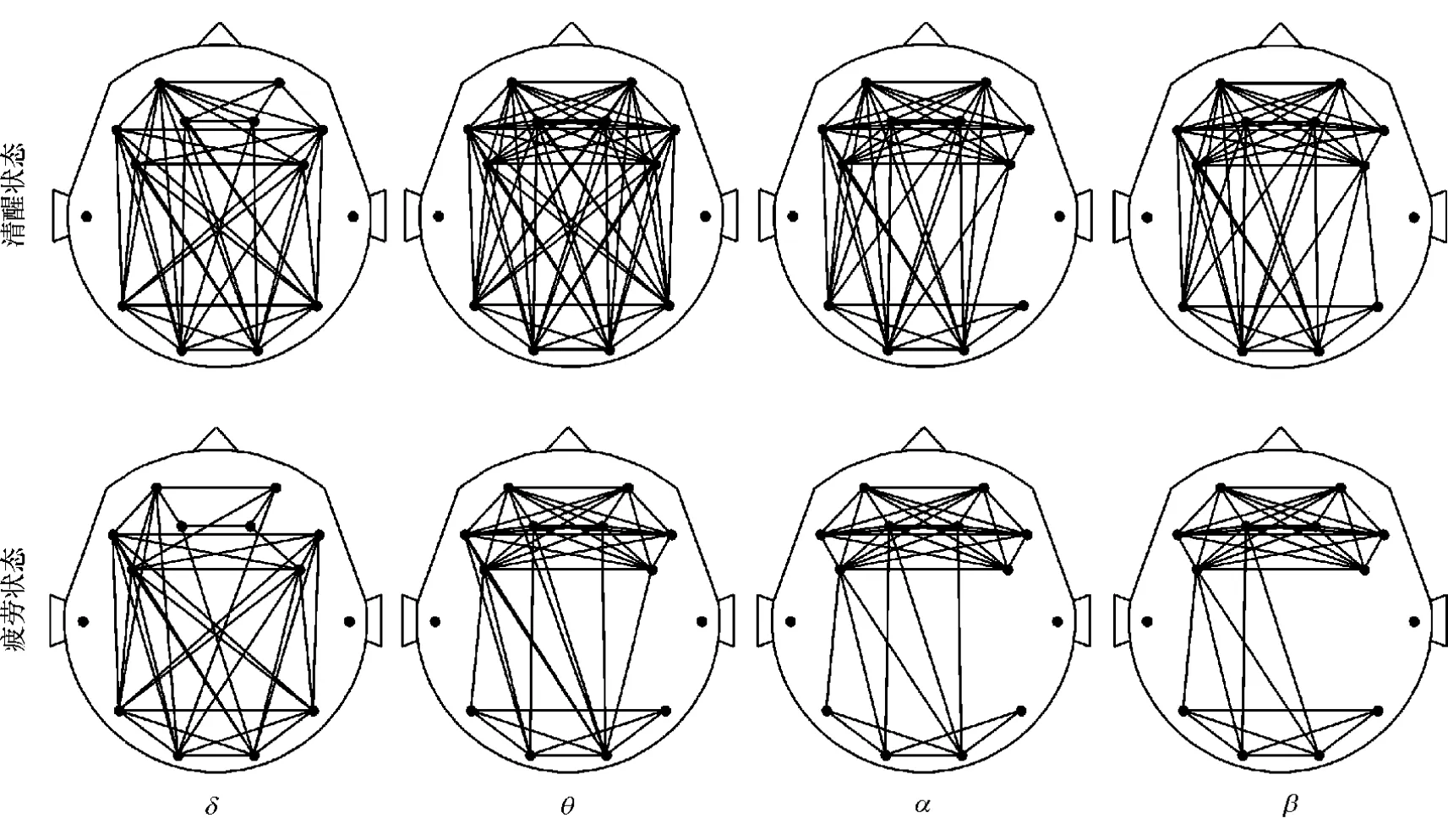
图5 清醒和疲劳状态下脑网络拓扑图

图6 脑网络聚类系数和特征路径长度

3.2 脑网络特征参数与主观疲劳程度相关分析

采用一个含有多层的人工神经网络(artificial neural network，ANN)算法。将8名驾驶员的脑电数据每隔1min截取一段，将其中80%的样本数据作为训练集，其余20%的样本数据作为测试集。其中网络的输入为δ，θ，α和β节律下的聚类系数和特征路径长度这8个脑网络特征参数，输出为主观疲劳度。网络的输出如下式所示:

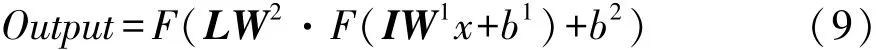
式中:IW1为输入层的权重矩阵；LW2为隐含层的权重矩阵；x为脑网络特征参数；b1，b2为偏移量；Output为训练的输出，函数F采用Sigmoid激活函数。主观评价得到的疲劳度与神经网络输出的相关性如图7所示，R为95.605%，表示疲劳度与神经网络输出相关性较高。将其余20%的测试集样本数据输入该系统，得到主观评价的疲劳度与神经网络输出的相关性，如图8所示，R为90.27%。不难看出，驾驶员的疲劳度可以由训练得到的神经网络输出有效估计。

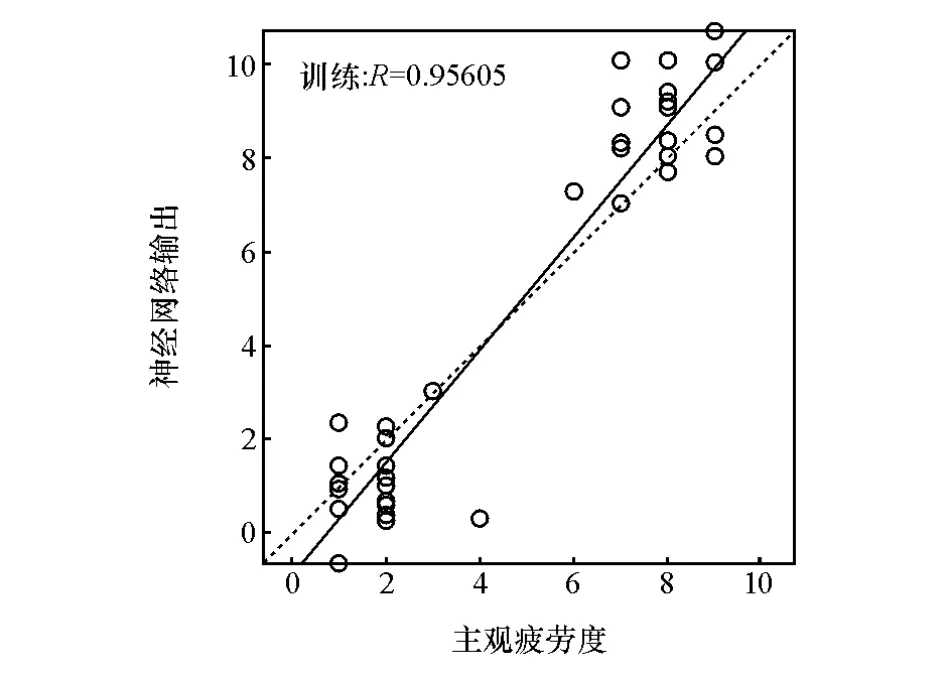
图7 训练集主观疲劳度与神经网络输出的相关性

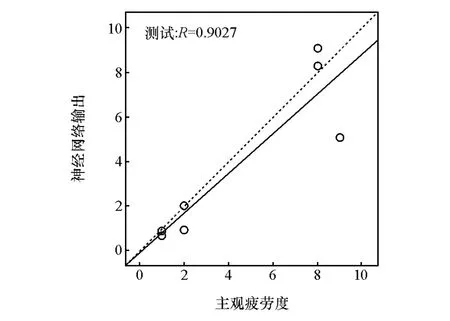
图8 测试集主观疲劳度与神经网络输出的相关性

4 结论

基于脑电信号完成了在真实路况下的疲劳驾驶实验，通过小波包分析得到了δ，θ，α和β节律信号，计算了清醒与疲劳状态下各导联信号之间的相位迟滞指数，并基于此构建了功能性脑网络，采用人工神经网络算法得到各个节律下聚类系数和特征路径长度与主观疲劳度间的复杂关系。结果表明，与清醒状态相比，疲劳状态下前额极至顶极和额极至枕极的功能连通性被削弱，并通过神经网络成功实现了利用客观脑网络特征参数估计主观疲劳度，相关性R为90.27%，回归分析结果证明了基于功能连接的精神疲劳评估方法的可行性，为不同精神状态下建立脑动态模型开辟了新的途径。今后的研究可考虑结合脑电、眼电和肌电信号，通过多源信息融合进一步提高驾驶员疲劳检测系统精度。

[1] FU R R，WANG H，ZHAO WB.Dynamic driver fatigue detection using hidden Markov model in real driving condition[J].Expert Systems With Applications，2016，63:397－411.

[2] WASCHER E， GETZMANN S， KARTHAUS M.Driver state examination—treading new paths[J].Accident Analysis and Prevention，2016，91:157－165.

[3] 马勇，付锐.驾驶人视觉特性与行车安全研究进展[J].中国公路学报，2015，28(6):82－94.

[4] 胥川，裴赛君，王雪松.基于无侵入测量指标的个体差异化驾驶疲劳检测[J].中国公路学报，2016，29(10):118－125.

[5] 张宁宁，王宏，付荣荣.基于小波熵的驾驶疲劳脑电信号特征提取[J].汽车工程，2013，35(12):1139－1142.

[6] 陈剑，杨雯，李伟毅.汽车声品质主观评价试验方法探究[J].汽车工程，2009，31(4):389－392.

[7] ROGADOE，GARCÍA JL，BAREA R，et al.Driver fatigue detection system[C].IEEE International Conference on Robotics＆Biomimetics，2009:1105－1110.

[8] KAR S，BHAGAT M，ROUTRAY A.EEG signal analysis for the assessment and quantification of driver's fatigue[J].Transportation Research Part F，2010，13:297－306.

[9] 王福旺，王宏.长途客车驾驶员疲劳状态脑电特征分析[J].仪器仪表学报，2013，34(5):1146－1152.

[10] 彭军强，吴平东，殷罡.疲劳驾驶的脑电特性探索[J].北京理工大学学报，2007，27(7):585－589.

[11] 李明爱，张诚，杨金福.一种基于脑电信号的疲劳驾驶状态判断方法[J].北京生物医学工程，2011，30(1):57－61.

[12] MU Z D，HU JF，MIN JL.Driver fatigue detection system using electroencephalography signals based on combined entropy features[J].Applied Sciences，2017，7(2):150.

[13] RAMIREZ R，VAMVAKOUSIS Z.Detecting emotion from EEG signals using the Emotive Epoc device[J].Lecture Notes in Computer Science，2012，7670:175－184.

[14] DELORME A，MAKEIG S.EEGLAB:An open source toolbox for analysis of single-trial EEG dynamics including independent component analysis[J].Journal of Neuroscience Methods，2004，134(1):9－21.

[15] 吴定超，王珂，马喜来，等.基于小波包分解和特征能量提取技术的车内传导干扰源识别[J].汽车工程，2008，30(12):1103－1107.

[16] STAM C J，REIJNEVELD JC.Graph theoretical analysis of complex networks in the brain[J].Nonlinear Biomedical Physics，2007，1(3):1－19.

[17] STAM C J， NOLTE G， DAFFERTSHOFER A.Phase lag index:assessment of functional connectivity from multi channel EEG and MEG with diminished bias from common sources[J].Human Brain Mapping，2007，28(1):1178－1193.

[18] WANGSQ，SONGQY，WANGX W，et al.Rate and power adaptation for analog network coding[J].IEEE Transactions on Vehicular Technology，2011，60(5):2302－2313.

[19] LEISTEDT SJ， COUMANSN，DUMONT M.Altered sleep brain functional connectivity in acutely depressed patients[J].Human Brain Mapping，2009，30:2207－2219.

[20] BULLMORE E，SPORNSO.Complex brain networks:Graph theoretical analysis of structural and functional systems[J].Nature Reviews Neuroscience，2009，10(3):186－198.