反比例函数的图象与性质教学设计

甘肃省会宁县河畔初级中学 李晓菊

学习目标：

1.进一步熟悉作函数图象的步骤，会作反比例函数的图象。

2.逐步提高从函数图象中获取信息的能力，探索并理解反比例函数的主要性质。

3.会作反比例函数的图象，培养学生的作图能力并能理解反比例函数的性质。

学习重点：

反比例函数的图象和性质。

学习难点：

理解反比例函数的性质。

学习过程：

一、自主学习

1.回忆画函数图像的一般过程：______________，_______。

2.（1）一次函数y=kx+b（k≠0）的图像是

（2）当k>0时，y随x的增大而

当k＜0时，y随x的增大而

列表：

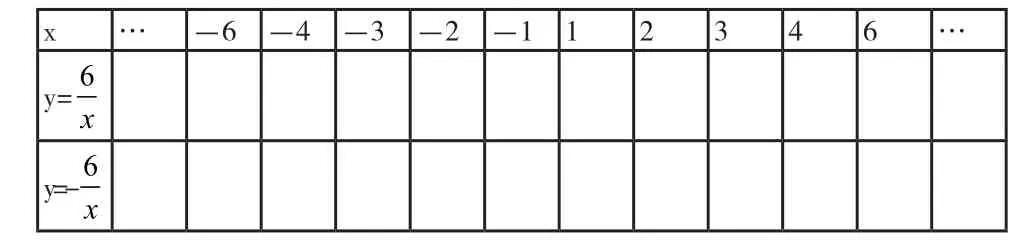
x …－6 －4 －3 －2 －1 1 2 3 4 6 …y=6 x y=-6 x

描点：以表中各组对应值作为点的坐标，在直角坐标系内描出相应的点。

连线：用光滑的曲线顺次连结各点，即可得到函数的图象

4.观察函数的图象，它们有什么相同点和不同点？

二、小组合作、归纳总结

反比例函数的图象是由两支_____组成的.（通常称为_____）

当k＞0时，两支曲线分别位于第_____象限内，在每一象限内，的值x随值的增大而_____;

当k＜0时，两支曲线分别位于第_____象限内，在每一象限内，的值x随值的增大而_____;

两个函数图象都是_____对称图形，它们各自都有_____条对称轴。

反比例函数关系式可以写成以下三种形式：y=kx-1，xy=k （ k为常数k≠0）

（注：说明x, y, k三者都不为零的原因，由此来加强理解反比例函数图象永远不会和两坐标轴相交）

三、例题分析

1.反比例函数的图象经过点（-2，4），求它的解析式，并画出函数图象，图象分布在哪几个象限？点（2，-4）在函数图象上吗？函数值y随x值的变化是如何变化的？

2.已知点P、Q在反比函数的图象上，不画出函数图象，你能解决以下问题吗？

(1)若P(1，a)，Q (2，b), 比较a、b的大小；

(2)若P(-1，a)，Q(-2，b)，比较a、b的大小；_______；

(3)若P(x1，y1),Q(x2，y2)，x1＜x2，你能比较 y1与y2的大小吗？ .

四、巩固练习

1.如果点P（a，b）在的图象上，那么在此图象上的点还有（ ）

A（－a，b） B.（a，－b） C.（－a，－b）D.（0,0）

2.已知变量y与x成反比例，并且当x＝2时，y＝－3。（1）求y与x的函数关系式；（2）当y＝2时x的值；

3.已知反比例函数的图象在第二、四象限内，函数图象上有两点则y1与y2的大小关系为（ ）

A. y1＜y2B.y1=y2C.y1>y2D.无法确定

4.若函数y=(m-1)是反比例函数,则m的值等于( )

A.±1 B.1 C.D.-1

5.已知反比例函数当x=1时，y=-8. 新|课 |标|第 网

（1）求k的值，并写出函数关系式；

(2)点P、Q、R在函数图象上，填空：P(1，_), Q(2，_), R(_,-8)；（3）点P’、Q’、R’分别是点P、Q、R关于原点的中心对称点，写出点P’、Q’、 R’的坐标；

五、全班交流学习

1.已知y与2x—1成反比例,且当x=1时,y=2,那么当x=0时,y=________；

2.已知一次函数y=kx+b的图象经过第二、三、四象限，则反比例函数的图象在（ ）

A.第一、二象限; B.第三、四象限; C.第一、三象限; D.第二、四象限.

3.已知反比例函数的图象上有两点P(1，a)，Q(b，2.5).

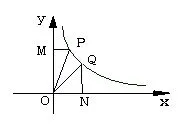
(1) 求a、b的值；(2) 过点P作y轴的垂线交于点M，求△PMO的面积；

(2) 过点Q作x轴的垂线交于点N，求△QNO的面积；

(3)过双曲线上任意一点A(m, n)作x轴(或y轴)的垂线，垂足为B，

求△ABO的面积

(4)你发现了什么规律？

六、课堂小结

反比例函数的图象和 性质：

（1）反比例函数（k为常数，k≠0）的图象是双曲线.

（2）当k>0时，双曲线的两支分别位于第一、第三象限，在每个象限内，y的值随x值的增大而减小.

（3）当k＜0时，双曲线的两支分别位于第二、第四象限，在每个象限内，y的值随x值的增大而增大。

七、作业布置

课后习题1、2题。

八、教学反思