预控破片战斗部成型及速度衰减的影响研究

郭策安，周 峰，赵 爽，石小山，石 阔，张 健

(1.沈阳理工大学 装备工程学院，沈阳 110159；2.国营第五二四厂，吉林 吉林 132021)

在现代战争中，普通战斗部对大型、防护低的装甲运兵车、侦察车、指挥车、地面装备器材和人员等目标的毁伤效率较低。采用预控破片战斗部的杀伤爆破弹，使破片数量大量增加，在保证毁伤效能的前提下，大大提高了命中率，现已成为国内外学者的研究热点[1-6]。

在预控破片战斗部研究方面，吴成等利用理论计算与实验对比的方法，得出内刻V形槽战斗部壳体的临界断应变判据[7]。朱桂利等利用有限元软件LS-DYNA对预控破片冲击圆管的过程进行仿真模拟，并通过实验验证，得出破片在侵彻过程中的速度变化规律及圆管壁厚和预控破片的长径比对极限穿透速度影响规律[8]。印立魁等利用有限元软件AUTODYN对立方体预控破片战斗部的爆炸驱动过程进行仿真模拟，建立了立方体破片速度计算模型[9]。彭正午等利用有限元软件AUTODYN对壳体外刻槽的预控破片战斗部在不同槽深和槽宽时的破片形成过程进行数值模拟，得出槽深和槽宽对预控破片成型的影响规律[10]。

与普通战斗部相比，预控破片战斗部可以大大提升炸药的利用率。本文基于LS-DYNA有限元软件对内刻V形槽预控破片战斗部的成型过程进行仿真模拟，利用量纲分析的方法[11-14]，得出刻槽深度与刻槽角度对成型后有效破片数量及平均速度的影响，进而得出速度衰减规律，并通过试验验证其正确性。

1 有限元模型建立

1.1 网格划分及边界条件

根据仿真模拟环境，建立V型槽预控破片战斗部的四分之一模型。壳体材料采用50SiMnVB，其强度较高、脆性大，同时形成的破片形状较好、速度快、数量多。炸药材料采用8701炸药。沥青漆用于填补V形槽空隙，避免火药气体泄露。设置单面滑移接触。整体采用3DSolid64六面体实体单元，起爆方式采用中心起爆。其战斗部壳体实体图及有限元模型如图1所示。

壳体材料在高温、高压的爆轰气体作用下经历了塑性大变形流动和破碎过程，因此采用Johnson_cook模型来描述战斗部材料的动力学变形及失效行为[15]。

Johnson-cook材料模型的等效应力表达式为

(1)

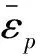
1.2 计算结果分析

V形刻槽的参数主要有刻槽深度和刻槽角度，影响断裂预控破片战斗部破片成型的形状和影响破片速度，因此V形刻槽的深度和刻槽角度作为研究战斗部毁伤效能的一部分。毁伤效能主要看有效破片个数和有效破片的速度(一般认为成型后的破片质量大于0.15g，动能大于79J为有效破片)。图2为预控破片成型过程。由图2可知，预控破片在65μm时，壳体完全裂开。

1.2.1 刻槽深度对预制破片成型的影响

图3为不同刻槽深度战斗部成型后破片图，以战斗部半径(R)为基准，图3展示了刻槽深度为0.04R、0.045R、0.05R、0.055R、0.06R时破片形状。由图3可见，刻槽深度改变，成型后破片形状和数量都不同，刻槽深度为0.04R～0.045R时，在近起爆点处，可以形成规整有效破片，但远离起爆处，出现大量连片情况，预控破片不能形成预想有效破片；刻槽深度为0.05R时，成型后有效破片成型形状良好，出现较少的连片情况，可以形成预想数量和速度的有效破片；刻槽深度为0.055R～0.06R时，在近起爆点处，成型后有效破片质量较小，远离起爆处，连片情况增加。这是因为刻槽的深度决定了壳体承受应力的强度。刻槽深度过深时，壳体容易发生断裂破碎，导致壳体膨胀时间不够，火药气体能量过早的流失，壳体不能满足应力要求，成型后有效破片数量、质量和速度降低。刻槽深度过浅时，则应力在刻槽处的集中不够明显，导致壳体不能沿沟槽断裂，同时大量火药气体作用于壳体断裂，成型后破片出现连片或形状不规则等情况，有效破片数量和速度降低。

图2 预控破片成型过程

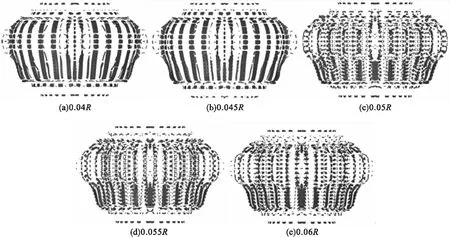
图3 不同刻槽深度成型情况

1.2.2 刻槽角度对预制破片成型的影响

图4为不同刻槽角度战斗部成型后破片图，图4展示了16°、18°、20°、22°、24°时破片形状。

图4 不同刻槽角度成型情况

由图4可见，刻槽角度的改变，成型后破片形状和数量都不同，刻槽角度为16°～18°时，在近起爆点处，形成规整有效破片，但远离起爆点处，出现大量连片情况，不能形成预想数量和速度的有效破片；刻槽角度为20°时，形成大量规整的有效破片，连片情况较少，形成预想数量和速度的有效破片；刻槽角度为22°～24°时，在近起爆点处，成型后有效破片质量较小，远离起爆处，连片情况增加，不能形成预想速度和质量的有效破片。这是因为刻槽角度的增大，使炸药与壳体接触面积变大，从而影响火药气体对壳体的作用，在起爆点附件处，壳体容易快速断裂，导致火药气体过早外泄，从而影响其成型结果。同时刻槽角度过大，壳体质量明显降低，导致有效破片数量和速度明显降低；刻槽角度过小，大量的火药气体能量作用在壳体断裂，导致有效破片数量和速度明显降低。

1.2.3 预制破片成型数量和速度影响研究

讨论刻槽深度和刻槽角度两个因素，分别取5个值，以战斗部半径(R)为基准，相对刻槽深度取0.04R、0.045R、0.05R、0.055R、0.06R；刻槽角度取16°、18°、20°、22°、24°，对其进行仿真模拟计算(共5×5次)。

通过25次仿真模拟，可以得出相对应的刻槽深度、刻槽角度的有效破片数量和有效破片平均速度的计算结果，如表1、表2所示。

由表1可知，当刻槽深度在0.04R～0.045R时，随着刻槽角度的增加成型后的有效破片数量增加，当相对刻槽深度在0.05R～0.06R时，随着刻槽角度的增加成型后的有效破片数量先增加后减少；当刻槽深度较深，刻槽角度越大时，成型后的有效破片数量先增加后减少。

表1 有效破片数量

表2 有效破片平均速度

由表2可知，当刻槽深度在0.04R～0.045R时，随着刻槽角度的增加成型后的有效破片速度增加，当相对刻槽深度在0.05R～0.06R时，随着刻槽角度的增加成型后的有效破片速度先增加后减少；当刻槽深度较深，刻槽角度越大时，成型后的有效破片速度先增加后减少。

2 基于量纲分析的破片速度预测

图5为V型槽预控破片战斗部示意图。影响有效破片数量和有效破片的平均速度的因素主要有：炸药长度(L)、炸药密度(ρz)、炸药质量(M)、战斗部半径(R)、炸药比能(Ee)、爆速(T)、壳体密度(ρk)、壳体厚度(H)、V型槽深度(h)、V型槽角度(θ)。

有效破片数量N和有效破片的平均速度V与这些参数之间的函数关系式为

N=(L,ρz,M,R,T,Ee,γe,ρk,H,h,θ)

(2)

V=(L,ρz,M,R,T,Ee,γe,ρk,H,h,θ)

(3)

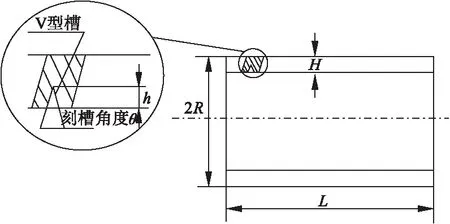
图5 V型槽预控破片战斗部示意图

根据本文选取炸药为8701炸药，炸药密度(ρz)、长度(L)与半径(R-H)不变，因此炸药质量(M)、爆速(T)与炸药比能(Ee)不变；壳体材料选取50SiMnVB，壳体密度(ρk)，壳体厚度(H)不变。上述参数均为独立量纲，即

(L,ρz,M,R,T,Ee,γe,ρk,H)=const

(4)

V型槽角度θ和有效破片数量N为无量纲，将其余参数量纲化，可将公式(2)、(3)改写为

N=f(h/L,θ)

(5)

VTM-1=f(h/L,θ)

(6)

对表1和表2的仿真模拟数据进行二元函数曲面拟合。假设x=h/L，y=θ，有效破片数量和有效破片平均速度的拟合公式为

N=f(x,y)=A1+a1x+b1y+c1x2+d1y2+f1xy

(7)

v0=VTM-1=f(x,y)=A2+a2x+b2y+c2x2+d2y2+f2xy

(8)

将表1、表2的数据带入式(7)、式(8)中，经拟合计算可得公式

N=f(x,y)=-631.36+33662.85714x+39.36714y

-326857.14286x2-0.44643y2-772xy

(9)

v0=VTM-1=f(x,y)=684.28+67076.57143x+19.39y-1.31657x2-0.375y2-152xy

(10)

式(9)、式(10)拟合度为0.95，拟合度较好。利用表1、表2和式(9)、式(10)进行拟合，得到图6、图7二次函数拟合曲面。

对比图6、图7，式(9)、式(10)符合相对刻槽深度和刻槽角度对成型破片的影响趋势，综合考虑，相对刻槽深度为0.05R、刻槽角度为20°时，有效破片数量和有效破片平均速度结果最佳。

由于预制破片成型后，单个破片质量很小，在空气中受到空气阻力影响尤为明显，因此有效破片速度下降较为明显。杀伤爆破弹一般都是近距离伤害目标的，因此可以理解破片弹道为一条直线，破片在空气中受到阻力的运动方程为

vr=v0e-αr

(11)

式中：α为速度衰减系数，本文根据试验环境α取0.05；r为破片距离炸点的飞行距离(m)；vr为破片在r处的飞行速度(m/s)。

将式(10)带入式(11)中得

vr=(684.28+67076.57143x+19.39y-1.31657x2-0.375y2-152xy)e-0.05r

(12)

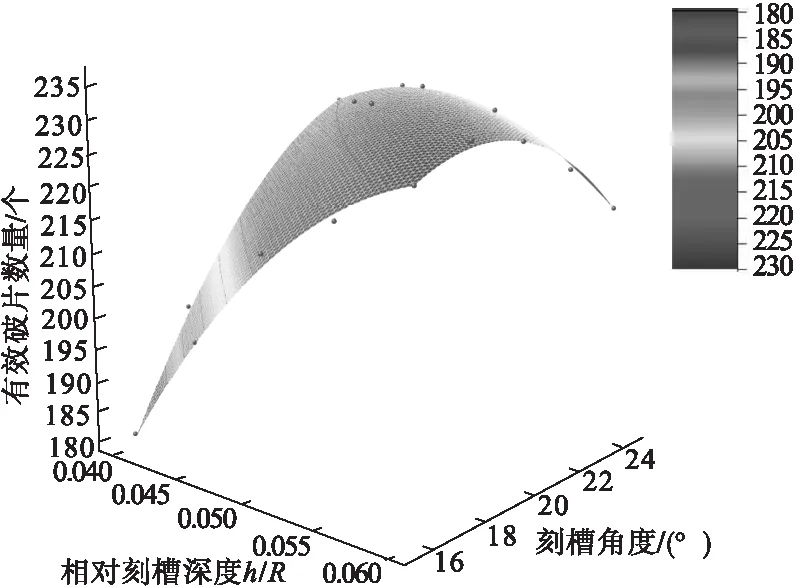
图6 有效破片数量

3 试验验证

对相对刻槽深度为0.05R、刻槽角度为20°，V型槽预控破片杀爆弹的有效破片速度进行2次测速试验，试验测速靶采用梳妆靶，布置为3m、4m、5m、6m。图8、图9为测速试验示意图和现场布置图。

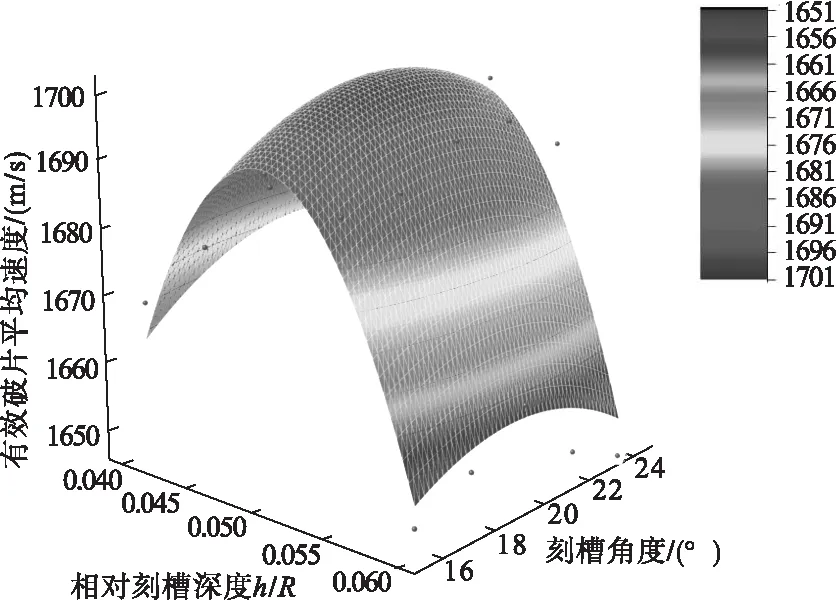
图7 有效破片平均速度

图8 测速试验示意图

图9 现场布置

试验测得预控破片杀爆弹有效破片的平均速度，距离战斗部3m时，有效破片的平均速度约为1495m/s；距离战斗部4m时，有效破片的平均速度约为1411m/s；距离战斗部5m时，有效破片的平均速度约为1343m/s；距离战斗部6m时，有效破片的平均速度约为1270m/s。仿真计算结果计算有效破片平均初速见图7。公式(12)得出距离战斗部3m时，有效破片速度约为1463m/s；距离战斗部4m时，有效破片的平均速度约为1390m/s；距离战斗部5m时，有效破片的平均速度约为1323m/s；距离战斗部6m时，有效破片的平均速度约为1259m/s。速度衰减对比如图10所示，试验测得速度与仿真计算速度趋势相仿，误差率小于5%，二者基本相符。

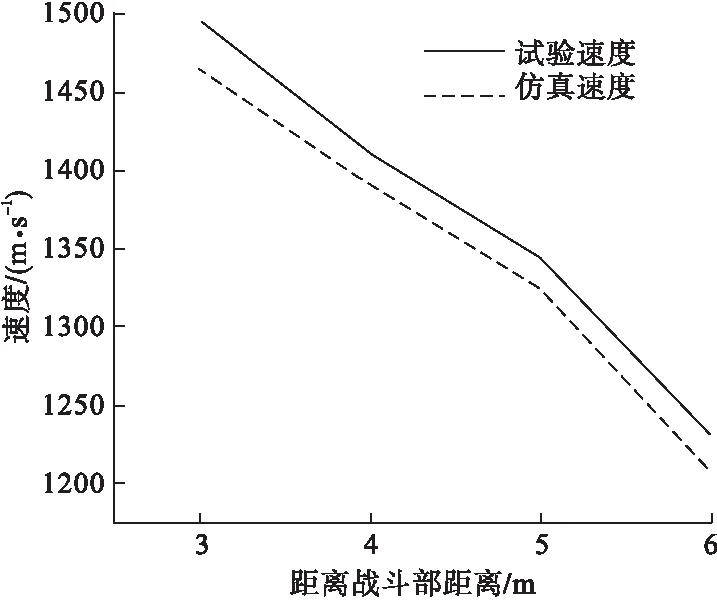
图10 试验和仿真速度衰减对比

对有效破片进行沙爆试验回收，预控破片战斗部平均有效破片数为222个。仿真模拟计算得出有效破片数约231个。试验结果与计算结果的有效破片和自然破片误差率小于5%，爆坑试验中连片破片在沙子的作用下最多连片数明显减小，有效破片个数减少,与仿真计算结果基本相符。

4 结论

对V型刻槽预控破片战斗部进行试验，得到高速有效破片，分析刻槽深度与刻槽角度等参数对成型有效破片数量及速度的影响规律，得到以下结论。

(1) 通过仿真模拟结果，得出刻槽深度与刻槽角度对预控破片沙爆弹战斗部成型及破片的速度的影响规律；当刻槽深度为0.05R，刻槽角度为20°时，成型破片速度和数量最佳；

(2) 通过量纲分析的方法确定有效破片初始速度计算方程和速度衰减方程；

(3) 预控破片战斗部成型的仿真模拟和计算方程与爆坑试验结果对比，成型后的有效破片总数和自然破片总数误差率小于5%，两者基本相符；

(4) 预控破片战斗部成型的仿真模拟和速度衰减方程与测速试验结果对比，成型后破片的初始速度和速度衰减误差率小于5%，两者基本相符。

参考文献：

[1] LI Ying,WU Wei guo,ZHU Haiqing,et al.The Influence of Different Pre-formed Holes on the Dynamic Response of Square Plates under Air-blast Loading[J].Engineering Failure Analysis,2017 (78):122-133.

[2] NING Jianguo,DUAN Yan,XU Xiangzhao,et al.Velocity Characteristics of Fragments from Prismatic Casing under internal Explosive Loading[J].International Journal of Impact Engineering,2017(109):29-38.

[3] Grisaro H,Dancygier A N.Numerical study of velocity distribution of fragments caused by explosion of a cylindrical cased charge[J].International Journal of Impact Engineering,2015(86):1-12.

[4] 蒋浩征.杀伤战斗部破片飞散初速ν0的技术[J].兵工学报,1980,1(1):68-79.

[5] 戴端辉,黄朝会.预控破片弹杀伤面积的技术[J].兵工学报,1998,19(4):365-367.

[6] 郑娜娜,董素荣,王晓蓉,等.高破片率钢预控破片弹毁伤效能分析[J].弹箭与制导学报,2013,33(3):59-62.

[7] 吴成,倪艳光,张渝霞.内刻V形槽半预控破片战斗部壳体的断裂准则[J].北京理工大学学报,2008,28(7):569-572.

[8] 朱桂利,李伟兵,王晓鸣,等.预控破片对厚壁圆管的横向高速冲击作用研究[J].振动与冲击,2016,35(5):115-119.

[9] 印立魁,蒋建伟,门建兵,等.立方体预控破片战斗部破片初速计算模型[J].兵工学报,2014,35(12):1967-1971.

[10] 彭正午,张庆,王晓鸥,等.刻槽参数对预控破片形成情况的影响研究[J].火工品,2013,1:17-20.

[11] 赵凯,高光发,王肖钧.柱壳结果坑冲击性能量纲分析与数值模拟研究[J].振动与冲击,2014,33(11):12-16.

[12] 宋梅丽,李文彬,王晓鸣,等.弹体高速侵彻效率的实验和量纲分析[J].爆炸与冲击,2016,36(6):752-758.

[13] 李丽萍,孔德仁,王芳,等.基于量纲分析的爆炸冲击波效应靶模型分析与实验研究[J].振动与冲击,2016,35(6):100-103.

[14] 王朝成,任辉启,穆朝民,等.一端开口圆筒形爆室线状装药爆炸冲击波峰值压力计算分析[J].振动与冲击,2014,33(9):122-125.

[15] 相升海,徐文龙,张健,等.刻槽式MEFP的成形及侵彻钢靶模式[J].爆炸与冲击,2015,35(1):135-139.