基于CART模型的不纯度函数在不同数据类型中的分类

曹桃云

（广州科技贸易职业学院 公教部，广州 510442）

1 问题的提出

由Breiman等（1984）[1]提出的分类回归树（CART）模型，通过对预测变量X进行分裂，递归拆分预测变量所在的空间，以达到增加反馈变量Y在每一个预测子空间的同质性。通过递归拆分建立的分类回归树具有直观的图形展示、有效处理缺失数据、自动的变量选择和容易解释等特点，因而被广泛地应用于生物学、医学、经济学、金融学以及社会学等众多学科领域中。作为一种重要的非参数统计方法，由于不需要对反馈变量Y进行任何分布或特定关系的假设，分类回归树得到了广泛深入的研究和应用，并发展成为探索复杂数据结构中最灵活、直观和强有力的数据分析工具之一。

基于CART模型的组合方法随机森林[2]和bagging[3]的出现克服了单棵树模型的局限性：（1）树结构受微小数据的扰动变化大；（2）单棵树不足以挖掘数据中蕴含的丰富信息；尤其在预测变量X的维数高，样本量小的情形下，组合方法的优势凸显。在损失了树模型部分解释性的前提下，组合方法大大提高了模型的预测能力。随机森林作为bagging方法的特例，具备的随机抽样和随机选取分裂变量的候选值，树模型之间的独立性进一步增强，使得树模型能从不同的角度刻画数据，泛化误差的上界缩小。本文对基于树模型的不纯度函数在各种数据类型中的发展研究进行了系统的梳理总结，以进一步发展树模型，为数据分析和数据挖掘提供统一可行的非参数方法。

2 不纯度函数在反馈向量不同数据类型中的分类

树是由节点组成的，节点的性质决定了树的性质，同质性高的节点，分类树的效果就理想。图1展示了树结构与预测变量子空间的对应图：x1'x13分别表示年龄和饮酒量，圆圈和黑点表示两种不同的结果。

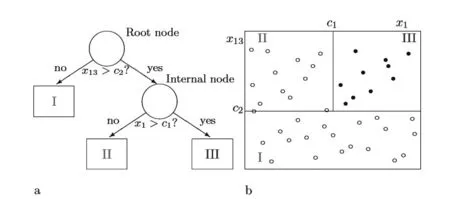
图1 树结构展示图[4]

不纯度函数是用来衡量节点同质性的指标，以Y={0'1}为例，不纯度函数i(τ)是p(Y =1|τ)的非负函数，这里的τ表示节点（以下均代表此含义）。直观的，如果不纯度函数i(τ)=0意味着节点内只有一种结果；如果意味着从节点内随机抽取样本，等可能的得到0'1两种结果。因此，i(τ)是树模型中的重要指标。

给定观测数据N个样本，p是预测向量X的维数，m是反馈向量Y的维数。下面从m=1、m≥2及Y的类型：离散型、连续型及关联数据类型等对不纯度函数进行分类研究。

2.1 反馈向量Y是离散型时的广义熵

m=1且Y={0'1}，分类树和随机森林是常用的分析这类数据的树模型方法，不纯度函数：i(τ)=-plnp-(1-表示在节点τ的条件概率，即Y=1的条件概率，1-p=p(Y =0|τ)表示在节点τ的条件概率即Y=0的条件概率，p(Y)表示随机变量Y等于0或1的概率表示函数的期望。m=1且Y={c1'…'ck}，这里的c1'…'ck为节点τ内的k个类（k≥2），分类树和随机森林是常用的分析这类数据的树模型方法，不纯度函数为τ内第cj个类的条件概

率，p(Y)表示随机变量Y等于c1'…'ck中某个类的概率，表示函数的期望。

m=2且Yij={0'1}，这里的i、j分别表示第i个样本和Y的维数，Zhang[5]最早提出基于树模型分析这类数据的广义熵不纯度函数其中̂是联合概率分布中参数向量ψ'θ的极大似然估计表示参数向量ψ极大似然估计的转置表示正则化常数。

对于m≥2且Yij={c1'…'ck}的数据，可以转化为m=1且Y={0'1}的数据类型[4]。

2.2 反馈向量Y是连续型时的广义基尼均值差

m=1且Y是连续型时，分析这类数据常用的非参数方法有回归树和随机森林，不纯度函数yˉ(τ))2，m 和 yˉ(τ)分别表示 τ的样本和 τ内反馈变量 y 的样本均值。

m≥2且Y是连续型时，分析这类数据可以选用的非参数方法有多元回归树[6，7]和基于E-距离的多元bagging[8]，其中文献[8]中的不纯度函数广义基尼均值差具有更广泛的意义表示τ内的样本数，‖·‖表示欧几里得范数，α∈(0'2)，特别注意的是Ym'Yj都是向量。当m退化为1时，广义基尼均值差和m=1时的不纯度函数是等价的[8]；当m≥2时，广义基尼均值差和多元回归树中的距离均值的平方和是等价的[8]。

2.3 反馈向量Y是其他情形

（1）纵向数据

纵向数据是一类特殊的数据类型，是指一系列试验个体随着时间的演变进行跟踪测量得到的数据，出现在生物学、医学、社会学等众多领域中。观测到的数据为：(yij' xij'tij)'j=1'…'mi,i=1'…'n，这里的i表示第i个样本，j表示第 j次观测，是和样本i有关的，反馈变量yij是在时间tij观测到的。图2展示了纵向数据的特点。

图2中的左图表示所有观测值的阅读能力散点图，右图表示跟踪每个个体两个不同年龄的阅读能力图，随着年龄的增长，阅读能力呈现明显上升的趋势。

由于反馈变量之间的特殊关联性，使得纵向数据分析成为数据分析中的难点问题。Segal(1992)[10]首次提出运用树模型对纵向数据进行分析。不纯度函数这里的 θτ是依赖于 τ的参数向量，ψ(θτ)是节点 τ内的协方差矩阵，ψ-1(θτ)表示协方差矩阵的逆矩阵。Loh等（2013）[11]提出卡方检验挑选分裂变量的树模型方法，适用于随机时间点的纵向数据分析。

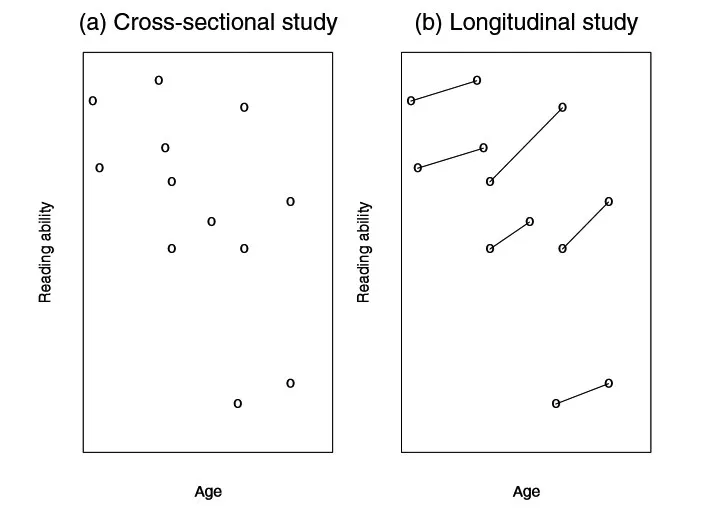
图2 阅读能力对比图[9]

（2）删失数据

删失数据是生存分析中常见的数据类型，是指由于种种原因，所采集的数据中许多应该采集而未能采集，应提交而未在一些时点上提交造成的数据不完全。生存树是分析此类数据的树模型方法。其中的不纯度函数i(τ)=这里的 Sτ代表 τ的Kaplan-Meier曲线⋅表示三种可能的同质性节点和Sτ最好的匹配，dp(')是两种生存函数之间的一种离散度量，设F1和F2是两个分布函数min{t:Fi(t)≥u}，i=1'2。

基于对数秩的随机生存森林的出现，提高了生存树的预测能力。和其他方法相比，随着噪音变量的增加随机生存森林具有明显的预测优势，但会受到删失率的限制。

（3）反馈变量Y={0'1}的医疗数据类型

精准医疗中，观测数据这里的 Ti表示第i个样本的治疗方案，第i个样本的反馈变量Yi={0'1}，Yi=1表示在治疗方案下病情出现好转，第i个样本的预测向量 Xi={Xi1'Xi2'…'Xip}，Tsai等（2016）[12]首次提出修改分类树方法分析精准医疗数据，以最大化两种治疗方案结果差的平方作为树模型中τ的度量函数[12]DIFF(τ)=(p (Y=1|T=A'τ)-p(Y =1|T=B'(τ))2，这里的T)=A'B表示两种治疗，如A药或B药，p Y=1|T=A'τ'p(Y =1|T=B'τ)分别表示节点τ中的样本在A、B药作用下，病人病情好转的条件概率。条件概率差的平方越大，意味着两种治疗的结果出现较大的差异，有利于病人选择最适合自己的医疗方案，达到精准医疗的目的。

3 总结

作为一种非参数统计方法，基于分类回归树模型，一直获得广泛应用并被拓展到各种数据类型中。不纯度函数在树模型的生成过程中起着重要作用。本文通过对不同数据类型的梳理，将不纯度函数归为：广义熵（反馈向量Y是离散型时）、广义基尼均值差（反馈向量Y是连续型时）、最小二乘度量（纵向数据）、度量函数DIFF()τ（精准医疗应用）等，以期对不纯度函数在树模型的实证应用中提供参考。

[1]Breiman L,Friedman J,Stone C,Olshen R.Classification and Regression Trees[M].New York：CRC Press，1984.

[2]Breiman.Random Forests[J].Machine Learning,2001,(45).

[3]Breiman L.Bagging Predictors[J].Machine Learning,1996,(24).

[4]Zhang H,Burton H.Recursive Partitioning and Applications[M].New York:Springer,2010.

[5]Zhang H P.Classification Trees for Multiple Binary Responses[J].JASA,1998,(93).

[6]Glenn De’Ath.Multivariate Regression Trees:A New Technique for Modeling Speciesenvironment Relationships[J].Ecology，2002,(83).

[7]Larsen D R,Speckman P L.Multivariate Regression Trees for Analysis of Abundance Data[J].Biometrics，2004,(60).

[8]Cao T Y，Wang X Q，Zhang H P.Energy Bagging Tree[J].Statistics and Its Interface,2016,(9).

[9]Peter X，Song K.Correlated Data Analysis:Modeling,Analytics,and Applications[M].Canada：Springer,2007.

[10]Segal M R.Tree-Structured Methods for Longitudinal Data[J].JASA,1992,(87).

[11]Loh W Y,Zheng W,et al.Regression trees for Longitudinal and Multiresponse Data[J].The Annals of Applied Statistics,2013,(7).

[12]Tsai W M,Zhang H P，et.al.A Modified Classification Tree Method for Personalized Medicine Decisions[J].Statistics and its interface,2016,(9).