定数截尾情形下Poisson-Lomax分布的Bayes估计

张春雨，刘禄勤

（武汉大学 数学与统计学院，武汉 430072）

1 问题的提出

随着寿命分布理论的深入发展与广泛应用，各种新型的寿命分布被相继提出。Admidis和Loukas（1998）[1]对指数分布与几何分布进行复合，得到的新分布称为Exponential-Geometric 分布；Kus（2007）[2]通过复合指数分布与Poisson分布得到了Exponential-Poisson分布；Hemmati（2011）[3]将Weibull分布与Poisson分布进行复合，提出了Weibull-Poisson 分布；Alzahrani（2014）[4]采用相同的机制对Lomax分布和Poisson分布进行复合，得到的分布称为Poisson-Lomax分布。这些文献研究了所得新分布的性质，并给出了参数在完全样本下的极大似然估计。

然而在寿命试验中，受试验时间、费用等因素的限制，取得完全样本往往有较大难度。例如，在医学药物试验中，受试者迁居外地而失去观察，对药物有不良反应从而退出试验；受试验时间、费用的限制，无法将试验进行到所有元件都失效等。在这些情形下，只能得到一组不完全样本。定数截尾是数据缺失的一种基本类型，王德辉（1999）[5]研究了定数截尾情形在熵损失函数下指数分布参数的Bayes估计，徐凌云（2010）[6]、鄢伟安（2012）[7]等给出了定数截尾情形下Exponential-Poisson分布参数的Bayes估计，并对不同损失函数下的估计进行了比较。对于上述新分布，定数截尾情形下的参数估计研究尚不全面。本文研究定数截尾情形下Poisson-Lomax分布的参数估计。

在可靠性和寿命试验研究中，Lomax分布是一种使用广泛的寿命分布。该分布包含了单调递增和单调递减的失效率，被广泛应用于分析医学、生物科学和工程科学等方面的寿命试验数据处理中。Poisson-Lomax分布是2014年由Alzahrani[4]新提出的一种三参数寿命分布，是Lomax分布的推广。

设Y1' Y2' …' Yn独立同分布于参数为α' β的Lomax分布，其密度函数为：

其中 α' β＞0。Z 服从参数为 λ∈(0'M)' 0＜M≤∞ 的截零Poisson分布，即：

且 Z与{Yk:k≥1}独立。令ξ=max{Y1'Y2'…'YZ}，则称 ξ服从参数为 (α' β' λ)的Poisson-Lomax分布。其分布函数为：

密度函数为：

其中α'β'λ＞0。该分布的危险率函数为：

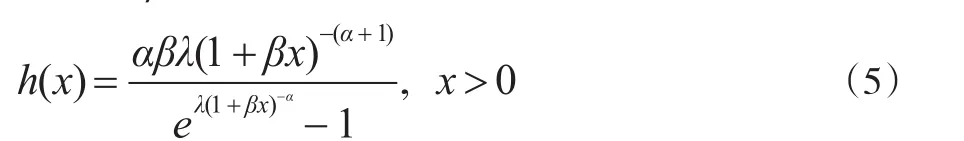
随参数的不同取值，危险率函数h(x)具有单调减和单峰两种形态，其灵活的危险率函数给统计建模带来了更多的选择。文献[4]分析了该分布的密度函数与危险率函数，给出了各阶矩与顺序统计量，以及完全样本情形下参数的极大似然估计与区间估计，并将此新分布应用于实际数据。该分布在实际场景中的良好效果展示了其良好的应用前景。本文将给出定数截尾情形下Poisson-Lomax分布参数的Bayes估计，并进行数值模拟。模拟结果表明，在数据量较小时，Bayes估计优于极大似然估计。

2 参数的Bayes估计

在寿命试验中，假定n个试验对象的寿命独立同分布，规定进行到有r个试验对象失效时试验终止。设此r个试验对象的生存时间依次为x1'x2'…'xr,则x1≤x2≤…≤xr。记x=(x1'x2'…'xr),由文献[8]可知，x的联合分布密度为：故似然函数为：

先考虑 α、β已知时参数 λ的Bayes估计。记ti=(1+βxi)-α，则式（7）可记为：

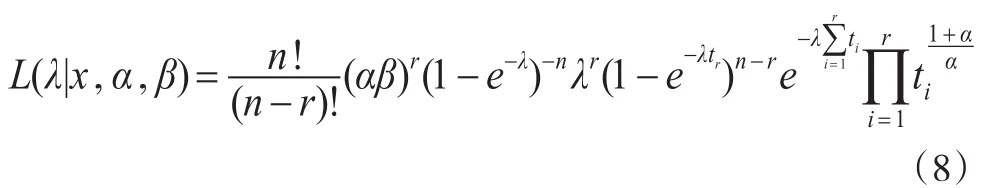
取λ的先验密度为广义均匀分布：

其中0＜M≤∞，则λ的Bayes后验密度为：

记为决策函数的后验风险为的损失函数，则：

λ 的Bayes估计的定义为

损失函数是影响Bayes估计效果的因素之一，Linex损失函数和刻度平方损失函数是常用的两种损失函数。刻度平方损失函数由于计算方便，在参数估计问题中应用广泛[9-11]。Linex损失函数由Varian于1975年提出，Zellner（1986）[12]将Linex损失函数用于Bayes统计推断问题，其后Linex损失函数日渐成为Bayes估计中常用损失函数之一。

本文将损失函数取为Linex损失函数和刻度平方损失函数，分别求参数的Bayes估计。

2.1 参数λ在Linex损失函数下的Bayes估计

对 λ̂= λ̂(x),Linex损失函数的定义为：

引理 1：记为 λ在损失函数式（12）下的Bayes估计,则：

证明：对式（12）求条件期望，得：

等式两端对λ̂求一阶偏导得：

令可得又：

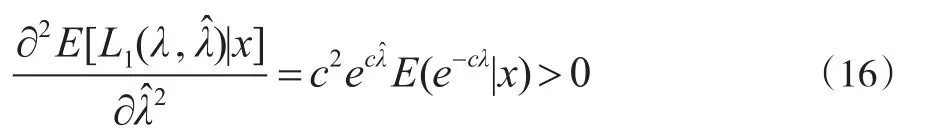
故作为 λ在损失函数式（12）下的估计是唯一的。

定理1：对于先验分布式（9）,在损失函数式（12）下参数λ的Bayes估计为：

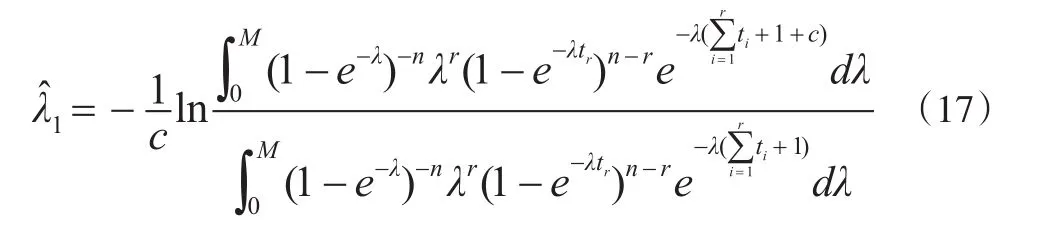
证明：由式（10）及引理1，可得：

定理得证。

2.2 参数λ在刻度平方损失函数下的Bayes估计

对刻度平方损失函数定义为：

特别地，当 k=0 时为平方损失函数。

引理 2：记为 λ在损失函数式（19）下的Bayes估计，则：

证明：对式（19）两端求条件期望，得：

等式两端对λ̂求一阶偏导得：

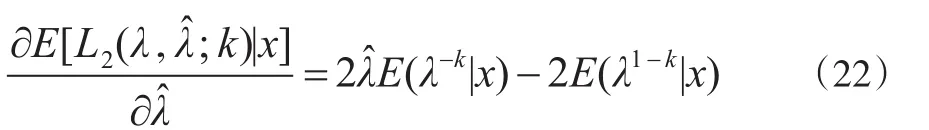
令可得又：

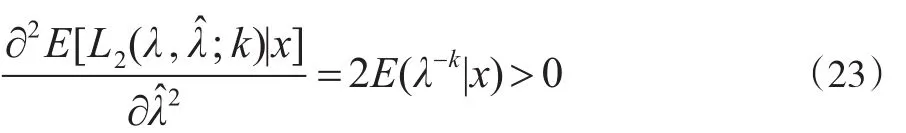
故作为λ在刻度平方损失函数式（19）下的估计是唯一的。

定理2：对于先验分布式（9）,在损失函数式（19）下参数λ的Bayes估计为：

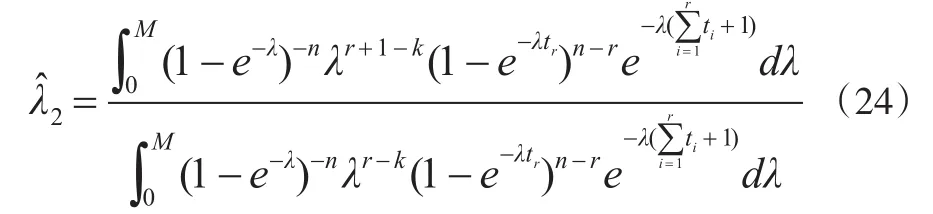
证明：由式（10）及引理2，可得：

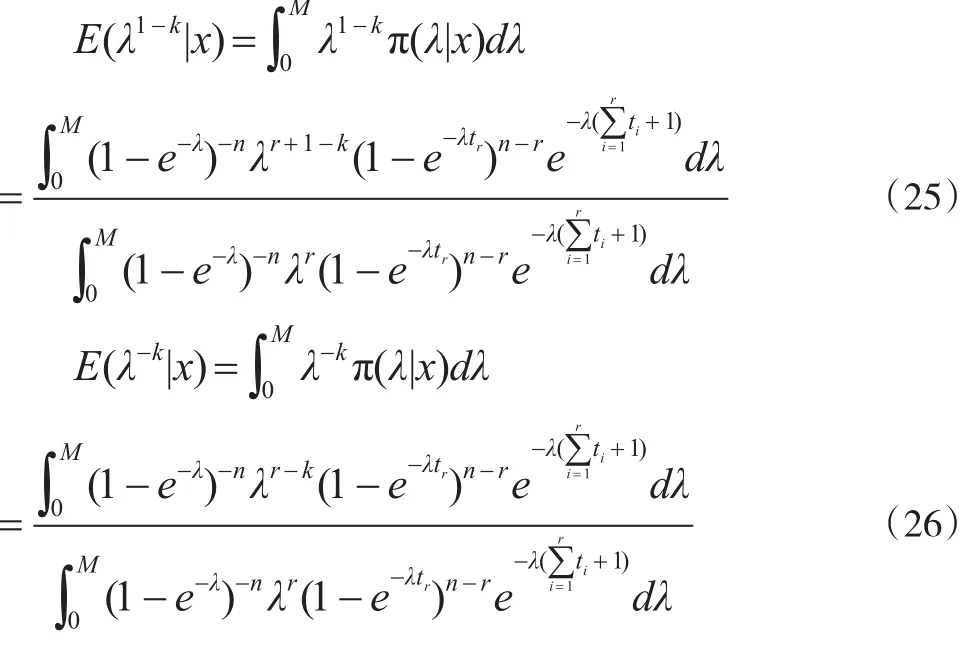
由式（20）、式（25）、式（26），可得式（24）。定理得证。

2.3 参数α 的Bayes估计

类似于上文对参数λ的Bayes估计，本文可以考虑λ、α已知时参数β的Bayes估计和β、λ已知时参数α的Bayes估计。限于篇幅，本文仅给出β、λ已知时参数α的Bayes估计。设 β、λ已知，则由式（7）得：

取α的先验密度为广义均匀分布：

其中0＜M≤∞，则α的Bayes后验密度为：

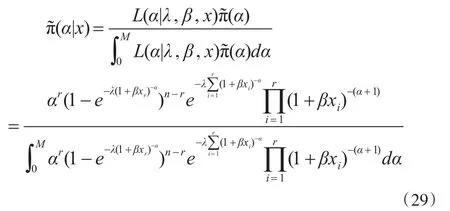
与参数λ的Bayes估计方法类似，本文可以得到α在Linex损失函数下的Bayes估计α̂1与刻度损失函数下的Bayes估计表达式如下：

3 数值模拟

由文献[4]，Poisson-Lomax分布的分位数函数为：

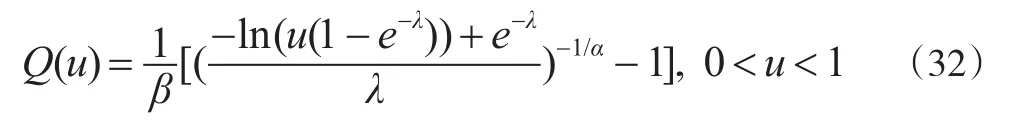
对参数λ的极大似然估计λ̂m及在两种损失函数下的Bayes估计 λ̂1、λ̂2进行数值模拟。步骤如下：

（1）确定需要产生的样本容量n,以及截尾数r；

（2）固定 α=2,β=0.5,对 λ'M'n'r分别取不同的值，进行后续步骤；

（3）产生独立的U1'…'Un～ Unif(0,1),令 X1=Q(U1)'…'Xn=Q(Un),则 X1'…'Xn～F(x;2'0.5'λ)。取 x1=X(1)'…'xr=X(r),计算 ti=(1+βxi)-α'i=1'…'r；

（4）计算记e-zc′,对 M ＜ ∞ ,由大数定律：

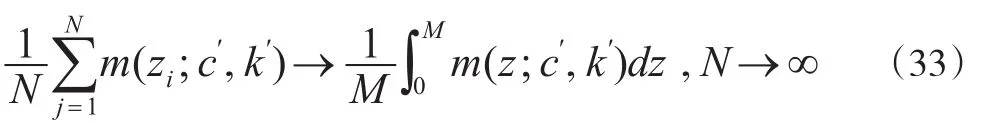
其中，z1'…'zN～Unif(0'M)。取 N=10000'c=0.01'k=0,计算

在λ取值范围为λ∈(0'∞)时，有：

其中，z1'…'zN～Exp(1)。取 N=10000'c=0.01'k=0,计算

（5）对每个 λ的取值，重复步骤（3）、步骤（4）1000次，并求其均值、标准误、均方误差。

设 λ̂m为 λ的极大似然估计，即 λ̂m为在 α、β 已知时似然函数式（7）的最大值点，用Newton法求 λ̂m，迭代终止条件为两次结果相差小于0.001。将两个Bayes估计与极大似然估计进行比较。

由以上模拟步骤，可得如下页表1所示模拟结果。表1展示了λ=5、M=∞时，在不同的n、r取值下λ的估计。由表1可以看出，估计的准确度随n、r的增加而上升。当n不变而r增大时，准确度提高；当r不变只有n增加时，准确度同样会提高。由表1易见，此时极大似然估计优于Bayes估计。

表2（见下页）比较了在M 取有限值时两种估计的效果。取λ=4、M=100,n、r取值如表2所示。当数据缺失较多，即r较小时，极大似然估计效果较差。表2显示，r=2、r=5时，n的三种取值情形下Bayes估计均优于极大似然估计；当观察到的数据较多，即有效样本量r=20时，极大似然估计效果更好。同时，不难发现当观察到的数据很少即r=2或r=5时，表2中由左至右Bayes估计相对极大似然估计的优势越来越明显。这是因为由左至右n增大，数据缺失程度变大，极大似然估计因此效果变差。

表1 λ=5、M=∞时估计结果比较

表2 λ=4、M=100时模拟结果

表3给出了不同M取值对Bayes估计准确程度的影响。由表3可知，M=∞时Bayes估计效果最差，M=50时估计效果最好，M=100时估计效果比M=50时略差。此处M的取值在Bayes估计中决定了λ的先验分布，M取值较小，给出的先验信息更充分，估计更准确。

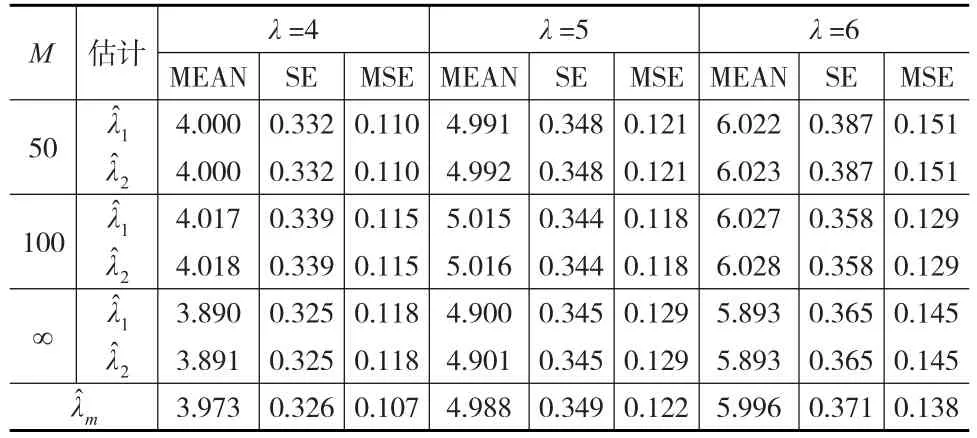
表3 n=1000、r=20时模拟结果

类似地，本文对参数α的两个Bayes估计进行模拟。取c=0.8、 k=2，得到表4所示结果。由表4可知，除数据量较小的n=60、r=10情形，M取值对α估计准确度影响不大，因此在数据量较大时，对α的估计可取先验分布为(0'∞)上的广义均匀分布。

表4 α=5时模拟结果

综上，可得如下结论：（1）当r很小时，Bayes估计明显优于极大似然估计；（2）r固定时，n越大，数据缺失程度越大，Bayes估计相对极大似然估计的优势越明显；（3）对参数λ而言，M取值越小估计越准确；（4）对参数α，当数据量较小时M取有限值估计更准确，数据量较大时M取值对估计准确度影响相对较小。

[1]Adamidis K,Loukas S.A Lifetime Distribution With Decreasing Failure Rate[J].Statistics and Probability Letters,1998，39(1).

[2]Kus C.A New Lifetime Distribution[J].Comput.Stat.Data Anal,2007,51(9).

[3]Hemmati F,Khorram E,Rezakhah S.A New Three-parameter Ageing Distribution[J].Journal of Statistical Planning and Inference,2011,141(7).

[4]AlZahrani B，Sagor H.The Poisson-Lomax Distribution[J].Revista Colombiana de Estadística,2014,37(1).

[5]王德辉,宋立新.熵损失函数下定数截尾情形参数的Bayes估计——指数分布情形[J].应用概率统计，1999,15(2).

[6]徐凌云,朱宁,方爱秋,唐清干.定数截尾情形指数-泊松分布参数的Bayes估计[J].统计与决策,2010,(15).

[7]鄢伟安,师义民,刘英.不同损失函数下指数-泊松分布的Bayes估计[J].火力与指挥控制,2012，37(2).

[8]曹晋华,程侃.可靠性数学引论[M].北京：高等教育出版社,2012.

[9]陈家鑫.AR模型阶数依平方损失函数下的Bayes估计[J].应用概率统计,1991,(2).

[10]宋立新，陈永胜，许俊美.刻度平方误差损失下Poisson分布参数的Bayes估计[J].兰州理工大学学报,2008,(5).

[11]彭家龙，李顺波.刻度平方误差损失下二项分布无失效数据的可靠性分析[J].佳木斯大学学报：自然科学版,2009,(1).

[12]Zellner A.Bayesian Estimation and Prediction Using Asymmetric Loss Function[J].Journal of the Americcan Statistical Assication,1986,81(394).