基于特征选择与SVM的质量异常模式识别

刘玉敏，赵哲耘

（郑州大学 商学院，郑州 450001）

0 引言

随着工业物联网的兴起，现代化工厂安装了大量的信息传感设备，这使得实时采集能有效反映生产和加工过程运行状态的数据流，进而实现质量监控成为现实。这些数据流总体反映了连续生产过程的运行状态，而其运行状态直接影响产品质量的优劣。由于过程中受到人、机、料、法、环、测等因素的影响，动态过程质量模式可分为正常模式和异常模式两大类。当动态数据流呈现出质量异常模式时，通常表明机器设备存在潜在问题，需要作出调整。因此，对数据流进行降维，并建立高效的异常监控模型，成为了质量监控的核心问题[1]。

目前，对于过程质量异常监控方法的研究多围绕基于特征提取的质量异常模式识别展开，其中应用的特征主要有时域特征[2]、形状特征[3]、小波分解特征[4]等。例如，Hassan[5]提取了原始数据的6种时域特征，该特征具有维度低、表征能力强的特点；Ranaee等[6]将形状特征与时域特征进行混合，利用支持向量机对6种质量模式进行了有效的识别。刘玉敏[7]使用一维离散小波分解近似系数同小波重构序列的4个形状特征进行混合。综上所述，当前特征提取的方法主要是通过单一数据特征或混合。然而，研究表明，单一种类特征对于原始数据描述能力有限，而高维混合特征会提高模型的复杂度进而降低其识别效率。因此，如何提取维度低并包含丰富信息的特征，并构建与分类任务复杂度相匹配的高精度识别模型成为了动态过程质量异常模式识别的关键。本文提出了一种基于特征选择的混合特征集与支持向量机相结合的动态过程质量异常模式识别方法。

1 质量异常模式分类

在动态过程中，由于受到不同因素的影响，其质量特性数据流也呈现不同的波动模式。其中，随机因素影响下的质量特性数据流在目标值上下随机游走，在动态过程中属于正常模式。当质量特性数据流波动呈现趋势、阶跃和周期等状态时，表明过程受到异常因素的影响，此刻处于异常状态[8]，如图1所示。

2 基于特征选择的质量异常模式识别模型

2.1 一维离散小波分解

虽然动态过程产生的原始数据流能够较为全面地反映动态过程运行状态，但由于高噪声、高维度等特点，若将

其直接应用于分类任务中会造成较低的识别精度和识别效率。为对数据流的整体和局部变化特征进行提取和增强，使用一维离散小波分解（Discrete Wavelet Transform,DWT）将原始数据流转化为高频细节部分和低频近似部分，经过L层变换后，过程数据流的整体变化趋势信息被分解到了最后一层的低频近似系数中，而其噪声被分解在各层的高频系数中[9]。记P0X=X，通过正交投影PjX和QjX将j-1层的小波近似系数Pj-1X分解为：

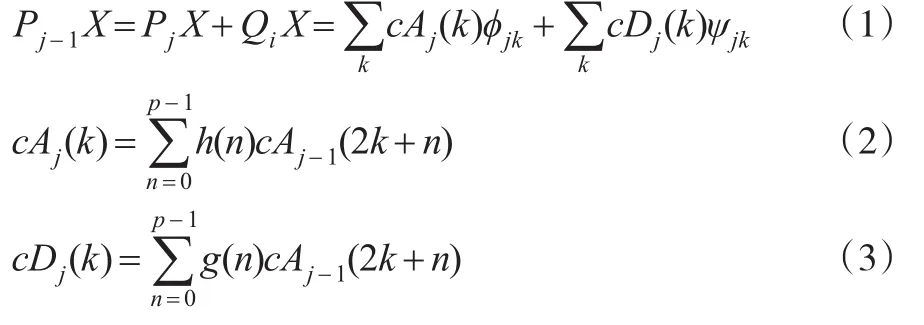
式（1）至式（3）中，h(n)和g(h)分别为低通、高通滤波器的脉冲响应，p为权系数的长度。cAj和cDj分别为数据流在j层小波分解中的低频近似系数和高频细节系数；j=1,2,3,...,L,L=0,1,2,...,N/2j-1，N为原始数据流长度，j为最大分解层数；φ(t)和ψ(t)分别为定标函数与子波函数。中点坐标为

2.2 质量异常模式的形状特征与时域特征

不同的动态过程质量模式都存在其独特几何形状。形状特征是在通过对原始数据进行变换或计算而得到的能有效表达各个质量异常模式的数字量。本文采用以下几种形状特征参与特征选择[10]：

（1）对模式序列不作分段提取，可以得到SB和PSMLSC特征：

式中，N为模式数据序列长度；ti为第i个数据点到原点的距离；yi为第 i个采样点的采样值

（2）将模式序列进行固定分段，可得到SRANGE和REAE特征：

式中，sjk为模式序列的第j段与第k中点连线的斜率，每段对应的n1取值分别为1、16、31、46；MSE为整个模式序列的最小二乘估计的均方误差值，MSEjk为将第j段与第k段数据点重组后所得到的序列的最小二乘估计的误差值。

（3）对模式序列做不固定分割，其中分割后的两段数据序列的最小二乘估计的合并均方误差（PMSE）的最小值点为分割点，可以得到ABDPE特征：

式中，B为整个序列的最小二乘拟合直线的斜率，Bj（j=1,2）分别为分割后的两段序列的最小二乘拟合直线斜率。

现有的研究表明，时域特征能够刻画样本数据的基本特征，并能有效地对质量异常模式进行区分，本文选取了均方幅值、标准差、峰值、方根幅值、平均值、峭度和最大值7个特征来识别质量异常模式，具体公式见表1。

表1 时域特征

2.3 一种基于分类精度的序列前向选择方法

序列前向选择方法（Sequential Forward Selection，SFS）是一种启发式搜索方法，先把目标特征集定义为空集，按照特征评估函数，加入使其最大的一个特征，最后得到达到要求的特征子集。相比序列前向选择方法，广义序列前向选择方法是根据特征评估函数向现有特征集中加入r个特征，使得特征评估函数达到最大值从而得到满足要求的特征子集。基于分类精度的序列前向选择方法[11]（sequential forward selection based on classification accuracy，CA-SFS）是序列前向选择法和广义序列前向选择法的混合，可根据需要来灵活改变r的取值，若添加一个特征对于分类精度没有提高，即可加入2个、3个甚至更多的特征组合，本文为了避免计算过于复杂，在此设定r≤4。本文将低频小波近似系数作为特征选择起点，将分类器的分类精度作为特征评估函数，加入使其分类精度提升最大的特征或特征组合，直到得到满足要求的特征集。基于分类精度的序列前向选择识别过程如图2所示。

图2 基于分类精度的序列前向选择识别过程

2.4 SVM多分类设计

支持向量机（Support Vector Machine，SVM）能够有效地解决小样本下的线性不可分的二分类问题。其原理是通过核函数将线性不可分的数据映射到高维空间寻找最优分类超平面，从而实现低维空间的非线性分类，结构风险最小化原则使得支持向量机较其他分类器具有泛化能力强的特点。其分类原理如下：

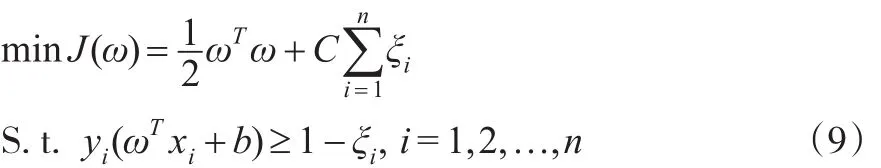
式中，C为惩罚因子，C的大小会对分类器的容错能力产生影响；ξi为松弛变量。使用核函数k（xi,x）替代简单的内积后，可得到SVM的判别函数：

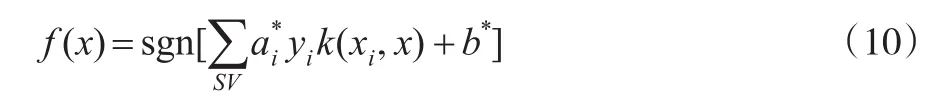
由SVM判别函数可知，单个的SVM仅能解决二分类问题，常用的二分类SVM有一对一、一对多、半对半等。而对于本文的六分类问题，需要多个支持向量机组成联合分类器（MSVM）来实现对于动态过程的六种模式识别。并且，SVM中罚函数和核函数参数的选择直接影响到对于分类误差的宽容度和核映射后的数据分布，进而对其分类精度造成影响。因此，模型参数的选择成为了构建支持向量机分类模型的亟需解决的关键问题[12]。粒子群算法（Particle Swarm Optimization，PSO）是一种基于迭代的优化算法，相较于常见的遗传算法和网格搜索法，具有无需编码、全局寻优能力强、耗时短等优点，且能够避免人工参数选择的主观性和片面性，因此，本文选用PSO算法对支持向量机的参数进行自动寻优，从而提升识别模型的分类精度。图3为本文构建的多分类支持向量机模型。

图3 质量异常模式识别模型

核函数能够将高维空间的内积转化为低维空间的内积，能够在解决线性不可分问题的同时避免“维度灾难”，但核函数的选择仍缺乏理论指导。高斯核函数（Radial Basis Function，RBF）具有较少的核函数参数，具有较低的训练复杂度和较好的分类性能，被广泛用于SVM分类中。因此，本文选用RBF核函数来实现支持向量机分类器的非线性分类（RBF-SVM），公式如下：

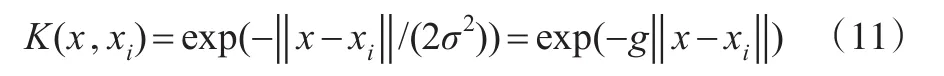
3 仿真实验设计

3.1 样本数据生成及参数设置

由于实际生产过程中的异常数据难以批量获取，且大都需要破坏性试验来扩充异常样本量，其成本较高、实用性较差。因此本文采用蒙特卡洛（Monte Carlo，MC）方法生成所需要的正常和异常样本数据：

x(t)=μ+γ×σ+d(t)'t=1'2'…'n

式中，μ为设计目标值；σ为过程能力标准差；γ为随机因素造成的波动服从高斯白噪声，过程固有，无法去除或去除成本较高；d(t)为异常因素导致的波动，可查明原因并消除。每种模式的仿真公式见表2。

表2 Monte Carlo仿真公式

3.2 数据特征提取

利用蒙特卡洛法生成仿真数据，其中对每种质量模式生成120组仿真样本，其中随机抽取20个为训练样本，共计120组测试样本，其余600组为测试集，每组样本均包含连续60个质量特性观测点。首先，针对阶跃模式与趋势模式识别率整体较低的特点，对原始数据进行一维离散小波分解，采用Db4母小波函数对数据流进行尺度为3的一维离散小波分解，得到一个低频近似系数和三个高频细节系数。观察表明，第三层低频近似系数cA3有效去除了原始数据中的噪声信号，保留了动态数据流的整体变化特征。

表3 特征选择实验过程

表3为特征选择的实验过程，从中可以看出，在第一轮的特征选择中，将全部的12个形状特征作为备选，分别依次参与小波特征的混合。从表3可看出，本文特征选择中使用了四次SFS方法和两次GSFS方法。因此本文选择的特征集合为：小波特征集、峭度、最大值、ABDPE、SB、峰值、SRANGE、均方幅值和均值。相比12个特征全部混合，本文选择出来的特征与小波特征混合使得识别精度有了显著提高。选取的混合特征向量为：

Zbest=[cA3峭度最大值ABDPE SB峰值SRANGE均方幅值均值]

3.3 最优特征集下的SVM训练及参数优化结果

本实验基于Matlab2014b和Libsvm工具箱，并对核函数参数g，罚函数c,加速常数c1和c2初始化参数值进行设定。本文模型PSO算法参数设定、识别精度及参数见表4。

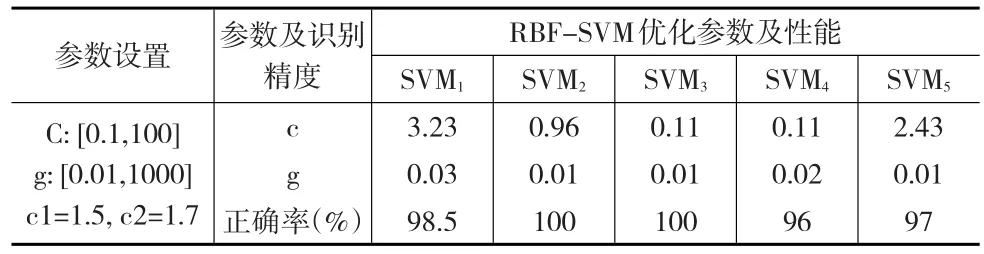
表4 RBF-SVM参数优化结果

3.4 实验结果分析

（1）实验一：一般SFS方法和本文所用的CA-SFS方法的识别精度对比

本实验对比了SFS方法和本文方法所选取的混合特征集，所选取的特征集和对应的分类效果如图4和图5所示。两图横轴的特征为本次特征选择中分类精度最高的特征组合维数，从图4中可看出，当使用SFS方法时，精度在97%上下波动，而第22维识别精度最高达到97.17%。图5为本文选择的CA-SFS方法，本方法是通过将SFS和GSFS方法相结合来寻找目标特征集。本方法所选择的22维最优混合特征集的识别精度达到了98.3%。实验表明，本文选择的方法优于SFS方法，在相同特征维数下，有效地提高了对于质量异常模式的总体识别率。

图4 SFS方法选择不同数目特征集的分类准确性

图5 本文所提方法选择特征集的分类准确性

（2）实验二：基于不同特征的质量模式识别精度对比

为验证本文所选择特征的有效性，本实验对比了原始特征、小波形状混合特征、小波时域混合特征、小波时域形状混合特征（多特征）和本文所提方法得到的混合特征作为PSO-SVM的输入进行质量异常模式识别的效果。实验结果如表5所示。

从表4的识别结果进行对比后可知：

（1）本文选择的特征能在较大程度上兼顾特征维数和分类器的分类效率，但如何改善对于正常模式的识别精度，还需要进一步改进特征集的表达能力和识别方法，从而提高模型对于质量异常模式的识别精度。

（2）单一种类特征（7维时域特征、5维形状特征）与小波特征混合所取得的识别精度相比多特征混合较低。这是因为单一种类的特征使得对质量模式表达能力有限。本文所提方法能够在整体变化特征的完整性的基础上剔除时域特征和形状特征中多余的信息，提高了模型的识别精度并兼顾其计算效率。

（3）本文得到的最优特征相对于多特征混合具有较高的识别精度，这是因为在质量异常模式识别中，并不是特征的维数越高识别精度越高，过多的特征具有较多的冗余和噪声；虽然较低的特征维数具有训练复杂度低等优点，但较少的特征会造成质量异常模式的信息缺失，使得对各模式的识别精度和表达能力有限。

表5 识别结果

4 结束语

本文在综合分析已有特征选择方法的基础上，从5维形状特征和7维时域特征中选择出9个特征与小波低频近似系数进行混合作为模式分类特征，以粒子群算法进行参数寻优过的支持向量机作为分类器。低频系数能够凸显质量模式的整体变化趋势，形状特征和时域特征能够强化数据的局部特性，理论分析和仿真实验表明，本文所提方法通过选择后的特征向量与小波低频系数进行混合，删除不必要的特征，保留能提升识别性能的特征集合，提高了分类器的效率和识别精度。但质量异常模式识别中，哪些特征能够对质量异常模式做出较为完备的表达、如何较少小波分解造成的信息缺失，还需要进一步研究。

[1]刘玉敏,周昊飞.动态过程质量异常模式ANN-SVM识别模型及仿真分析[J].统计与决策，2016,(9).

[2]Petros X,Talayeh R.A Weighted Support Vector Machine Method for Control Chart Pattern Recognition[J].Computer&Industrial Engineering,2014,(70).

[3]Gauri S K,Chakraborty S.Feature-based Recognition of Control Chart Patterns[J].Computer&Industrial Engineering,2006,(51).

[4]吴长坤,赵丽萍.基于小波分析和SVM的控制图模式识别[J].中国机械工程，2010,21(13).

[5]Hassan A,Shariff M.Improved SPC Chart Pattern Recognition Using Statistical Features[J].International Journal of Production Research,2003,41(7).

[6]Ranaee V,Ebrahimzadeh A.Application of the PSO-SVM Model for Recognition of Control Chart Patterns[J].ISA Transaction,2010,49(4).

[7]刘玉敏,周昊飞.基于多特征混合与支持向量机的动态过程异常监控[J].计算机集成制造系统,2015,21(10).

[8]刘玉敏,周昊飞.基于小波重构与SVM-BPNN的动态过程在线智能监控[J].系统工程理论与实践,2016,36(7).

[9]刘玉敏,赵哲耘.基于多特征与MSVM的动态过程异常监控[J].组合机床与自动化加工技术,2017,(2).

[10]宋李俊,赵虎.基于融合特征与支持向量机的控制图模式识别[J].计算机应用研究,2014,31(3).

[11]易超群,李建平,朱成文.一种基于分类精度的特征选择支持向量机[J].山东大学学报：理学版,2010,45(7).

[12]张敏,程文明.基于自适应粒子群算法和支持向量机的控制图模式识别[J].工业工程,2012,15(5).