Fe掺杂GaN光电特性的第一性原理研究∗

贾婉丽 周淼 王馨梅 纪卫莉

(西安理工大学理学院,西安 710048)

1 引 言

第三代宽禁带半导体氮化镓具有高电子饱和速率和击穿电压、强抗腐蚀性以及稳定性好等优势[1,2],且满足高功率、高温度、高线性、高电压、高频率和高效率半导体器件的工作要求[3].为了进一步提高GaN的耐压能力及高频特性,近年来在实验和理论上对GaN及其掺杂体系光电特性的研究越来越多[4−7].GaN晶体中Fe的掺入会使其形成深的受主中心[8],部分因本征缺陷所产生的电子会被激发的空穴所补偿,进而得到呈现高阻特性的材料[9].Fe掺杂GaN材料还表现出极短的有效载流子寿命,因此,一旦去除光触发,基于GaN:Fe的高压光电导开关可以快速地恢复.实验上Polyakov等[10],Feng等[11],Frietas等[12]以及Dashdorj等[13]均从不同方向研究了Fe掺杂GaN材料的光学和电学性质;理论上董艳锋和李英[14]、陆稳和雷天民[15]、黄保瑞等[16]、李倩倩等[17]以及邢海英等[18]均计算了GaN晶体的光学带隙宽度,由于选择方法不同,所得结果均不理想,且与实验值相差较大.本文基于密度泛函理论,利用非局部Perdew-Burke-Ernzerhof(PBE)交换关联泛函和半局部Heyd-Scuseria-Ernzerhof(HSE)杂化交换关联泛函来求解Kohn-Sham方程,计算所得结果与其他方法相比更为准确[19,20];研究了本征GaN以及GaN:Fe体系的光电特性,计算结果与相关实验所得结论一致.

2 理论模型和计算方法

2.1 理论模型

理想GaN晶体的三种结构分别为闪锌矿、纤锌矿和岩盐矿[21],本文所采用的纤锌矿GaN的晶格常数为a=b=3.189 Å,c=5.185 Å[22],α=β=90◦,γ=120◦,c/a=1.626, 属于空间群,为六方密堆积结构.z轴方向Ga—N键长为1.969 Å,其他方向的Ga—N键长为1.965 Å.受计算机计算能力的限制,选取相对较小的每个超晶胞N原子和Ga原子各8个的2×2×1的超级晶胞.掺杂时,Fe原子直接取代1位置处的Ga原子(如图1),掺杂浓度为12.5%.

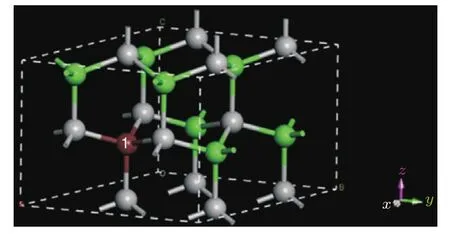
图1 Fe掺杂GaN体系的超胞结构,其中绿色为Ga原子,灰白色为N原子,棕色为掺杂的Fe原子Fig.1.Supercell structure of GaN system doped Fe,the green dots present Ga atoms,the gray dots present N atoms,the brown dot presents Fe element.

2.2 计算方法

本文涉及的所有计算都是使用当前流行且较成功的材料能带结构计算软件包VASP来完成,该软件基于Linux操作系统.在密度泛函理论(DFT)的框架下完成方程的求解过程[23,24],计算中使用比超软赝势(USPP)更加精确的投影缀加波赝势(PAW).利用非局部PBE[25]交换关联泛函和半局部HSE杂化交换关联泛函[26,27]来求解Kohn-Sham方程[28].在杂化泛函中,计算所采用的Hartree-Fock电势的混合参数设置为0.28.平面赝势波截断能选取400 eV,布里渊区K点为6×6×6,能量收敛标准10−5eV.Fe,Ga,N原子的价电子为3p63d64s2,2s22p3,3d104s24p1.

3 计算结果与讨论

3.1 理想GaN和GaN:Fe体系的电子结构

3.1.1 晶体参数

对理想GaN晶体以及掺杂体系进行结构优化,得到的晶格参数数值列于表1.

表1 对理想GaN和GaN:Fe体系的晶胞参数值Table 1.Cell parameters values of ideal GaN and GaN:Fe systems.

从表1可以看出,相比已有实验值,本文的计算结果误差均很好地控制在1%以内.从优化后的数据可以看出Fe掺杂后晶胞的a,b值基本保持不变,c值略有减小.引起c值改变的主要原因有以下几个方面:1)Fe3+的离子半径较Ga3+的离子半径小;2)Fe—N键(1.94 Å)较Ga—N键(1.95 Å)短,且远离Fe的Ga—N键键长都比理想GaN晶体中同方向键长略有减小;3)图1中2—1—3原子之间键角(109.058◦)较6—5—4原子之间键角(109.092◦)减小,3—1—4原子之间键角(109.881◦)较4—5—7原子之间键角(109.848◦)增大.

3.1.2 能带结构

对理想GaN和GaN:Fe体系优化后的结构进行能带计算,得到能带结构参数列于表2,计算所得本征GaN晶体带隙宽度与实验值3.39 eV[29]的误差仅为0.59%.

表2 理想GaN和GaN:Fe体系的带隙参数Table 2.Gap parameters values of ideal GaN and GaN:Fe systems.

理想的GaN体系的能带结构如图2所示,其中价带顶和导带底均位于布里渊区中心点,符合直接带隙半导体的特征,得到3.41 eV的禁带宽度与实验值3.39 eV误差仅0.59%.Fe掺入GaN使得材料电子结构和带隙性质发生了较大改变,可以直观地从能带结构图和电子态密度图中进行了解.图3(a)和图3(b)分别为GaN:Fe体系的自旋向上和向下的能带结构,对于自旋向下的能带结构,可以清楚地看到在导带底多出了几条杂质能级,但仍显示半导体特性,而自旋向上的能带结构中并没有多出杂质能级,只是Fe的掺杂引起导带底位置和价带顶位置距离缩小,从而导致禁带宽度减小为3.06 eV.与理想GaN晶体的能带结构相比,虽然GaN:Fe体系电子结构和带隙性质发生较大改变,但价带顶和导带底均未偏离布里渊区中心点,所以仍然是直接带隙半导体.

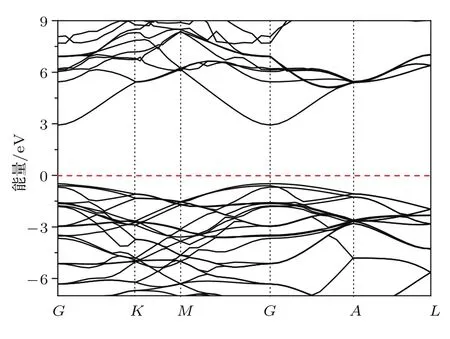
图2 理想GaN体系的能带结构Fig.2.Band structures of ideal GaN systems.

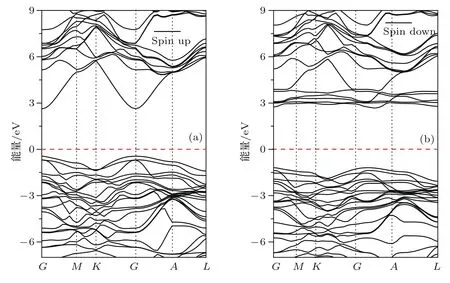
图3 理想GaN:Fe体系的能带结构Fig.3.Band structures of ideal GaN:Fe systems.

3.1.3 电子态密度

图4(a)和图4(b)给出了理想GaN和GaN:Fe体系的总态密度(DOS).

由图4(a)可知,理想GaN晶体的电子所处能级为3组,即带1(约−18.53—−14.69 eV)、带2(约−8.22—−0.33 eV)和带3(约2.96—10.63 eV).N原子的2s态电子主要分布在带1处,其峰值很尖锐,与其他带之间也没有明显的相互作用,表现出较强的局域性;带2左侧峰值主要来源于N的2p态和Ga的4s态,右侧峰值则主要来源于N的2p态和Ga的4p态;带3的峰值主要来源于N的2s,2p态,Ga的3s,4p,4d态.

由图4(b)可见,GaN:Fe体系较本征GaN材料的总态密度分布跨度明显增大,且自旋向上部分(即图4(b)中y轴0刻度上方曲线)与自旋向下部分(即图4(b)中y轴0刻度下方曲线)在导带底及价带顶位置出现了明显的极化现象.对于自旋向上部分的电子态密度图中,带1峰值的来源几乎没有改变,带2部分左侧峰值来源多了Fe的3d态,带3中峰值数明显变多是引起态密度分布跨度增大的主要原因,但其来源并没有明显的变化,是材料中Fe的引入导致电子能量改变.而自旋向下部分的电子态密度图中,导带底位置(即带3起始部分)峰值则主要由Fe的3d态的电子提供.

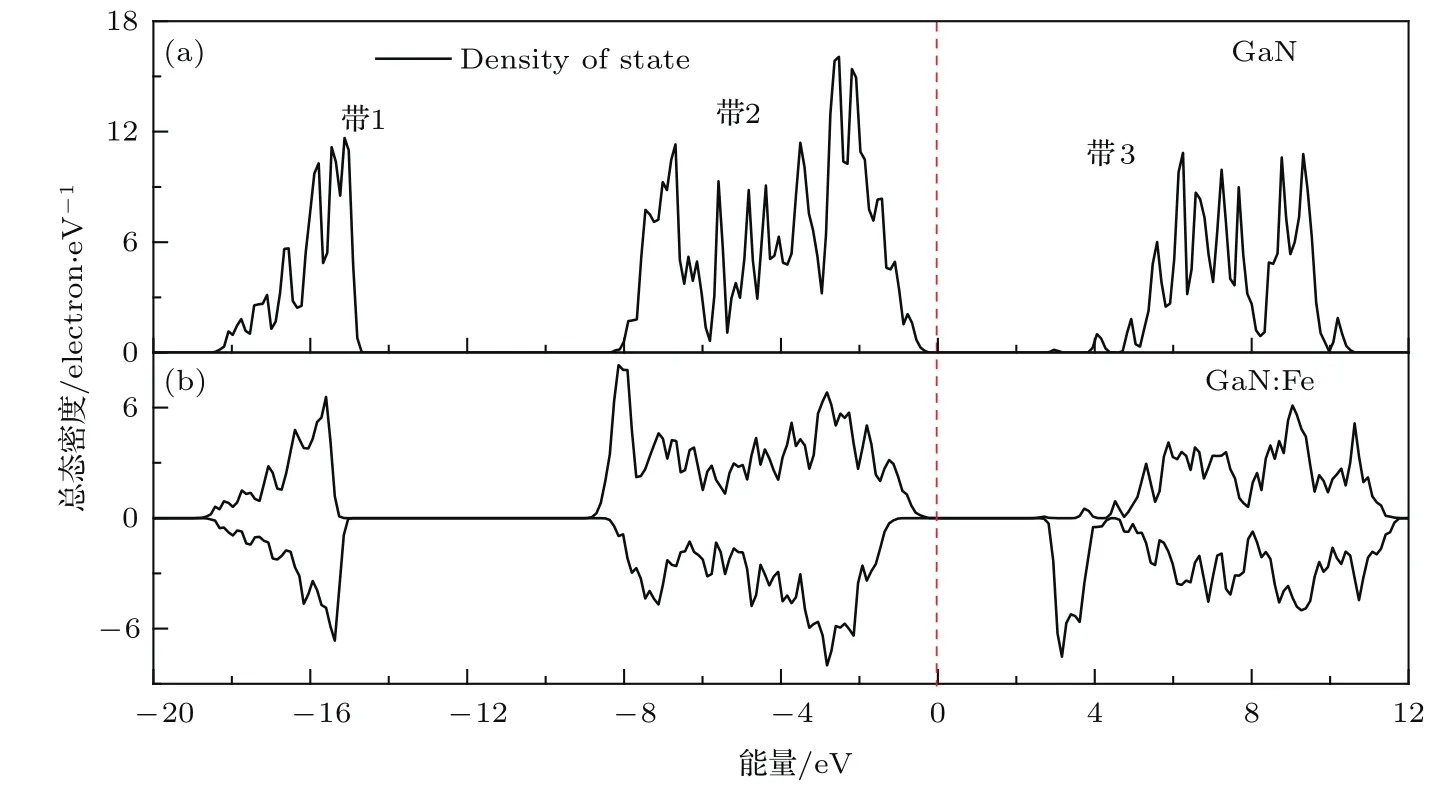
图4 理想GaN和GaN:Fe体系的DOS图Fig.4.DOS diagram of ideal GaN and GaN:Fe systems.

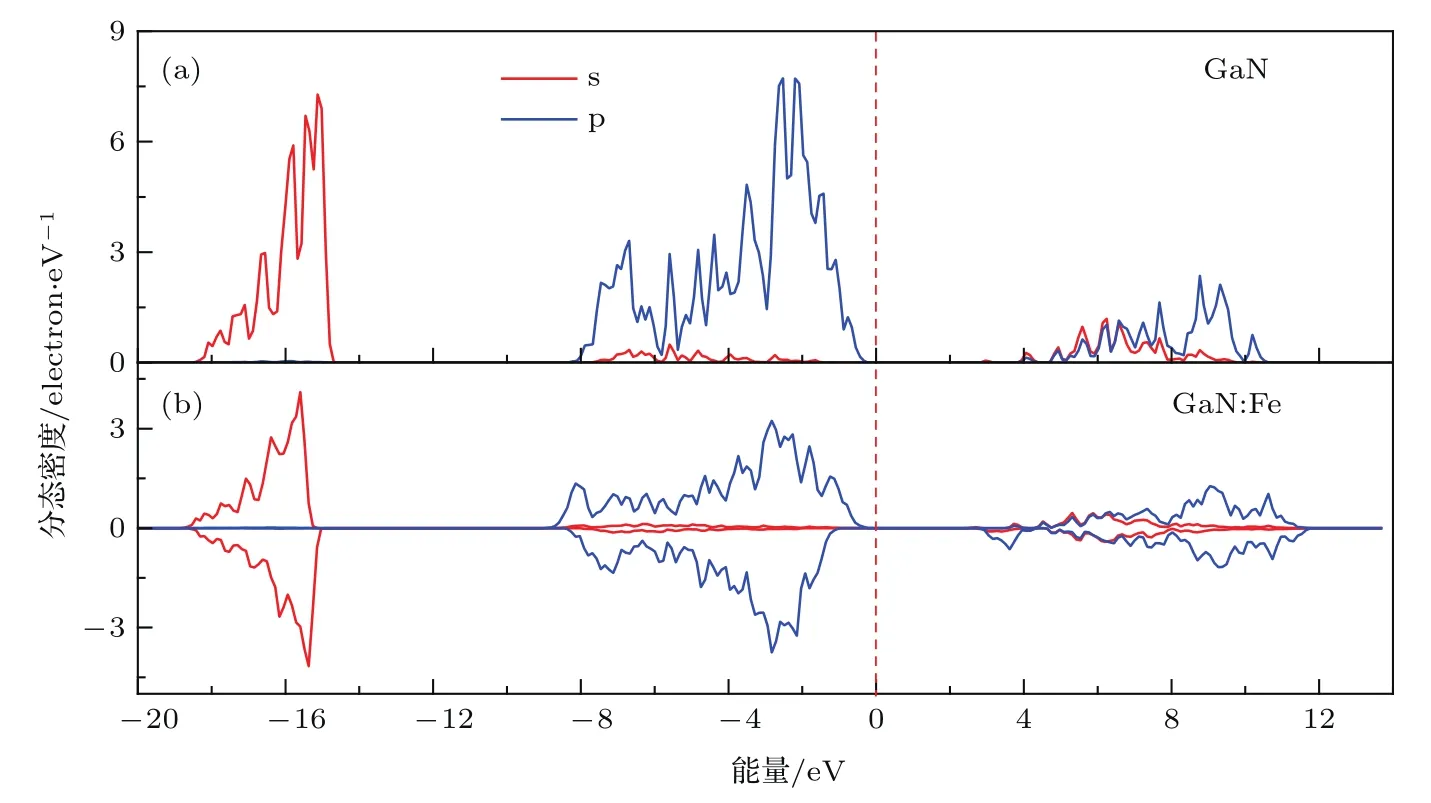
图5 理想GaN和GaN:Fe体系N原子的PDOS图Fig.5.PDOS diagram of N atoms in ideal GaN and GaN:Fe systems.

图5、图6和图7分别为N原子、Ga原子和 Fe原子的分态密度图.从图5和图6可以看出,掺杂使得Ga原子和N原子各状态电子对带3的影响明显改变,3d态的Fe原子自旋向上和向下部分分别对不同带的峰值做出了贡献.

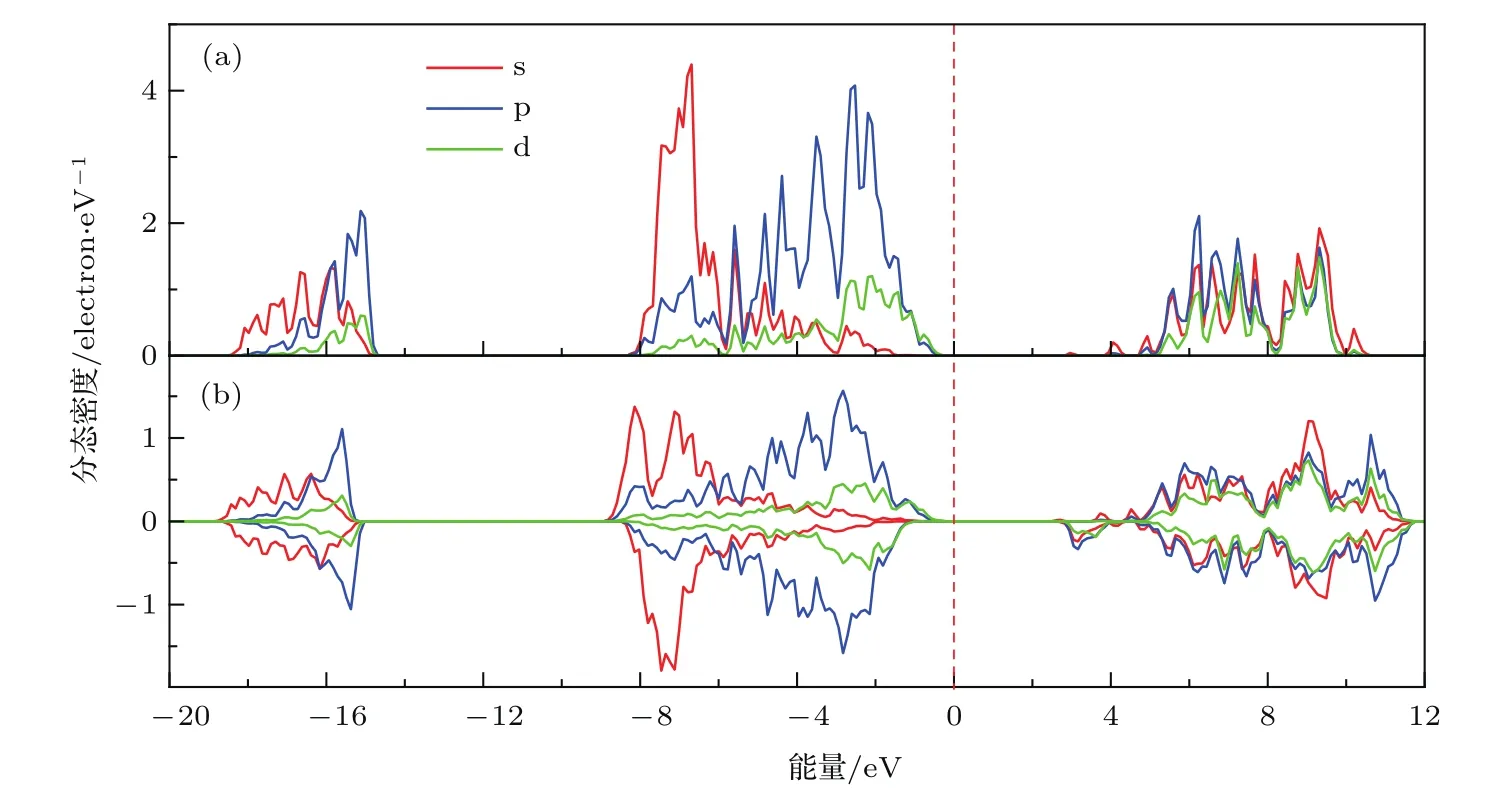
图6 理想GaN和GaN:Fe体系Ga原子的PDOS图Fig.6.PDOS diagram of Ga atoms in ideal GaN and GaN:Fe systems.

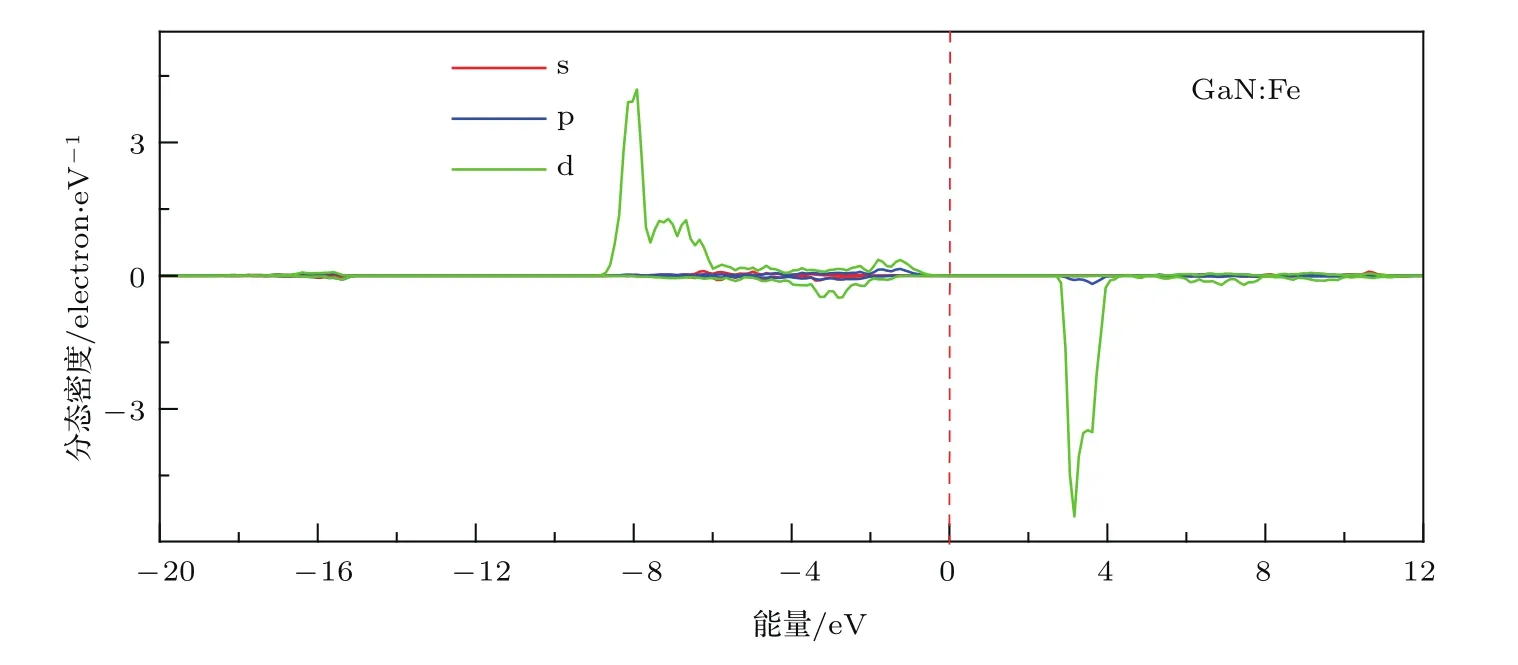
图7 理想GaN和GaN:Fe体系Fe原子的PDOS图Fig.7.PDOS diagram of Fe atoms in ideal GaN and GaN:Fe systems.

3.2 理想GaN和GaN:Fe体系的光学性质

在结构体系中,处理光和固体最有效的办法是单电子近似和绝热近似,处理过程中直接忽略声子的间接跃迁,这是由于声子的频率远小于电子跃迁的频率,所以最终只对电子激发过程进行分析.在波矢较小的情况下,可以用复介电函数ε(ω)=ε1(ω)+iε2(ω)或者复折射率函数N(ω)=n(ω)+iκ(ω)来描述光波在固体中的线性响应情况.其中

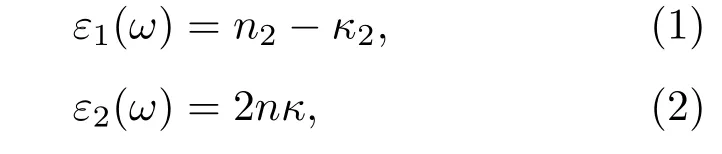
式中n为折射率,κ为消光系数.

通过直接跃迁概率定义和Kramers-Kronig色散关系可以得出晶体的介电函数的实部和虚部为[30]:

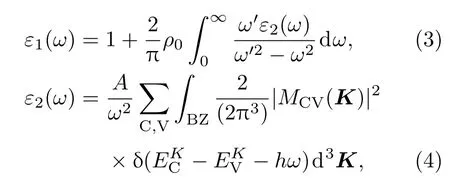
其中下标C,V表示导带和价带,BZ表示第一布里渊区,K为倒格矢,|MCV(K)|2为动量矩阵元,A为与允许直接跃迁吸收系数有关的常数,ω是圆周频率,表示导带和价带的本征能级.

根据晶体的介电函数,诸如吸收谱α(ω)、反射谱R(ω)和能量损失谱L(ω)的光学性质可由下列公式给出[30,31]:

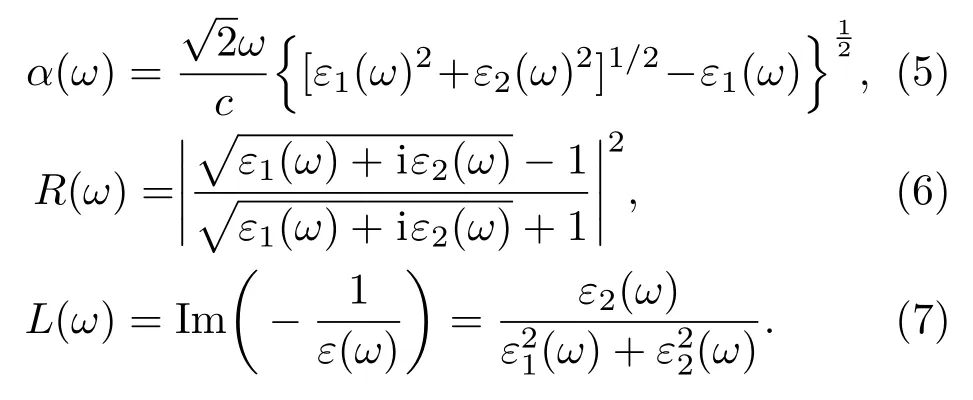
3.2.1 理想GaN和GaN:Fe体系的复介电函数

沟通带间跃迁和固体电子结构的介电函数反映了固体能带结构及各种光谱信息[32].本征GaN和GaN:Fe体系均为直接带隙半导体,其光谱是由能级间电子的直接跃迁所产生,峰值由能带结构和态密度来解释.

图8为理想GaN和GaN:Fe体系的介电函数实部与虚部随入射光子能量变化的曲线.从图8(a)可以看出,本征GaN静态介电常数为5.74,与实验数据5.7[33]一致,且介电函数实部随光子能量变化趋势为先升后降至零以下,之后再上升,结果可靠;掺杂体系中的静态介电常数为6.20,且变化趋势与未掺杂情况基本一致,这说明掺杂使得材料耐高压特性增强.

介电函数虚部决定着材料的光吸收特性,图8(b)为介电函数虚部的变化曲线.可以看出,未掺杂情况两个主峰值对应的光子能量分别为6.81 eV和10.85 eV,根据态密度分析,在6.81 eV处为直接跃迁,并与价带顶到导带底的跃迁有关.掺杂体系在低能区方向约4.04 eV处多出一个峰值,该峰值由价带内部的电子跃迁造成,而原本两个峰值均比之前值要大,这与掺入杂质之后导致吸收峰值增大有关.

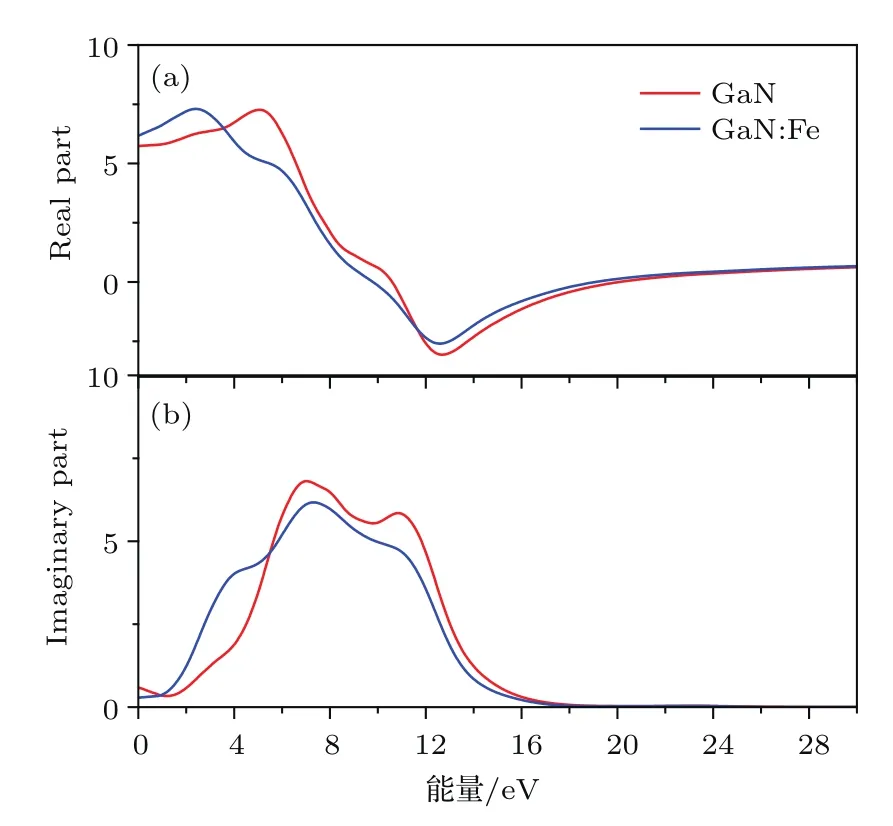
图8 理想GaN和GaN:Fe体系的介电函数实部与虚部Fig.8.Real part and imaginary part of dielectric function in ideal GaN and GaN:Fe systems.

3.2.2 理想GaN和GaN:Fe体系的吸收系数和折射率

图9(a)为理想GaN和GaN:Fe体系的吸收系数,本征GaN的光吸收边为3.25 eV,此能量对应价带顶到导带底的跃迁,小于禁带宽度3.41 eV,这是因为禁带宽度大小等于光学带隙宽度与激子能量之和[34].当光子能量达到13.80 eV左右时,光吸收系数最大,略高于他人计算结果11.71 eV[17],12.5 eV[15].

折射率是光在真空中的传播速度与光在该介质中的传播速度大小的比值,可以用来表示光能量的衰减.从图9(b)中的折射率变化可以看出,当光子的能量为零时,本征GaN和Fe掺杂体系的静态折射率分别为2.39和2.48,其中GaN晶体的折射率与理论值2.2[33]符合得较好,与实验值2.5[35]也较为一致.且两种情况下光子能量分别为18.43 eV和17.71 eV时,折射率最低,此时入射光发生折射的能力也最弱.

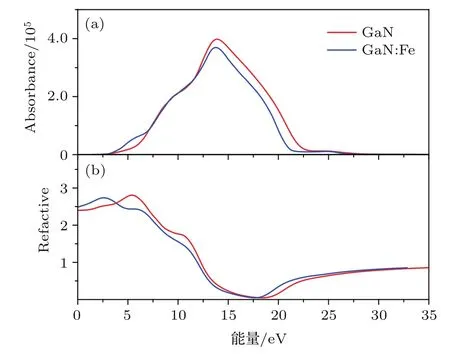
图9 理想GaN和GaN:Fe体系的吸收系数和折射率Fig.9.Absorbance index and refractive index of ideal GaN and GaN:Fe systems.

3.2.3 理想GaN和GaN:Fe体系的能量损失谱、反射率及消光系数

掺杂后体系能量损失最大值降低,且能量损失峰值相对左移.能量损失谱表示电子在材料中快速穿越时能量的损失,其变化曲线如图10(a)所示.未掺杂体系的能量损失最大值在20.02 eV,与实验测得22.5 eV[16]符合得较好.掺杂之后左移至18.96 eV处,最大能量损失值的降低与该处光子能量的大小有关.

反射率变化曲线如图10(b)所示,可以看出静态反射率掺杂前后分别为0.17和0.19,最大反射率所对应的光子能量分别为16.91 eV和17.45 eV.综合吸收系数和折射率变化曲线表明此计算结果可靠.

由图10(c)体系消光系数变化曲线可以看出,未掺杂与掺杂体系均在11.99 eV左右开始出现衰减,掺杂使得体系的衰减峰值有所降低,且光子能量为零时,消光系数值低于本征GaN体系.

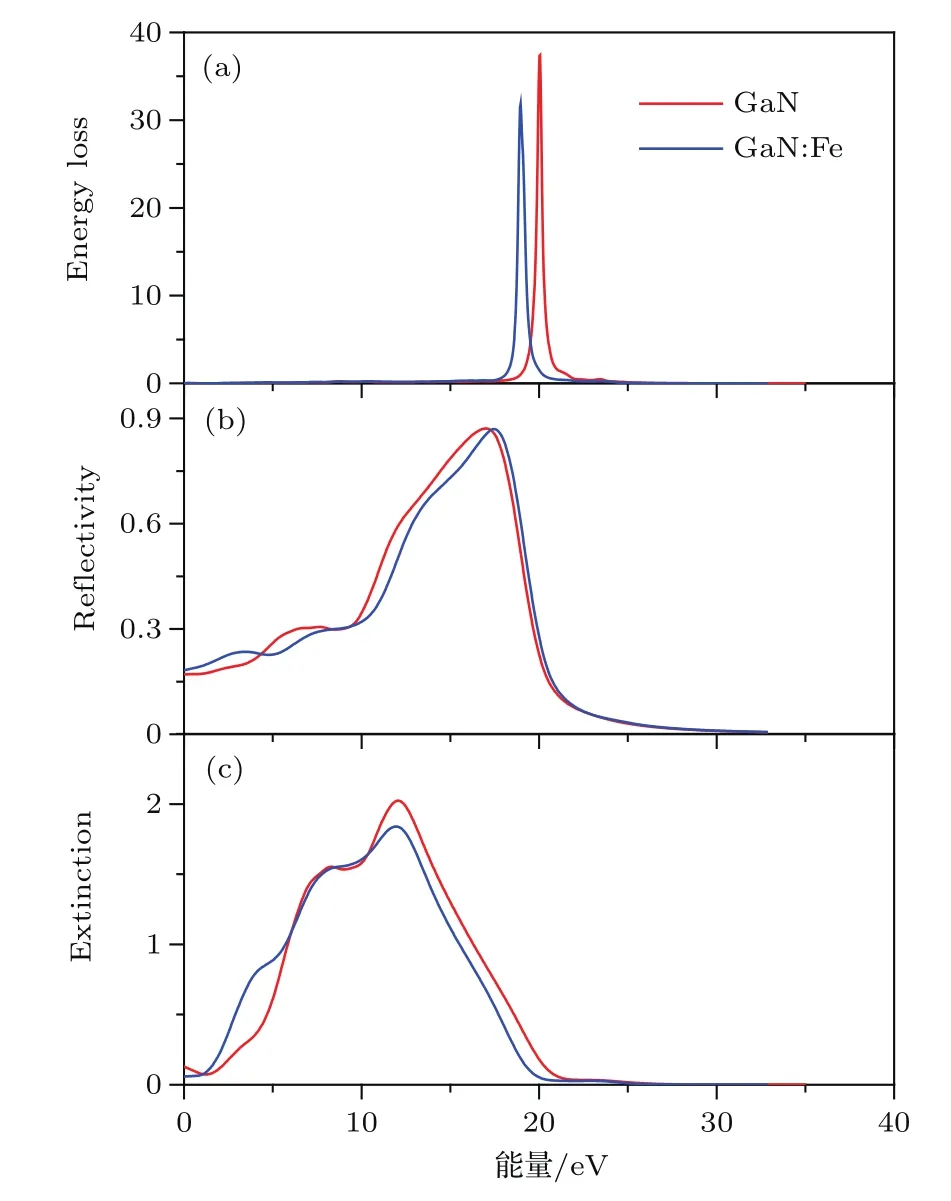
图10 理想GaN和GaN:Fe体系的能量损失谱、反射率和消光系数Fig.10.Energy loss spectroscopy,reflectivity and extinction coefficients of ideal GaN and GaN:Fe systems.

4 结 论

对理想GaN和GaN:Fe体系的超级晶胞结构进行优化,计算了它们的能带结构和电子态分布、介电函数、吸收系数、折射率、反射率、能量损失谱和消光系数.计算结果表明GaN:Fe体系带隙较本征GaN明显变窄,且在禁带中引入局域的杂质能级,该能级主要来源于Fe的3d态电子.理想GaN晶体费米能级位于禁带中间且靠近导带,12.5%的Fe掺杂导致其费米能级更靠近导带,杂质Fe的掺入均不同程度地影响体系的光学特性.计算结果与实验数据一致,为Fe掺杂GaN高压光电导开关材料和器件的进一步研究提供了很好的理论依据.

[1]Fu X Q,Chang B K,Li S 2011Acta Phys.Sin.60 038503(in Chinese)[付小倩,常本康,李飙2011物理学报60 038503]

[2]Brown G F,Wu J Q 2009Laser Photon.Rev.36 394

[3]Zhao Y J 2006Adv.Mater.Industry8 55(in Chinese)[赵亚娟2006先进材料工业8 55]

[4]Lee R,Wright A F,Crawford M H,Petersen G A,Han J,Biefeld R M 1999Appl.Phys.Lett.74 3344

[5]Dridi Z,Bouhafs B,Ruterana P 2003Semicond.Sci.Tech.18 850

[6]Yun F,Reshchikov M A,He L,King T,Morkoc H 2002J.Appl.Phys.92 4142

[7]Kuo Y K,Lin W W 2002Jpn.J.Appl.Phys.41 73

[8]Baur J,Maier K,Kunzer M,Kaufmann U,Schneider J,Amano H,Hiramatsu K 1994Appl.Phys.Lett.64 857

[9]Cordier Y,Azize M,Baron N,Bougrioua Z,Chenot S,Tottereau O,Gibart P 2008J.Cryst.Growth310 948

[10]Polyakov A Y,Smirnov N B,Govorkov A V,Pearton S J 2003Appl.Phys.Lett.83 3314

[11]Feng Z H,Liu B,Yuan F P,Yin J Y,Liang D,Li X B,Cai S J 2007J.Cryst.Growth309 8

[12]Freitas J A,Gowda M,Tischler J G,Kim J H,Liu L,Hanser D 2008J.Cryst.Growth310 3968

[13]Dashdorj J,Zvanut M E,Harrison J G,Udwary K,Paskova T 2012J.Appl.Phys.112 013712

[14]Dong Y F,Li Y 2016Chin.J.Comput.Phys.33 490(in Chinese)[董艳锋,李英2016计算物理33 490]

[15]Lu W,Lei T M 2009Electron.Sci.Tech.22 55(in Chinese)[陆稳,雷天民 2009电子科技 22 55]

[16]Huang B R,Zhang F C,Cui H W 2016Henan Sci.34 16(in Chinese)[黄保瑞,张富春,崔红卫 2016河南科学34 16]

[17]Li Q Q,Hao Q Y,Li Y,Liu G D 2013Acta Phys.Sin.62 017103(in Chinese)[李倩倩,郝秋艳,李英,刘国栋2013物理学报62 017103]

[18]Xing H Y,Fan G H,Zhao D G,He M,Zhang Y,Zhou T M 2008Acta Phys.Sin.57 6513(in Chinese)[邢海英,范广涵,赵德刚,何苗,章勇,周天明2008物理学报57 6513]

[19]Zhao Y Q,Liu B,Yu Z L,Ma J,Wan Q,He P B,Cai M Q 2017J.Mater.Chem.C5 5356

[20]Zhao Y Q,Liu B,Yu Z L,Cao D,Cai M Q 2017Electrochim.Acta247 891

[21]Gorczyca I,Christensen N E,Perlin P 1991Solid State Commun.79 779

[22]Leszcynski M,Grzegory I,Bockowski M 1993J.Cryst.Growth126 601

[23]Liu B,Wu L J,Zhao Y Q,Wang L Z,Cai M Q 2016Eur.Phys.J.B89 80

[24]Cao D,Liu B,Yu H,Hu W,Cai M 2015Eur.Phys.J.B88 75

[25]Perdew J P,Burke K,Ernzerhof M 1996Phys.Rev.Lett.77 3865

[26]Wu L J,Zhao Y Q,Chen C W,Wang L Z,Liu B,Cai M Q 2016Chin.Phys.B25 107202

[27]Liu B,Wu L J,Zhao Y Q,Wang L Z,Cai M Q 2016J.Magn.Magn.Mater.420 218

[28]Hummer K,Harl J,Kresse G 2009Phys.Rev.B80 115205

[29]Maruska H A,Tietjen J J 1969Appl.Phys.Lett.15 327

[30]Brown G F,Wu J Q 2009Laser Photon.Rev.3 394

[31]Wang L Z,Zhao Y Q,Liu B,Wu L J,Cai M Q 2016Phys.Chem.Chem.Phys.18 22188

[32]Sheng X C 2003The Spectrum and Optical Property of Semiconductor(Beijing:Science Press)p76(in Chinese)[沈学础 2003半导体光谱和光学性质 (科学出版社)第76页]

[33]Pankove J I,Berkeyheiser J E,Maruska H P 1970Solid State Commun.8 1051

[34]Choi J H,Cui P,Lan H,Zhang Z 2015Appl.Phys.Lett.115 066403

[35]Maruska H P,Tietjen J J 1969Appl.Phys.Lett.15 327