极化控制的双波段宽带红外吸收器研究∗

杨鹏 韩天成

(西南大学物理科学与技术学院,重庆 400715)

1 引 言

基于电磁超构材料的完美吸收器(perfect metamaterial absorber,PMA)通过合理设计单元结构可实现对特定频段电磁波的100%吸收,与传统的吸波材料相比,它具有吸波强、厚度薄、质量轻、吸波频段灵活可调等诸多优点[1],在等离子体传感器[2]、热电子光探测器[3]、红外隐身[4]、辐射制冷[5,6]等方面有重要应用前景.Landy等[7]首次提出的PMA是由表层金属谐振环(electric ring resonators,ERRs)、中间的介质层以及底部的金属线组成,该结构仅在单频实现了完美吸收,且只对横磁(transverse magnetic,TM)波有效.随后,底层是金属板的金属-介质-金属(metal-insulatormetal,MIM)型PMA由于其高吸收率已被广泛研究[8−10].然而,窄带吸收限制了PMA的应用,利用高损耗材料[11,12]或金字塔型多层结构[13,14]可以有效地拓宽吸收频带.

一维光栅型吸收器由于其结构简单、易于加工的优势备受关注,然而其不足之处是频带很窄且只对一种极化有效[15,16],这是由于导致吸收的磁激元共振的激发需要一个与结构截面垂直的磁场分量.为了拓宽吸收频带,人们提出了在一个周期单元内放置两个不同尺寸的金属条[17]、四个不同尺寸的金属条[18]以及金字塔型多层结构[19],然而这些结构都只能吸收TM波,对横电(transverse electric,TE)波无效.随后,Wu等[20]基于导波模式谐振实现了一维光栅型结构对TE波的吸收.Chern等[21]提出了利用介质-金属光栅-介质的三层结构分别实现TM波和TE波的吸收.Feng等[22]提出了利用两层金属-介质双层膜垂直层叠的方法,同时实现了对TM波和TE波的吸收,但是吸收频带非常窄(几乎是单频),这就使得其应用价值大打折扣.

本文基于光栅结构实现了对TM波和TE波的高效、宽频吸收,对TM波在1.68—2µm波段吸收超过90%,对TE波在3.8—3.9µm波段吸收超过90%.与Feng等[22]的结果相比,本文提出的结构极大地拓宽了吸收带宽,且不同的极化波对应不同的吸波频段,为其应用提供了更多的选择和更大的灵活性.

2 结构设计

本文提出的双波段宽带红外吸收器的基本结构单元如图1(a)所示.该吸收器由金属底板和八个尺寸渐变的子单元组成,每一个子单元由两层金属-介质双层膜垂直层叠组成.通过仿真优化确定的基本结构单元周期P为11µm,金属底板上每个子单元周期S为1.45µm,上层介质厚度d和下层介质厚度t分别为0.69µm 和0.2µm,金属层的厚度h均为0.05µm.沿着x方向,八个子单元的宽度w依次为w1=0.23µm,w2=0.223µm,w3=0.215µm,w4=0.205µm,w5=0.203µm,w6=0.2µm,w7=0.18µm,w8=0.179µm,在y方向上为无限长.

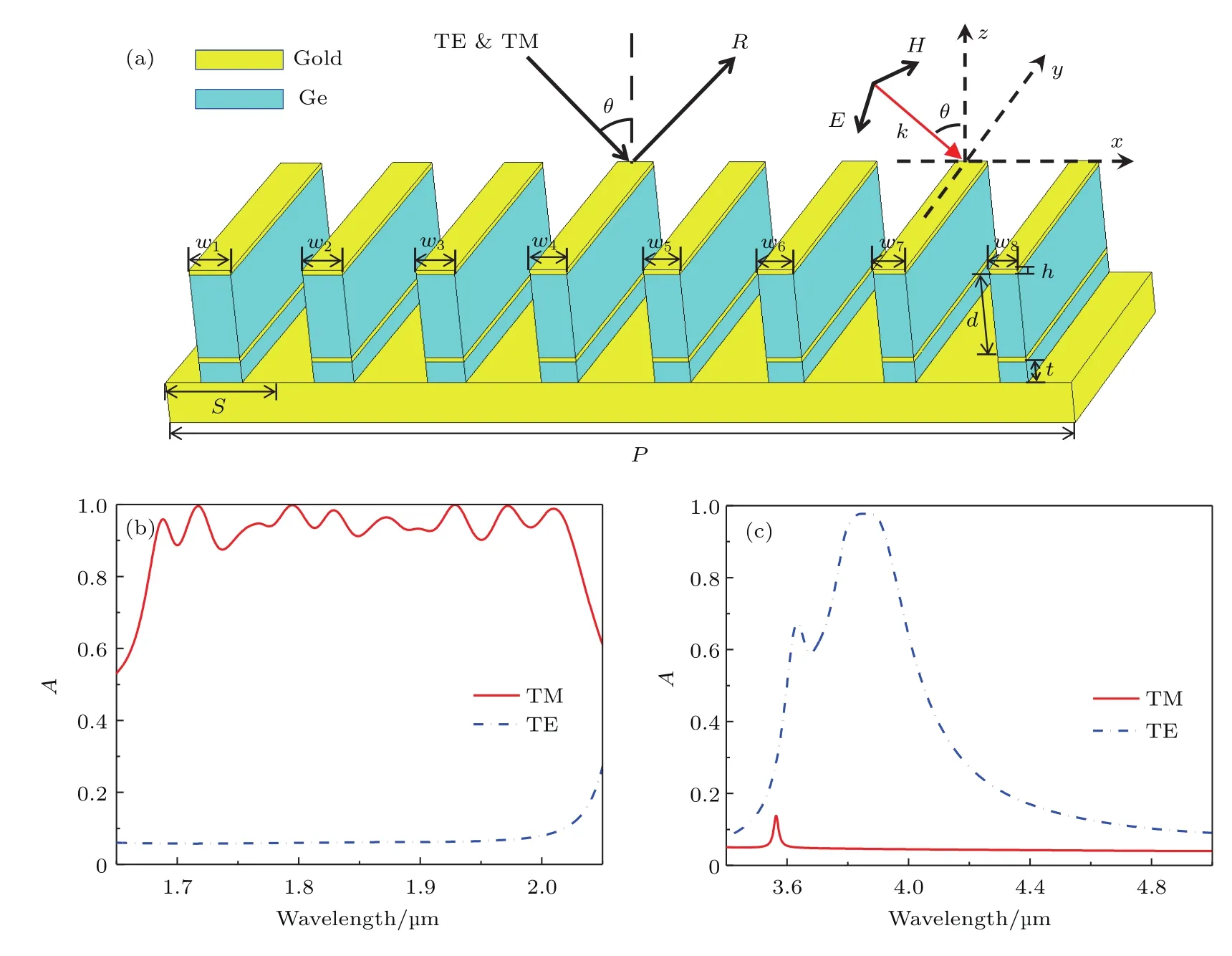
图1 (a)吸收器的基本结构单元示意图;(b)对TM波吸收超过90%的吸收谱;(c)对TE波吸收超过90%的吸收谱Fig.1.(a)Schematic diagram of the basic unit of the proposed absorber;(b)absorption spectrum for TM wave above 90%;(c)absorption spectrum for TE wave above 90%.

3 数值模拟与分析

基于有限元方法对所设计的双波段宽带红外吸收器进行了数值模拟.仿真中将x,y方向的边界条均设置为周期边界条件,采用平面电磁波作为入射激励源.结构设计中的所有金属材料均为金,其电导率为4.56×107S/m.介质层材料选为锗(Ge),这是一种折射率n=4的无损材料[23].通过结构尺寸的优化,可以调控该吸收器的等效介电常数和等效磁导率,使二者接近一致.此时,红外吸收器与空气界面将满足阻抗匹配条件,从而实现对特定频率的电磁波的吸收.吸收率A可表示为A(ω)=1−T(ω)−R(ω),其中ω表示入射电磁波的角频率,T(ω)表示能量透射率,R(ω)表示能量反射率.由于底部为金属板,因此透射率T(ω)=0,则可以得到A(ω)=1−R(ω).

在垂直入射的情况下,不同波段的吸收谱如图1(b)和图1(c)所示,红色和蓝色分别代表TM波和TE波的吸收谱,其中,入射波的电场方向垂直于xz平面时为TE波,入射波的电场方向平行于xz平面时为TM波.图1(b)显示对TM波在1.68—2µm波段的吸收率超过90%,而对TE波的吸收非常小(<6%).图1(c)显示对TE波在3.8—3.9µm波段的吸收率超过90%,而对TM 波的吸收非常小(<5%).因此,本文所提出的结构实现了对TM波和TE波在不同波段的独立吸收.

为了深入理解本文提出的红外吸收器的电磁吸收机理,我们以单个子单元为考察对象,其结构如图2(a)所示.当入射波为TM波时,随着wi的变化子单元的吸收谱如图2(b)所示.在这里,子单元结构参数为S′=1.05µm,w1=0.24µm,w2=0.23 µm,w3=0.223 µm,w4=0.215 µm,金属层和介质层的厚度与图1(a)中的一致.从图2(b)可以看出,子单元有两个较好的吸收峰,且吸收峰随着子单元尺寸的变化而发生平移.通过激发多谐振耦合[24],使得吸收频点有效地连接起来(整体的吸收效率大于90%),从而可以达到宽带吸收的效果.这正是本文提出的吸收器在TM波下呈现出宽带吸收的物理机理.接下来考察子单元在谐振吸收峰处的电场分布,以w3为例,共振波长在1.74µm和1.86µm处的电场分布如图2(c)和图2(d)所示.从图中可以看出,当共振波长为1.74µm时,电场主要集中在较低层金属带的两侧.这是由于电场环绕在分离层周围形成涡旋电流[25],从而感应出一个较强的磁场,感应磁场与入射磁场会产生强相互作用,从而产生磁激元共振,这是实现电磁吸收的主要原因.同理,共振波长在1.86µm处时,可以看到电场同时集中在上下两层金属带的两侧,此时的磁激元共振更强一些,导致吸收率接近100%.

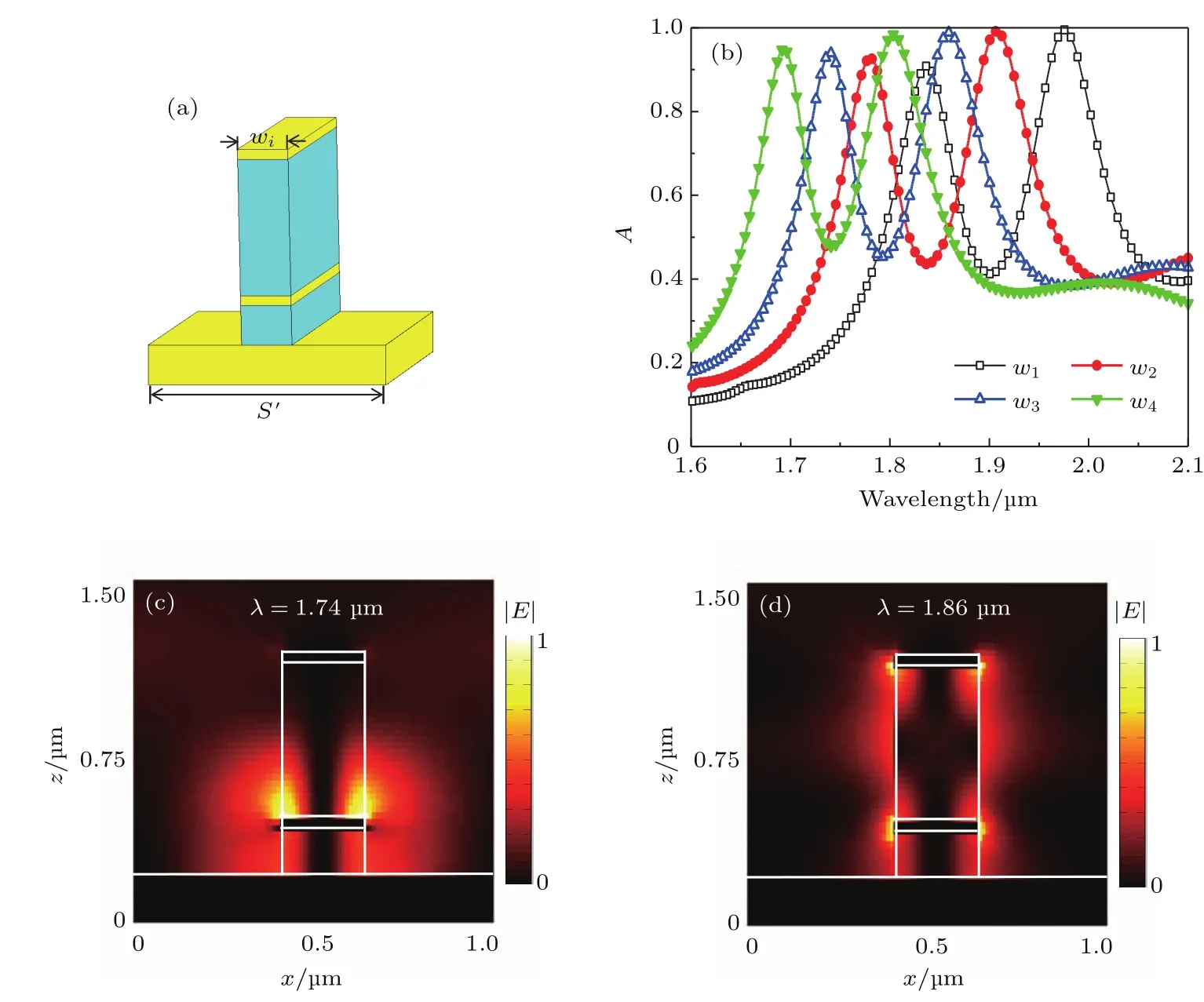
图2 (a)子单元的结构示意图;(b)不同尺寸的子单元对TM波的吸收谱;(c)入射波长为1.74µm时的电场分布;(d)入射波长为1.86µm时的电场分布Fig.2.(a)Schematic diagram of a subunit;(b)absorption spectrum under TM wave with the change of wi;(c)the electric field distribution at λ =1.74 µm;(d)the electric field distribution at λ =1.86 µm.

当入射波是TE波时,随着wi的变化,吸收谱如图3(a)所示.可以看出,不同尺寸的子单元对TE波的吸收峰几乎都达到了100%,实现了完美吸收.然而,随着子单元尺寸的变化,吸收峰的平移量比较小,这就是本文所提出的吸波器对TE波的吸收带宽没有TM波宽的原因.进一步,考察子单元w3在共振波长为4µm时的电场分布,如图3(b)所示.可以看到电场主要集中在上介质层,这是由于导波模式谐振的激发从而实现了完美吸收[21,22].为了更直观地理解多谐振的耦合吸收,以TE波为例,考察整个单元在不同波长下的电场分布,如图4所示.从图中可以看出,随着入射波长的减小,谐振单元从大尺寸子单元向小尺寸子单元转移,并且每个波长都对应多个谐振单元.

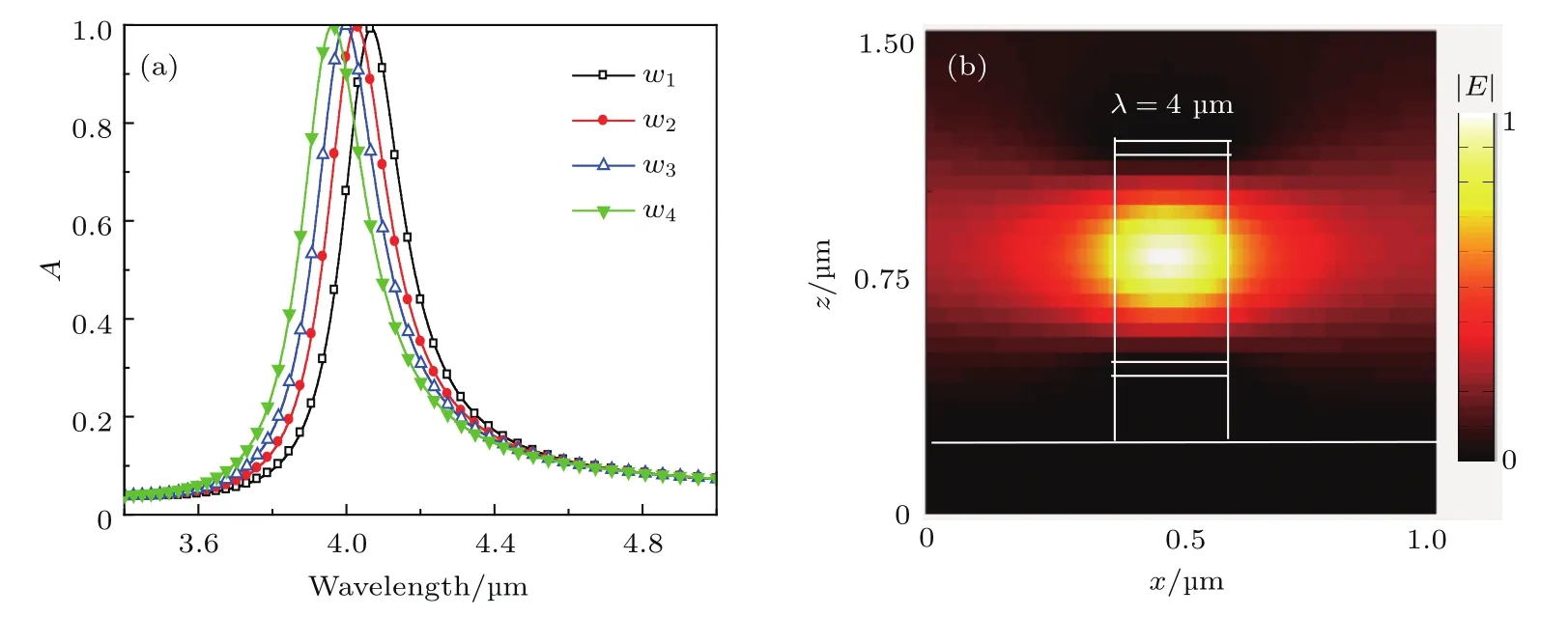
图3 (a)不同尺寸的子单元对TE波的吸收谱;(b)子单元的电场分布Fig.3.(a)Absorption spectrum of the subunit under TE wave with the change of wi;(b)the electric field distribution of the subunit at λ =4 µm.

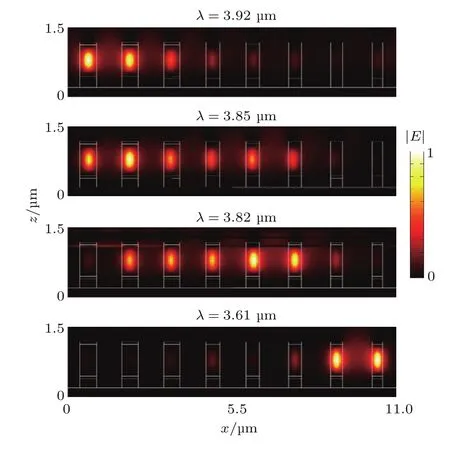
图4 整个单元在TE波入射下的归一化电场分布Fig.4.The normalized electric field distribution for the whole unit under TE wave incidence.

在实际应用中,空间传输的电磁波常常来自于不同的方向,这就要求吸收器具有宽角度吸收特性.为了检验所提出的结构在不同入射角度下的性能表现,TM波和TE波在不同入射角度时的吸收谱分别如图5(a)和图5(b)所示.首先,对TM波,当入射角小于20◦时,能够保持吸波带宽不变且吸收率都在90%以上.但是随着角度的增大,吸收率会有所下降,这主要是由于随着入射角度的增加,结构间的谐振磁通量将变小.总体而言,即便是入射角达到60◦,对TM波依然保持了较宽的吸波频带和较高的吸收效率.对TE波,不同角度入射时的吸收谱如图5(b)所示,随着入射角度的增大,吸收率始终保持较高,但吸收频带的中心波长会向短波方向逐渐偏移,这是由于结构单元的等效电容和电感随着电磁波入射角度的增加逐渐变小,由于谐振频率反比于这两个参量,因而将向高频逐渐偏移[26].

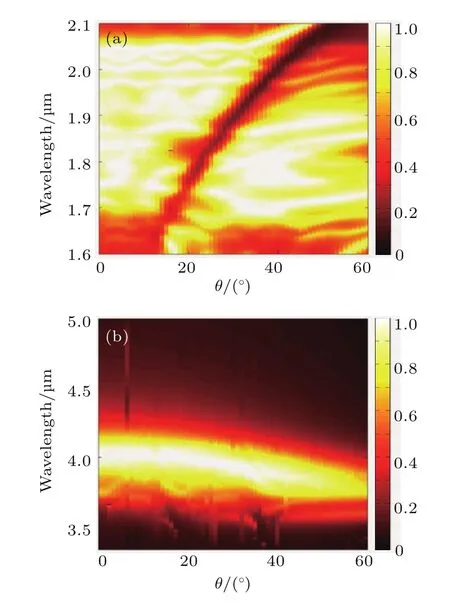
图5 宽入射角度吸收器的吸收谱 (a)TM波入射;(b)TE波入射Fig.5. Absorption spectrum of the proposed absorber under the illumination of a broad incident angle:(a)TM wave incidence;(b)TE wave incidence.

值得注意的是,对TM波的吸收谱中(如图5(a)所示),出现了一条由短波长向长波长逐渐变化的吸收断裂带.为分析其原因,我们考察当入射波长为1.9µm时,电磁波入射角分别为θ=10◦,θ=34◦,θ=50◦时的电场分布,如图6所示.由电场分布可以看出,当θ=10◦和θ=50◦时,电磁谐振会出现在不同的子单元上,从而能够实现较好的吸收.而当θ=34◦时,所有的子单元都未发生电磁谐振,因此几乎没有任何吸收.

进一步,以子单元w1为例,考察TM波在不同入射角度下的吸收谱,如图7所示.可以看到,随着入射角度的增加,子单元w1的下层介质的吸收峰逐渐偏移且向上层介质的吸收峰靠近,从而影响上层介质对电磁波的吸收,当达到特定角度时(15◦),吸收几乎为零.其他子单元也会出现类似的现象.这就能够直观地解释本文提出的吸波结构为何随入射角的变化会出现一条如图5(a)所示的吸收断裂带.

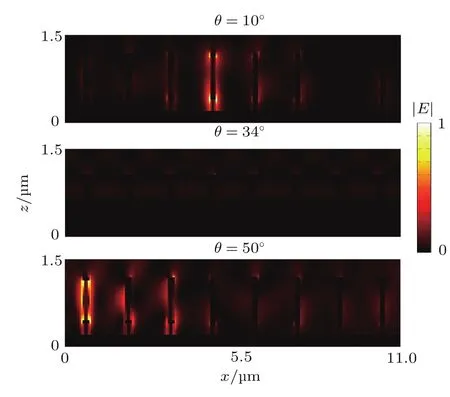
图6 TM波在不同入射角度下的电场分布(λ=1.9µm)Fig.6.Distributions of electric field under TM wave at λ =1.9 µm with different incident angles.

图7 子单元w1对TM波的宽入射角度吸收谱Fig.7.Absorption spectrum for the subunit w1under TM wave with the change of incident angle.

4 结 论

提出了一种基于光栅结构的双波段宽带吸收器,其基本单元由八个梯度排列的子单元构成,每个子单元由两层金属-介质双层膜垂直层叠组成.该结构能够同时吸收TM波(在1.68—2µm吸收率超过90%)和TE波(在3.8—3.9µm吸收率超过90%),且不同的极化波对应不同的吸波频段,这一特性为其应用提供了更大的灵活性.另外,该结构具有宽角度吸收特性,当入射角增大到60◦时仍然能够保持较高的吸收率和较宽的吸收频带.所提设计方法可推广至THz和微波频段.

[1]Watts C M,Liu X,Padilla W J 2012Adv.Mater.24 OP98

[2]Liu N,Mesch M,Weiss T,Hentschel M,Giessen H 2010Nano Lett.10 2342

[3]Li W,Valentine J 2014Nano Lett.14 3510

[4]Shen L,Zhang B,Liu Z,Wang Z,Lin S,Dehdashti S,Li E,Chen H 2015Adv.Opt.Mater.3 1738

[5]Raman A P,Anoma M A,Zhu L,Rephaeli E,Fan S 2014Nature515 540

[6]Zhai Y,Ma Y,David S N,Zhao D,Lou R,Tan G,Yang R,Yin X 2017Science355 1062

[7]Landy N I,Sajuyigbe S,Mock J J,Smith D R,Padilla W J 2008Phys.Rev.Lett.100 207402

[8]Hao J,Wang J,Liu X L,Padilla W J,Zhou L,Qiu M 2010Appl.Phys.Lett.96 4184

[9]Wang J,Chen Y,Hao J,Yan M,Qiu M 2011J.Appl.Phys.109 074510

[10]Liu X,Starr T,Starr A F,Padilla W J 2010Phys.Rev.Lett.104 207403

[11]Ding F,Dai J,Chen Y,Zhu J,Jin Y,Bozhevolnyi S I 2016Sci.Rep.6 39445

[12]Luo M,Shen S,Zhou L,Wu S,Zhou Y,Chen L 2017Opt.Express25 16715

[13]Wu J 2016Opt.Mater.62 47

[14]Li L,Lü Z 2017J.Appl.Phys.122 055104

[15]Zhu P,Guo L J 2012Appl.Phys.Lett.101 051105

[16]Feng R,Ding W,Liu L,Chen L,Qiu J,Chen G 2014Opt.Express22 A335

[17]Koechlin C,Bouchon P,Pardo F,Jaeck J,Lafosse X,Pelouard J L,Haidar R 2011Appl.Phys.Lett.99 241104

[18]Cui Y,Xu J,Fung K H,Jin Y,Kumar A,He S,Fang N X 2011Appl.Phys.Lett.99 193

[19]Cui Y,Fung K H,Xu J,Ma H,Jin Y,He S,Fang N X 2012Nano Lett.12 1443

[20]Wu J,Zhou C,Yu J,Cao H,Li S,Jia W 2014Opt.Commun.329 38

[21]Chern R L,Chen Y T,Lin H Y 2010Opt.Express18 19510

[22]Feng R,Qiu J,Cao Y,Liu L,Ding W,Chen L 2015Opt.Express23 21023

[23]Palik E D 1985Handbook of Optical Constants of Solids(Manhattan:Academic Press)p189

[24]Zhang K L,Hou Z L,Bi S,Fang H M 2017Chin.Phys.B26 127802

[25]Qiu C W,Hao J,Qiu M,Zouhdi S 2012Opt.Lett.37 4955

[26]Sakurai A,Zhao B,Zhang Z M 2014J.Quant.Spectrosc.Radiat.Transfer149 33