非共振圆偏振光作用下单层二硫化钼电子结构及其自旋/谷输运性质∗

张新成 廖文虎 左敏

(吉首大学物理与机电工程学院,吉首 416000)

1 引 言

近10多年来,以石墨烯为代表的二维材料因为其优异的物理性质和器件设计方面的应用前景引起了物理、材料、信息等领域的广泛关注[1,2].边缘功能化[3]、微纳结构化[4]、化学掺杂[5]等方法能够在一定程度上打开石墨烯的带隙,但无带隙的本征能带结构[6,7]使得石墨烯基场效应晶体管截止电流较高、电流开关比较低[8].与石墨烯几何结构类似的单层二硫化钼(MoS2)是直接带隙半导体,具有自旋/谷霍尔效应等物理特性[9−13],从器件设计和应用角度看比石墨烯更加优异,近年来成为新型半导体材料的研究热点之一[14−20].

2011年,Kis等[14]成功地制备了单层MoS2场效应晶体管,后来Liu研究组[15]采用原子层沉积技术成功制作出迁移率高达517 cm2/(V·s)的MoS2场效应晶体管,Zhang等[16]利用离子液体作为栅极制造出具有较高空穴迁移率的单层MoS2场效应晶体管.2012年,Xiao等[17]和Cao等[18]发现单层MoS2在六边形布里渊区顶点附近具有“谷”状能带结构,相邻顶点的谷对左、右旋光具有近乎完美的选择性.香港大学和哥伦比亚大学的实验组通过圆偏振光抽运方法验证了单层MoS2具有偏振光选择性和谷霍尔效应[19,20].2016年,Sengupta和Bellotti[21]研究了非共振圆偏振光作用下二维过渡族金属硫化物自旋霍尔电导,单层MoS2在应力和磁近邻交换场作用下的输运性质也受到关注[22,23],外部电场和近邻交换相互作用被证明是调控单层MoS2能带结构[24−26]的有效手段.然而,很少有相关工作涉及外部非共振圆偏振光对单层MoS2电子能带结构和自旋/谷输运特性的影响,本文针对这方面的问题开展研究.

利用紧束缚近似下的低能有效哈密顿模型和久保线性响应理论,研究了外部非共振圆偏振光对单层MoS2电子能带结构及其自旋/谷输运性质的影响.研究结果表明:单层MoS2布里渊区K谷和K′谷附近自旋依赖的子带间能隙随着非共振右旋圆偏振光引起的有效耦合能分别线性增大和先减小后增大,随着非共振左旋圆偏振光引起的有效耦合能分别先减小后增大和线性增大,实现了有趣的半导体-半金属-半导体转变.在没有非共振圆偏振光作用时,单层MoS2量子化自旋霍尔电导为0、谷霍尔电导为2e2/h;当非共振圆偏振光有效耦合能绝对值在0.79—0.87 eV范围内变化时,系统自旋霍尔电导为−2e2/h、谷霍尔电导为0;当非共振圆偏振光引起的有效耦合能在其他范围内变化时,量子化自旋/谷霍尔电导与无外场时相同.系统自旋极化率在非共振圆偏振光有效耦合能±0.79 eV附近达到最大并发生由正到负或由负到正的急剧转变,谷极化率随着非共振圆偏振光有效耦合能先增大后减小,在非共振圆偏振光有效耦合能绝对值0.79—0.87 eV范围内达到100%.因此,外部非共振圆偏振光是调控单层MoS2量子化霍尔电导、自旋/谷霍尔电导以及自旋/谷极化的有效手段.

2 模型与方法

如图1所示,我们构建了一个基于单层MoS2的场效应晶体管模型,其中单层MoS2置于中心区域并受到非共振圆偏振光的辐照,系统有效哈密顿量为[10,17,27,28]

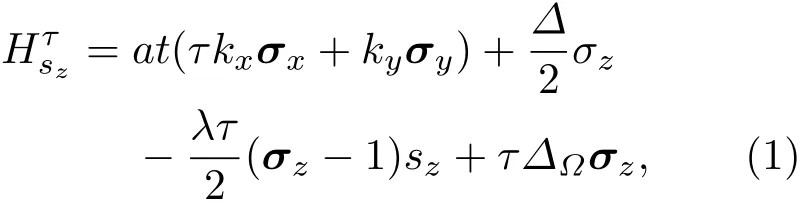
此外,非共振圆偏振光引起的电磁势可以描述为

图1 由金属源极、漏极和可调制背电极构成MoS2纳米场效应管模型图,其中心区域受到非共振圆偏振光的辐照,黑色小球代表钼原子(Mo),黄色小球代表硫原子(S)Fig.1.Schematic representation of the MoS2based fi eld e ff ect transistor,consisting of metallic source,drain and electrically modulated back-gate,with the central region irradiated by the o ff-resonant circularly polarized light(demonstrated by the wave lines),and the black and yellow balls indicates the molybdenum(Mo)and sulfur(S)atoms,respectively.

其中+和−分别表示右旋和左旋圆偏振光,Ω为非共振圆偏振光的频率,A为非共振圆偏振光的振幅.电磁势满足时间周期性条件,即A(t+T)=A(t),周期T=2π/Ω.通过正则变换获得非共振圆偏振光辐照对体系的影响,含时哈密顿量为

当非共振圆偏振光光子能量远大于最近邻跃迁能时,非共振圆偏振光对体系的影响可通过Floquet理论[28,29]简化为有效静态(不含时的)哈密顿量∆Hτ.非共振圆偏振光属于高频弱场,不直接激发体系中的电子,而是通过光子吸收和发射过程改变体系的电子能带结构.先吸收光子后发射光子过程中对体系哈密顿量的改变为,其中分别为电子能量和光子能量,先发射光子后吸收光子过程中对体系哈密顿量的改变为,其中,

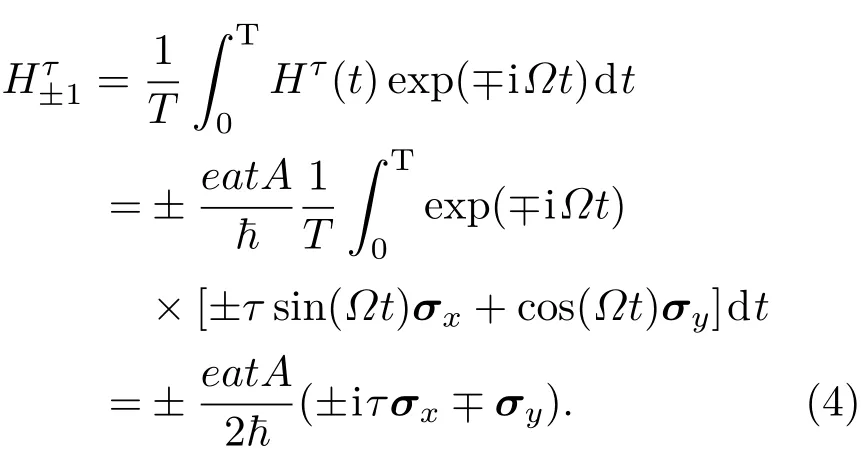
因此,非共振圆偏振光对体系电子能带结构的影响[28,30]为

忽略高阶小量后,获得非共振圆偏振光辐照引起的有效耦合能∆Ω=±a2t2e2A2/h3Ω,其中+和−分别表示右旋和左旋圆偏振光.

通过对角化公式(1)中的哈密顿量,可以得到如下色散关系:

其中,,根号外的+和−分别对应导带(c)和价带(v),对应的导带与价带波函数分别为

我国对农业机械的需求量较大，然而在相关技术研发方面的投入却与需求量不成比例，其中技术研发人员、研发基础技术、研发所需设备缺口量较大，导致我国农业机械技术的研发进度相对迟缓，无法满足我国农业机械化发展的需求。

和

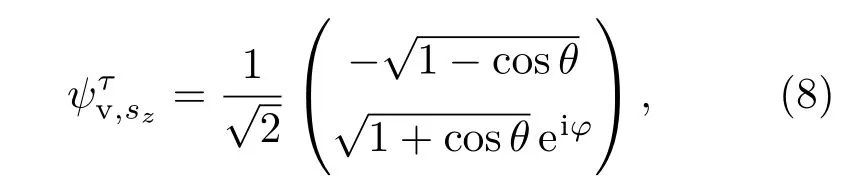
利用久保线性响应理论[31−34],可以得到自旋和谷依赖的横向霍尔电导:

其中S为系统面积,

为费米-狄拉克分布函数,η为无穷小量.可以进一步得到系统的自旋霍尔电导[35,36]

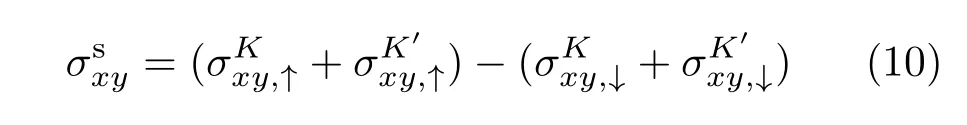
和谷霍尔电导

其中↑和↓分别表示自旋向上和自旋向下.

此外,系统的纵向电导[32,33]为

根据纵向电导,可以进一步得到系统自旋极化率

和谷极化率[37]

3 结果与讨论

由于MoS2谷电子对光的手性选择性,使得特定振幅和频率的非共振右旋或左旋圆偏振光只能修饰K谷或K′谷的电子,从而产生能隙的变化,但是此时的能隙不是平衡态布洛赫电子的能隙,而是非平衡态Floquet能隙.图2给出了单层MoS2布里渊区K/K′谷附近自旋依赖的价带与导带子带间能隙随非共振圆偏振光引起的有效耦合能的变化关系.系统布里渊区K谷附近自旋向上、向下价带与导带间的能隙(如图2中正能段黑色实线和红色虚线所示)随着非共振右旋圆偏振光引起的有效耦合能增强呈线性增大,布里渊区K′谷附近自旋向上、向下价带与导带间的能隙(如图2中正能段蓝色点虚线和绿色点线所示)随着非共振右旋圆偏振光引起的耦合能增强先减小后增大,在非共振右旋圆偏振光引起的耦合能0.79和0.87 eV附近自旋向上和向下价带与导带间的能隙减小到趋于0,此时MoS2表现出半金属性.此外,单层MoS2布里渊区K谷附近价带与导带间的能隙随非共振左旋圆偏振光引起的有效耦合能先减小后增大(如图2中负能段黑色实线和红色虚线所示),在非共振左旋圆偏振光引起的耦合能−0.79和−0.87 eV附近发生半导体-半金属相变,K′谷附近自旋向上、向下价带与导带间的能隙(如图2中负能段蓝色点虚线和绿色点线所示)随着非共振左旋圆偏振光引起的有效耦合能增强线性增大.由此可见,外部非共振圆偏振光可引起单层MoS2能带结构有趣的半导体-半金属-半导体转变,从而引起系统自旋/谷输运特性的有趣变化(如图3—图6所示).

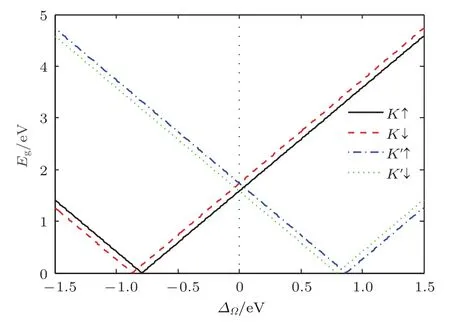
图2 单层MoS2在K/K′谷附近价带与导带间能隙(以eV为单位)随非共振圆偏振光引起的有效耦合能∆Ω的变化关系,其中黑色实线和红色虚线分别表示K谷附近自旋向上和自旋向下价带与导带间的能隙,蓝色点虚线和绿色点线分别表示K′谷附近自旋向上和自旋向下价带与导带间的能隙Fig.2.Energy gap Eg(in units of eV)of the monolayer MoS2as a function of the effective coupling energy∆Ωinduced from the external of f-resonant circularly polarized light where the(black)solid and(red)dashed line demontrates energy gap from the spin-up and-down subbands at the vicinity of K valley,while that for the K′valley is denoted by the(blue)dasheddot and(green)dot line,respectively.

利用久保线性响应理论,进一步研究了非共振圆偏振光作用下单层MoS2的量子化横向霍尔电导.当MoS2费米能级处于价带与导带间的带隙中时,系统自旋/谷依赖的横向霍尔电导趋于量子化[24,32,35].如图3所示,系统横向霍尔电导在非共振右旋、左旋圆偏振光作用下的变化规律类似.下面以单层MoS2在非共振右旋圆偏振光作用下的情形为例展开讨论.当非共振右旋圆偏振光引起的耦合能在0—0.79 eV以及0.87—1.50 eV范围内变化时,如图3所示,单层MoS2布里渊区K谷和K′谷自旋向上量子化霍尔电导分别为e2/2h和−e2/2h;当非共振右旋圆偏振光引起的耦合能在0.79—0.87 eV范围内变化时,K谷自旋向上量子化霍尔电导由e2/2h为−e2/2h、自旋向下量子化霍尔电导仍为e2/2h(如图3(a)中正能段黑色实线和红色虚线所示),K′谷自旋向上横向量子化霍尔电导为−e2/2h、自旋向下量子化霍尔电导由−e2/2h跃变为e2/2h(如图3(b)中正能段蓝色点虚线和绿色点线所示).

图3 单层MoS2横向霍尔电导(以e2/h为单位)随非共振圆偏振光引起的有效耦合能∆Ω的变化关系 (a)黑色实线和红色虚线分别表示K谷附近自旋向上和自旋向下横向霍尔电导;(b)蓝色点虚线和绿色点线分别表示K′谷附近自旋向上和自旋向下横向霍尔电导Fig.3.Transversal Hall conductance σxy(in units of e2/h)of the monolayer MoS2as a function of the effective coupling energy∆Ωinduced from the external of f-resonant circularly polarized light:(a)The(black)solid and(red)dashed line denotes the spin-up and-down transversal Hall conductance at the vicinity of K valley,while that for K′valley in(b)is illustrated by the(blue)dashed-dot and(green)dot line,respectively.

图4 单层MoS2横向量子化自旋霍尔电导(以e2/h为单位)和谷霍尔电导(以e2/h为单位)随非共振圆偏振光引起的有效耦合能∆Ω的变化关系,其中黑色实线和红色虚线分别表示自旋霍尔电导和谷霍尔电导Fig.4.Transversal quantized spin conductance σsxy(in units of e2/h)and σvxy(in units of e2/h)of the monolayer MoS2as a function of the effective coupling energy∆Ωinduced from the external of f-resonant circularly polarized light,as has been denoted by the(black)solid and(red)dashed line,respectively.

图4给出了单层MoS2量子化自旋霍尔电导(黑色实线所示)和谷霍尔电导 (红色虚线所示)随非共振圆偏振光引起的有效耦合能的变化.非共振左旋圆偏振光引起的有效耦合能在−1.50—−0.87 eV范围内变化时,系统量子化自旋霍尔电导为0(如图4中黑色实线所示)、谷霍尔电导为2e2/h(如图4中红色虚线所示).有趣的是,当非共振左旋圆偏振光引起的有效耦合能在−0.87—−0.79 eV范围内变化时,如图4中黑色实线和红色虚线所示,系统自旋霍尔电导为−2e2/h、谷霍尔导由2e2/h跃变为0.当非共振光左电旋圆偏振光引起的有效耦合能在−0.79—0 eV范围内变化时,系统自旋霍尔电导消失、谷霍尔电导从0跃变到2e2/h.此外,如图4中黑色实线所示,当非共振光右旋圆偏振光引起的有效耦合能在0.79—0.87 eV范围内变化时,系统自旋霍尔电导从0—0.79 eV范围内的0跃变到−2e2/h、谷霍尔电导(如图4中红色虚线所示)由2e2/h跃变为0.当非共振光右旋圆偏振光引起的耦合能在0.87—1.50 eV范围内变化时,系统自旋霍尔电导为0、谷霍尔电导(如图4中红色虚线所示)由0跃变到2e2/h.因而,系统量子化自旋霍尔电导和谷霍尔电导[24,35]敏感地依赖于电子的自旋/谷自由度以及外部非共振光偏振光引起的有效耦合能.

进一步研究了单层MoS2纵向电导随非共振圆偏振光引起的有效耦合能的变化关系.如图5中的黑色实线和红色虚线所示,单层MoS2布里渊区K谷附近自旋向上、向下纵向电导在非共振光左旋圆偏振光引起的耦合能−0.79和−0.87 eV附近呈现共振峰(共振峰的能量位置与图2中的半导体-半金属相变能量点以及图3中的K谷横向霍尔电导跃变能量对应).另外,如图5中蓝色点虚线和绿色点线所示,单层MoS2布里渊区K′谷附近自旋向上、向下纵向电导在非共振光右旋圆偏振光引起的耦合能0.79和0.87 eV附近呈现共振峰,共振峰的能量位置与图2中的相变能量点以及图3中的K′谷横向霍尔电导跃变能量一一对应.

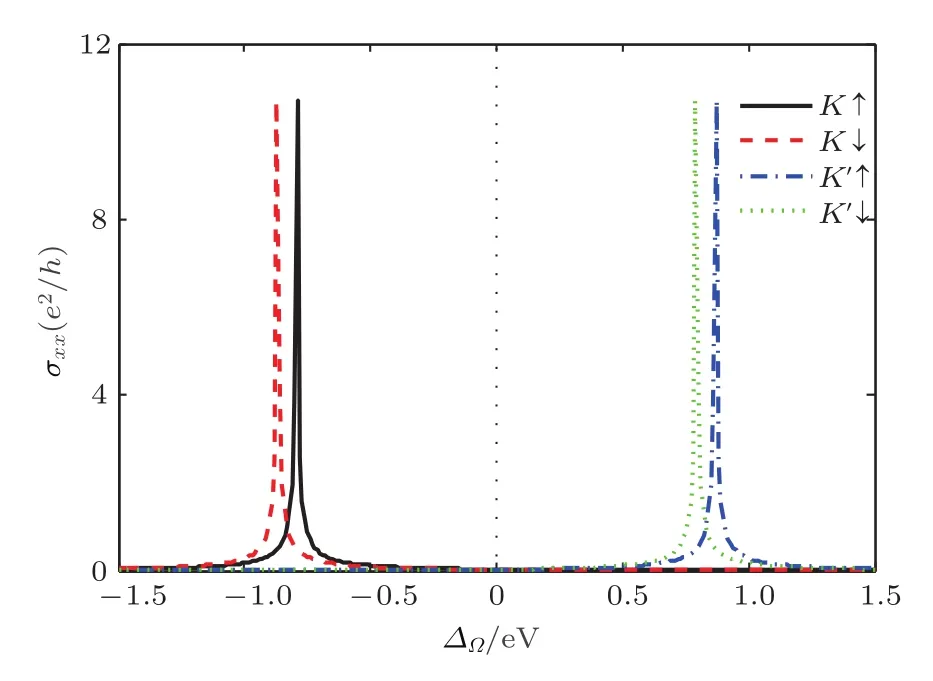
图5 单层MoS2布里渊区K/K′谷附近纵向电导(以e2/h为单位)随非共振圆偏振光引起的耦合能∆Ω的变化关系,其中黑色实线、红色虚线分别表示K谷附近自旋向上、自旋向下纵向电导,蓝色点虚线和绿色点线分别表示K′谷附近自旋向上和自旋向下纵向电导Fig.5. Longitudinal conductance σxx(in units of e2/h)at the vicinity of K/K′valley for monolayer MoS2as a function of the effective coupling energy∆Ωinduced from the external of f-resonant circularly polarized light,where the(black)solid and(red)dashed line denotes the spin-up and-down longitudinal conductance at the vicinity of K valley,while the(blue)dashed-dot and(green)dot line gives the spin-up and-down longitudinal conductance at the vicinity of K′valley,respectively.

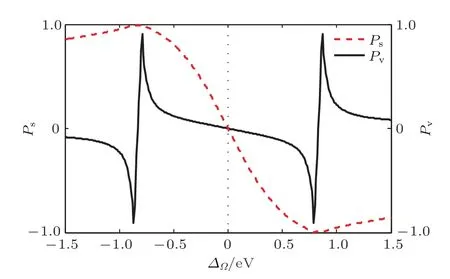
图6 单层MoS2纵向电导自旋极化率Ps和谷极化率Pv随非共振圆偏振光引起的有效耦合能∆Ω的变化关系,其中黑色实线和红色虚线分别表示自旋极化率Ps和谷极化率PvFig.6.Longitudinal conductance spin and valley polarization rate(denoted by Psand Pv,respectively)for monolayer MoS2as a function of the effective coupling energy∆Ωinduced from the external of f-resonant circularly polarized light,as has been illustrated by the(black)solid and(red)dashed line,respectively.

图6给出了单层MoS2自旋极化率和谷极化率随非共振圆偏振光引起的耦合能的变化关系.非共振左旋圆偏振光引起的耦合能在−0.79—0 eV范围内变化时,系统自旋极化率(如图6中负能段黑色实线所示)随着非共振左旋圆偏振光引起的耦合能增强先慢后快增大,在非共振左旋圆偏振光引起的耦合能−0.79 eV附近呈现由正到负的急剧转变,系统谷极化率(如图6中负能段红色虚线所示)先随着非共振左旋圆偏振光引起的耦合能增强先快后慢增大,在非共振左旋圆偏振光有效耦合能−0.87—−0.79 eV范围内达到100%,然后随着非共振圆偏振光有效耦能增强缓慢减小(谷极化率一直保持在90%以上).此外,当非共振右旋圆偏振光引起的耦合能在0—0.79 eV范围内变化时(如图6中正能段黑色实线所示),系统自旋极化率随着非共振右旋圆偏振光引起的耦合能增强先慢后快增强,在非共振右旋圆偏振光引起的耦合能为0.79 eV附近呈现由负到正的急剧转变,系统谷极化率(如图6中正能段红色虚线所示)先随着非共振右旋圆偏振光引起的耦合能增强先快后慢增大,在非共振右旋圆偏振光有效耦合能0.79—0.87 eV范围内达到100%,然后随着非共振圆偏振光引起的有效耦合能增强缓慢减小(谷极化率一直超过90%).可见,利用非共振圆偏振光有望在单层MoS2上实现100%的谷极化,从而用于谷电子器件设计;在特定非共振圆偏振光引起的有效耦合能附近实现系统自旋极化的急速反转,这对基于MoS2的新型高速自旋电子器件设计具有一定的指导意义.

4 结 论

利用紧束缚近似下的低能有效哈密顿模型和久保线性响应理论,研究了外部非共振圆偏振光对单层MoS2电子能带结构、横向霍尔电导、纵向电导及其自旋/谷输运性质的影响.研究结果表明,单层MoS2布里渊区K谷和K′谷附近能隙随着非共振右旋圆偏振光引起的有效耦合能增强分别呈线性增大和先减小后增大,随着非共振左旋圆偏振光引起的有效耦合能增强分别先减小后增大和线性增大,实现有趣的半导体-半金属-半导体转变.此外,非共振圆偏振光有效耦合能绝对值在0.79—0.87 eV范围内变化时,系统自旋霍尔电导为−e2/2h、谷霍尔电导消失.在非共振右/左旋圆偏振光有效耦合能±0.79 eV附近,系统自旋极化率呈现由负到正或由正到负的急剧转变.系统谷极化率随着非共振左旋和右旋圆偏振光有效耦合能增强而增大,在非共振圆偏振光有效耦合能绝对值0.79—0.87 eV范围内接近于100%.总之,外部非共振圆偏振光是调控单层MoS2量子化霍尔电导、自旋/谷霍尔电导以及纵向电导自旋/谷极化的有效手段,可利用外部电磁场实现单层MoS2完全谷极化或自旋极化,为基于低维过渡族金属硫化物的新型高速自旋/谷电子器件设计提供理论基础.

[1]Novoselov K S,Geim A K,Morozov S V,Jiang D,Zhang Y,Dubonos S V,Grigorieva I V,Firsov A A 2004Science306 666

[2]Novoselov K S,Geim A K,Morozov S V,Jiang D,Katsnelson M I 2005Nature438 197

[3]Balog R,Jørgensen B,Nilsson L,Andersen M,Rienks E,Bianchi M,Fanetti M,Laegsgaard E,Baraldi A,Lizzit S,Sljivancanin Z,Besenbacher F,Hammer B,Pedersen T G,Hofmann P,Hornekaer L 2010Nature Mater.9 315

[4]Li X,Wang X,Zhang L,Lee S,Dai H 2008Science319 1229

[5]Zhou S Y,Gweon G H,Fedorov A V,First P N,de Heer W A,Lee D H,Guinea F,Castro Neto A H,Lanzara A 2007Nature Mater.6 770

[6]Xia F,Farmer D B,Lin Y,Avouris P 2010Nano Lett.10 715

[7]Guinea F,Katsnelson M I,Geim A K 2010Nat.Phys.6 30

[8]Chen J H,Jang C,Xiao S,Ishigami M,Fuhrer M S 2008Nat.Nanotechnol.3 206

[9]Li Z,Carbotte J P 2012Phys.Rev.B86 205425

[10]Majidi L,Rostami H,Asgari R 2014Phys.Rev.B89 045413

[11]Splendiani A,Sun L,Zhang Y,Li T,Kim J,Chim C Y,Galli G,Wang F 2010Nano Lett.10 1271

[12]Wang Q H,Kalantar-Zadeh K,Kis A,Coleman J N,Strano M S 2012Nat.Nanotechnol.7 699

[13]Mak K F,Lee C,Hone J,Shan J,Tony F H 2010Phys.Rev.Lett.105 136805

[14]Radisavljevic B,Radenovic A,Brivio J,Giacometti V,Kis A 2011Nat.Nanotechnol.6 147

[15]Liu H,Peide D Y 2012IEEE Electron Dev.Lett.33 546

[16]Zhang Y,Ye J,Matsuhashi Y,Iwasa Y 2012Nano Lett.12 1136

[17]Xiao D,Liu G B,Feng W X,Xu X D,Yao W 2012Phys.Rev.Lett.108 196802

[18]Cao T,Wang G,Han W P,Ye H Q,Zhu C R,Shi J R,Niu Q,Tan P H,Wang E G,Liu B L,Feng J 2012Nat.Commun.3 887

[19]Mak K F,He K,Shan J,Heinz T F 2012Nat.Nanotechnol.7 494

[20]Zeng H,Dai J,Yao W,Xiao D,Cui X 2012Nat.Nanotechnol.7 490

[21]Sengupta P,Bellotti E 2016Appl.Phys.Lett.108 211104

[22]Zheng H L,Yang B S,Wang D D,Han R L,Du X B,Yan Y 2014Appl.Phys.Lett.104 132403

[23]Yarmohammadi M 2017J.Magnet.Magnet.Mater.426 621

[24]Wang S,Wang J 2015Physica B458 22

[25]Yin Z Y,Li H,Li H,Jiang L,Shi Y M,Sun Y H,Lu G,Zhang Q,Chen X D,Zhang H 2012ACS Nano6 74

[26]Rostami H,Moghaddam A G,Asgari R 2013Phys.Rev.B88 085440

[27]Tahir M,Schwingenschlogl U 2014New J.Phys.16 115003

[28]Zhou L,Carbotte J P 2012Phys.Rev.B86 205425

[29]Kitagawa T,Oka T,Brataas A,Fu L,Demler E 2011Phys.Rev.B84 235108

[30]Kitagawa T,Broome M A,Fedrizzi A,Rudner M S,Berg E,Kassal I,Guzik A A,Demler E,White A G 2012Nat.Commun.3 882

[31]Tahir M,Manchon A,Sabeeh K,Schwingenschlogl U 2013Appl.Phys.Lett.102 162412

[32]Sinitsyn N A,Hill J E,Min H,Sinova J,MacDonald A H 2006Phys.Rev.Lett.97 106804

[33]Dutta P,Maiti S K,Karmakar S N 2012J.Appl.Phys.112 044306

[34]Cazalilla M A,Ochoa H,Guinea F 2014Phys.Rev.Lett.113 077201

[35]Tahir M,Manchon A,Schwingenschlogl U 2014Phys.Rev.B90 125438

[36]Feng W X,Yao Y G,Zhu W G,Zhou J J,Yao W,Xiao D 2012Phys.Rev.B86 165108

[37]Missault N,Vasilopoulos P,Vargiamidis V,Peeters F M,van Duppen B 2015Phys.Rev.B92 195423