玻璃-橡胶混合颗粒体系的弹性行为研究∗

赵子渊 李昱君 王富帅 张祺 厚美瑛 李文辉 马钢

1)(太原理工大学力学学院,材料强度与结构冲击山西省重点实验室,太原 030024)

2)(中国科学院物理研究所,软物质物理重点实验室,北京凝聚态物理国家实验室,北京 100190)

3)(太原理工大学机械工程学院,太原 030024)

1 引 言

颗粒物质是大量宏观粒子聚集而成的多体系统.从环绕木星的小行星到沙漠中的沙粒,从南极的浮冰到调味罐里的食盐,日常生活生产中遇到的许多物质都以颗粒的形态而存在.由于粒子之间的碰撞及摩擦,颗粒物质具有典型的强耗散非平衡态体系的特点,与牛顿流体或者弹性固体等连续性介质有显著的区别.在外界扰动下,颗粒物质会在微观-介观-宏观三个空间结构尺度下展现出多个不同特征时间尺度的动力学行为[1−3].对这些行为发生的原理以及机制的认知不仅有助于揭示颗粒材料的基本物理力学特性,而且对于生产及原料运输过程中的能源节约以及山体滑坡等自然灾害的预防有重要现实意义.

玻璃-橡胶颗粒混合材料具有低质量密度、强可压缩性、高阻尼等特点,可应用于廉价路基材料、建筑材料、吸能材料、柔性浮力材料等领域[4−6].弹性模量是材料重要的性能参数,宏观上弹性模量可以衡量物体在外载荷下抵抗弹性变形能力的强弱,微观上弹性模量则是材料单元之间键合强度的指标.调制适当的材料配比可以实现兼顾刚度和柔韧性的二元颗粒混合材料,但材料混合比例对于混合颗粒体系弹性行为的影响以及微观机制尚不明确.李丽华等[7]利用动三轴仪研究颗粒混合土的动力学特性,发现混合土较纯砂土动强度降低而等效阻尼比增加.Lee等[8]研究小粒径橡胶颗粒和大粒径砂土混合材料的动态行为,发现材料表观模量是砂土颗粒含量占比的函数,且函数形式受到样品所处围压状态的影响.陈琼等[9]针对直剪条件下玻璃-橡胶混合体系动力学研究展开,发现随着橡胶颗粒含量的增加,体系会出现剪涨到剪缩的相转变过程,并且伴随着体系弹性的提高.已有研究主要从工程应用角度出发,针对不同应力状态下的样品描述其宏观力学性能的变化,对其微观机制的研究和讨论尚显不足.另一方面颗粒材料是包含多特征时间尺度弛豫效应的复杂材料,其高频动态行为与准静态行为有较大差异,而目前主要实验研究多为准静态加载,缺乏针对混合颗粒材料在高频或者高应变率条件下的动力学行为的系统研究.

利用声速测量来反演材料的弹性模量[10]是材料动态行为研究的常用手段.Jia等[11,12]观察到弹性波在随机密堆颗粒体系中传播时,波形信号由传播速度较快的直接透射相干波和时间较慢但持续时间很长的散射波两部分组成.其中根据直接透射相干波定义的飞行速度由样品宏观动弹性模量决定,并符合基于Hertz-Mindlin接触的等效介质理论(effective medium theory,EMT)描述.近年来陆续有学者[13−18]利用声波探测技术研究单一材料颗粒样品在准静态压缩、直接剪切、三轴剪切等加载条件下的宏观力学特征、耗散机制以及内部结构的演变特征.由于不同材料参数的耦合作用,混合颗粒材料内部颗粒间接触的作用机制以及分布形式更为复杂,进而引起相对单一材料更为独特的弹性行为规律.Taghizadeh等[19]最近的研究声称玻璃-橡胶混合材料的等效弹性模量与橡胶颗粒占比存在非单调关系,令人惊奇的是特定比例下硬玻璃珠和软橡胶珠混合样品的动弹性模量甚至会超过纯玻璃颗粒的动弹性模量.但它们的实验观察结果却与模拟结果大相径庭,对此作者认为此问题仍有待于未来更进一步的研究.有鉴于此,本文通过声学测量和离散元(discrete element method,DEM)模拟方法对玻璃-橡胶混合颗粒的弹性行为变化规律以及发生机制进行研究.测量了混合颗粒体系不同橡胶占比下压缩波波速和等效动弹性模量的变化趋势并从力链结构以及微观接触力分布角度讨论产生该变化趋势的原因;针对不同比例的混合颗粒提出两种改进的等效介质理论模型用于描述混合颗粒体系的波速变化规律.

2 实验方法与结果

2.1 实验方法

实验装置如图1所示.整个装置由样品池、力学加压系统和声波探测系统组成,其中样品池为内径D1=54 mm,高H=90 mm的铝质圆筒;加压装置由压缩实验机和压力传感器组成,压缩实验机型号为智取ZQ-22,压力传感器显示范围0—1000 N,分辨率1 N;声波探测系统由声波发生组件(脉冲信号发生器、发射式压电陶瓷传感器)以及声波探测组件(接收式压电陶瓷传感器、信号放大器、示波器)组成.实验开始前,样品池中通过点源法堆积总计数量为4000颗的玻璃珠和橡胶珠的混合样品,通过游标卡尺测量玻璃珠和橡胶珠的粒径.统计结果显示两种颗粒均为近球形,直径(3.00±0.10)mm.实验选用粒径基本相等的两种颗粒以排除形状和级配对实验结果的影响,并且可以将样品组分体积比用颗粒单元数目比进行表示.实验中以样品所含橡胶颗粒数目占比ξ为标准进行实验,定义为ξ=NR/N×100%,其中NR为橡胶颗粒数目,N为样品颗粒总数目.实验时,首先在混合颗粒样品上表面放置镶嵌压电陶瓷片的活塞作为声波发射传感器;然后将样品池及声波发射传感置于压缩实验机平压头正下方,缓慢转动实验机摇杆向下移动平压头对样品施加法向压力.为排除样品制备过程对实验结果造成的随机性影响,正式测量前先对样品进行三次循环预加载,即每次先对样品加压到600 N持续1 min,至样品表面高度不再发生变化,然后加载到500 N进行正式测量.

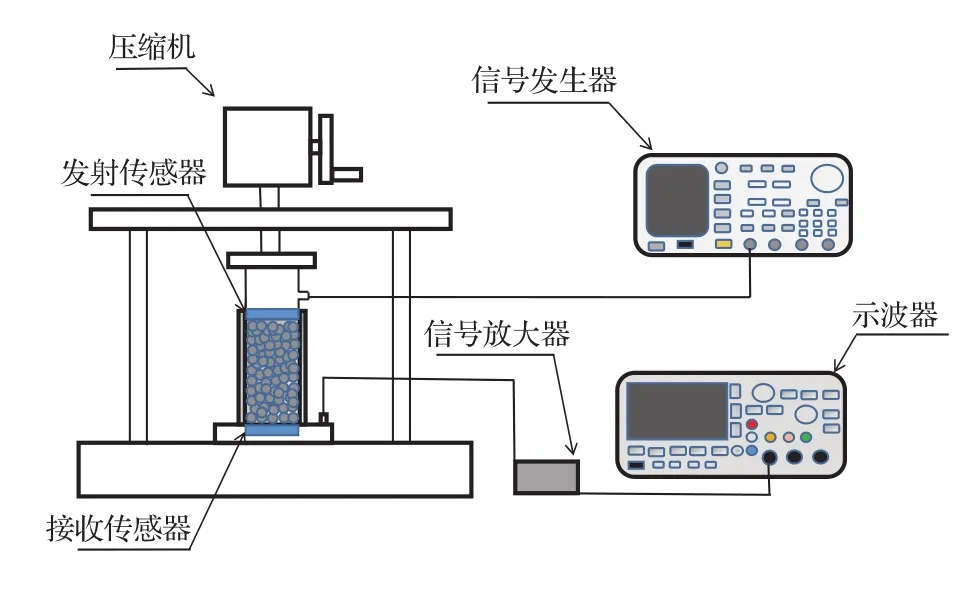
图1 实验装置示意图Fig.1.Sketch of experiment setup.

本文采用飞行时间法测量样品中的声速.实验过程中,信号发生器每隔0.05 s发射一个频率30 kHz的正弦脉冲激励直径50 mm的发生器产生声波,声波穿透颗粒样品后被直径50 mm的接收器接收.发射信号和接收信号由示波器实时记录并存储,如图2所示,其中接收信号在示波器接收前先由信号放大器放大100倍.图2(b)中接收到的信号包括最先到达的E波以及之后强烈的散射波S波.通过测量发射信号和接收信号第一个波形峰值的时间差ttof=t2−t1(其中t1和t2分别代表发射和接收信号前沿时间)和两个传感器之间样品高度H,可以得到E波的传播速度ctof=H/ttof.

图2 实验中发射接收波形 (a)发射脉冲波波形图;(b)接收波波形图Fig.2.Transmitted and received wave in experiment:(a)Transmitted plus wave;(b)received wave.

2.2 实验结果

利用飞行时间法测量了不同材料混合比例颗粒样品的压缩波波速,如图3(a)所示,其中每个数据点重复实验10次计算平均值.可以看到在500 N的法向压力下,实验测量压缩波波速随着橡胶颗粒占比增加呈现非线性单调下降趋势并大致区分为三个阶段.橡胶占比ξ<20%时,压缩波波速基本保持恒定;而在20%<ξ<80%时,波速表现为较快下降过程;ξ>80%时,波速虽然还在减小但是非常缓慢.对于随机堆积颗粒体系,其在外加载荷的束缚下,由于颗粒材料的压缩模量远大于间隙气体的压缩模量,故可忽略间隙气体对声波传播的影响,认为弹性波仅依靠颗粒之间的相互挤压而形成的体系内部力链网络进行传播.钱祖文[20]研究表明如果入射波为平面波,则内部结构散射引起的次级波也为平面波,所以可以利用一维非线性模型等效近似描述实际的三维颗粒介质声波传播及散射过程.根据我们的实验结果,纯玻璃珠样品测量的压缩波波速约为920 m/s,对应的等效波长l∗=v/f约为3 cm,大于10倍颗粒粒径.故在长波长极限近似下,认为混合颗粒材料的等效动弹性模量M∗与介质中的速度VP有关,表示为

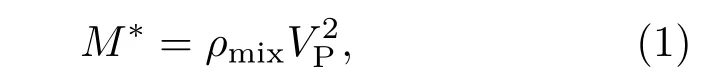
其中ρmix是混合颗粒的密度,由ρmix=(1−ξ)ρg+ξρr给出,ρg和ρr分别是玻璃颗粒和橡胶颗粒的材料密度,ξ是颗粒混合物中橡胶的占比.本实验选用玻璃珠橡胶珠的密度分别为ρg=2.4 g/cm3,ρr=1.2 g/cm3.通过方程(1)计算得到的单轴压缩实验下混合颗粒材料的等效动弹性模量与混合材料比例的关系如图3(b)所示.可以看到M∗呈现一个明显的非线性单调变化,当ξ<20%时,声速基本恒定,主要由于混合颗粒密度的变化导致M∗缓慢减小,视为类玻璃颗粒刚性体系;ξ>80%时M∗缓慢减小,视为类橡胶颗粒柔性体系;而20%<ξ<80%时急剧减小,混合颗粒的力学行为由刚性向柔性过渡.

图3 实验得到压缩波波速和等效动弹性模量与橡胶颗粒占比ξ的关系 (a)压缩波波速随ξ的变化;(b)等效动弹性模量随ξ的变化Fig.3.Compressional wave velocity and dynamic effective elastic modulus versus fraction of rubber particles ξ obtained by experiment:(a)Compressional wave velocity versus ξ;(b)dynamic effective elastic modulus versus ξ.

2.3 模型及参数

为了从颗粒间接触作用及结构几何排布角度更好地理解实验结果,采用基于离散元方法的EDEM软件实现了与上述实验过程类似的计算机模拟.首先构建了直径54 mm、高度90 mm的薄壁圆筒作为容器.在圆筒上表面随机产生球形颗粒掉落到下板上,不同材料比例的玻璃珠与橡胶珠共4000颗均匀下落并等待3—5 s,直至颗粒平均速度小于10−5mm/s.随机生成的颗粒粒径为2.85—3.15 mm.制备好的颗粒样品如图4所示.然后在距样品上表面2 mm的上方生成一块刚性上板,使上板向下运动一定距离将颗粒表面压平,随后向下运动到底板法向受力600 N左右,等待2 s恢复原位置,模仿循环加载过程,3次后上表面高度基本不发生变化.最后待上板运动到底板法向力(扣除颗粒自重)略超过500 N(多为550 N)后静止,待其弛豫到500 N后,使上板完成一个振幅0.001 mm频率30 kHz且持续时间为1.25倍周期的往复运动.这样一个往复运动即模拟实验中压电陶瓷片受电压激励后的振动.应当说明的是,这里上板相较实验的一个周期的脉冲多运动1/4周期,是为了颗粒在经历上板往复运动以及颗粒弛豫过程后,其所受压力与往复运动前基本一致.记录上板与底板的受力曲线以确认压缩波飞行时间,如图5所示.

图4 模拟制备的颗粒样品(图示为橡胶颗粒占比ξ为50%的样品)Fig.4.Prepared particle sample by simulation(sample at fraction of rubber particles ξ=50%).

为了实现计算精度但不过度增加计算量,本文采用Hertz-Mindlin无滑动非线性接触模型[21−23]计算颗粒速度及相互作用力.在半径为R的单个颗粒上的作用力包括重力mg、法向和切向方向接触力Fn和Ft.通过牛顿运动定律表示系统中颗粒i的平动和转动:

式中ri,θi,mi和Ii分别是颗粒i的位置矢量、角位移、质量和惯性矩;是颗粒i的单位角速度;µr,ij是颗粒i和j的滚动摩擦系数.Hertz-Mindlin no-slip模型[21]中颗粒i和j间法向和切向接触力分别为:

这里等效参数分别为颗粒i和j的参数(半径R∗、 质量m∗、 杨氏模量E∗和剪切模量G∗),,和剪切模量;ξi和ξj分别是颗粒i和j的泊松比;β是转换系数定义为;eij表示颗粒i和j的恢复系数;分别表示碰撞时颗粒i和j的相对法向和切向速度,,;δn,ij和δt,ij分别表示颗粒i和j间法向和切向相对位移通过碰撞时计算得到.值得注意的是切向力遵循库仑摩擦定律,最大值为µs,ijFn,ij,这里µs,ij是颗粒i和j间滑动摩擦系数.模拟过程各项材料参数均保持一致,见表1.

图5 模拟发射接收波形 (a)发射脉冲波波形图;(b)接收波波形图Fig.5.Transmitted and received wave in simulation:(a)Transmitted plus wave;(b)received compressional wave.

表1 模拟参数Table 1.Parameters used in simulation.

在DEM模拟中,决定时间步长普遍使用的原理是对于计算颗粒间增加力和位移的时间步长必须小于瑞利临界时间步长∆tr,∆tr可以通过以下计算得到:

这里ρ,ξ和G分别为系统颗粒的密度、泊松比和剪切模量.本文考虑计算时间和计算精度,选择5%∆tr作为计算步长时间实现模拟.

2.4 模拟结果

通过DEM模拟,得到了模拟样品的压缩波声速并求得了等效动弹性模量,每个数据点重复模拟8次.图6为模拟得到的压缩波波速与等效动弹性模量分别随混合组分变化的结果.受实验条件所限,本文实验选用的玻璃珠及橡胶珠的材料参数如剪切模量、泊松比等不能精准确定,故参考前人的相关工作,选用表1所列颗粒材料参数来实现模拟,并主要关注结果变化趋势.可以看到模拟结果与实验结果的趋势基本一致.在橡胶占比ξ<20%以内波速恒定,随后快速下降,ξ>80%后声速缓慢减小.等效动弹性模量随着ξ的增加也呈现出单调非线性下降.下文对于混合颗粒体系表现出的非线性行为,通过力链结构与微观单元接触力的分布进行分析.

图6 模拟得到压缩波波速和等效动弹性模量同橡胶颗粒占比ξ的关系与实验结果的对比 (a)压缩波波速随ξ变化的模拟与实验结果;(b)等效动弹性模量随ξ变化的模拟与实验结果Fig.6.Comparison of the results between simulation and experiment:(a)Comparison of compressional wave velocity versus ξ by DEM simulations and experiment;(b)comparison of dynamic effective elastic modulus versus ξ by DEM simulations and experiment.

3 讨 论

颗粒材料通过颗粒间相互接触产生的独特的力链网络结构来承受外界载荷.光弹实验[24]显示,力链网络上局部颗粒间接触有强弱之分,传递较大份额荷载的路径构成强力链,反之形成弱力链.尽管强力链颗粒间平均作用力远大于弱力链颗粒间平均作用力,但弱力链所包含的颗粒数目却远大于强力链,正是力链结构的这种二重性决定了样品的宏观力学性质.对于我们的实验结果,当ξ<20%时样品压缩波波速基本恒定,考虑到接收到的声波信号中最先到达的是通过强力链传播而来的直接透射相干波,这也暗示混入少量的橡胶颗粒在统计意义上并没有改变样品中力链的结构特征.选取模拟样品轴对称剖面处厚度为4 mm(略大于1倍粒径)的切片,统计切片内部出现的颗粒间法向的相互作用力并将大于平均值的法向力矢量用绿色标记,接触力越大则力矢量越粗.由此得到不同橡胶颗粒占比时样品内部的力链结构,如图7所示.结果显示当ξ=10%以及ξ=20%时,只有极个别的橡胶珠参与了主力链的构成,可视为橡胶珠仅仅填充在主力链周围的空位.样品仍然是由玻璃颗粒也就是硬颗粒所组成的主力链来承担外载荷.类似于光学费马原理,相干波沿着更快的主力链传播,这就导致低橡胶占比样品压缩波波速基本恒定的特征.当ξ>20%以后,随着混合颗粒体系中橡胶占比增加,橡胶颗粒逐渐取代主力链上的玻璃颗粒,压缩波通过主力链上更软的橡胶珠也就需要花费更多的时间,所以声速以及等效动弹性模量持续减小.对于ξ>80%的样品,由于橡胶珠模量较低,每个单元都会有比玻璃单元更大的变形,其内部力链分布相对更加均匀,参与主力链的颗粒数目会更多,此时少量的玻璃颗粒可视为悬浮于橡胶颗粒中,此范围内玻璃珠含量对声速的影响有限.

考虑到图7只统计了一个切片上的力链分布,为了得到更可靠的结论,我们统计了样品内部所有颗粒间的接触力的概率密度函数,用于描述样品内部力的分布特征,如图8所示.其中颗粒间的接触类型按三种不同情况统计:g-g,g-r,r-r(其中g代表玻璃颗粒,r代表橡胶颗粒).结果显示:对于ξ=10%及ξ=20%的样品,g-g型接触力分布形式同ξ=0%的样品基本相同,且该类型接触力为样品内部接触力的主要形式,并为样品提供强接触力从而形成承受外界载荷的强力链结构.相对而言g-r型与r-r型接触力不仅数量少,产生强力的概率也小于g-g型接触,尤其是r-r型接触基本不包含大于平均力的接触,以上结果与单一切片内部力链图的观察结果是相同的.对于ξ=50%的样品,三种类型的接触力分布基本一致,可见无论是橡胶颗粒还是玻璃颗粒都参与了强力链的组成.当ξ进一步增大到80%以上,g-g型接触数目急剧减小,并且主要以弱接触形式存在,且样品内部大于5倍平均力的强力出现概率小于低橡胶颗粒占比样品,可以认为高橡胶颗粒占比样品内部力的分布相对更为均匀.

文献[19]报道了相似的实验,但他们的结果显示当橡胶珠含量ξ≈20%的样品等效动弹性模量甚至超过纯玻璃珠样品,对于这个结果作者也没有给出明确的解释.我们查阅的其他文献所报道的各实验条件下的弹性模量结果均是随着橡胶颗粒增加而减少.但文献[19]与本文结果一致的是玻璃-橡胶混合颗粒样品均表现为从类玻璃的刚性行为转变为类橡胶的柔性行为的非线性变化.这种变化趋势和多相均匀连续介质的声速测量结果十分类似.已有工作[25,26]证明多相均匀连续介质的声速测量结果介于两个极限之间,即:基于等应变假设的Viogt上限和等应力假设的Reuss下限.这种相似性意味着混合颗粒内部声传播也可能存在两种不同的机制.对于单种颗粒材料,EMT能够较好地描述满足紧束缚及仿射变换近似颗粒体系的弹性波行为.对于二元混合颗粒材料尚缺乏相关模型,这里我们简单讨论EMT对混合颗粒样品的适用性.EMT从颗粒间的Hertz接触模型出发,基于平均场理论的思想,建立起单一介质颗粒固体力学量和声速之间的关系.压缩波波速满足

其中K为体积模量,µ为剪切模量,ρ∗为样品等效密度.K,µ又分别记为:

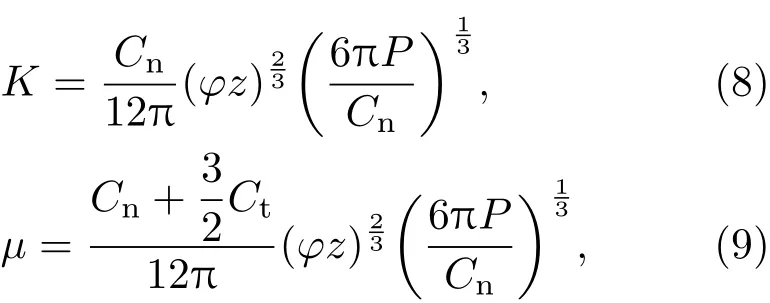
其中Cn为法向刚度,Ct为切向刚度,φ为体积分数,z为平均配位数.

由于颗粒间无论是哪种材料的相互接触都认为满足Hertz关系,即认为球与球之间通过非线性弹簧链接.则将混合颗粒样品整体作为质点-弹簧复杂网络体系.上文已经说明在ξ<20%时主要由玻璃珠构成主力链结构,考虑到玻璃珠的模量远大于橡胶珠,则此时样品内部颗粒间的变形较接触力的分布更为均匀,近似满足等应变假设,类比于振动力学多弹簧连接等效刚度的思想,认为混合颗粒样品可以简化为并联弹簧模型.反之当ξ>80%时,橡胶珠变形较大,但颗粒间作用力分布相对均匀,如图8(e)和图8(f)所示,故可将混合颗粒简化为串联弹簧模型.对于混合颗粒,推导其EMT严谨的解析形式十分困难,这里进行一个近似化处理.假设样品的串联等效刚度为:

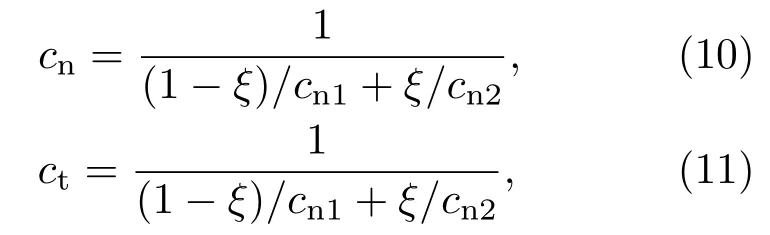
并联等效刚度为

将不同材料比例调制的等效刚度代入(7)—(9)式即可得到两种改进EMT模型的计算结果.

图7 不同ξ时样品内部的力链图(图中粉红色颗粒为玻璃珠,黄色颗粒为橡胶珠,绿色矢量为颗粒间大于平均法向力的力矢量,线越粗代表力矢量越大)Fig.7.The force chain diagram of the samples at different ξ(the pink particles are glass beads and the yellow particles are rubber beads,the green vector is force vector larger than average normal force between the particles,the thicker line represent the larger force).

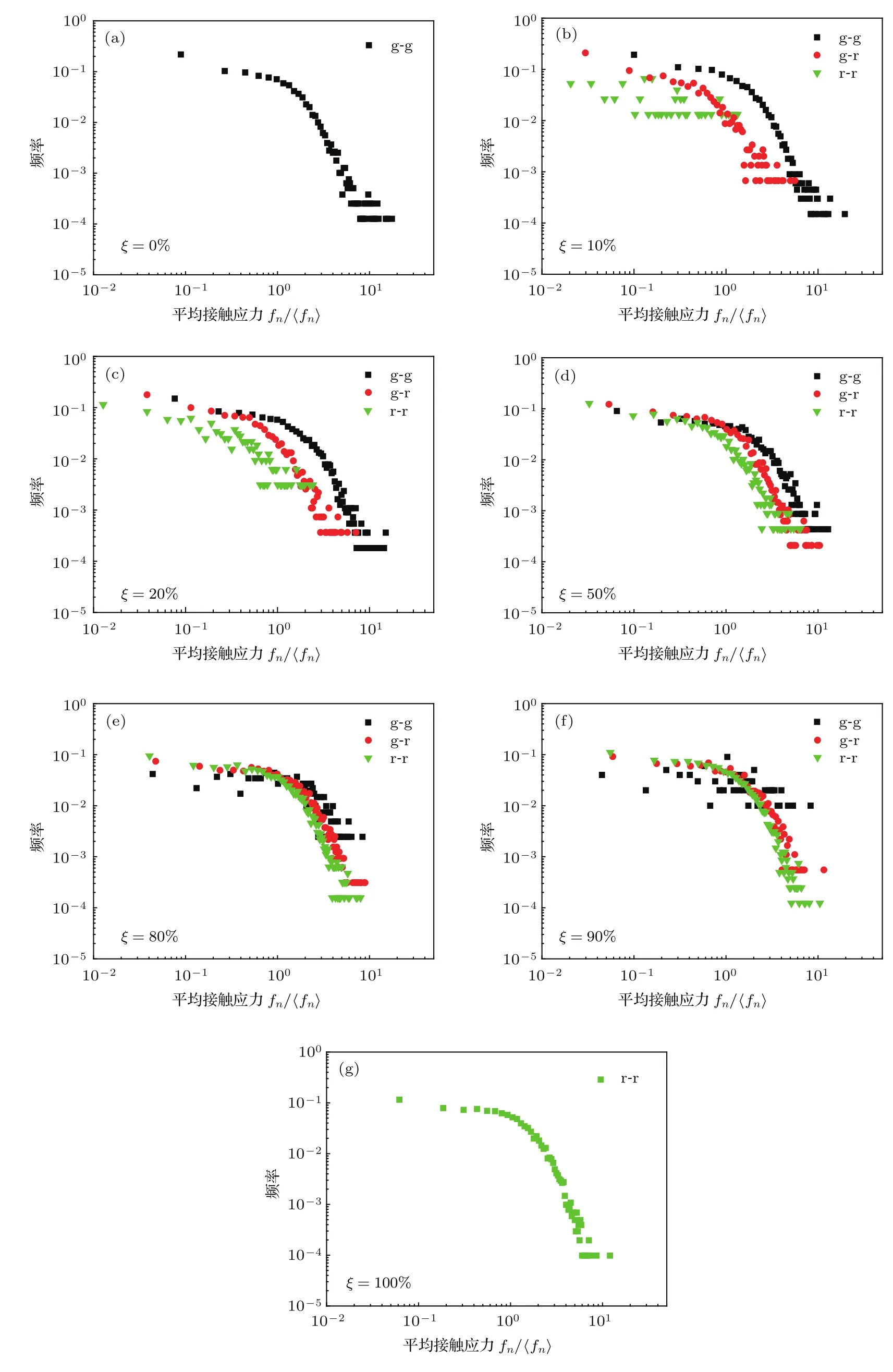
图8 不同ξ时颗粒间法向接触力的概率密度函数 (g代表玻璃珠,r代表橡胶珠,(a)—(g)分别代表ξ=0%,10%,20%,50%,80%,90%和100%)Fig.8.The probability density function of the normal contact force between the particles at different ξ(g stands for glass beads,r stands for rubber beads,Figures(a)–(g)stands for ξ =0%,10%,20%,50%,80%,90%and 100%).

图9 改进等效介质理论模型声速计算结果和模拟结果(黑色点表示并联弹簧假设下等效介质理论计算结果,红色点表示串联弹簧假设下等效介质理论计算结果,绿色点为模拟结果,上述结果均进行了归一化处理)Fig.9.Sound velocity calculated by improved effective medium theory and simulation results(the black dots show the calculation results of improved effective medium theory based on parallel spring hypothesis,the red dots represent the results of improved effective medium theory based on series spring hypothesis,and the green dots is the simulation results.All the above results are normalized).

由于实验无法得到内部接触配位数的值,故选择将模拟数据与按照并联模型及串联模型计算得到的数据作为对比.统计模拟结果平均配位数时,对于接触边壁的颗粒(约有1000个左右)只统计颗粒间的接触,故造成统计实际值较理想值偏低,本文配位数变化范围为4.37—5.58.模拟结果及模型结果进行归一化处理如图9所示.显然按照并联模型改进的EMT计算结果与橡胶占比较低时模拟结果相符合,而按照串联模型改进的EMT计算结果与橡胶占比较高时模拟结果一致.其他橡胶颗粒占比下模拟结果与两个模型计算的结果均存在较大偏差.对于文献[19]所报道的结果与本文结果的差异,可能是因为本文采用固定刚性边壁容器加载,而文献[19]采用偏应力为零的静水压加载方式加载,从而两个实验样品内部的应力状态不同所致.下一步我们计划就边界条件以及加载方式对于混合颗粒弹性的影响等问题展开研究.

4 结 论

本文利用声波探测的实验方法结合离散元模拟,研究了随机密堆玻璃-橡胶混合颗粒体系所含材料比例与体系等效动弹性模量的关系.实验和模拟结果显示,随着橡胶珠掺杂比例的增加,混合体系的等效动弹性模量呈现出非线性单调变化.当ξ<20%时,模量降低趋势比较缓和,表现为类玻璃颗粒刚性行为;随后模量迅速降低,直至ξ>80%,变化趋势再度缓和,表现为类橡胶颗粒柔性行为.通过样品内部力链与接触力分布的分析,认为低橡胶占比的混合样品内主要是由玻璃珠构成承载外力的主力链而橡胶珠基本不参与.进入转换区后橡胶珠代替玻璃珠出现在主力链上,因此声波传播更慢,体系逐渐向类橡胶柔性区转化并在高橡胶占比时再次稳定.对于低橡胶占比和高橡胶占比的样品提出了基于等效并联模型和串联模型的改进EMT形式,理论计算结果和模拟结果相符合.该研究有利于人们更为直观地了解混合颗粒材料弹性行为的变化规律,并对材料力学性能优化以及实际应用有一定的理论指导作用.

感谢山西省“1331工程”重点创新团队项目对课题的资助.

[1]Jaeger H M,Nagel S R,Behringer R P 1996Rev.Mod.Phys.68 1259

[2]Liu C Q,Sun Q C,Wang G Q 2014Mech.Engineer.36 716(in Chinese)[刘传奇,孙其诚,王光谦 2014力学与实践36 716]

[3]Kou B Q,Cao Y X,Li J D,Xia C J,Li Z F,Dong H P,Zhang A,Zhang J,Kob W,Wang Y J 2017Nature551 360

[4]Wang S M,Gao Y F 2007Rock and Soil Mechanics28 1001(in Chinese)[王庶懋,高玉峰2007岩土力学28 1001]

[5]Chen Y N,Xiao J M 2015Chin.J.Engineer.37 1498(in Chinese)[陈亚楠,肖久梅2015工程科学学报37 1498]

[6]Liu W X,Wu P W,Dai J H 2017Develop.Appl.Mater.32 27(in Chinese)[柳文鑫,吴平伟,戴金辉 2017材料开发与应用32 27]

[7]Li L H,Xiao H L,Tang H M,Hu Q Z,Sun M J,Sun L 2014Rock and Soil Mechanics35 359(in Chinese)[李丽华,肖衡林,唐辉明,胡其志,孙淼军,孙龙 2014岩土力学35 359]

[8]Lee J S,Dodds J,Santamarina J C 2007J.Mater.Civil Engineer.19 179

[9]Chen Q,Wang Q H,Zhao C,Zhang Q,Hou M Y 2015Acta Phys.Sin.64 154502(in Chinese)[陈琼,王青花,赵闯,张祺,厚美瑛2015物理学报64 154502]

[10]Qian Z W 1993Appl.Acoust.12 1(in Chinese)[钱祖文1993应用声学12 1]

[11]Jia X P,Caroli C,Velicky B 1999Phys.Rev.Lett.82 1863

[12]Jia X P 2004Phys.Rev.Lett.93 154303

[13]Zhang P,Zhao X D,Zhang G H,Zhang Q,Sun Q C,Hou Z J,Dong J J 2016Acta Phys.Sin.65 024501(in Chinese)[张攀,赵雪丹,张国华,张祺,孙其诚,侯志坚,董军军2016物理学报65 024501]

[14]Zheng H P,Jiang Y M,Peng Z,Fu L P 2012Acta Phys.Sin.61 214502(in Chinese)[郑鹤鹏,蒋亦民,彭政,符力平2012物理学报61 214502]

[15]Zhang Q,Li Y,Hou M,Jiang Y,Liu M 2012Phys.Rev.E85 031306

[16]Zhou Z G,Zong J,Wang W G,Hou M Y 2017Acta Phys.Sin.66 154502(in Chinese)[周志刚,宗谨,王文广,厚美瑛2017物理学报66 154502]

[17]Khidas Y,Jia X P 2012Phys.Rev.E:Stat.Nonlin.Soft Matter Phys.85 051302

[18]Liu X Y,Jiao T F,Ma L,Su J Y,Chen W Z,Sun Q C,Huang D C 2017Granular Matter19 55

[19]Taghizadeh K,Steeb H,Magnanimo V,Luding S 2017Powders&GrainsMontpellier,France,July 3–7 2017 p12019

[20]Qian Z W 2012Acta Phys.Sin.61 134301(in Chinese)[钱祖文 2012物理学报61 134301]

[21]Di Renzo A,Di Maio F P 2004Chem.Engineer.Sci.59 525

[22]Han Y L,Jia F G,Tang Y R,Liu Y,Zhang Q 2014Acta Phys.Sin.63 174501(in Chinese)[韩燕龙,贾富国,唐玉荣,刘扬,张强2014物理学报63 174501]

[23]Chen H,Liu Y L,Zhao X Q,Xiao Y G,Liu Y 2015Powder Technol.283 607

[24]Snoeijer J H,Vlugt T J,van Hecke M,van Saarloos W 2004Phys.Rev.Lett.92 054302

[25]Hashin Z,Shtrikman S 1963J.Mech.Phys.Solids11 127

[26]Yang X S,Ma J,Liu L Q 2004Seismol.Geol.26 484(in Chinese)[杨晓松,马瑾,刘力强 2004地震地质 26 484]