基于双折射晶体的快拍穆勒矩阵成像测偏原理分析∗

曹奇志元昌安胡宝清任文艺赵银军张晶李建映 邓婷 Mingwu Jin

1)(广西师范学院物理与电子工程学院,南宁 530023)

2)(广西师范学院北部湾环境演变与资源利用教育部重点实验室,广西地表过程与智能模拟重点实验室,南宁 530023)

3)(西北农林科技大学理学院,杨凌 712100)

4)(Department of Physics,University of Texas at Arlington,Arlington,TX 76019,USA)

5)(Department of Electrical and Computer Engineering,University of Delaware,Newark,DE 19716,USA)

1 引 言

偏振成像技术是利用光电成像器件获取目标景物辐射的偏振信息,不仅可获得目标光学辐射的光强度信息,而且可获得目标的偏振信息,显著增加被探测目标场景的信息量[1−3].目标的偏振信息与其自身的介电常数、粗糙度、组织结构、含水量等有密切关系[4].穆勒矩阵是一种应用广泛的偏振表征量,能够全面反映目标的偏振光学特性.它是一个4×4的矩阵,共16个阵元.穆勒矩阵成像测偏技术(Mueller matrix imaging polarimeter,MMIP)是一种能完全表征目标偏振属性的偏振成像技术[5,6],是当今偏振成像领域研究的热点之一[5−17].

穆勒矩阵成像测偏技术具有光学成像非侵入、无辐射、无损伤等优点,按照调制方式不同,可分为分时型和快拍型[10,18].分时型一般包含有机械转动(如旋转玻片等)[19−21]或相位延迟调制(如液晶等)[22−34]部件,其偏振态产生部分(PSG)和分析部分(PSA)都是沿着时间轴调制.分时型穆勒矩阵成像测偏仪虽然原理简单,获得的偏振图像空间分辨率高,但系统中含有活动部件和需要多次测量,这限制了其测量精度和应用范围[25].

快拍(snapshot,也有学者称为同时或快照式)穆勒矩阵成像测偏技术(SMMIP)是采用不同的空间载频将目标的全部偏振信息调制到一帧干涉图中,通过一次曝光获取目标的全部16个穆勒矩阵阵元图像[12,25],其测量速度最快[12,25].SMMIP是在空间调制快拍斯托克斯(Stokes)成像测偏技术上发展起来的[35].空间调制快拍斯托克斯成像测偏技术是采用不同的载频将目标的全部4个斯托克斯参量(S0,S1,S2和S3)调制到一帧干涉图中,通过一次曝光获取目标全部斯托克斯参量[35−40].它按核心调制器件可分为偏振光栅型[35]和双折射型(包括楔形棱镜[36]、萨瓦偏光镜[37,38]和改进型萨瓦偏光镜(modified savart polariscopes,MSP)[39−41]).2015年,Wang等[12]和Kudenov等[25,35]开展了以偏振光栅为核心调制器件的SMMIP研究,并展示了其在眼部疾病(青光眼)早期诊断方面的潜在应用价值,但获取目标的穆勒矩阵图像空间分辨率较低;具有高消光比的双折射晶体备受空间调制快拍斯托克斯成像测偏技术研究者们的青睐[26−41],并且已有研究表明以MSP为核心调制器件的技术方案在通道宽度、空间分辨率、信噪比和视场等方面具有显著优势[39,40].本文主要对以MSP为核心调制器件的SMMIP的基本原理进行分析.

2 光路设计与测量原理

图1是MSP-SMMIP光学设计示意图,它包含一个偏振态产生部分和一个偏振态分析部分,主要包括光源(source),准直透镜(f1),起偏器(P1),改进型萨瓦偏光镜(MSP1),半波片(HWP1),MSP2,成像镜(f2),被测样品(sample),准直透镜(f3),MSP3,HWP2,MSP4,检偏器(P2),二次成像镜(f4)及焦平面阵列(FPA).其中MSP-SMMIP系统中核心分光器件是MSP,可以将其看成两块萨瓦板(SP)夹一个半波片的“三明治”结构,其中MSP3和MSP4的SP厚度相等,它们是MSP1和MSP2的SP厚度的两倍.准单色光源Source发出光束经过f1准直后,入射到起偏器P1上,经过P1的透射光可以表示成入射光的归一化斯托克斯参量形式,Sin=(S0,in(x,y)/2)[1 0 1 0]T,上标T代表矩阵中的转置,S0,in(x,y)是入射光的总光强.透射光经过MSP1,HWP1和MSP2后分成四束光,这些光线经过成像镜f2后,形成干涉条纹定位在样品上.这些条纹通过两种载频调制样品的穆勒矩阵M(x,y),被调制后的光场通过f3准直进入到偏振态分析模块中.从偏振态产生模块中出来的四束光,经过MSP3,HWP2和MSP4后分成16束光.最后,这16束光线经过检偏器P2和二次成像镜f4干涉、成像于焦平面阵列FPA上.

图1 MSP-SMMIP光学设计示意图 起偏器P1和检偏器P2的偏振化方向为45◦,半波片HWP1和HWP2的快轴方向为22.5◦,改进型萨瓦偏光镜MSP1和MSP3沿着y轴方向剪切,MSP2和MSP4沿着x轴方向剪切,MSP3和MSP4的SP单板厚度是MSP1和MSP2的两倍Fig.1.Optical layout of MSP-SMMIP,P1and P2are linear polarizers at 45◦,half wave-plates,HWP1and HWP2have fast axes oriented at 22.5◦.MSP1and MSP3shear the beam along x while MSP2and MSP4shear along y.The single SP’s thickness of the generator’s and analyzer’s MSP are t and 2t,respectively.

利用斯托克斯矢量-穆勒矩阵(Stokes vector-Mueller matrix)形式[6],可以方便地研究空间调制稳态快拍穆勒矩阵成像测偏系统的探测原理.设入射光的Stokes参量为S0,in(x,y),用一个4×1的矩阵表示.出射光的Stokes参量S0,out(x,y)等于光学系统的Mueller矩阵M乘以入射光的Stokes参量S0,in(x,y),即S0,out(x,y)=MS0,in(x,y).基于本测量系统的基本结构和探测原理,设f1=f2=f3=f4时,入射光经过系统的矩阵传输方程可表示为

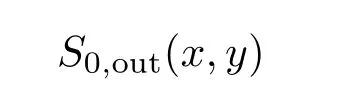
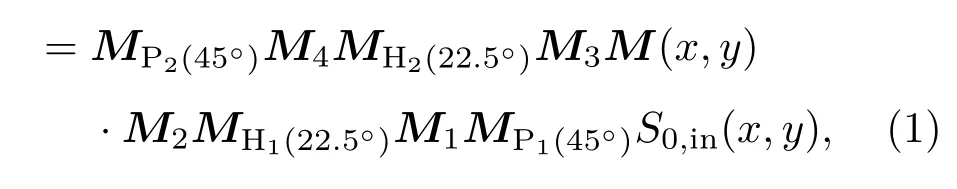
其中,MP2(45◦),M4,MH2(22.5◦),M3,M(x,y),M2,MH1(22.5◦),M1 和MP1(45◦)分别表示检偏器P2、改进型萨瓦偏光镜MSP4、半波片HWP2、改进型萨瓦偏光镜MSP3、样品、改进型萨瓦偏光镜MSP2、半波片HWP1、改进型萨瓦偏光镜MSP1和起偏器P1的Mueller矩阵[6].

通过计算(1)式,可得到焦平面FPA上光强I(x,y)=S0,out(x,y):

其中k=2πΩ,Ω=∆/(λf)是空间载频,λ是入射光的波长,f是成像镜的焦距,∆是萨瓦偏光镜单板横向剪切量[39].为了重构样品的Mueller矩阵阵元mij(下标i和j是4×4的Mueller矩阵的行和列),需对干涉图I(x,y)进行傅里叶变换将其转换到频域I′(x,y)(如图2所示),可以看出该图中有33个分离的峰(通道),这些通道复系数Sn分别包含样品Mueller矩阵不同阵元信息(见表1).

为解调出这些Mueller矩阵阵元,需要采用二维滤波器对相应通道进行滤波.当某个k通道被滤波,再对该通道进行反傅里叶变换获得Ck,它包含复系数Sn和调制相位因子.为了解调出Sn,需要一个或者多个已知Mueller矩阵Mr作为参考数据去定标每个通道的调制相位因子[6,8].

(3)式中Csk和Crk分别是样品和参考数据的第k通道数据.此外,Cs0和Cr0是用来消去光源对样品测试结果的影响.求解各Mueller矩阵分量的等式见表2.

表1 每个通道复系数Sn(包含样品被编码到干涉图中的Mueller矩阵阵元)Table 1.The complex coefficients Snof each channel(including the Mueller matrix elements encoded in the interferogram).

表2 从频域中求解Mueller矩阵分量Table 2.Resolved Muller matrix elements mijfrom the Fourier domain.

图2 干涉图频谱,包含33个通道Fig.2.Fourier spectra of interferogram.It includes 33 channels.

3 光学指标

以上对MSP-SMMIP的工作原理和特性进行了分析,下面将以特定的面阵探测器来分析设计系统的性能参数.面阵探测器对空间调制快拍穆勒矩阵测偏仪的性能起着决定性作用,其帧频决定快拍测量速度,其分辨率是决定测偏仪的空间分辨率的重要因素.由于MSP-SMMIP空间通道数达到33个,为了使得每个通道容纳的信息尽可能多,必须充分利用面阵探测器的整个探测面阵,以获得最大的空间分辨率.因此,应以可获得的面阵探测器来制定相关技术指标.本文以加拿大DALSA公司生产的Pantera TF 1M60为例制定指标.CCD的参数:空间分辨率为1024×1024,像元大小为12µm×12µm,最高帧频可达60帧/s.

由于 CCD上沿y方向的一行像元数为N=1024,且相邻像元间距为a=12µm.由图3可知,在频域中,沿着y方向需分成7个通道,每个通道频域宽度等于空间载频Ω,为了尽可能地利用探测器阵列全部阵元,每个通道空域宽度为L=1/Ω=Na/7≈1.755 mm,则载频Ω=1/L=0.57 mm−1. 在频域中,如果采用矩形滤波器滤波,则滤波器截止频率为Ωc=Ω/2=0.285 mm−1.系统的空间分辨率由系统的放大倍数和像元大小共同决定ε=7a/Q,其中a为像素尺寸,Q为光学系统的总放大倍率,乘以7是因为整个探测器阵面沿着y(和x)方向分成了7个通道.可见快拍穆勒矩阵成像测偏仪测量速度提高16倍是以空间分辨率降低7倍为代价的.若系统的总放大倍率为Q=1,空间分辨率就为ε=84µm.上述系统指标确定以后,由于Ω=∆/λf,λ是入射光的波长,f是成像镜的焦距,∆是萨瓦偏光镜单板横向剪切量.因此可根据这些指标来设计关键光学元器件的参数:如改进型萨瓦偏光镜的厚度;物镜、准直透镜和成像镜的焦距等.

4 数值模拟

参考上节光学指标,基于MATLAB软件平台,进行模拟实验,除对模拟结果进行视觉定性评估,也采用相关系数(correlation coefficients,CC)和峰值信噪比(peak signal to noise ratio,PSNR)进行定量评估.

4.1 模拟及其定性分析

图3(a)为输入系统的Mueller矩阵目标图像,该图像十分有趣,图像中心的空间频率明显高于边缘,其中部分图像尤为明显(如m33等).图4是基于(2)式模拟得到的干涉图,从图中可以看到清晰的干涉条纹.图4的傅里叶变换谱见图2,可以看出该图中有33个分离的峰(通道),这表明模拟的图像中包含了相应的载频.同时这33个峰(通道)分别包含着输入Mueller矩阵16个阵元的信息,如果要解调出这些Mueller矩阵阵元,需要对相应通道采用二维滤波器进行滤波,再进行二维反傅里叶变换.为了消去调制相位因子,需要对每个通道进行定标,被用于定标的参考目标必须确保每个通道的定标数据不为零.MSP-SMMIP光学系统,只需要偏振化方向为22.5◦的线性偏振片作为参考目标,一次即可将33个通道全部定标.相比文献[25],采用多器件多角度的多次定标,MSP-SMMIP定标更加简洁高效,两者差异主要是因为两种光学系统采用的核心分光器件不同,分光机理也不同,对偏振态的调制结果不同.图3(b)为反演出的Mueller矩阵图像,该图很好地反演出了输入Mueller矩阵图像的低频信息(如m12).图3(b)部分分量(如m33)中心部分模糊,由第4节光学指标计算中可知,这主要是部分目标高频信息超出了低通滤波器的截止频率,而采用频域反演技术时,低通滤波器会截断超出截止频域的高频信息部分.这样会导致高频信息在滤波过程中丢失,而高频信息对应的是目标空间频率高的部分,即目标的细节(如m33的中心部分),目标细节信息丢失会导致目标图像中心高频部分模糊.需要特别指出的是,图3是伪彩色图像,其颜色表示该数值大小,具体颜色代表那个数值可查看图3下部的颜色条.

图3 (a)模拟输入目标图像;(b)测量结果图像Fig.3.(a)Simulated input;(b)simulated measurement.

图4 MSP-SMMIP模拟干涉图Fig.4.Simulated image of MSP-SMMIP.

4.2 反演图像质量定量评价

相关系数CC和PSNR可以较好地从图像的相关性和绝对误差两方面评价图像的重构质量.首先采用相似性评估的方法来评价反演图像和输入目标图像的相似性.相似性测量主要是计算两者的CC(其值范围在0—1之间),CC越高表明这两幅图像越相似,也就是该反演图像与输入目标图像越相似,重构得越好.图5所示为反演图像与输入目标图像的CC,可以看出,CC均在0.82以上,表明反演图像与输入图像之间存在强相关,亦表明获得了非常好的测量结果.

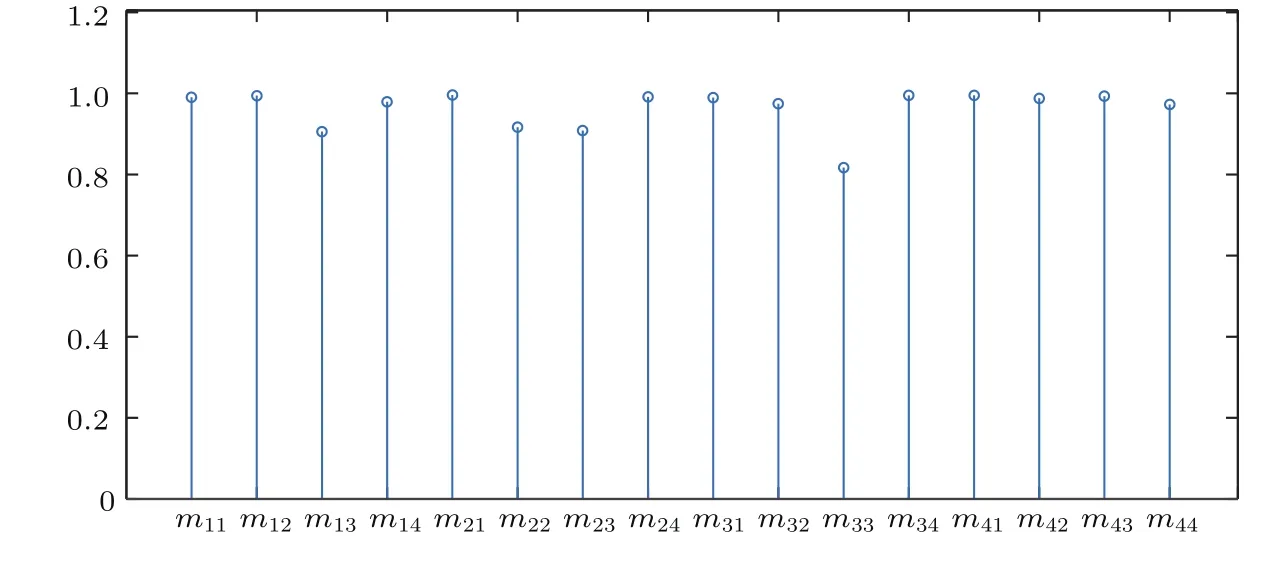
图5 反演图像与输入目标图像的CCFig.5.The correlation coefficients between reconstructed image and input image.

图6 峰值信噪比Fig.6.Peak signal to noise ratio.

PSNR经常用作图像重建质量评价.PSNR表示信号最大可能功率和影响它的表示精度的破坏性噪声功率的比值,由于许多信号都有非常宽的动态范围,峰值信噪比常用对数分贝单位来表示.一般来说,PSNR值越大,重构质量越好,绝对误差越小.图6是反演穆勒矩阵每个阵元的PSNR,从图中可知,单独占有一个通道的穆勒矩阵阵元(如m12和m21)的PSNR比多个穆勒矩阵阵元(如m24和m42)共享一个通道高.此外,从图中可知PSNR均在23以上,这表明测量结果绝对误差较小.

在此需特别指出,本文主要聚焦于介绍MSPSMMIP探测的新原理和系统的光学指标初步设计,给出基于理想情况下的理论分析和数值模拟结果.相应的实验室原理验证实验、定标实验和定量分析等将在未来的工作中呈现.

5 结 论

提出了一种以改进型萨瓦偏光镜为核心器件的空间调制稳态快拍穆勒矩阵成像测偏新技术,它采用不同的空间载频将16个穆勒矩阵阵元调制到一幅干涉图中,能实现一次曝光获取目标图像和全部穆勒矩阵阵元图像.采用斯托克斯矢量-穆勒矩阵形式阐明MSP-SMMIP的探测原理,研究了Mueller矩阵重构和系列定标技术,分析了系统的光学指标,采用计算机仿真实验验证了MSPSMMIP原理方案的正确性.对仿真结果的主观和客观评价表明模拟测量结果较好.与分时型相比,该技术的优势在于:1)测量系统无运动部件,结构紧凑,体积小,系统的可靠性和稳定性好;2)测量系统不受探测目标和系统自身相互运动以及外界环境扰动的影响,偏振探测精度高;3)探测系统通过一次测量即可获取探测目标的全部偏振特性,探测速度快,可以用于静、动态目标和动态场景的探测.所以,该技术可极大地满足生物医学(如眼部疾病)、遥感(如动态目标识别)和工业(如流水线质量监控)等领域对活体、运动目标或动态场景同时和实时快速检测的实际需求.然而,现有频域反演技术的局限性导致Mueller矩阵阵元重构过程中目标高频信息丢失,高频信息对应着目标的细节,这导致该技术暂时不能应用于高分辨领域,这个瓶颈急需突破.

[1]Snik F,Craven-Jones J,Escuti M,Fineschid S,Harringtone D,Martinof A D,Mawetg D,Riedih J,Tyo J S『2014Proc.SPIE 9099,Polarization:Measurement,Analysis,and Remote Sensing XIBaltimore,Maryland,United States,March 24–28,2014 p90990B』

[2]Tyo J,Goldstein L,Chenault B,Shaw A 2006Appl.Opt.45 5453

[3]Li S J,Jiang H L,Zhu J P,Duan J,Fu Q,Fu Y G,Dong K Y 2013Chin.Opt.6 803(in Chinese)[李淑军,姜会林,朱京平,段锦,付强,付跃刚,董科研 2013中国光学 6 803]

[4]Bass M,Mahajan N 2010Handbook of Optics,3rd Edition,Volume I:Geometrical and Physical Optics,Polarized Light,Components and Instruments(New York:McGraw Hill)pp478–512

[5]Wang Y,He H,Zeng N,Xie J,Liao R,Chang J,Sun M,Ma H 2015World J.Complex Med.1 74(in Chinese)[王晔,何宏辉,曾楠,谢军,廖然,常金涛,孙明皓,马辉 2015世界复合医学1 74]

[6]Goldstein D H 2010Polarized Light(3rd Ed.)(Boca Raton:CRC Press)pp628–631

[7]Lu S Y,Chipman R 1996J.Opt.Soc.Am.A13 1106

[8]Guo Y H 2014Ph.D.Dissertation(Shenzhen:Tsinghua University)pp10–30(in Chinese)[郭亦鸿2014博士学位论文 (深圳:清华大学)第11—30页]

[9]He H,Zeng N,Du E,Guo Y,Li D,Liao R,Ma H 2013Photon.Lasers Med.2 129

[10]Alali S,Vitkin A 2015J.Biomed.Opt.20 611041

[11]Pierangelo A,Nazac A,Benali A,Validire P,Cohen H,Novikova T,Ibrahim B,Manhas S,Fallet C,Antonelli M,Martino A 2013Opt.Express21 14120

[12]WangY,Kudenov M,KashaniA,KashaniA,Schwiegerling J,Escuti M『2015Proc.SPIE 9613,Polarization Science and Remote Sensing VIISan Diego,California,United States September 1,2015 p96130A』

[13]Bueno M,Artal P 1999Opt.Lett.24 64

[14]Li Y N,Sun X B,Qiao Y L,Zhang Q,Hong J 2010J.Atmos.Environ.Opt.5 203(in Chinese)[李雅男,孙晓兵,乔延利,张荞,洪津2010大气与环境光学学报5 203]

[15]Qiao L F,Zhang Y M,Xie Q Y,Fang J,Wang J J,Zhang Q X 2009J.Combust.Sci.Technol.15 172(in Chinese)[乔利锋,张永明,谢启源,方俊,王进军,张启兴2009燃烧科学与技术15 172]

[16]Wang Y,Wang H,Chen S,Qi Y,Liu H 2011Proc.SPIE 8192,International Symposium on Photoelectronic Detection and Imaging 2011 Laser Sensing and Imaging;and Biological and Medical Applications of Photonics Sensing and ImagingBeijing,China,August 23,2011 p81923U1

[17]Xiao S A,Li G H,Li J Z,Xue Q W 1991J.Qufu Normal Univ.18 44(in Chinese)[肖胜安,李国华,李继仲,薛庆文1991曲阜师范大学学报18 44]

[18]Wang X,Zhang M Y,Chen Z Y,Bai X F,Jin W Q 2013Infrared Laser Eng.42 2244(in Chinese)[王霞,张明阳,陈振跃,拜晓锋,金伟其2013红外与激光工程42 2244]

[19]Azzam A 1978Opt.Lett.2 148

[20]Collins W,Koh J 1999J.Opt.Soc.Am.A16 1997

[21]Gerligand Y,Smith M,Chipman R 1999Opt.Express4 420

[22]Laude-Boulesteix B,Martino A,Drévillon B,Schwartz L 2004Appl.Opt.43 2824

[23]Benkelfat E,Horache H,Zou Q,Vinouze B 2003Opt.Commun.221 271

[24]Jellison E,Modine A 1997Appl.Opt.36 8190

[25]Kudenov M,Escuti M,Hagen N,Dereniak E,Oka K 2012Opt.Lett.37 1367

[26]Goldstein D H 1992Appl.Opt.31 6676

[27]Pezzaniti L,Chipman R 1995Opt.Eng.34 1558

[28]Du E,He H,Zeng N,Sun M,Guo Y,Wu J,Ma H 2014J.Biomed.Opt.19 760131

[29]Sun M,He H,Zeng N,Du E,Guo Y,Liu S,Wu J,He R,Ma H 2014Biomed.Opt.Express5 4223

[30]Li J H,Zheng M,Zhang X B,Li Y Q 2016Laser Optoelectron.Prog.53 212021(in Chinese)[李建慧,郑猛,张雪冰,李艳秋2016激光与光电子学进展53 212021]

[31]Deng Y 2005Ph.D.Dissertation(Wuhan:Huazhong University of Science and Technology)pp83–97(in Chinese)[邓勇2005博士学位论文 (武汉:华中科技大学)第83–97页]

[32]Zhang X G,Jiang Y S,Lu X M 2008Acta Opt.Sin.28 1191(in Chinese)[张绪国,江月松,路小梅2008光学学报28 1191]

[33]Chen X G,Liu S Y,Zhang C W,Wu Y P,Ma Z C,Sun T Y,Xu Z M 2014Acta Phys.Sin.63 180701(in Chinese)[陈修国,刘世元,张传维,吴懿平,马智超,孙堂友,徐智谋2014物理学报63 180701]

[34]Li Y B,Li S B,Chen W J,Zeng Y X,Yang J Y 2010Opto-Electron.Eng.37 41(in Chinese)[李宇波,李世博,陈伟坚,曾宇骁,杨建义2010光电工程37 41]

[35]Kudenov M,Escuti M,Dereniak E Oka K 2011Appl.Opt.50 2283

[36]Oka K,Kaneko T 2003Opt.Express11 1510

[37]Luo H,Oka K,DeHoog E,Schiewgerling J,Dereniak E L 2008Appl.Opt.47 4413

[38]Luo H T 2008Ph.D.Dissertation(Arizona:Universityof Arizona)pp21–54

[39]Cao Q Z,Zhang C M,DeHoog E 2012Appl.Opt.51 5791

[40]Cao Q Z,Zhang J,DeHoog E,Zhang C M 2016Appl.Opt.55 954

[41]Cao Q Z,Zhang J,DeHoog E,Lu Y,Hu B Q,Li W G,Li J Y,Fan D X,Deng T,Yan Y 2016Acta Phys.Sin.65 050702(in Chinese)[曹奇志,张晶,Edward DeHoog,卢远,胡宝清,李武钢,李建映,樊东鑫,邓婷,阎妍2016物理学报65 050702]